基于模态凝聚算法的特征系统实现算法的自然激励技术研究（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/weixin_46039719/article/details/147709459

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

基于模态凝聚算法的特征系统实现算法的自然激励技术研究

一、自然激励技术（NExT）与特征系统实现算法（ERA）的基本原理

二、模态凝聚算法在NExT-ERA中的关键作用

三、关键技术难点与解决方案

四、应用场景与典型案例

五、现有改进方案与未来方向

六、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

自然激励技术（NExT）的基本原理和应用领域如下：

基本原理
自然激励技术（NExT）是一种利用环境中的自然激励（如风、波浪、交通等）作为输入，通过系统响应数据提取模态参数的方法。其核心思想是利用环境激励下的结构响应数据，通过计算互相关函数或脉冲响应函数来识别系统的模态参数。具体步骤包括：

选择参考点：选定一个响应较小的测点作为参考点。
计算互相关函数：计算其他测点与参考点的互相关函数。
模态参数识别：结合传统的模态参数识别方法，如特征系统实现算法（ERA），进行模态参数的提取。

NExT的优势在于其低成本、高效率和对结构干扰小的特点，适用于大型结构和复杂环境下的模态参数识别[1][2][3]。

应用领域

结构健康监测：NExT广泛应用于桥梁、高层建筑、风力涡轮机等大型结构的模态参数识别和健康监测。通过环境激励下的随机响应信号，可以快速准确地提取结构的模态频率、阻尼比和振型[1][3][4]。
机械系统：在机械系统中，NExT用于振动分析和故障诊断，特别是在复杂机械结构的模态参数识别中表现出色[1][2][3]。
电力系统：NExT在电力系统的机电振荡参数提取中也有应用，通过环境激励下的随机响应信号，可以实现电力系统的小干扰稳定在线评估[10][12][13]。
船舶结构：在船舶建造和维护过程中，NExT用于桥梁振动模态的识别，提供了一种无需人工激励的快速模态分析方法[15][23][24]。

未来发展方向

算法改进：继续优化NExT算法的鲁棒性和精度，特别是在非平稳环境和大型结构的应用中。
数据处理技术：持续改进数据预处理技术，提高模态参数提取的准确性和可靠性。
非线性系统应用：探索NExT在非线性系统中的应用，扩展其适用范围。
大型结构和复杂系统：进一步研究NExT在大型结构和复杂系统中的应用，提高其在实际工程中的实用性和有效性[1][2][3]。

综上所述，自然激励技术（NExT）是一种高效、低成本的模态参数识别方法，广泛应用于结构健康监测、机械系统分析、电力系统稳定评估和船舶结构振动分析等领域。未来的研究将进一步提升其在复杂环境和非线性系统中的应用能力。

模态凝聚算法的定义及其在信号处理中的作用

模态凝聚算法是一种用于信号处理的算法，其主要目的是通过将信号分解为多个子信号（模态）来提高信号处理的准确性和鲁棒性。模态（Mode）可以理解为原始信号中分解出的子信号，这些子信号通常具有特定的频率和振幅特征[35]。

在信号处理中，模态凝聚算法的作用主要体现在以下几个方面：

模态分离：模态凝聚算法能够将复杂的原始信号分解为多个独立的模态函数（IMF），每个模态函数代表信号中的一个特定频率或振幅成分。这种分离有助于更清晰地分析和处理信号[41][42]。
减少模态混叠：模态混叠是指同一个IMF分量中出现不同尺度或频率的信号，或者一个信号被分解为多个不同的IMF分量。模态凝聚算法通过优化算法设计，有效抑制模态混叠现象，从而提高信号处理的准确性[39][45]。
提高去噪效果：通过模态凝聚算法，可以更好地去除信号中的噪声成分。例如，集合经验模态分解（EEMD）通过引入白噪声，确保滤波器带宽的IMF作为基带，从而有效抑制噪声[45][58]。
增强信号特征提取：模态凝聚算法能够提取信号中的关键特征，如瞬时频率（IF）和瞬时振幅（IA），这些特征对于进一步的信号分析和分类非常重要[55][57]。
多模态融合：模态凝聚算法还可以与其他多模态融合技术结合使用，如深度学习模型，以实现更全面的信号处理和分析。例如，多模态融合技术可以通过特征级或决策级融合，将不同模态的数据表示进行有效整合，从而提高模型的预测精度和鲁棒性[36][44][52]。

综上所述，模态凝聚算法在信号处理中的作用主要体现在模态分离、减少模态混叠、提高去噪效果、增强信号特征提取以及多模态融合等方面。这些功能使得模态凝聚算法在各种信号处理应用中具有广泛的应用前景。

基于模态凝聚算法的特征系统实现算法的自然激励技术研究

一、自然激励技术（NExT）与特征系统实现算法（ERA）的基本原理

NExT的核心思想
自然激励技术（NExT）通过利用环境激励（如风、波浪、交通等）下结构的响应数据，计算不同测点之间的互相关函数，以替代传统模态分析中的脉冲响应函数。其数学基础在于两者的表达式具有一致性。例如，在电力系统中，NExT通过提取负荷随机波动引起的随机响应信号，结合动态模式分解（DMD）实现机电振荡参数的在线跟踪。
ERA的关键步骤
特征系统实现算法（ERA）是一种时域模态参数识别方法，通过构建Hankel矩阵并对其进行奇异值分解（SVD），提取系统的固有频率、阻尼比和模态振型。其核心优势在于高计算效率和稳定性，但对输入数据的信噪比和激励质量敏感。
NExT与ERA的结合逻辑
NExT提供环境激励下的互相关函数作为ERA的输入，替代传统人工激励下的脉冲响应数据。这种结合方式显著降低了测试成本，尤其适用于大型结构（如桥梁、风力涡轮机）的健康监测。

二、模态凝聚算法在NExT-ERA中的关键作用

模态凝聚算法的定义
模态凝聚算法（如变分模态分解VMD、经验模态分解EMD及其改进版本）通过将复杂信号分解为多个 固有模态函数（IMF） ，解决信号中的模态混叠问题。例如，VMD通过递归分解抑制端点效应和模态混叠，而EEMD通过添加白噪声改善分解效果。
在NExT-ERA中的具体应用
- 数据预处理：通过分解环境激励下的响应信号，提取与结构动态特性相关的自由衰减分量，减少噪声和非线性干扰。
- 模态参数优化：在电力系统中，NExT-DMD结合动态模式分解，显著提升了振荡频率和阻尼比的提取精度。
- 非线性系统处理：针对风力涡轮机等非线性系统，改进的EMD（IEMD）通过抑制模态混叠，提升互相关函数的质量。

三、关键技术难点与解决方案

数据质量与激励非平稳性
- 难点：自然激励的随机性和低能量特性可能导致信噪比不足，影响ERA的精度。
- 解决方案：采用小波变换、中值滤波等信号处理技术，优化数据预处理流程。
Hankel矩阵参数选择
- 难点：Hankel矩阵的维数（行延迟、列延迟）直接影响模态识别的准确性。
- 优化建议：分析数据长度需大于第一阶自振周期的60倍，Hankel矩阵维数可通过经验公式确定。
模态混叠与虚假模态
- 难点：密集模态或高阻尼结构的识别中易出现模态混叠。
- 改进方法：采用集成EMD（EEMD）或变分模态分解（VMD），结合稳定性图筛选虚假模态。

四、应用场景与典型案例

结构健康监测
- 案例：在悬索桥模型和输电塔中，NExT-ERA成功提取高精度模态参数，验证了其在复杂结构中的有效性。
- 优势：无需人工激励，适用于桥梁、高层建筑等难以施加激励的场景。
机械故障诊断
- 案例：结合改进EMD（IEMD）与NExT，减少模态交叉干扰，提升齿轮箱和轴承的故障检测灵敏度。
风力涡轮机分析
- 案例：通过风洞实验验证NExT在风力涡轮机模态分析中的可行性，发现高频下的频率偏差主要由估计误差引起。
- 挑战：旋转叶片的气动耦合效应需进一步结合非线性模态分解算法。

五、现有改进方案与未来方向

算法改进案例
- NExT-IEMD：Yang等人将改进经验模态分解与NExT结合，抑制多阶模态间的相互干扰，提升参数识别精度。
- NExT-SSI：通过协方差计算保留原始数据信息，结合随机子空间法（SSI）缩短计算时间并提高鲁棒性。
未来研究方向
- 非线性系统扩展：开发适用于风力涡轮机叶片等非线性结构的模态凝聚算法。
- 多传感器融合：结合多源数据（如振动、应变、声发射）提升模态参数提取的全面性。
- 实时性与边缘计算：优化算法计算效率，支持在线监测与实时反馈。

六、结论

NExT-ERA方法通过结合自然激励的低成本优势和ERA的高效性，在结构健康监测与机械故障诊断中展现出广泛的应用前景。模态凝聚算法的引入进一步解决了环境激励下的信噪比和模态混叠问题。未来研究需在非线性系统适应性、算法鲁棒性及实时性方面持续突破，以满足工程实践中日益复杂的动态特性分析需求。

📚2 运行结果

部分代码：

%Apply modal superposition to get response
%--------------------------------------------------------------------------

n=size(f,1);
dt=1/fs; %sampling rate
[Vectors, Values]=eig(K,M);
Freq=sqrt(diag(Values))/(2*pi); % undamped natural frequency
steps=size(f,2);

Mn=diag(Vectors'*M*Vectors); % uncoupled mass
Cn=diag(Vectors'*C*Vectors); % uncoupled damping
Kn=diag(Vectors'*K*Vectors); % uncoupled stifness
wn=sqrt(diag(Values));
zeta=Cn./(sqrt(2.*Mn.*Kn)); % damping ratio
wd=wn.*sqrt(1-zeta.^2);

fn=Vectors'*f; % generalized input force matrix

t=[0:dt:dt*steps-dt];

for i=1:1:n

h(i,:)=(1/(Mn(i)*wd(i))).*exp(-zeta(i)*wn(i)*t).*sin(wd(i)*t); %transfer function of displacement
hd(i,:)=(1/(Mn(i)*wd(i))).*(-zeta(i).*wn(i).*exp(-zeta(i)*wn(i)*t).*sin(wd(i)*t)+wd(i).*exp(-zeta(i)*wn(i)*t).*cos(wd(i)*t)); %transfer function of velocity
hdd(i,:)=(1/(Mn(i)*wd(i))).*((zeta(i).*wn(i))^2.*exp(-zeta(i)*wn(i)*t).*sin(wd(i)*t)-zeta(i).*wn(i).*wd(i).*exp(-zeta(i)*wn(i)*t).*cos(wd(i)*t)-wd(i).*((zeta(i).*wn(i)).*exp(-zeta(i)*wn(i)*t).*cos(wd(i)*t))-wd(i)^2.*exp(-zeta(i)*wn(i)*t).*sin(wd(i)*t)); %transfer function of acceleration

qq=conv(fn(i,:),h(i,:))*dt;
qqd=conv(fn(i,:),hd(i,:))*dt;
qqdd=conv(fn(i,:),hdd(i,:))*dt;

q(i,:)=qq(1:steps); % modal displacement
qd(i,:)=qqd(1:steps); % modal velocity
qdd(i,:)=qqdd(1:steps); % modal acceleration

end

x=Vectors*q; %displacement
v=Vectors*qd; %vecloity
a=Vectors*qdd; %vecloity

%Add noise to excitation and response
%--------------------------------------------------------------------------
f2=f+0.1*randn(2,10000);
a2=a+0.1*randn(2,10000);
v2=v+0.1*randn(2,10000);
x2=x+0.1*randn(2,10000);

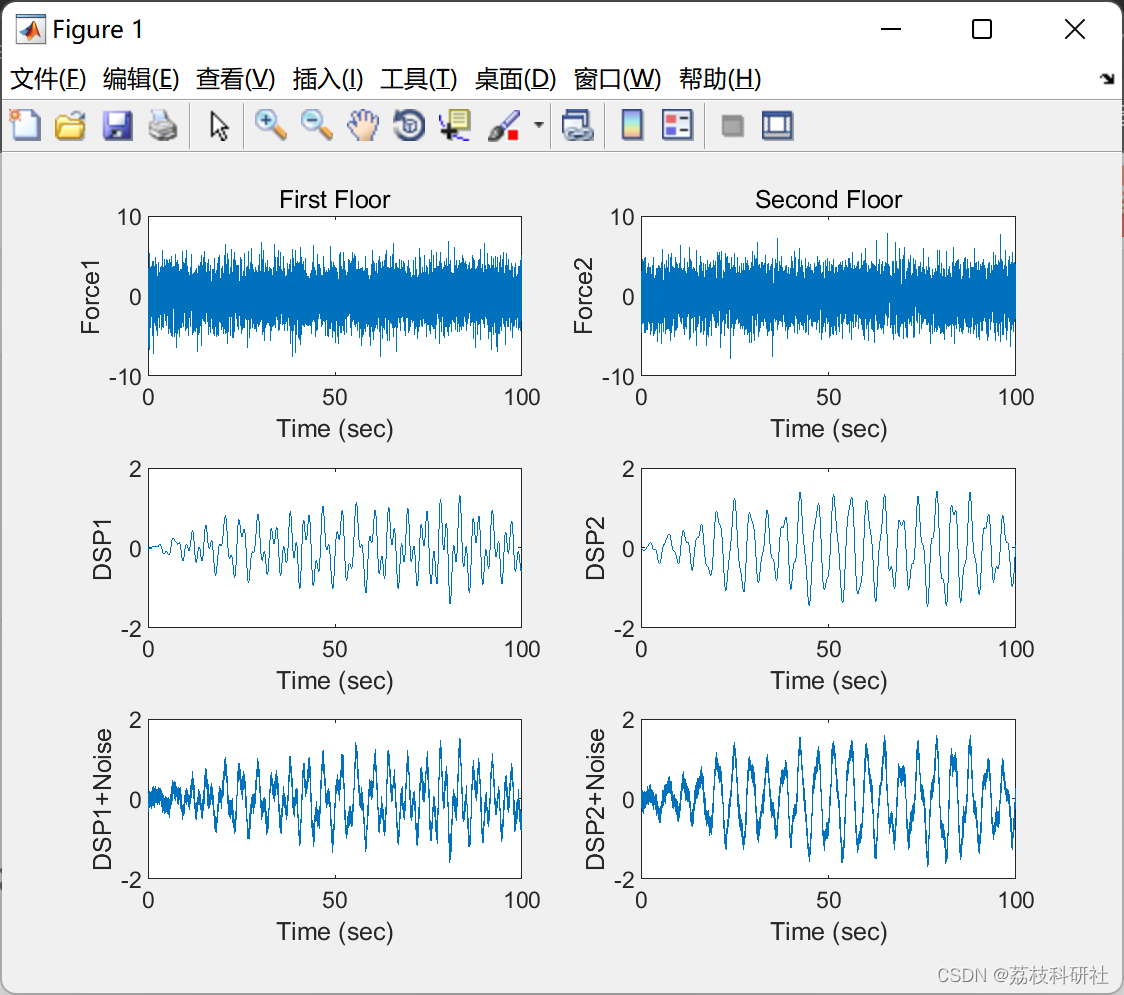
%Plot displacement of first floor without and with noise
%--------------------------------------------------------------------------
figure;
subplot(3,2,1)
plot(t,f(1,:)); xlabel('Time (sec)'); ylabel('Force1'); title('First Floor');
subplot(3,2,2)
plot(t,f(2,:)); xlabel('Time (sec)'); ylabel('Force2'); title('Second Floor');
subplot(3,2,3)
plot(t,x(1,:)); xlabel('Time (sec)'); ylabel('DSP1');
subplot(3,2,4)
plot(t,x(2,:)); xlabel('Time (sec)'); ylabel('DSP2');
subplot(3,2,5)
plot(t,x2(1,:)); xlabel('Time (sec)'); ylabel('DSP1+Noise');
subplot(3,2,6)
plot(t,x2(2,:)); xlabel('Time (sec)'); ylabel('DSP2+Noise');

%Identify modal parameters using displacement with added uncertainty
%--------------------------------------------------------------------------
data=x2;
refch=2;
maxlags=999;
window=2000;
N=5;
p=0;
ncols=800;
nrows=200;
cut=4;
shift=10;
EMAC_option=1;

[Result1] = NExTFERA(data,refch,window,N,p,fs,ncols,nrows,cut,shift,EMAC_option);
[Result2] = NExTTERA(data,refch,maxlags,fs,ncols,nrows,cut,shift,EMAC_option);

%Plot Impulse Response Functions
%--------------------------------------------------------------------------
IRFT= NExTT(data,refch,maxlags);
IRFF= NExTF(data,refch,window,N,p);

t2=[0:dt:999*dt];
figure;
subplot(2,2,1)
plot(t2,IRFT(1,:)); xlabel('Time (sec)'); ylabel('IRF1'); title('NExTT');
subplot(2,2,2)
plot(t2,IRFF(1,:)); xlabel('Time (sec)'); ylabel('IRF1'); title('NExTF');
subplot(2,2,3)
plot(t2,IRFT(2,:)); xlabel('Time (sec)'); ylabel('IRF2');
subplot(2,2,4)
plot(t2,IRFF(2,:)); xlabel('Time (sec)'); ylabel('IRF2');

%Plot real and identified first modes to compare between them
%--------------------------------------------------------------------------
figure;
plot([0 ; -Vectors(:,1)],[0 1 2],'r*-');
hold on
plot([0 ;Result1.Parameters.ModeShape(:,1)],[0 1 2],'go-.');
hold on
plot([0 ;Result2.Parameters.ModeShape(:,1)],[0 1 2],'y^--');
hold on
plot([0 ; -Vectors(:,2)],[0 1 2],'b^-');
hold on
plot([0 ;Result1.Parameters.ModeShape(:,2)],[0 1 2],'mv-.');
hold on
plot([0 ;Result2.Parameters.ModeShape(:,2)],[0 1 2],'co--');
hold off
title('Real and Identified Mode Shapes');
legend('Mode 1 (Real)','Mode 1 (Identified using NExTF-ERA)','Mode 1 (Identified using NExTT-ERA)'...
,'Mode 2 (Real)','Mode 2 (Identified using NExTF-ERA)','Mode 2 (Identified using NExTT-ERA)');
xlabel('Amplitude');
ylabel('Floor');
grid on;
daspect([1 1 1]);

%Display real and Identified natural frequencies and damping ratios
%--------------------------------------------------------------------------
disp('Real and Identified Natural Drequencies and Damping Ratios of the First Mode');
disp(strcat('Real: Frequency=',num2str(Freq(1)),'Hz',' Damping Ratio=',num2str(zeta(1)*100),'%'));
disp(strcat('NExTF-ERA: Frequency=',num2str(Result1.Parameters.NaFreq(1)),'Hz',' Damping Ratio=',num2str(Result1.Parameters.DampRatio(1)),'%'));
disp(strcat('CMI of The Identified Mode=',num2str(Result1.Indicators.CMI(1)),'%'));
disp(strcat('NExTT-ERA: Frequency=',num2str(Result2.Parameters.NaFreq(1)),'Hz',' Damping Ratio=',num2str(Result2.Parameters.DampRatio(1)),'%'));
disp(strcat('CMI of The Identified Mode=',num2str(Result2.Indicators.CMI(1)),'%'));
disp('-----------')