💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
用于电源转换器和驱动器的长期预测范围FCS-MPC研究
摘要:有限控制集模型预测控制(FCS-MPC)是功率转换系统的一种突出控制方法,最近非常受欢迎。一些研究强调了长预测范围在闭环稳定性、谐波失真和开关损耗方面实现的性能优势。然而,由于其固有的高计算负担,实际实现并不简单。为了克服这一障碍,可以将控制问题表述为整数最小二乘优化问题,相当于格中的最近点搜索或最近向量问题。文献中提出了不同的技术来解决它,其中球体解码算法(SDA)是解决长预测视界FCS-MPC的最流行选择。然而,该领域的最新技术提供了超越传统SDA的解决方案,本文将介绍这些解决方案以及该主题的未来趋势和挑战。
要定义FCS-MPC策略,需要三个基本要素:预测模型,成本函数和优化算法。预测模型计算系统状态变量在未来时间步长的演变,给定初始状态和可通过预测范围应用的可能控制输入序列。成本函数根据控制目标评估每个可能的轨迹和控制输入的适用性。优化算法最小化目标函数并选择控制输入的最佳顺序。
一、FCS-MPC的技术背景与核心原理
有限控制集模型预测控制(FCS-MPC)是一种基于离散系统特性的控制方法,通过枚举所有可能的开关状态并选择成本函数最小的最优电压矢量作为控制输出。其核心原理包括以下特征:
- 离散特性与无调制需求:FCS-MPC直接利用电力电子器件的离散开关状态(如逆变器的7种电压矢量),无需脉宽调制(PWM),简化了控制结构。
- 多目标优化能力:通过设计包含多个控制目标(如电流跟踪、功率调节、开关损耗)的成本函数,FCS-MPC可同时处理非线性约束和优先级目标。
- 动态响应优势:与传统PI控制相比,FCS-MPC的滚动优化机制使其在动态负载变化(如电机加速、电网扰动)中具有更快的响应速度。
二、电源转换器与驱动器的控制需求及FCS-MPC的适配性
电源转换器和驱动器面临的核心需求包括:高效率、高功率密度、动态性能、EMI抑制以及多目标协同控制。FCS-MPC的适配性体现在以下方面:
- 动态性能优化:在电机驱动中,FCS-MPC可通过直接控制转矩和磁链(MPTC)实现快速转矩响应,例如在永磁同步电机(PMSM)中,其动态性能比传统磁场定向控制(FOC)快30%以上。
- 复杂约束处理:在微电网和可再生能源系统中,FCS-MPC可同时处理并网电流谐波抑制、功率因数调节和直流母线电压稳定等多重约束。
- 无传感器控制潜力:通过结合预测模型与观测器(如滑模观测器),FCS-MPC可减少对物理传感器的依赖,降低系统成本。
三、长期预测范围(LPH)对FCS-MPC的影响机制
长期预测范围(LPH,Long Prediction Horizon)通过扩展预测步长(通常超过10步)优化系统性能,但也带来新的挑战:
- 性能提升:
- 稳定性增强:长预测范围可捕捉系统动态的长期行为,减少稳态误差和谐波失真。例如,在三相PWM整流器中,LPH-FCS-MPC可将电流THD从5.45%降至3.16%。
- 开关损耗优化:多步预测允许提前规划开关状态序列,降低平均开关频率。实验表明,采用两步预测的FCS-MPC可将开关损耗减少15%-20%。
- 技术挑战:
- 计算复杂度:预测步长增加导致候选开关状态数呈指数增长。例如,两电平逆变器的候选状态数随步长NN按7N7N增长,需依赖球体解码算法(SDA)等优化方法降低计算量。
- 权重因子调整:长预测范围需在多目标成本函数中平衡不同物理量(如转矩与磁链)的权重系数,传统试错法效率低,需建立基于稳定性分析的权重规则。
四、FCS-MPC在电力电子领域的应用现状与最新进展
- 典型应用场景:
- 电机驱动:在PMSM和感应电机(IM)中,FCS-MPC通过MPTC和MPCC实现高精度转矩控制,尤其在电动汽车驱动中表现出快速响应(<1ms)和低电流纹波。
- 可再生能源系统:在光伏并网逆变器中,FCS-MPC用于有功/无功功率调节和谐波抑制,支持低电压穿越(LVRT)等电网规范要求。
- 微电网储能:通过双向DC/DC转换器控制电池充放电,FCS-MPC在动态负载变化下实现效率提升(较PI控制提高5%-8%)。
- 改进方向:
- 计算效率优化:采用并行处理(FPGA实现)和分层预测策略,例如在矩阵变换器中,简化FCS-MPC算法可减少50%的计算时间。
- 混合控制架构:结合FCS-MPC与传统控制(如PI、滑模控制)构建切换策略,兼顾稳态精度与动态性能。
- 数据驱动增强:引入机器学习算法在线调整模型参数,降低对精确数学模型的依赖,提升鲁棒性。
五、实验验证与性能对比
- 动态性能验证:
- 在PMSM控制中,改进的FCS-MPC(结合扰动补偿)相比传统方法,三相电流波动降低40%,转矩响应时间缩短至0.2秒。

- 在电阻参数突变(2倍变化)时,传统FCS-MPC导致直流侧电压振荡±85V,而改进策略(虚拟矢量优选)保持电压稳定。
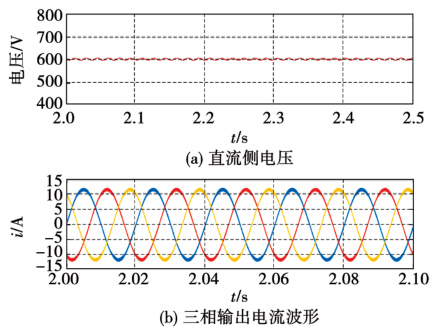
- 在PMSM控制中,改进的FCS-MPC(结合扰动补偿)相比传统方法,三相电流波动降低40%,转矩响应时间缩短至0.2秒。
- 效率与损耗对比:
- 三电平NPC整流器中,预测直接功率控制(P-DPC)策略将开关损耗降低20%,同时维持无功功率波动低于1%。
- 在储能系统DC/DC转换器中,FCS-MPC相比PI控制,效率提升至98.5%,且动态负载切换时的电压波动减少50%。
六、未来研究方向与挑战
- 理论完善:
- 稳定性分析:建立基于李雅普诺夫函数的稳定性判据,解决长预测范围下的闭环稳定性证明问题。
- 标准化权重规则:通过频域分析或灵敏度方法,推导权重因子与系统性能的定量关系。
- 技术融合:
- 宽禁带器件适配:针对SiC/GaN器件的高频特性,优化FCS-MPC的开关频率和EMI性能。
- 边缘计算集成:利用边缘计算平台实现分布式预测控制,支持多转换器协同(如微电网集群)。
- 工业落地挑战:
- 确定性开关频率:开发定频FCS-MPC算法,满足工业标准(如IEEE 1547对并网逆变器的谐波要求)。
- 硬件加速方案:基于FPGA或专用ASIC芯片实现实时计算,将预测步长扩展至20步以上。
七、总结
长期预测范围FCS-MPC在电源转换器和驱动器中展现出显著优势,但其广泛应用仍需解决计算效率、权重因子优化和硬件实现等关键问题。未来研究应聚焦于理论深化与技术创新,推动FCS-MPC在新能源、电动汽车和智能电网等领域的规模化应用。
📚2 运行结果


主函数代码:
clear all
clc
%% Original FCS
% \V = \{ u_{\min},...,u_{\max} \} \subset \Z
u_min=0; %Minimum value for input
u_max=1; %Maximum value for input
%% Multistep FCS
% u \in \V^n_u \subset \Z^n_u
% \U_k = \V^n_u Np \subset \Z^p; p=n_u Np
n_u = 3; % Number of inputs u=[Sa Sb Sc]'
Np = 7; % Prediction Horizon length
p = n_u*Np; % Length of switching sequences U_k
Kbest = 8; % Kb parameter for K-best SDA
Niter_max = 32000; % Maximum number of explored nodes for SDA
%% Basic Matrices
I_2 = eye(2); % Identity matrices
I_3 = eye(3);
O_2 = zeros(2); % Zero matrices
J = [0 -1;
1 0];
Tr = sqrt(2/3)*[1 -0.5 -0.5; % Clarke transform
0 sqrt(3)/2 -sqrt(3)/2];
%% Continuous-Time alpha-beta Model -> 2 lvl VSI with output LC filter as example
n_y = 2; % Number of outputs for control y= [vo_alpha vo_beta]
Ts = 50e-6; % Sample Time
Lf = 0.002; % LC filter inductor
Cf = 50e-6; % LC filter capacitor
w = 2*pi*50; % Angular frequency (@50 Hz)
Vdc = 400; % Dc link voltage
Vo_ref_amp = 110; % Output voltage amplitude reference
lambda = 60.0; % Weighting factor: Switching effort penalty
Rr=[1 -w*Ts; % Rotation matrix
w*Ts 1];
Ac_xy = [O_2 -(1/Lf)*I_2 O_2 ;
(1/Cf)*I_2 O_2 -(1/Cf)*I_2 ;
O_2 O_2 w*J ;];
Bc_xy = [(Vdc/Lf)*I_2 O_2 O_2]'*Tr ;
Cxy = [I_2 O_2 O_2;
O_2 I_2 O_2]; % C for observer
ct_sys = ss(Ac_xy,Bc_xy,Cxy,[]);
%% Discrete-Time alpha-beta Model
dt_sys = c2d(ct_sys,Ts);
A = dt_sys.a;
B = dt_sys.b;
%% Multistep Matrices (H is lower triangular)
C = zeros(n_y,6); % C for control, 2 rows because only voltage is controlled
C(1:n_y,3:4) = eye(2);
[UpsilonT,Gamma,lSTE,W_inv,H] = MPC_Matrices_l(A,B,C,Np,lambda); %Multistep matrices
%% Initialize variables
Uop_ESA = zeros(p,1);
Uop_SDA = zeros(p,1);
Uop_Kbest = zeros(p,1);
F_k=zeros(p,1);
Niter=0.0; % Count nodes
Niter_ac=0.0;
Niter_avg=0.0;
sim = 0; % Number of simulations
simMAX = 1;
uabc_k_1 = [0 0 0]'; % Assume previous state is 0 0 0
while (sim < simMAX)
%% Vo Reference
theta = 2*pi*(rand(1)); % Syncronization angle, generated randomly in this example
Vo_abc_ref = Vo_ref_amp*[sin(theta); sin(theta-2*pi/3); sin(theta+2*pi/3)];
Vo_xy_ref = Tr*Vo_abc_ref; % Vo reference in alpha-beta
%% Output sequences
Yref=zeros(n_y*Np,1);
Yref(1:2,1)=Rr*Vo_xy_ref; % Construct output reference sequence
for k=n_y+1:n_y:n_y*Np
row_i=k;
row_f=k+n_y-1;
Yref(row_i:row_f,:)=Rr*Yref(row_i-n_y:row_f-n_y,:);
end
%% System state
Vo_xy = Vo_xy_ref + 20*(rand(1)-0.5); % Assume Vo around reference with +-10 V error
Io_xy = [0 0]'; % Assume output current is zero
Ii_xy = Io_xy + (Cf/Ts)*(Rr*Vo_xy-Vo_xy); % Approximate filter current
x_k = [Ii_xy ; Vo_xy; Io_xy]; % System state variables
%% Unconstrained solution calculation
F_k=UpsilonT*(Gamma*x_k-Yref)-lSTE*uabc_k_1;
U_unc=-W_inv*F_k;
%U_unc = 4*(rand(p,1)-0.5); % To generate randomly
%U_unc = min(u_max+1, max(u_min-1, U_unc)); % Limit unconstrained values
U_bar_unc = H*U_unc; % Center of the sphere in the transformed space
%% Initial Vector U_ini -> Only for SDA
U_ini = zeros(p,1); % Null vector
%U_vec_ini=round(U_vec_unc); % Babai
% for k =1 : p
% if (U_vec_ini(k,1)<u_min)
% U_vec_ini(k,1)=u_min;
% end
% if (U_vec_ini(k,1)>u_max)
% U_vec_ini(k,1)=u_max;
% end
% end
%% Exhaustive Search Algorithm
Uop_ESA = ESA(U_bar_unc, H, u_min, u_max, p);
%% Sphere Decoding Algorithm
[Uop_SDA,Niter,Rs2] = SDA_l(U_bar_unc, H, u_min, u_max, p, U_ini,Niter_max);
%% K-best Sphere Decoding Algorithm
[Uop_Kbest,NiterKb,Rs2Kb] = SDAKbestl(U_bar_unc, H, u_min, u_max, p,Kbest);
Uop_ESA'
Uop_SDA'
Niter
Uop_Kbest'
NiterKb
Niter_ac=Niter_ac+Niter;
sim = sim+1;
end
Niter_avg=Niter_ac/sim;clear all
clc
%% Original FCS
% \V = \{ u_{\min},...,u_{\max} \} \subset \Z
u_min=0; %Minimum value for input
u_max=1; %Maximum value for input
%% Multistep FCS
% u \in \V^n_u \subset \Z^n_u
% \U_k = \V^n_u Np \subset \Z^p; p=n_u Np
n_u = 3; % Number of inputs u=[Sa Sb Sc]'
Np = 7; % Prediction Horizon length
p = n_u*Np; % Length of switching sequences U_k
Kbest = 8; % Kb parameter for K-best SDA
Niter_max = 32000; % Maximum number of explored nodes for SDA
%% Basic Matrices
I_2 = eye(2); % Identity matrices
I_3 = eye(3);
O_2 = zeros(2); % Zero matrices
J = [0 -1;
1 0];
Tr = sqrt(2/3)*[1 -0.5 -0.5; % Clarke transform
0 sqrt(3)/2 -sqrt(3)/2];
%% Continuous-Time alpha-beta Model -> 2 lvl VSI with output LC filter as example
n_y = 2; % Number of outputs for control y= [vo_alpha vo_beta]
Ts = 50e-6; % Sample Time
Lf = 0.002; % LC filter inductor
Cf = 50e-6; % LC filter capacitor
w = 2*pi*50; % Angular frequency (@50 Hz)
Vdc = 400; % Dc link voltage
Vo_ref_amp = 110; % Output voltage amplitude reference
lambda = 60.0; % Weighting factor: Switching effort penalty
Rr=[1 -w*Ts; % Rotation matrix
w*Ts 1];
Ac_xy = [O_2 -(1/Lf)*I_2 O_2 ;
(1/Cf)*I_2 O_2 -(1/Cf)*I_2 ;
O_2 O_2 w*J ;];
Bc_xy = [(Vdc/Lf)*I_2 O_2 O_2]'*Tr ;
Cxy = [I_2 O_2 O_2;
O_2 I_2 O_2]; % C for observer
ct_sys = ss(Ac_xy,Bc_xy,Cxy,[]);
%% Discrete-Time alpha-beta Model
dt_sys = c2d(ct_sys,Ts);
A = dt_sys.a;
B = dt_sys.b;
%% Multistep Matrices (H is lower triangular)
C = zeros(n_y,6); % C for control, 2 rows because only voltage is controlled
C(1:n_y,3:4) = eye(2);
[UpsilonT,Gamma,lSTE,W_inv,H] = MPC_Matrices_l(A,B,C,Np,lambda); %Multistep matrices
%% Initialize variables
Uop_ESA = zeros(p,1);
Uop_SDA = zeros(p,1);
Uop_Kbest = zeros(p,1);
F_k=zeros(p,1);
Niter=0.0; % Count nodes
Niter_ac=0.0;
Niter_avg=0.0;
sim = 0; % Number of simulations
simMAX = 1;
uabc_k_1 = [0 0 0]'; % Assume previous state is 0 0 0
while (sim < simMAX)
%% Vo Reference
theta = 2*pi*(rand(1)); % Syncronization angle, generated randomly in this example
Vo_abc_ref = Vo_ref_amp*[sin(theta); sin(theta-2*pi/3); sin(theta+2*pi/3)];
Vo_xy_ref = Tr*Vo_abc_ref; % Vo reference in alpha-beta
%% Output sequences
Yref=zeros(n_y*Np,1);
Yref(1:2,1)=Rr*Vo_xy_ref; % Construct output reference sequence
for k=n_y+1:n_y:n_y*Np
row_i=k;
row_f=k+n_y-1;
Yref(row_i:row_f,:)=Rr*Yref(row_i-n_y:row_f-n_y,:);
end
%% System state
Vo_xy = Vo_xy_ref + 20*(rand(1)-0.5); % Assume Vo around reference with +-10 V error
Io_xy = [0 0]'; % Assume output current is zero
Ii_xy = Io_xy + (Cf/Ts)*(Rr*Vo_xy-Vo_xy); % Approximate filter current
x_k = [Ii_xy ; Vo_xy; Io_xy]; % System state variables
%% Unconstrained solution calculation
F_k=UpsilonT*(Gamma*x_k-Yref)-lSTE*uabc_k_1;
U_unc=-W_inv*F_k;
%U_unc = 4*(rand(p,1)-0.5); % To generate randomly
%U_unc = min(u_max+1, max(u_min-1, U_unc)); % Limit unconstrained values
U_bar_unc = H*U_unc; % Center of the sphere in the transformed space
%% Initial Vector U_ini -> Only for SDA
U_ini = zeros(p,1); % Null vector
%U_vec_ini=round(U_vec_unc); % Babai
% for k =1 : p
% if (U_vec_ini(k,1)<u_min)
% U_vec_ini(k,1)=u_min;
% end
% if (U_vec_ini(k,1)>u_max)
% U_vec_ini(k,1)=u_max;
% end
% end
%% Exhaustive Search Algorithm
Uop_ESA = ESA(U_bar_unc, H, u_min, u_max, p);
%% Sphere Decoding Algorithm
[Uop_SDA,Niter,Rs2] = SDA_l(U_bar_unc, H, u_min, u_max, p, U_ini,Niter_max);
%% K-best Sphere Decoding Algorithm
[Uop_Kbest,NiterKb,Rs2Kb] = SDAKbestl(U_bar_unc, H, u_min, u_max, p,Kbest);
Uop_ESA'
Uop_SDA'
Niter
Uop_Kbest'
NiterKb
Niter_ac=Niter_ac+Niter;
sim = sim+1;
end
Niter_avg=Niter_ac/sim;
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(内容仅供参考,具体以第2部分运行结果为准。)
[1]朱厚达,陈才学,刘凯,等.级联多电平逆变器有限控制集模型预测控制[J].计算技术与自动化, 2018, 37(2):6.
[2]常峰,雷雁雄,刘源俊,等.改进型有限集模型预测控制在三相电压型PWM整流器中的应用[J].科技广场, 2017(7):10.
[3]王洋,程志江,李永东.三电平并网变换器的模型预测控制[J].电力系统及其自动化学报, 2018, 30(10):8.

























 2800
2800

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










