《Pytorch深度学习实践》P6 逻辑斯蒂回归（Logistic Regression） 代码+笔记：Sigmoid函数（Logistic等）、交叉熵损失（BCE）

最新推荐文章于 2025-05-19 04:15:00 发布
原创 最新推荐文章于 2025-05-19 04:15:00 发布 · 1.2k 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#深度学习 #pytorch #回归 #机器学习 #分类

b站的up主刘二大人的《PyTorch深度学习实践》P6 笔记+代码，视频链接。

目录

一、Sigmoid函数

1、Logistic函数（最常用Sigmoid函数）

2、 Tanh函数

3、Softsign 函数

4、Arctan 函数

二、交叉熵损失

1、二分类的交叉熵损失（Binary Cross-Entropy，简称 BCE）：

2、多分类的交叉熵损失公式：

三、代码+图像+流程

一、Sigmoid函数

介绍：Sigmoid函数是一类S形的非线性激活函数，饱和型函数。下面介绍几种函数：Logistic函数、Tanh函数、Softsign 函数、Arctan 函数。在无特殊说明的时候，Sigmoid函数默认为Logistic函数。

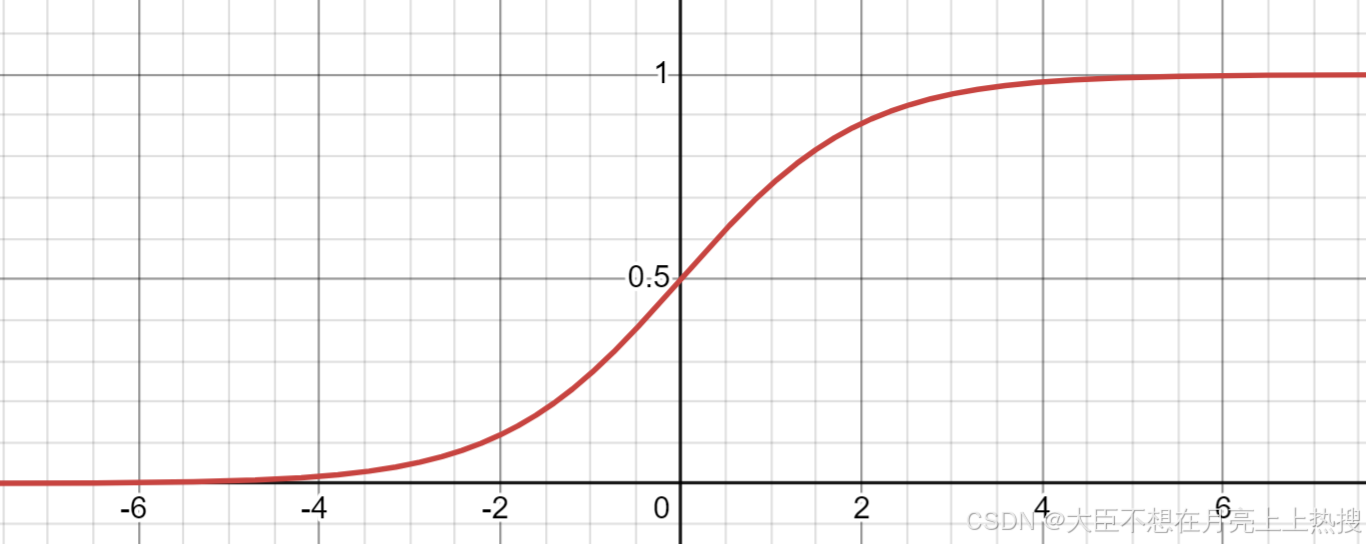
1、Logistic函数（最常用Sigmoid函数）

公式：f(x) = \frac{1}{1 + e^{-x}}

特性：输出范围为[0,1],适合处理二分类问题，表示概率值。

函数图像：

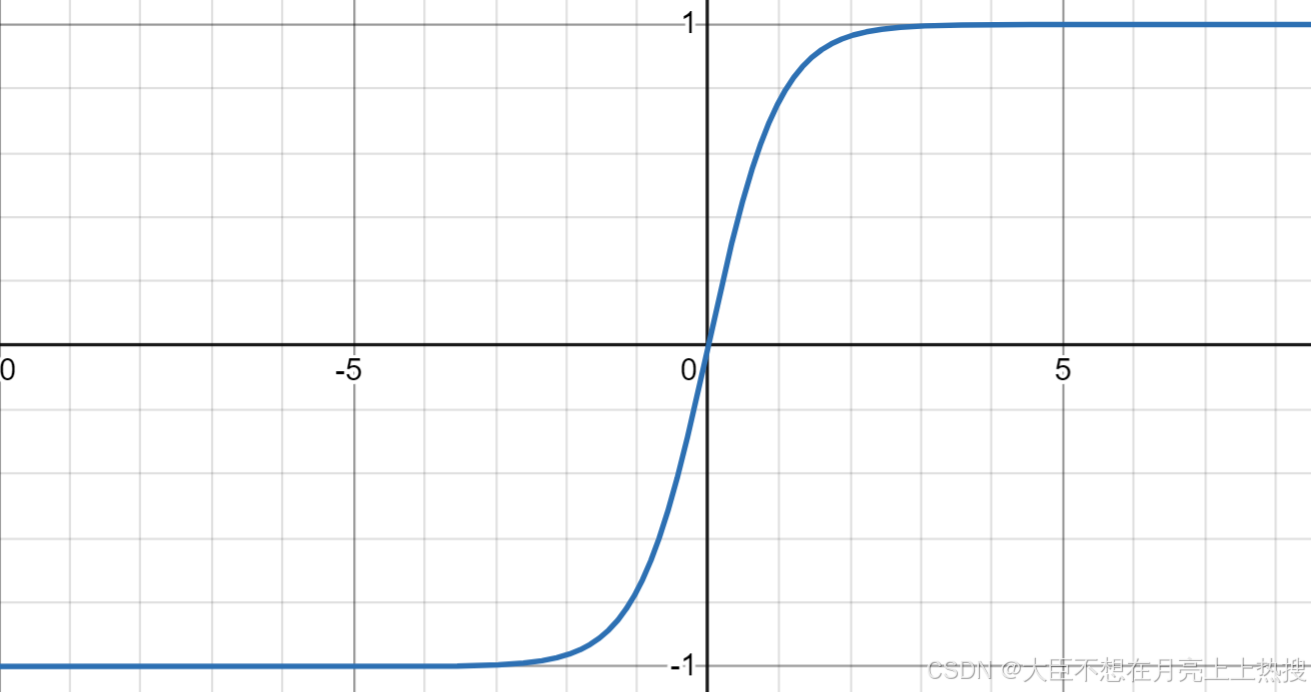
2、 Tanh函数

公式：f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

特性：输出范围为[-1,1],适用于处理输入值可以是正、负的情形。

函数图像：

3、Softsign 函数

公式：f(x) = \frac{x}{1 + |x|}

特性：输出范围为(-1, 1)。Softsign在趋近于极值时变化较慢，比Tanh更平滑。

函数图像：

最低0.47元/天 解锁文章
常见激活函数（sigmoid/logistic/tanh/softmax/ReLU关系解释）
Irene_Loong的博客
09-16 8257
常见激活函数sigmoid、logistic、tanh、softmax、ReLU简介及关系解释。
Logistic回归与Sigmoid函数
qq_43255766的博客
10-28 3900
一、Logistic回归： 1.1 特征： Logistic回归主要是二分类预测 ，是对概率的估计的一种方法。概率的取值范围在（0，1）。当P>0.5时，预测为1；当P>0.5时，预测为0。(这也就和下文的Sigmoid 函数一样)。 1.2 分类： Logistic回归属于广义线性模型，利用Logistic回归进行分类的主要思想是：根据现有的数据对分类便捷线建立回归。 1.3 ...
Sigmoid 函数(logistic函数)笔记
热门推荐
西之可乐的专栏
07-19 5万+
其实logistic函数也就是经常说的sigmoid函数，它的几何形状也就是一条sigmoid曲线（S型曲线）。   该函数具有如下的特性：当x趋近于负无穷时，y趋近于0；当x趋近于正无穷时，y趋近于1；当x= 0时，y=0.5.   优点： 1.Sigmoid函数的输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可以用作输出层。 2.求导容易。 缺点： 1.由...
机器学习：Logstic回归函数和Sigmoid函数
最新发布
dami10124的博客
05-19 1127
逻辑回归虽然名称中有"回归"二字，但实际上是一种广泛使用的分类算法，特别适合处理二分类问题。它的核心思想是通过线性回归的组合加上Sigmoid函数，将输出映射到(0,1)区间，表示属于某一类的概率。逻辑回归作为机器学习中最基础的分类算法之一，理解其数学原理和实现细节对学习更复杂的模型至关重要。从数学推导到Python实现，展示了逻辑回归的各个方面：Sigmoid函数的数学性质及其在分类中的作用极大似然估计与交叉熵损失的推导梯度下降算法的具体实现各种改进和扩展方法。
【机器学习】【逻辑回归】Logistic函数/Sigmoid函数的详细公式推导
蔚蓝的天空Tom
03-19 3万+
sigmoid函数的数学公式                sigmoid函数的因变量x取值范围是-∞到+∞，(-∞，+∞)，但是sigmoid函数的值域是(0, 1)。不管x取什么值其对应的sigmoid函数值一定会落到(0,1)范围内~~~漂亮的logistic 曲线sigmoid函数对应的图形就是logistic曲线，logistic曲线对应的函数就是sigmoid函数。下面我们用通过spy...
PyTorch深度学习实践——Logistic Regression
m0_60458471的博客
09-01 811
在本次学习中，学习到了大名鼎鼎的logistic回归，虽然说是一种回归模型，但是这个模型实际上是做分类问题，对于这种回归模型我们同样从三个方面来进行介绍，logistic回归是什么？为什么要采用logistics回归？如何实现losgistic回归模型？下面是对于logistic回归的总结： logistic回归是什么？ 为什么要采用logistics回归？ 在解释为什么需要采用logistics回归之前，我们先对分类与回归任务进行比较 在之前实现的线性回归模型中...
Pytorch实现logistic回归（算法+代码）
qq_35328355的博客
07-12 2059
回归一般的得到的是一个连续值，二分类需要的是0或者1（类别），那么怎么建立起连续值到类别的映射关系呢？逻辑回归是机器学习中常用的一种二分类算法，常用于疾病预测等“非黑即白”的分类，简单说就是在使用逻辑回归的任务中，标签数据的Y值要么是0要么是1。正是由于上面的特性，sigmoid函数可以被用来进行二分类，比如我们以0.5为界，将大于0.5的值归为类别1，小于0.5的归为类别0。这样子我们就完成了从输入数据的线性组合到概率的映射，然后根据一定的阈值将概率映射到类别，就完成了分类的过程。
《Pytorch深度学习实践》P7 处理多维特征的输入 笔记+代码：element-wise的理解、激活函数、代码和改进
大臣不想在月亮上上热搜
10-15 837
《Pytorch深度学习实践》P7 处理多维特征的输入 笔记+代码：element-wise的理解、激活函数、代码和改进
5.3 用PyTorch实现Logistic回归
Ting_28的博客
03-20 1888
Logistic回归常用于解决二分类问题。为了便于描述，我们分别从两个多元高斯分布 N₁（μ₁，Σ₁ ）、N₂（μ₂，Σ₂）中生成数据 x₁ 和 x₂，这两个多元高斯分布分别表示两个类别，分别设置其标签为 y₁ 和 y₂。PyTorch 的 torch.distributions 提供了 MultivariateNormal 构建多元高斯分布。下面代码设置两组不同的均值向量和协方差矩阵，μ₁（mul）和 μ₂（mul）是二维均值向量，Σ₁（sigmal）和Σ₂（sigma2）是2*2的协方差矩阵。
sigmoid & logistic
qq_36846729的博客
11-08 1363
1. 吴恩达老师视频中说sigmoid函数就是logistic函数。 2. 查阅复旦大学邱锡鹏老师关于深度学习的书，在第四章中写道： Sigmoid型函数是指一类S型曲线函数，为两端饱和函数。常用的Sigmoid型函数有Logistic函数和Tanh函数 ...
关于logistic、logit、log-odds、sigmoid、softmax、cross entropy
weixin_45783996的博客
03-27 8405
定义 sigmoid 函数：形状像S的函数。 logistic 函数：一种典型的sigmoid 函数，函数如下： logit函数：logistic 函数的反函数，也有logistic unit的意思，类似于probit相对于标准正态分布的分布函数（也是S型的呢）的反函数，即probability unit，就是通过概率找到随机变量的值： 也叫log-odds函数，因为p/(1-p)在统计学中叫做odds，几率、可能性、胜率的意思。 logistic模型（logit模型）：是一种回归模型，回归模型就是指对
【BCE】
m0_50089584的博客
12-04 1741
Certainly!
BCE损失+sigmoid搭配、CE损失+softmax激活函数
weixin_44505185的博客
04-26 2932
BCE损失+sigmoid搭配、CE损失+softmax激活函数
sigmoid 和 softmax，BCE与CE loss function
weixin_37721058的博客
09-15 9496
一句话概括 sigmoid 激活函数 二分类的激活函数 解决我是和不是的问题 对应二元交叉熵损失函数 softmax 激活函数 多分类的激活函数 解决我们中哪个是的问题 对应多元交叉熵损失函数 二分类推导 为什么用交叉商： 梯度下降的角度：从下面的推导过程可以看出来sigmoid对应的交叉商最后的梯度是一种残差。mse 是高斯分布的最大似然，二CE是多项式分布的最大似然。https://zhuan...
激活函数
sophicchen的专栏
12-09 1759
1. 激活函数 导数： 2.sigmoid函数 其实logistic函数也就是经常说的sigmoid函数，它的几何形状也就是一条sigmoid曲线（S型曲线）。A logistic function or logistic curve is a common “S” shape (sigmoid curve). 也就是说，sigmoid把一个值映射到0-1之间。 该函数具有如下...
激活函数总结
yx868yx的博客
06-06 2796
如果神经网络没有激活函数。在这种情况下，每个神经元只会利用权重和偏差对输入信息进行线性变换。虽然线性变换使神经网络更简单，但这个网络的功能会变得更弱，并无法从数据中学习复杂的模式。 没有激活函数的神经网络本质上只是一个线性回归模型。因此，我们对神经元的输入进行非线性变换，而神经网络中的这种非线性是由激活函数引入的。 sigmoid函数（sigmoid function）或logistic函数（logistic function）称为logistic函数的原因为该函数是两类别逻辑回归模型的预测表达式 1、Si
Logistic Regression的PyTorch实现
哈哈哈哈哈嗝哈哈哈
11-28 1892
Index 目录索引写在前面问题描述与分析Logistic Regression的数学原理logistic 函数PyTorch代码实现参考文章 写在前面 深度学习主要分为回归和分类这两个任务，本文将用一个分类的例子，使用PyTorch来搭建人工智能神经网络1，讲解如何搭建用通用模板来搭建一个完整的分类网络模型。【这是深度学习数学原理专题系列的第四篇文章】 问题描述与分析 本文的分类案例，是一个二分类问题，目的是要根据输入的学习时间，来预测能否考试合格，最终输出是考试通过的概率。 题目中给出的数据表明，学
softmax和sigmoid的区别
bblingbbling的博客
03-06 484
公式：sigmoid(x)=11+e−xsigmoid(x) = \frac{1}{1 + e^{-x}}sigmoid(x)=1+e−x1​函数曲线如下：导数公式：f(x)′=e−x(1+e−x)2=f(x)(1−f(x))f(x)\prime = \frac{ e^{-x}}{(1 + e^{-x})^2} = f(x)(1-f(x))f(x)′=(1+e−x)2e−x​=f(x)(1−f(x))导数曲线如下：sigmoid代码： softmax 公式： softmax(zi)=zi∑j=1nezjso
基于Logistic回归和Sigmoid函数的分类【机器学习】
shentanyue的博客
07-24 1万+
（一）认识Logistic回归（LR）分类器 首先，Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题，利用Logistic函数（或称为Sigmoid函数），自变量取值范围为(-INF, INF)，自变量的取值范围为(0,1)，函数形式为： 由于sigmoid函数的定义域是(-INF, +INF),而值域为(0, 1)。因此最基本的LR分类器适合于对两...
用pytorch实现logistic回归，要有数据准备、线性方程、激活函数、损失函数、优化算法、模型可视化，写出代码
03-23
以下是使用 PyTorch 实现 Logistic 回归的代码，包括数据准备、线性方程、激活函数、损失函数、优化算法和模型可视化： ```python import torch import torch.nn as nn import torch.optim as optim import matplotlib.pyplot as plt # 准备数据 x_train = torch.randn(100, 2) y_train = torch.zeros(100) y_train[(x_train[:, 0] + x_train[:, 1]) > 0] = 1 # 定义模型 class LogisticRegression(nn.Module): def __init__(self): super(LogisticRegression, self).__init__() self.linear = nn.Linear(2, 1) self.sigmoid = nn.Sigmoid() def forward(self, x): x = self.linear(x) x = self.sigmoid(x) return x model = LogisticRegression() # 定义损失函数和优化器 criterion = nn.BCELoss() optimizer = optim.SGD(model.parameters(), lr=0.1) # 训练模型 for epoch in range(1000): optimizer.zero_grad() y_pred = model(x_train) loss = criterion(y_pred.squeeze(), y_train) loss.backward() optimizer.step() # 可视化模型 w, b = model.linear.weight.squeeze().detach().numpy(), model.linear.bias.detach().numpy() plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train) x_min, x_max = plt.xlim() y_min, y_max = plt.ylim() xx, yy = torch.meshgrid(torch.linspace(x_min, x_max, 100), torch.linspace(y_min, y_max, 100)) z = model(torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)).detach().numpy().reshape(xx.shape) plt.contour(xx, yy, z, levels=[0.5]) plt.plot([-b/w[0], 0], [0, -b/w[1]]) plt.show() ``` 这段代码实现了一个简单的 Logistic 回归模型，使用 PyTorch 实现。其中，数据准备部分生成了一个二维的随机数据集，并根据数据的和是否大于 0 来生成标签；模型部分定义了一个包含线性层和 Sigmoid 激活函数的 Logistic 回归模型；损失函数使用了二元交叉熵损失函数；优化器使用了随机梯度下降算法。在训练模型后，使用 matplotlib 库可视化了模型的决策边界。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值