变量命名规则
ORB-SLAM2 中的变量遵循一套命名规则:
-
变量名的第一个字母为m,表示变量为某类的成员变量
-
变量名的第一、二个字母表示数据类型:
- p表示指针类型
- n表示int类型
- b表示bool类型
- s表示std::set 类型
- v表示std::vector类型
- l表示std::list 类型
- KF 表示KeyFrame类型
这种将变量类型写进变量名的命名方法叫做匈牙利命名法。
Converter.h
参数:
函数:
Frame.h
参数:
函数:
void Frame::ComputeStereoMatches( )
- 双目匹配函数
- 为左图的每一个特征点在右图中找到匹配点 \n
- 根据基线(有冗余范围)上描述子距离找到匹配, 再进行SAD精确定位 \n ‘
- 这里所说的SAD是一种双目立体视觉匹配算法,可参考[https://blog.csdn.net/u012507022/article/details/51446891]
- 最后对所有SAD的值进行排序, 剔除SAD值较大的匹配对,然后利用抛物线拟合得到亚像素精度的匹配 \n
- 这里所谓的亚像素精度,就是使用这个拟合得到一个小于一个单位像素的修正量,这样可以取得更好的估计结果,计算出来的点的深度也就越准确
- 匹配成功后会更新 mvuRight(ur) 和 mvDepth(Z)
/*两帧图像稀疏立体匹配(即:ORB特征点匹配,非逐像素的密集匹配,但依然满足行对齐)
* 输入:两帧立体矫正后的图像img_left 和 img_right 对应的orb特征点集
* 过程:
1. 行特征点统计. 统计img_right每一行上的ORB特征点集,便于使用立体匹配思路(行搜索/极线搜索)进行同名点搜索, 避免逐像素的判断.
2. 粗匹配. 根据步骤1的结果,对img_left第i行的orb特征点pi,在img_right的第i行上的orb特征点集中搜索相似orb特征点, 得到qi
3. 精确匹配. 以点qi为中心,半径为r的范围内,进行块匹配(归一化SAD),进一步优化匹配结果
4. 亚像素精度优化. 步骤3得到的视差为uchar/int类型精度,并不一定是真实视差,通过亚像素差值(抛物线插值)获取float精度的真实视差
5. 最优视差值/深度选择. 通过胜者为王算法(WTA)获取最佳匹配点。
6. 删除离群点(outliers). 块匹配相似度阈值判断,归一化sad最小,并不代表就一定是正确匹配,比如光照变化、弱纹理等会造成误匹配
* 输出:稀疏特征点视差图/深度图(亚像素精度)mvDepth 匹配结果 mvuRight
*/
步骤:
- 行特征点统计。将右图中的每个特征点放入其可能对应的行中。可能行号的范围为[ kpY + r , kpY - r ] , r 的大小需要根据图像金字塔的不同而改变。 (准备阶段)
- 以下开始粗匹配 + 精匹配的过程。对于立体矫正后的两张图,在列方向(x)存在最大视差maxd和最小视差mind,也即是左图中任何一点p,在右图上的匹配点的范围为应该是[p - maxd, p - mind], 而不需要遍历每一行所有的像素
- 已左图的一个特征点il为例,在右图搜索最相似的特征点ir
- 获取左图特征点il所在行,以及在右图对应行中可能的所有匹配点
- 计算理论上的最佳搜索距离并判断其是否合法。
- 粗配准。将左图特征点il与右图中的可能存在的匹配点,逐个比较,得到描述子距离最小的匹配点的描述子距离和索引。
- 判断,左图特征点il与待匹配点ic的空间尺度差不能超过2
- 获取右图待匹配点的x坐标,若超出理论搜索范围[ minU , maxU ],则可能是误匹配,舍弃
- 计算两点描述子之间的距离,找到距离最小的点对应的索引
- 图像块滑动窗口用SAD ( Sum of absolute differences ,差的绝对和) 实现精准匹配
- 判断,上一步计算的最小距离应满足预先设置的阈值
- 计算右图特征点x坐标和对应的金字塔尺度,然后计算尺度缩放后的猪油图特征点坐标
- 使用滑动窗口的方法,计算左图有右图特征点的SAD值,找到SAD值最小的点的索引,并保存每次的距离,用作后面的亚像素插值
- 亚像素插值, 使用最佳匹配点及其左右相邻点构成抛物线来得到最小sad的亚像素坐标
// 使用3点拟合抛物线的方式,用极小值代替之前计算的最优是差值 // \ / <- 由视差为14,15,16的相似度拟合的抛物线 // . .(16) // .14 .(15) <- int/uchar最佳视差值 // . // (14.5)<- 真实的视差值 // deltaR = 15.5 - 16 = -0.5 // 公式参考opencv sgbm源码中的亚像素插值公式 // 或论文<<On Building an Accurate Stereo Matching System on Graphics Hardware>> 公式7 - 找到最相似点,及其相邻的两个点,然后根据找二维次抛物线方程的最小值,计算deltaR
- 根据亚像素精度偏移量delta调整最佳匹配索引,并根据视差计算深度信息
- 删除离群点(outliers)。块匹配相似度阈值判断,归一化sad最小,并不代表就一定是匹配的,比如光照变化、弱纹理、无纹理等同样会造成误匹配,误匹配判断条件 norm_sad > 1.5 * 1.4 * median。 若误判,则将深度和右点索引都置位-1 。( 这一步是在找到所有左右对应点后进行的,通过先对所有点的深度进行排序,找到其中值,然后设定阈值 1.5 * 1.4 * median , 若深度大于阈值就是离散点,删除。)
vector<size_t> Frame::GetFeaturesInArea(const float &x, const float &y, const float &r, const int minLevel, const int maxLevel) const
- @brief 找到在 以x,y为中心,半径为r的圆形内且金字塔层级在[minLevel, maxLevel]的特征点
- @param[in] x 特征点坐标x
- @param[in] y 特征点坐标y
- @param[in] r 搜索半径
- @param[in] minLevel 最小金字塔层级
- @param[in] maxLevel 最大金字塔层级
- @return vector<size_t> 返回搜索到的候选匹配点id
步骤:
- 计算半径为r圆左右上下边界所在的网格列和行的id
- 遍历圆形区域内的所有网格,寻找满足条件的候选特征点,并将其index放到输出里
该函数是在已将N x N 的矩阵划分为多个小格子,每个小格子中可能包含特征点,通过对小格子进行查找特征点,这也是一种加速,减少了大量的循环时间。
bool Frame::isInFrustum(MapPoint *pMP, float viewingCosLimit)
- @brief 判断地图点是否在视野中
- 步骤
- Step 1 获得这个地图点的世界坐标,经过以下层层关卡的判断,通过的地图点才认为是在视野中
- Step 2 关卡一:将这个地图点变换到当前帧的相机坐标系下,如果深度值为正才能继续下一步。
- Step 3 关卡二:将地图点投影到当前帧的像素坐标,如果在图像有效范围内才能继续下一步。
- Step 4 关卡三:计算地图点到相机中心的距离,如果在有效距离范围内才能继续下一步。
- Step 5 关卡四:计算当前相机指向地图点向量和地图点的平均观测方向夹角,小于60°才能进入下一步。
- Step 6 根据地图点到光心的距离来预测一个尺度(仿照特征点金字塔层级)
- Step 7 记录计算得到的一些参数
- @param[in] pMP 当前地图点
- @param[in] viewingCosLimit 当前相机指向地图点向量和地图点的平均观测方向夹角余弦阈值
- @return true 地图点合格,且在视野内
- @return false 地图点不合格,抛弃
FrameDrawer.h
参数:
函数:
Initializer.h
参数:
函数:
void Initializer::Normalize(const vectorcv::KeyPoint &vKeys, vectorcv::Point2f &vNormalizedPoints, cv::Mat &T)
- @brief 归一化特征点到同一尺度,作为后续normalize DLT的输入
- [x’ y’ 1]’ = T * [x y 1]’
- 归一化后x’, y’的均值为0,sum(abs(x_i’-0))=1,sum(abs((y_i’-0))=1
- 为什么要归一化?
- 在相似变换之后(点在不同的坐标系下),他们的单应性矩阵是不相同的
- 如果图像存在噪声,使得点的坐标发生了变化,那么它的单应性矩阵也会发生变化
- 我们采取的方法是将点的坐标放到同一坐标系下,并将缩放尺度也进行统一
- 对同一幅图像的坐标进行相同的变换,不同图像进行不同变换
- 缩放尺度是为了让噪声对于图像的影响在一个数量级上
- Step 1 计算特征点X,Y坐标的均值
- Step 2 计算特征点X,Y坐标离均值的平均偏离程度
- Step 3 将x坐标和y坐标分别进行尺度归一化,使得x坐标和y坐标的一阶绝对矩分别为1
- Step 4 计算归一化矩阵:其实就是前面做的操作用矩阵变换来表示而已
- @param[in] vKeys 待归一化的特征点
- @param[in & out] vNormalizedPoints 特征点归一化后的坐标
- @param[in & out] T 归一化特征点的变换矩阵
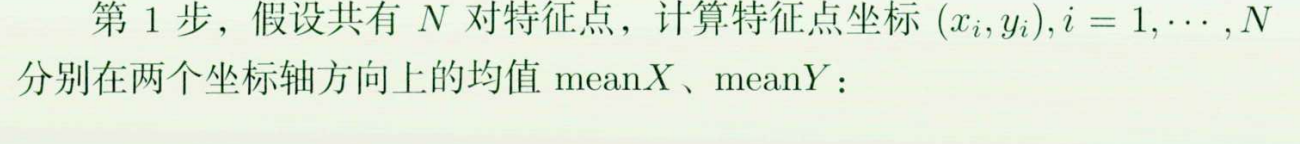


cv::Mat Initializer::ComputeH21( const vectorcv::Point2f &vP1, const vectorcv::Point2f &vP2)
- @brief 用DLT方法求解单应矩阵H
- 这里最少用4对点就能够求出来,不过这里为了统一还是使用了8对点求最小二乘解
- @param[in] vP1 参考帧中归一化后的特征点
- @param[in] vP2 当前帧中归一化后的特征点
- @return cv::Mat 计算的单应矩阵H
- 最后返回的是3x3的矩阵
// 基本原理:见附件推导过程:
// |x'| | h1 h2 h3 ||x|
// |y'| = a | h4 h5 h6 ||y| 简写: x' = a H x, a为一个尺度因子
// |1 | | h7 h8 h9 ||1|
// 使用DLT(direct linear tranform)求解该模型
// x' = a H x
// ---> (x') 叉乘 (H x) = 0 (因为方向相同) (取前两行就可以推导出下面的了)
// ---> Ah = 0
// A = | 0 0 0 -x -y -1 xy' yy' y'| h = | h1 h2 h3 h4 h5 h6 h7 h8 h9 |
// |-x -y -1 0 0 0 xx' yx' x'|
// 通过SVD求解Ah = 0,A^T*A最小特征值对应的特征向量即为解
// 其实也就是右奇异值矩阵v的最后一列,即vT的最后一行
该函数中,奇异值分解是在设置好数据后,调用opencv中的函数
//使用opencv提供的进行奇异值分解的函数
cv::SVDecomp(A, //输入,待进行奇异值分解的矩阵
w, //输出,奇异值矩阵
u, //输出,矩阵U
vt, //输出,矩阵V^T
cv::SVD::MODIFY_A | //输入,MODIFY_A是指允许计算函数可以修改待分解的矩阵,官方文档上说这样可以加快计算速度、节省内存
cv::SVD::FULL_UV); //FULL_UV=把U和VT补充成单位正交方阵
float Initializer::CheckHomography(
const cv::Mat &H21, //从参考帧到当前帧的单应矩阵
const cv::Mat &H12, //从当前帧到参考帧的单应矩阵
vector &vbMatchesInliers, //匹配好的特征点对的Inliers标记
float sigma) //估计误差
- @brief 对给定的单应矩阵计算双向重投影并进行打分,
- 需要使用到卡方检验的知识
- @param[in] H21 从参考帧到当前帧的单应矩阵
- @param[in] H12 从当前帧到参考帧的单应矩阵
- @param[in] vbMatchesInliers 匹配好的特征点对的Inliers标记
- @param[in] sigma 方差,默认为1
- @return float 返回单应矩阵得分
// 说明:在已值n维观测数据误差服从N(0,sigma)的高斯分布时
// 其误差加权最小二乘结果为 sum_error = SUM(e(i)^T * Q^(-1) * e(i))
// 其中:e(i) = [e_x,e_y,...]^T, Q维观测数据协方差矩阵,即sigma * sigma组成的协方差矩阵
// 误差加权最小二次结果越小,说明观测数据精度越高
// 那么,score = SUM((th - e(i)^T * Q^(-1) * e(i)))的分数就越高
// 算法目标: 检查单应变换矩阵
// 检查方式:通过H矩阵,进行参考帧和当前帧之间的双向投影,并计算起加权最小二乘投影误差
// 算法流程
// input: 单应性矩阵 H21, H12, 匹配点集 mvKeys1
// do:
// for p1(i), p2(i) in mvKeys:
// error_i1 = ||p2(i) - H21 * p1(i)||2
// error_i2 = ||p1(i) - H12 * p2(i)||2
//
// w1 = 1 / sigma / sigma
// w2 = 1 / sigma / sigma
//
// if error1 < th
// score += th - error_i1 * w1
// if error2 < th
// score += th - error_i2 * w2
//
// if error_1i > th or error_2i > th
// p1(i), p2(i) are inner points
// vbMatchesInliers(i) = true
// else
// p1(i), p2(i) are outliers
// vbMatchesInliers(i) = false
// end
// end
// output: score, inliers
最终选择所有迭代中得分最高的一组对应的单应矩阵最为最优解。
cv::Mat Initializer::ComputeF21( const vectorcv::Point2f &vP1,
const vector<cv::Point2f> &vP2)
- @brief 根据特征点匹配求fundamental matrix(normalized 8点法)
- 注意F矩阵有秩为2的约束,所以需要两次SVD分解
- @param[in] vP1 参考帧中归一化后的特征点
- @param[in] vP2 当前帧中归一化后的特征点
- @return cv::Mat 最后计算得到的基础矩阵F
// 原理详见附件推导
// x’Fx = 0 整理可得:Af = 0
// A = | x’x x’y x’ y’x y’y y’ x y 1 |, f = | f1 f2 f3 f4 f5 f6 f7 f8 f9 |
// 通过SVD求解Af = 0,A’A最小特征值对应的特征向量即为解
步骤:
- 构造A矩阵
- 使用cv::SVDecomp()函数,进行奇异值分解
- v的最后一列(vT的最后一行)即为Fpre,并将Fpre变为3x3矩阵
- 基础矩阵的秩为2,而我们不敢保证计算得到的这个结果的秩为2,所以需要通过第二次奇异值分解,来强制使其秩为2。对初步得来的基础矩阵进行第2次奇异值分解
- 秩2约束,强制将第3个奇异值设置为0
- 重新组合好满足秩约束的基础矩阵,作为最终计算结果返回
float Initializer::CheckFundamental(const cv::Mat &F21,
vector< bool> &vbMatchesInliers, float sigma)
- @brief 对给定的Fundamental matrix打分
- @param[in] F21 当前帧和参考帧之间的基础矩阵
- @param[in] vbMatchesInliers 匹配的特征点对属于inliers的标记
- @param[in] sigma 方差,默认为1
- @return float 返回得分
// 说明:在已值n维观测数据误差服从N(0,sigma)的高斯分布时
// 其误差加权最小二乘结果为 sum_error = SUM(e(i)^T * Q^(-1) * e(i))
// 其中:e(i) = [e_x,e_y,...]^T, Q维观测数据协方差矩阵,即sigma * sigma组成的协方差矩阵
// 误差加权最小二次结果越小,说明观测数据精度越高
// 那么,score = SUM((th - e(i)^T * Q^(-1) * e(i)))的分数就越高
// 算法目标:检查基础矩阵
// 检查方式:利用对极几何原理 p2^T * F * p1 = 0
// 假设:三维空间中的点 P 在 img1 和 img2 两图像上的投影分别为 p1 和 p2(两个为同名点)
// 则:p2 一定存在于极线 l2 上,即 p2*l2 = 0. 而l2 = F*p1 = (a, b, c)^T
// 所以,这里的误差项 e 为 p2 到 极线 l2 的距离,如果在直线上,则 e = 0
// 根据点到直线的距离公式:d = (ax + by + c) / sqrt(a * a + b * b)
// 所以,e = (a * p2.x + b * p2.y + c) / sqrt(a * a + b * b)
// 算法流程
// input: 基础矩阵 F 左右视图匹配点集 mvKeys1
// do:
// for p1(i), p2(i) in mvKeys:
// l2 = F * p1(i)
// l1 = p2(i) * F
// error_i1 = dist_point_to_line(x2,l2)
// error_i2 = dist_point_to_line(x1,l1)
//
// w1 = 1 / sigma / sigma
// w2 = 1 / sigma / sigma
//
// if error1 < th
// score += thScore - error_i1 * w1
// if error2 < th
// score += thScore - error_i2 * w2
//
// if error_1i > th or error_2i > th
// p1(i), p2(i) are inner points
// vbMatchesInliers(i) = true
// else
// p1(i), p2(i) are outliers
// vbMatchesInliers(i) = false
// end
// end
// output: score, inliers
步骤:
- 提取基础矩阵中的元素数据,并初始化阈值参数
- 计算img1和img2在估计F时的score值,主要是判断极线的距离,以一对点为例
- 提取参考帧与当前帧之间的匹配点对,并得到点的坐标
- 计算img1上的点在img2上投影得到的极线l2 = F21 * p1 = (a2,b2,c2)
- 计算误差 e = (a * p2.x + b * p2.y + c) / sqrt(a * a + b * b),最后除以sigma的平方
- 误差大于阈值就说明这个点是Outlier ,舍弃,不计算得分;否则,计算得分
- 计算img2上的点在 img1 上投影得到的极线 l1= p2 * F21 = (a1,b1,c1)
- 计算误差 e = (a * p2.x + b * p2.y + c) / sqrt(a * a + b * b),最后除以sigma的平方
- 误差大于阈值就说明这个点是Outlier,舍弃,不计算得分;否则,计算得分
- 返回评分
bool Initializer::ReconstructF(vector< bool> &vbMatchesInliers, cv::Mat &F21, cv::Mat &K, cv::Mat &R21, cv::Mat &t21, vector< cv::Point3f> &vP3D, vector< bool> &vbTriangulated, float minParallax, int minTriangulated)
- @brief 从基础矩阵F中求解位姿R,t及三维点
- F分解出E,E有四组解,选择计算的有效三维点(在摄像头前方、投影误差小于阈值、视差角大于阈值)最多的作为最优的解
- @param[in] vbMatchesInliers 匹配好的特征点对的Inliers标记
- @param[in] F21 从参考帧到当前帧的基础矩阵
- @param[in] K 相机的内参数矩阵
- @param[in & out] R21 计算好的相机从参考帧到当前帧的旋转
- @param[in & out] t21 计算好的相机从参考帧到当前帧的平移
- @param[in & out] vP3D 三角化测量之后的特征点的空间坐标
- @param[in & out] vbTriangulated 特征点三角化成功的标志
- @param[in] minParallax 认为三角化有效的最小视差角
- @param[in] minTriangulated 最小三角化点数量
- @return true 成功初始化
- @return false 初始化失败
步骤:
- 统计有效匹配点的个数,并用N表示(在后面用来判断R、t是否有效)
- 根据基础矩阵和相机的内参数矩阵计算本质矩阵。 E = K.T * F * K
- 从本质矩阵求解两个R解和两个t解,共四组解 。使用DecomposeE( )函数求解
- 分别验证求解的4种R和t的组合,选出最佳组合。
- 原理:若某一组合使恢复得到的3D点位于相机正前方的数量最多,那么该组合就是最佳组
- 实现:根据计算的解组合成为四种情况,并依次调用 Initializer::CheckRT() 进行检查,得到可以进行三角化测量的点的数目
- 1、使用同样的匹配点分别检查四组解,记录当前计算的3D点在摄像头前方且投影误差小于阈值的个数,记为有效3D点个数
- 2、选取最大可三角化测量的点的数目
- 3、确定最小的可以三角化的点数 。
- 在0.9倍的内点数 和 指定值minTriangulated =50 中取最大的,也就是说至少50个
- 统计四组解中重建的有效3D点个数 > 0.7 * maxGood 的解的数目
- 4、 四个结果中如果没有明显的最优结果,或者没有足够数量的三角化点,则返回失败
- 条件1: 如果四组解能够重建的最多3D点个数小于所要求的最少3D点个数(mMinGood),失败
- 条件2: 如果存在两组及以上的解能三角化出 >0.7*maxGood的点,说明没有明显最优结果,失败
- 5、选择最佳解记录结果
- 条件1: 有效重建最多的3D点,即maxGood == nGoodx,也即是位于相机前方的3D点个数最多
- 条件2: 三角化视差角 parallax 必须大于最小视差角 minParallax,角度越大3D点越稳定
- 若都满足,则存储3D坐标、获取特征点向量的三角化测量标记、存储相机姿态
bool Initializer::ReconstructH(vector< bool> &vbMatchesInliers, cv::Mat &H21, cv::Mat &K, cv::Mat &R21, cv::Mat &t21, vector< cv::Point3f> &vP3D, vector< bool> &vbTriangulated, float minParallax, int minTriangulated)
- @brief 用H矩阵恢复R, t和三维点
- H矩阵分解常见有两种方法:Faugeras SVD-based decomposition 和 Zhang SVD-based decomposition
- 代码使用了Faugeras SVD-based decomposition算法,参考文献
- Motion and structure from motion in a piecewise planar environment. International Journal of Pattern Recognition and Artificial Intelligence, 1988
- @param[in] vbMatchesInliers 匹配点对的内点标记
- @param[in] H21 从参考帧到当前帧的单应矩阵
- @param[in] K 相机的内参数矩阵
- @param[in & out] R21 计算出来的相机旋转
- @param[in & out] t21 计算出来的相机平移
- @param[in & out] vP3D 世界坐标系下,三角化测量特征点对之后得到的特征点的空间坐标
- @param[in & out] vbTriangulated 特征点是否成功三角化的标记
- @param[in] minParallax 对特征点的三角化测量中,认为其测量有效时需要满足的最小视差角(如果视差角过小则会引起非常大的观测误差),单位是角度
- @param[in] minTriangulated 为了进行运动恢复,所需要的最少的三角化测量成功的点个数
- @return true 单应矩阵成功计算出位姿和三维点
- @return false 初始化失败
// 目的 :通过单应矩阵H恢复两帧图像之间的旋转矩阵R和平移向量T
// 参考 :Motion and structure from motion in a piecewise plannar environment.
// International Journal of Pattern Recognition and Artificial Intelligence, 1988
// https://www.researchgate.net/publication/243764888_Motion_and_Structure_from_Motion_in_a_Piecewise_Planar_Environment
// 流程:
// 1. 根据H矩阵的奇异值d'= d2 或者 d' = -d2 分别计算 H 矩阵分解的 8 组解
// 1.1 讨论 d' > 0 时的 4 组解
// 1.2 讨论 d' < 0 时的 4 组解
// 2. 对 8 组解进行验证,并选择产生相机前方最多3D点的解为最优解
// 统计匹配的特征点对中属于内点(Inlier)或有效点个数
int N=0;
for(size_t i=0, iend = vbMatchesInliers.size() ; i<iend; i++)
if(vbMatchesInliers[i])
N++;
// We recover 8 motion hypotheses using the method of Faugeras et al.
// Motion and structure from motion in a piecewise planar environment.
// International Journal of Pattern Recognition and Artificial Intelligence, 1988
// 参考SLAM十四讲第二版p170-p171
// H = K * (R - t * n / d) * K_inv
// 其中: K表示内参数矩阵
// K_inv 表示内参数矩阵的逆
// R 和 t 表示旋转和平移向量
// n 表示平面法向量
// 令 H = K * A * K_inv
// 则 A = k_inv * H * k
cv::Mat invK = K.inv();
cv::Mat A = invK*H21*K;
// 对矩阵A进行SVD分解
// A 等待被进行奇异值分解的矩阵
// w 奇异值矩阵
// U 奇异值分解左矩阵
// Vt 奇异值分解右矩阵,注意函数返回的是转置
// cv::SVD::FULL_UV 全部分解
// A = U * w * Vt
cv::Mat U,w,Vt,V;
cv::SVD::compute(A, w, U, Vt, cv::SVD::FULL_UV);
// 根据文献eq(8),计算关联变量
V=Vt.t();
// 计算变量s = det(U) * det(V)
// 因为det(V)==det(Vt), 所以 s = det(U) * det(Vt)
float s = cv::determinant(U)*cv::determinant(Vt);
// 取得矩阵的各个奇异值
float d1 = w.at<float>(0);
float d2 = w.at<float>(1);
float d3 = w.at<float>(2);
// SVD分解正常情况下特征值di应该是正的,且满足d1>=d2>=d3
if(d1/d2<1.00001 || d2/d3<1.00001) {
return false;
}
// 在ORBSLAM中没有对奇异值 d1 d2 d3按照论文中描述的关系进行分类讨论, 而是直接进行了计算
// 定义8中情况下的旋转矩阵、平移向量和空间向量
vector<cv::Mat> vR, vt, vn;
vR.reserve(8);
vt.reserve(8);
vn.reserve(8);
// Step 1.1 讨论 d' > 0 时的 4 组解
// 根据论文eq.(12)有
// x1 = e1 * sqrt((d1 * d1 - d2 * d2) / (d1 * d1 - d3 * d3))
// x2 = 0
// x3 = e3 * sqrt((d2 * d2 - d2 * d2) / (d1 * d1 - d3 * d3))
// 令 aux1 = sqrt((d1*d1-d2*d2)/(d1*d1-d3*d3))
// aux3 = sqrt((d2*d2-d3*d3)/(d1*d1-d3*d3))
// 则
// x1 = e1 * aux1
// x3 = e3 * aux2
// 因为 e1,e2,e3 = 1 or -1
// 所以有x1和x3有四种组合
// x1 = {aux1,aux1,-aux1,-aux1}
// x3 = {aux3,-aux3,aux3,-aux3}
float aux1 = sqrt((d1*d1-d2*d2)/(d1*d1-d3*d3));
float aux3 = sqrt((d2*d2-d3*d3)/(d1*d1-d3*d3));
float x1[] = {aux1,aux1,-aux1,-aux1};
float x3[] = {aux3,-aux3,aux3,-aux3};
// 根据论文eq.(13)有
// sin(theta) = e1 * e3 * sqrt(( d1 * d1 - d2 * d2) * (d2 * d2 - d3 * d3)) /(d1 + d3)/d2
// cos(theta) = (d2* d2 + d1 * d3) / (d1 + d3) / d2
// 令 aux_stheta = sqrt((d1*d1-d2*d2)*(d2*d2-d3*d3))/((d1+d3)*d2)
// 则 sin(theta) = e1 * e3 * aux_stheta
// cos(theta) = (d2*d2+d1*d3)/((d1+d3)*d2)
// 因为 e1 e2 e3 = 1 or -1
// 所以 sin(theta) = {aux_stheta, -aux_stheta, -aux_stheta, aux_stheta}
float aux_stheta = sqrt((d1*d1-d2*d2)*(d2*d2-d3*d3))/((d1+d3)*d2);
float ctheta = (d2*d2+d1*d3)/((d1+d3)*d2);
float stheta[] = {aux_stheta, -aux_stheta, -aux_stheta, aux_stheta};
// 计算旋转矩阵 R'
//根据不同的e1 e3组合所得出来的四种R t的解
// | ctheta 0 -aux_stheta| | aux1|
// Rp = | 0 1 0 | tp = | 0 |
// | aux_stheta 0 ctheta | |-aux3|
// | ctheta 0 aux_stheta| | aux1|
// Rp = | 0 1 0 | tp = | 0 |
// |-aux_stheta 0 ctheta | | aux3|
// | ctheta 0 aux_stheta| |-aux1|
// Rp = | 0 1 0 | tp = | 0 |
// |-aux_stheta 0 ctheta | |-aux3|
// | ctheta 0 -aux_stheta| |-aux1|
// Rp = | 0 1 0 | tp = | 0 |
// | aux_stheta 0 ctheta | | aux3|
// 开始遍历这四种情况中的每一种
for(int i=0; i<4; i++)
{
//生成Rp,就是eq.(8) 的 R'
cv::Mat Rp=cv::Mat::eye(3,3,CV_32F);
Rp.at<float>(0,0)=ctheta;
Rp.at<float>(0,2)=-stheta[i];
Rp.at<float>(2,0)=stheta[i];
Rp.at<float>(2,2)=ctheta;
// eq.(8) 计算R
cv::Mat R = s*U*Rp*Vt;
// 保存
vR.push_back(R);
// eq. (14) 生成tp
cv::Mat tp(3,1,CV_32F);
tp.at<float>(0)=x1[i];
tp.at<float>(1)=0;
tp.at<float>(2)=-x3[i];
tp*=d1-d3;
// 这里虽然对t有归一化,并没有决定单目整个SLAM过程的尺度
// 因为CreateInitialMapMonocular函数对3D点深度会缩放,然后反过来对 t 有改变
// eq.(8)恢复原始的t
cv::Mat t = U*tp;
vt.push_back(t/cv::norm(t));
// 构造法向量np
cv::Mat np(3,1,CV_32F);
np.at<float>(0)=x1[i];
np.at<float>(1)=0;
np.at<float>(2)=x3[i];
// eq.(8) 恢复原始的法向量
cv::Mat n = V*np;
//看PPT 16页的图,保持平面法向量向上
if(n.at<float>(2)<0)
n=-n;
// 添加到vector
vn.push_back(n);
}
// Step 1.2 讨论 d' < 0 时的 4 组解
float aux_sphi = sqrt((d1*d1-d2*d2)*(d2*d2-d3*d3))/((d1-d3)*d2);
// cos_theta项
float cphi = (d1*d3-d2*d2)/((d1-d3)*d2);
// 考虑到e1,e2的取值,这里的sin_theta有两种可能的解
float sphi[] = {aux_sphi, -aux_sphi, -aux_sphi, aux_sphi};
// 对于每种由e1 e3取值的组合而形成的四种解的情况
for(int i=0; i<4; i++)
{
// 计算旋转矩阵 R'
cv::Mat Rp=cv::Mat::eye(3,3,CV_32F);
Rp.at<float>(0,0)=cphi;
Rp.at<float>(0,2)=sphi[i];
Rp.at<float>(1,1)=-1;
Rp.at<float>(2,0)=sphi[i];
Rp.at<float>(2,2)=-cphi;
// 恢复出原来的R
cv::Mat R = s*U*Rp*Vt;
// 然后添加到vector中
vR.push_back(R);
// 构造tp
cv::Mat tp(3,1,CV_32F);
tp.at<float>(0)=x1[i];
tp.at<float>(1)=0;
tp.at<float>(2)=x3[i];
tp*=d1+d3;
// 恢复出原来的t
cv::Mat t = U*tp;
// 归一化之后加入到vector中,要提供给上面的平移矩阵都是要进行过归一化的
vt.push_back(t/cv::norm(t));
// 构造法向量np
cv::Mat np(3,1,CV_32F);
np.at<float>(0)=x1[i];
np.at<float>(1)=0;
np.at<float>(2)=x3[i];
// 恢复出原来的法向量
cv::Mat n = V*np;
// 保证法向量指向上方
if(n.at<float>(2)<0)
n=-n;
// 添加到vector中
vn.push_back(n);
}
// 最好的good点
int bestGood = 0;
// 其次最好的good点
int secondBestGood = 0;
// 最好的解的索引,初始值为-1
int bestSolutionIdx = -1;
// 最大的视差角
float bestParallax = -1;
// 存储最好解对应的,对特征点对进行三角化测量的结果
vector<cv::Point3f> bestP3D;
// 最佳解所对应的,那些可以被三角化测量的点的标记
vector<bool> bestTriangulated;
// Instead of applying the visibility constraints proposed in the WFaugeras' paper (which could fail for points seen with low parallax)
// We reconstruct all hypotheses and check in terms of triangulated points and parallax
// Step 2. 对 8 组解进行验证,并选择产生相机前方最多3D点的解为最优解
for(size_t i=0; i<8; i++)
{
// 第i组解对应的比较大的视差角
float parallaxi;
// 三角化测量之后的特征点的空间坐标
vector<cv::Point3f> vP3Di;
// 特征点对是否被三角化的标记
vector<bool> vbTriangulatedi;
// 调用 Initializer::CheckRT(), 计算good点的数目
int nGood = CheckRT(vR[i],vt[i], //当前组解的旋转矩阵和平移向量
mvKeys1,mvKeys2, //特征点
mvMatches12,vbMatchesInliers, //特征匹配关系以及Inlier标记
K, //相机的内参数矩阵
vP3Di, //存储三角化测量之后的特征点空间坐标的
4.0*mSigma2, //三角化过程中允许的最大重投影误差
vbTriangulatedi, //特征点是否被成功进行三角测量的标记
parallaxi); // 这组解在三角化测量的时候的比较大的视差角
// 更新历史最优和次优的解
// 保留最优的和次优的解.保存次优解的目的是看看最优解是否突出
if(nGood>bestGood)
{
// 如果当前组解的good点数是历史最优,那么之前的历史最优就变成了历史次优
secondBestGood = bestGood;
// 更新历史最优点
bestGood = nGood;
// 最优解的组索引为i(就是当前次遍历)
bestSolutionIdx = i;
// 更新变量
bestParallax = parallaxi;
bestP3D = vP3Di;
bestTriangulated = vbTriangulatedi;
}
// 如果当前组的good计数小于历史最优但却大于历史次优
else if(nGood>secondBestGood)
{
// 说明当前组解是历史次优点,更新之
secondBestGood = nGood;
}
}
// Step 3 选择最优解。要满足下面的四个条件
// 1. good点数最优解明显大于次优解,这里取0.75经验值
// 2. 视角差大于规定的阈值
// 3. good点数要大于规定的最小的被三角化的点数量
// 4. good数要足够多,达到总数的90%以上
if(secondBestGood<0.75*bestGood &&
bestParallax>=minParallax &&
bestGood>minTriangulated &&
bestGood>0.9*N)
{
// 从最佳的解的索引访问到R,t
vR[bestSolutionIdx].copyTo(R21);
vt[bestSolutionIdx].copyTo(t21);
// 获得最佳解时,成功三角化的三维点,以后作为初始地图点使用
vP3D = bestP3D;
// 获取特征点的被成功进行三角化的标记
vbTriangulated = bestTriangulated;
//返回真,找到了最好的解
return true;
}
return false;
void Initializer::DecomposeE(const cv::Mat &E, cv::Mat &R1, cv::Mat &R2, cv::Mat &t)
- @brief 分解Essential矩阵得到R,t
- 分解E矩阵将得到4组解,这4组解分别为[R1,t],[R1,-t],[R2,t],[R2,-t]
- 参考:Multiple View Geometry in Computer Vision - Result 9.19 p259
- @param[in] E 本质矩阵
- @param[in & out] R1 旋转矩阵1
- @param[in & out] R2 旋转矩阵2
- @param[in & out] t 平移向量,另外一个取相反数
步骤:
- 对本质矩阵进行奇异值分解,cv::SVD::compute(E,w,u,vt);
- 左奇异值矩阵U的最后一列就是t,并对其进行归一化
- 构建绕Z轴旋转的旋转矩阵W
- 计算R1,R2 。 R1=u* W * vt
- 若R1或R2的行列式为负值,则对R1或R2取反
void Initializer::Triangulate( const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
- @brief 给定投影矩阵P1,P2和图像上的匹配特征点kp1,kp2,从而计算三维点坐标
- @param[in] kp1 特征点, in reference frame
- @param[in] kp2 特征点, in current frame
- @param[in] P1 投影矩阵P1
- @param[in] P2 投影矩阵P2
- @param[in & out] x3D 计算的三维点



// 原理
// Trianularization: 已知匹配特征点对{x x'} 和 各自相机矩阵{P P'}, 估计三维点 X
// x' = P'X x = PX
// 它们都属于 x = aPX模型
// |X|
// |x| |p1 p2 p3 p4 ||Y| |x| |--p0--||.|
// |y| = a |p5 p6 p7 p8 ||Z| ===>|y| = a|--p1--||X|
// |z| |p9 p10 p11 p12||1| |z| |--p2--||.|
// 采用DLT的方法:x叉乘PX = 0
// |yp2 - p1| |0|
// |p0 - xp2| X = |0|
// |xp1 - yp0| |0|
// 两个点:
// |yp2 - p1 | |0|
// |p0 - xp2 | X = |0| ===> AX = 0
// |y'p2' - p1' | |0|
// |p0' - x'p2'| |0|
// 变成程序中的形式:
// |xp2 - p0 | |0|
// |yp2 - p1 | X = |0| ===> AX = 0
// |x'p2'- p0'| |0|
// |y'p2'- p1'| |0|
// 然后就组成了一个四元一次正定方程组,SVD求解,右奇异矩阵的最后一行就是最终的解.
//这个就是上面注释中的矩阵A
cv::Mat A(4,4,CV_32F);
//构造参数矩阵A
A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);
//奇异值分解的结果
cv::Mat u,w,vt;
//对系数矩阵A进行奇异值分解
cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
//根据前面的结论,奇异值分解右矩阵的最后一行其实就是解,原理类似于前面的求最小二乘解,四个未知数四个方程正好正定
//别忘了我们更习惯用列向量来表示一个点的空间坐标
x3D = vt.row(3).t();
//为了符合其次坐标的形式,使最后一维为1
x3D = x3D.rowRange(0,3)/x3D.at<float>(3);
int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector< cv::KeyPoint> &vKeys1, const vector< cv::KeyPoint> &vKeys2, const vector< Match> &vMatches12, vector< bool> &vbMatchesInliers,
const cv::Mat &K, vector< cv::Point3f> &vP3D, float th2, vector< bool> &vbGood, float ¶llax)
- @brief 用位姿来对特征匹配点三角化,从中筛选中合格的三维点
- @param[in] R 旋转矩阵R
- @param[in] t 平移矩阵t
- @param[in] vKeys1 参考帧特征点
- @param[in] vKeys2 当前帧特征点
- @param[in] vMatches12 两帧特征点的匹配关系
- @param[in] vbMatchesInliers 特征点对内点标记
- @param[in] K 相机内参矩阵
- @param[in & out] vP3D 三角化测量之后的特征点的空间坐标
- @param[in] th2 重投影误差的阈值
- @param[in & out] vbGood 标记成功三角化点?
- @param[in & out] parallax 计算出来的比较大的视差角(注意不是最大,具体看后面代码)
- @return int
步骤:
-
计算相机的投影矩阵。投影矩阵P是一个3x4的矩阵,可以将空间中的一个点投影到平面上,获得其平面坐标,这里均指的是齐次坐标。
-
对于第一个相机是 P1=K*[I|0]。以第一个相机的光心作为世界坐标系, 定义相机的投影矩阵。第一个相机的光心设置为世界坐标系下的原点
-
计算第二个相机的投影矩阵 P2=K*[R|t]。计算第二个相机的光心在世界坐标系下的坐标。
-
开始遍历所有的特征点对
- 跳过outliers
- 获取特征点对,调用Triangulate()函数进行三角化,得到三角化测量之后的3D点坐标。(下面几步为检查三维点是否合法)
- 第一关:检查三角化的三维点坐标是否合法(非无穷值)。只要三角测量的结果中有一个是无穷大的就说明三角化失败,跳过对当前点的处理,进行下一对特征点的遍历
- 第二关:通过三维点深度值正负、两相机光心视差角大小来检查是否合法 (这个地方,原代码中的cosParallax应该是余弦值,但是结合后面的部分看,作者将其作为弧度值,就是arccos,这里很奇怪,但是我加了arccos后,最后结果没什么区别。这个地方阈值比较为小于,我的想法是两张图片光心之间的加入如果太小,说明两张图片很近,那么他们进行匹配、计算关键帧平移旋转等后续操作时,可能会导致很差的效果或者根本就检测不到变化,通过修改后实验事实证明也确实是这样,无法初始化关键帧和地图点)
- 第三关:计算空间点在参考帧和当前帧上的重投影误差,如果大于阈值则舍弃
- 统计经过检验的3D点个数,记录3D点视差角 。如果运行到这里就说明当前遍历的这个特征点对靠谱,经过了重重检验,说明是一个合格的点,称之为good点。
-
得到3D点中较小的视差角,并且转换成为角度制表示。按弧度值大小排序,排序后并没有取最小的视差角,而是取一个较小的视差角,作者的做法:如果经过检验过后的有效3D点小于50个,那么就取最后那个最小的视差角(cos值最大),如果大于50个,就取排名第50个的较小的视差角即可,为了避免3D点太多时出现太小的视差角。
KeyFrame.h
参数:
函数:
UpdateConnections()
更新关键帧之间的连接图。

步骤:
- 首先获得该关键帧的所有MapPoint点,统计观测到这些3d点的每个关键帧与其它所有关键帧之间的共视程度,对每一个找到的关键帧,建立一条边,边的权重是该关键帧与当前关键帧公共3d点的个数。
- 找到对应权重最大的关键帧。并且该权重必须大于一个阈值,如果没有超过该阈值的权重,那么就只保留权重最大的边(与其它关键帧的共视程度比较高)
- 对这些连接按照权重从大到小进行排序,以方便将来的处理。更新完covisibility图之后,如果没有初始化过,则初始化为连接权重最大的边(与其它关键帧共视程度最高的那个关键帧),类似于最大生成树
AddConnection(KeyFrame *pKF, const int &weight)
- @brief 为当前关键帧新建或更新和其他关键帧的连接权重
- @param[in] pKF 和当前关键帧共视的其他关键帧
- @param[in] weight 当前关键帧和其他关键帧的权重(共视地图点数目)
步骤:
- if (该关键帧没有建立连接),则建立新的连接
- else if (权重与之前不同 ),则更新权重
- else return ;
- 最后更新最佳共视。( 连接关系变化就要更新最佳共视,主要是重新进行排序)
UpdateBestCovisibles()
- @brief 按照权重从大到小对连接(共视)的关键帧进行排序
- 更新后的变量存储在mvpOrderedConnectedKeyFrames和mvOrderedWeights中
步骤:
因为map<key,value> 是根据key排序的,需要转换为pair< 权重,关键帧 >型,然后使用sort排序
- 将map型转换为pair型
- 使用sort根据权重从小到大排序
- 分别使用list.push_front() 将关键帧和权重分别按权重从大到小存储
- 将两个list类的值赋值给成员变量mvpOrderedConnectedKeyFrames、mvOrderedWeights(权重从大到小排列,都是vector容器)
vector<KeyFrame*> KeyFrame::GetBestCovisibilityKeyFrames(const int &N)
- @brief 得到与该关键帧连接的前N个最强共视关键帧(已按权值排序)
- @param[in] N 设定要取出的关键帧数目
- @return vector<KeyFrame*> 满足权重条件的关键帧集合
vector<KeyFrame*> KeyFrame::GetCovisiblesByWeight(const int &w)
- @brief 得到与该关键帧连接的权重超过w的关键帧
- @param[in] w 权重阈值
- @return vector<KeyFrame*> 满足权重条件的关键帧向量
SetBadFlag()
- @brief 真正地执行删除关键帧的操作
- 需要删除的是该关键帧和其他所有帧、地图点之间的连接关系
- mbNotErase作用:表示要删除该关键帧及其连接关系但是这个关键帧有可能正在回环检测或者计算sim3操作,这时候虽然这个关键帧冗余,但是却不能删除,
- 仅设置mbNotErase为true,这时候调用setbadflag函数时,不会将这个关键帧删除,只会把mbTobeErase变成true,代表这个关键帧可以删除但不到时候,先记下来以后处理。
- 在闭环线程里调用 SetErase()会根据mbToBeErased 来删除之前可以删除还没删除的帧。
总的来说,就是删除当前关键帧所有的关系,并使得每一个子关键帧找到新的父关键帧
步骤:
- 处理删除不了的情况(第0关键帧不允许被删除;mbNotErase==true的不删除)
- 遍历所有和当前关键帧相连的关键帧,删除他们与当前关键帧的联系(即删除mConnectedKeyFrameWeights成员中的数据)
- 遍历每一个当前关键帧的地图点,删除每一个地图点和当前关键帧的联系。 清空自己与其他关键帧之间的联系
- 更新生成树,主要是处理好父子关键帧,不然会造成整个关键帧维护的图断裂,或者混乱。 首先将当前帧的父关键帧放入候选父关键帧 // 然后开始迭代,每迭代一次就为其中一个子关键帧寻找父关键帧(最高共视程度),找到父的子关键帧可以作为其他子关键帧的候选父关键帧
- 遍历每一个子关键帧,让它们更新它们指向的父关键帧
- 若该子关键帧无效,则跳过
- 得到与该子关键帧共视的关键帧
- 遍历每一个共视关键帧 for
- 遍历每一个当前关键帧的候选父关键帧
- 如果子关键帧的共视关键帧与待候选父关键帧有共视,则比较子关键帧与该共视关键帧的权重大小,选择权重最大的共视关键帧作为新的父关键帧
- 遍历每一个当前关键帧的候选父关键帧
- 如果在上面的过程找到了新的父节点,则更新结点关系(子关键帧获得新的父关键帧,然后该子节点升级,作为其他子节点的候选父节点,删除原关键帧中的该子节点信息);否之,退出循环。
- 遍历每一个子关键帧,让它们更新它们指向的父关键帧
- 如果还有子节点没有找到新的父节点
- 则直接把原关键帧的父节点作为自己的父节点
- 原关键帧的父关键帧删除该帧的信息
- 保留原父关键帧到当前关键帧的位姿变换,在保存位姿的时候使用
- 标记当前关键帧已经挂了
- 地图和关键帧数据库中删除该关键帧
KeyFrameDatabase.h
参数:
函数:
void KeyFrameDatabase::add(KeyFrame *pKF)
- @brief 数据库有新的关键帧,根据关键帧的词袋向量,更新数据库的倒排索引
- @param[in] pKF 新添加到数据库的关键帧
- 就是将倒排索引mvInveryedFile中的每一个与pKF有关的word id,都添加该关键帧

void KeyFrameDatabase::add(KeyFrame *pKF)
{
// 线程锁
unique_lock<mutex> lock(mMutex);
// 将该关键帧词袋向量里每一个单词更新倒排索引
for(DBoW2::BowVector::const_iterator vit= pKF->mBowVec.begin(), vend=pKF->mBowVec.end(); vit!=vend; vit++)
mvInvertedFile[vit->first].push_back(pKF);
}
倒排索引:有时也叫逆向索引,它是词袋模型中一个非常重要的概念。以单词为索引基础,存储有单词出现的所有图像的ID及对应的权重。倒排索引的优势是可以快速查询某个单词出现在哪些图像中,进而得到那些图像中有多少个共同的单词。这对判断图像的相似性非常有效。
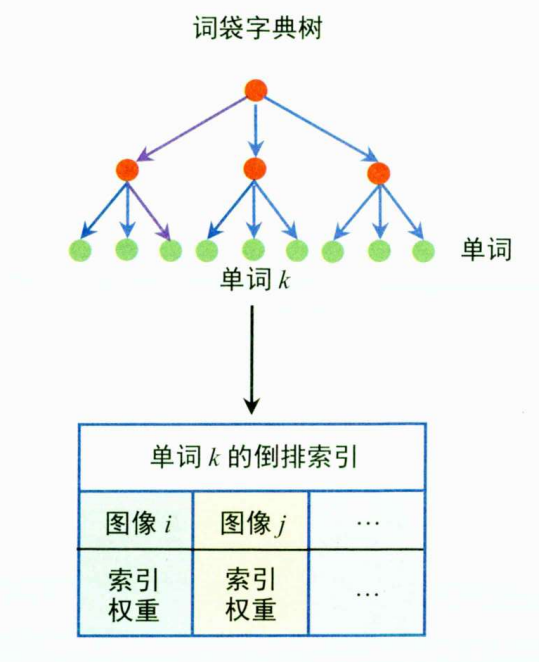
直接索引:以图像为索引基础,每张图像存储图像特征和该特征所在的节点ID。直接索引的优势是能够快速获取同一个节点下的所有特征点,加速不同图像之间的特征匹配和几何关系验证。

void KeyFrameDatabase::erase(KeyFrame* pKF)
- @brief 关键帧被删除后,更新数据库的倒排索引
- @param[in] pKF 删除的关键帧
步骤:
- 每一个KeyFrame包含多个words,
- 遍历mvInvertedFile中的这些words,
- 然后在word中删除该KeyFrame
void KeyFrameDatabase::erase(KeyFrame* pKF)
{
// 线程锁,保护共享数据
unique_lock<mutex> lock(mMutex);
// Erase elements in the Inverse File for the entry
// 每一个KeyFrame包含多个words,遍历mvInvertedFile中的这些words,然后在word中删除该KeyFrame
for(DBoW2::BowVector::const_iterator vit=pKF->mBowVec.begin(), vend=pKF->mBowVec.end(); vit!=vend; vit++)
{
// List of keyframes that share the word
// 取出包含该单词的所有关键帧列表
list<KeyFrame*> &lKFs = mvInvertedFile[vit->first];
// 如果包含待删除的关键帧,则把该关键帧从列表里删除
for(list<KeyFrame*>::iterator lit=lKFs.begin(), lend= lKFs.end(); lit!=lend; lit++)
{
if(pKF==*lit)
{
lKFs.erase(lit);
break;
}
}
}
}
vector<KeyFrame*> KeyFrameDatabase::DetectRelocalizationCandidates(Frame *F)
- @brief 在重定位中找到与该帧相似的候选关键帧组
- Step 1. 找出和当前帧具有公共单词的所有关键帧
- Step 2. 只和具有共同单词较多的关键帧进行相似度计算
- Step 3. 将与关键帧相连(权值最高)的前十个关键帧归为一组,计算累计得分
- Step 4. 只返回累计得分较高的组中分数最高的关键帧
- @param F 需要重定位的帧
- @return 相似的候选关键帧数组
步骤:
- 找出和当前帧具有公共单词(word)的所有关键帧
- 遍历BowVec(内部实际存储的是std::map<WordId, WordValue>) for
- 根据倒排索引找到每个wordID对应的所有关键帧,遍历关键帧列表 for
- 如果当前关键帧没有被标记过,则初始化,将当前帧标记为F的重定位候选帧,并保存
- pKFi->mnRelocWords++; (和那个要进行重定位的帧,所具有相同的单词的个数)
- 根据倒排索引找到每个wordID对应的所有关键帧,遍历关键帧列表 for
- 遍历BowVec(内部实际存储的是std::map<WordId, WordValue>) for
- 如果和当前帧具有公共单词的关键帧数目为0,无法进行重定位,返回空
- 统计上述关键帧中与当前帧F具有共同单词最多的单词数maxCommonWords,用来设定阈值1 。 (阈值1:最小公共单词数为最大公共单词数目的0.8倍)
- 遍历上述关键帧,挑选出共有单词数大于阈值1的及其和当前帧单词匹配得分存入lScoreAndMatch 。
- 计算lScoreAndMatch中每个关键帧的共视关键帧组的总得分,得到最高组得分bestAccScore,并以此决定阈值2 。单单计算当前帧和某一关键帧的相似性是不够的,这里将与关键帧共视程度最高的前十个关键帧归为一组,计算累计得分。
- 得到所有组中总得分大于阈值2的,组内得分最高的关键帧,作为候选关键帧组。(阈值2:最高得分的0.75倍)
vector<KeyFrame*> KeyFrameDatabase::DetectLoopCandidates(KeyFrame* pKF, float minScore)
- @brief 在闭环检测中找到与该关键帧可能闭环的关键帧(注意不和当前帧连接)
- Step 1:找出和当前帧具有公共单词的所有关键帧,不包括与当前帧连接的关键帧
- Step 2:只和具有共同单词较多的(最大数目的80%以上)关键帧进行相似度计算
- Step 3:计算上述候选帧对应的共视关键帧组的总得分,只取最高组得分75%以上的组
- Step 4:得到上述组中分数最高的关键帧作为闭环候选关键帧
- @param[in] pKF 需要闭环检测的关键帧
- @param[in] minScore 候选闭环关键帧帧和当前关键帧的BoW相似度至少要大于minScore
- @return vector<KeyFrame*> 闭环候选关键帧
步骤:
-
取出与当前关键帧相连(>15个共视地图点)的所有关键帧,这些相连关键帧都是局部相连,在闭环检测的时候将被剔除
-
创建
list<KeyFrame*> lKFsSharingWords;,用于保存可能与当前关键帧形成闭环的候选帧(只要有相同的word,且不属于局部相连(共视)帧) -
Step 1:找出和当前帧具有公共单词的所有关键帧,不包括与当前帧连接的关键帧
-
words是检测图像是否匹配的枢纽,遍历该pKF的每一个word,for
-
提取所有包含该word的KeyFrame
-
遍历上一步的关键帧,for
-
如果该帧没有被标记为当前帧的闭环候选关键帧,则
-
if(pKFi->mnLoopQuery!=pKF->mnId) { // 还没有标记为pKF的闭环候选帧 pKFi->mnLoopWords=0; // 和当前关键帧共视的话不作为闭环候选帧 if(!spConnectedKeyFrames.count(pKFi)) { // 没有共视就标记作为闭环候选关键帧,放到lKFsSharingWords里 pKFi->mnLoopQuery=pKF->mnId; lKFsSharingWords.push_back(pKFi); } } -
记录当前帧与关键帧具有相同word的个数
pKFi->mnLoopWords++;
-
-
-
-
-
如果没有关键帧和这个关键帧具有相同的单词,那么就返回空
-
Step 2:统计上述所有闭环候选帧中与当前帧具有共同单词最多的单词数,用来决定相对阈值
- 遍历所有闭环候选帧,找到最大单词数
maxCommonWords - 确定阈值最小公共单词数
minCommonWords为最大公共单词数maxCommonWords的0.8倍
- 遍历所有闭环候选帧,找到最大单词数
-
Step 3:遍历上述所有闭环候选帧,挑选出共有单词数大于
minCommonWords且单词匹配度大于minScore存入lScoreAndMatch- 遍历所有闭环候选帧,for
- 获取一个帧,pkfi
- 如果该帧pkfi的共同单词数>minCommonWords,则
- 用mBowVec计算该帧与当前关键帧之间相似度得分si,并保存到该帧中
- 如果si>预先设定的最小得分minScore,则将该帧存入lScoreAndMatch
- 遍历所有闭环候选帧,for
-
如果lScoreAndMatch为空,则
return vector<KeyFrame*>(); -
单单计算当前帧和某一关键帧的相似性是不够的,这里将与关键帧相连(权值最高,共视程度最高)的前十个关键帧归为一组,计算累计得分。
Step 4:计算上述候选帧对应的共视关键帧组的总得分,得到最高组得分bestAccScore,并以此决定阈值minScoreToRetain
- 遍历上述每个候选帧,for
- 获取当前候选帧的前10和最好共视关键帧
- 遍历所有共视关键帧,累计得分,for
- 如果当前共视关键帧也在当前关键帧的闭环候选帧,且公共单词数超过最小要求,则
- 累加得分
- 统计得到组里分数最高的关键帧pkf2,并记录
- 如果当前共视关键帧也在当前关键帧的闭环候选帧,且公共单词数超过最小要求,则
- 将累计得分和最高得分关键帧pkf2保存
- 记录所有组中组得分最高的组的得分,用于确定相对阈值
- 遍历上述每个候选帧,for
-
所有组中最高得分的0.75倍,作为最低阈值
-
Step 5:只取组得分大于阈值的组,得到组中分数最高的关键帧们作为闭环候选关键帧,(注意同一帧只取一次,避免重复添加)
LocalMapping.h
参数:
原理

函数:
void LocalMapping::ProcessNewKeyFrame()
- @brief 处理列表中的关键帧,包括计算BoW、更新观测、描述子、共视图,插入到地图等
- 局部建图线程中的关键帧来自跟踪线程。这些关键帧帧会进入一个队列中,等待局部建图线程的处理,包括计算词袋向量,更新观测、描述子、共视图,插入到地图中,具体流程如下。
步骤:
-
step 1:从缓冲队列中取出一帧关键帧,该关键帧队列是Tracking线程向LocaMapping中插入的关键帧组成
- 取出列表中最前面的关键帧,作为当前要处理的关键帧
- 取出最前面的关键帧后,在原来的列表里删掉该关键帧
-
step 2:计算该关键帧特征点的词袋向量
-
step 3:当前处理关键帧中有效的地图点,更新normal,描述子等信息
-
TrackLocalMap中和当前帧新匹配上的地图点和当前关键帧进行关联绑定(获取当前关键帧的所有地图点匹配)
-
对当前处理的这个关键帧中的所有的地图点展开遍历
-
获取当前地图点
-
判断当前点是否存在,如果存在,则继续
-
判断当前点是否为坏点,如果不是坏点,则继续
-
if 如果当前地图点没有被当前关键帧所观测到,说明该地图点不是来自当前帧的观测(比如来自局部地图点),则
-
为当前地图点添加观测
pMP->AddObservation(mpCurrentKeyFrame, i); -
获得该点的平均观测方向和观测距离范围
pMP->UpdateNormalAndDepth(); -
更新地图点的最佳描述子
pMP->ComputeDistinctiveDescriptors();
-
-
else 如果当前地图点被当前帧观测到,说明这些地图点可能来自双目或RGBD在创建关键帧中新生成的地图点,或者是CreateNewMapPoints 中通过三角化产生,则将上述地图点放入mlpRecentAddedMapPoints,等待后续MapPointCulling函数的检验
mlpRecentAddedMapPoints.push_back(pMP); -
Step 4:更新关键帧间的连接关系(共视图)
mpCurrentKeyFrame->UpdateConnections(); -
Step 5:将该关键帧插入到地图中
mpMap->AddKeyFrame(mpCurrentKeyFrame);
-
-
void LocalMapping::MapPointCulling()
- @brief 检查新增地图点,根据地图点的观测情况剔除质量不好的新增的地图点
- mlpRecentAddedMapPoints:存储新增的地图点,这里是要删除其中不靠谱的

步骤:
-
获取最近增加的地图点和当前帧的ID
-
step 1:根据相机类型设置不同的观测阈值
-
step 2:遍历检查新添加的地图点,while,当没有指向到最后时,一直循环
-
判断该点是否为坏点,如果是坏点,则(Step 2.1)将其从队列中删除
-
(Step 2.2)如果跟踪到该地图点的帧数相比预计可观测到该地图点的帧数的比例小于25%,则从地图中删除
// Step 2.2:跟踪到该地图点的帧数相比预计可观测到该地图点的帧数的比例小于25%,从地图中删除 // (mnFound/mnVisible) < 25% // mnFound :地图点被多少帧(包括普通帧)看到,次数越多越好 // mnVisible:地图点应该被看到的次数 // (mnFound/mnVisible):对于大FOV镜头这个比例会高,对于窄FOV镜头这个比例会低 pMP->SetBadFlag(); lit = mlpRecentAddedMapPoints.erase(lit); -
(Step 2.3:)如果从该点建立开始,到现在已经过了不小于2个关键帧,但是观测到该点的相机数却不超过阈值cnThObs,从地图中删除
pMP->SetBadFlag(); lit = mlpRecentAddedMapPoints.erase(lit); -
(Step 2.4)如果从建立该点开始,已经过了3个关键帧而没有被剔除,则认为是质量高的点,因此没有SetBadFlag(),仅从队列中删除
lit = mlpRecentAddedMapPoints.erase(lit); -
如果上面的判断都不成立,则lit++,指向下一个点
-
void LocalMapping::CreateNewMapPoints()
- @brief 用当前关键帧与相邻关键帧通过三角化产生新的地图点,使得跟踪更稳
步骤:
-
不同传感器下对搜索最佳共视关键帧的数目(用nn表示)不同,单目的收需要有更多的具有较好共视关系的关键帧来建立地图
-
step 1 :在当前关键帧的共视关键帧中找到共视程度最高的nn帧相邻关键帧
- 获取当前关键帧的前nn个共视程度最高的帧
- 特征点匹配配置,最佳距离 < 0.6 * 次佳距离 ,比较苛刻了。不检查旋转。
- 取出当前帧从世界坐标系到相机坐标系的变换矩阵
- 得到当前关键帧(左目)光心在世界坐标系中的坐标、内参
-
Step 2:遍历相邻关键帧,搜索匹配并用极线约束剔除误匹配,最终三角化,for,以一个帧为例
-
如果i>0且列表中有待插入的关键帧,则退出return。(这里是因为下面的过程会比较耗费时间,因此如果有新的关键帧需要处理,就暂时退出)
-
获取相邻关键帧
-
获取相邻关键光心在世界坐标系中的坐标
-
计算基线相邻,即两个关键帧间的相机位移
-
计算基线长度
-
Step 3:判断相机运动的基线是不是足够长
- 如果不是单目相机,是双目相机时,关键帧间距小于本身的基线时不生成3D点,因为太短的基线下是能够恢复的地图点不稳定
- 如果是单目相机,则
- 评估当前相邻关键帧的场景深度中值
- 计算基线与深读中值的比例
- 如果比例特别小,则认为关键帧之间的基线太小,恢复的3D点不准确,那么跳过当前邻接的关键帧,不生成3D点
-
Step 4 :根据两个关键帧直接的位姿计算它们之间的基础矩阵
-
Step 5 :通过词袋对量关键帧的未匹配的特征点快速匹配,用极线约束抑制离群点,生成新的匹配对
-
获取当前相邻关键帧的旋转矩阵、平移矩阵、相机内参
-
Step 6:对每对匹配通过三角化生成3D点,和 Triangulate函数差不多,遍历每个匹配,for
-
step 6.1取出匹配特征点
- 获取当前匹配对在当前关键帧中的索引
- 获取当前匹配对在邻接关键帧中的索引
- 获取当前匹配在当前关键帧中的特征点
- 判断该点是否为双目(mvuRight中存放着双目的深度值,如果不是双目,其值将为-1)
- 获取当前匹配在相邻关键帧中的特征点,并判断该点是否为双目
-
Step 6.2:利用匹配点反投影得到视差角,特征点反投影,其实得到的是在各自相机坐标系下的一个非归一化的方向向量,和这个点的反投影射线重合
- 将两个特征点的坐标进行归一化处理
- 由相机坐标系转到世界坐标系(得到的是那条反投影射线的一个同向向量在世界坐标系下的表示,还是只能够表示方向),得到视差角余弦值
- 加1是为了让cosParallaxStereo随便初始化为一个很大的值
-
Step 6.3:对于双目,利用双目得到视差角;单目相机没有特殊操作
- 如果当前关键帧的特征点对应的传感器是双目,并且当前的关键帧的这个点有对应的深度,则假设是平行的双目相机,计算出双目相机观察这个点的时候的视差角余弦
- 否则,如果相邻关键帧的特征点对应的传感器是双目,则和上面一样
-
Step 6.4:三角化恢复3D点
// cosParallaxRays>0 && (bStereo1 || bStereo2 || cosParallaxRays<0.9998)表明视差角正常,0.9998 对应1° // cosParallaxRays < cosParallaxStereo 表明匹配点对夹角大于双目本身观察三维点夹角 // 匹配点对夹角大,用三角法恢复3D点 // 参考:https://github.com/raulmur/ORB_SLAM2/issues/345-
如果匹配点夹角大,则使用三角法恢复3D点。
见Initializer.cc的 Triangulate 函数,实现是一样的,顶多就是把投影矩阵换成了变换矩阵
-
否则,如果匹配点对夹角小,用双目恢复3D点,用视差角更大的那个双目信息来恢复,直接用已知3D点反投影了
-
否则,如果没有双目,且视角非常低,则放弃
-
-
Step 6.5:检测生成的3D点是否在相机前方,不在的话就放弃这个点
-
Step 6.6:计算3D点在当前关键帧下的重投影误差(这里分别对两个帧都进行投影,计算重投影误差)
- 计算3D点在相机坐标系下的坐标
- 如果是单目情况,则直接根据内参投影到像素平面,并与特征点计算误差,判断卡方检验阈值(自由度为2),若不满足,则continue,处理下一个点
- 如果是双目情况,则还需要根据视差公式计算假想的右目坐标,然后计算误差,判断卡方检验阈值(自由度为3),若不满足,则continue,处理下一个点
-
Step 6.7:检查尺度连续性
- 世界坐标系下,3D点与相机间的向量,方向由相机指向3D点
- 距离的比例和图像金字塔的比例不应该差太多,否则就跳过
-
Step 6.8:三角化生成3D点成功,构造成MapPoint
-
Step 6.9:为该MapPoint添加属性:
- 观测到该MapPoint的关键帧
- 该MapPoint的描述子
- 该MapPoint的平均观测方向和深度范围
-
Step 6.10:将新产生的点放入检测队列,这些MapPoints都会经过MapPointCulling函数的检验
-
-
cv::Mat LocalMapping::ComputeF12(KeyFrame *&pKF1, KeyFrame *&pKF2)
-
根据两关键帧的姿态计算两个关键帧之间的基本矩阵

cv::Mat LocalMapping::ComputeF12(KeyFrame *&pKF1, KeyFrame *&pKF2)
{
// 先构造两帧之间的R12,t12
cv::Mat R1w = pKF1->GetRotation();
cv::Mat t1w = pKF1->GetTranslation();
cv::Mat R2w = pKF2->GetRotation();
cv::Mat t2w = pKF2->GetTranslation();
cv::Mat R12 = R1w*R2w.t();
cv::Mat t12 = -R1w*R2w.t()*t2w+t1w;
// 得到 t12 的反对称矩阵
cv::Mat t12x = SkewSymmetricMatrix(t12);
const cv::Mat &K1 = pKF1->mK;
const cv::Mat &K2 = pKF2->mK;
// Essential Matrix: t12叉乘R12
// Fundamental Matrix: inv(K1)*E*inv(K2)
return K1.t().inv()*t12x*R12*K2.inv();
}
void LocalMapping::SearchInNeighbors()
-
@brief 检查并融合当前关键帧与相邻帧(两级相邻)重复的地图点
-


步骤:
-
Step 1:获得当前关键帧在共视图中权重排名前nn的邻接关键帧。单目情况要20个邻接关键帧,双目或者RGBD则要10个。
开始之前先定义几个概念:当前关键帧的邻接关键帧,称为一级相邻关键帧,也就是邻居;与一级相邻关键帧相邻的关键帧,称为二级相邻关键帧,也就是邻居的邻居。
-
Step 2:存储一级相邻关键帧及其二级相邻关键帧,对所有候选的一级关键帧展开遍历,for
- 获取一个帧
- 如果该帧是坏的或者其与当前帧进行过融合操作,则跳过该帧,continue
- 存储该一级相邻关键帧,并将其标记
- 找到并以一级相邻关键帧的共视关系最好的5个相邻关键帧作为二级相邻关键帧
- 遍历所有的二级关键帧,for
- 如果该帧是坏点或者该帧与当前关键帧帧发生过融合,则跳过该帧,continue
- 存储该二级相邻关键帧,并将其标记
-
构造ORBmather类型的变量,使用默认参数,最优和次优比例0.6,匹配时检查特征点的旋转
-
Step 3:将当前帧的地图点分别投影到两级相邻关键帧,寻找匹配点对应的地图点进行融合,称为正向投影融合
- 获取当前帧的所有地图点
- 遍历每一个相邻关键帧,for
- 获关键帧
- 将地图点投影到关键帧中进行匹配和融合,融合策略如下:
- 如果地图点能匹配关键帧的特征点,并且该点有对应的地图点,那么选择观测数目多的替换两个地图点
- 如果地图点能匹配关键帧的特征点,并且该点没有对应的地图点,那么为该点添加该投影地图点
- 注意这个时候对地图点融合的操作是立即生效的
- 整个流程使用的函数为
matcher.Fuse(pKFi,vpMapPointMatches);
-
Step 4:将两级相邻关键帧地图点分别投影到当前关键帧,寻找匹配点对应的地图点进行融合,称为反向投影融合
vector<MapPoint*> vpFuseCandidates;用于进行存储要融合的一级邻接和二级邻接关键帧所有MapPoints的集合- Step 4.1:遍历每一个一级邻接和二级邻接关键帧,收集他们的地图点存储到 vpFuseCandidates,for
- 获取相邻帧,并获取该帧对应的所有地图点
- 遍历上一步的所有地图点,找出需要进行融合的并且加入到集合中,for
- 如果该点不存在,则continue,跳过该点
- 如果该地图点时坏点或者该地图点已经加入到集合中,则continue,跳过该点
- 将该点加入集合,并标记已经加入
- Step 4.2:进行地图点投影融合,和正向融合操作是完全相同的。不同的是正向操作是"每个关键帧和当前关键帧的地图点进行融合",而这里的是"当前关键帧和所有邻接关键帧的地图点进行融合"
matcher.Fuse(mpCurrentKeyFrame,vpFuseCandidates);
- Step 4.1:遍历每一个一级邻接和二级邻接关键帧,收集他们的地图点存储到 vpFuseCandidates,for
-
Step 5:更新当前帧地图点的描述子、深度、平均观测方向等属性
-
获取当前关键帧的所有地图点
-
遍历每一个地图点,for
-
如果该点存在,则
-
如果该点不是坏点,则
-
在所有找到pMP的关键帧中,获得最佳的描述子
pMP->ComputeDistinctiveDescriptors(); -
更新平均观测方向和观测距离
pMP->UpdateNormalAndDepth();
-
-
-
-
-
Step 6:更新当前帧与其它帧的共视连接关系
mpCurrentKeyFrame->UpdateConnections();
void LocalMapping::KeyFrameCulling()
-
@brief 检测当前关键帧在共视图中的关键帧,根据地图点在共视图中的冗余程度剔除该共视关键帧
-
冗余关键帧的判定:90%以上的地图点能被其他关键帧(至少3个)观测到
-


-
// 该函数里变量层层深入,这里列一下: // mpCurrentKeyFrame:当前关键帧,本程序就是判断它是否需要删除 // pKF: mpCurrentKeyFrame的某一个共视关键帧 // vpMapPoints:pKF对应的所有地图点 // pMP:vpMapPoints中的某个地图点 // observations:所有能观测到pMP的关键帧 // pKFi:observations中的某个关键帧 // scaleLeveli:pKFi的金字塔尺度 // scaleLevel:pKF的金字塔尺度
步骤
-
step 1 :根据共视图提取当前关键帧的所有共视关键帧
-
获取当前帧的所有共视关键帧
-
对所有的共视关键帧进行遍历,for
-
如果该共视关键帧帧是第一个关键帧,则跳过,continue,因为第一个关键帧不能删除
-
step 2:提取每个共视关键帧的地图点
-
step 3:遍历该共视关键帧的所有地图点,其中能被其它至少3个关键帧观测到的地图点为冗余地图点,for
-
如果该点存在,则继续下一步
-
如果该点不是坏点,则继续下一步
-
如果是双目或者RGB-D,则仅考虑近处(不超过基线的40倍)的地图点
-
如果该点被观测到的次数大于观测阈值,则继续下一步
-
获取该地图点在共视关键帧中金字塔的层数
const int &scaleLevel = pKF->mvKeysUn[i].octave; -
获取能看到该地图点的所有关键帧集合
-
遍历观测到该地图点的关键帧,for
-
如果该帧与共视关键帧相同,则跳过continue
-
获取地图点在该帧投影的金字塔层数
const int &scaleLeveli = pKFi->mvKeysUn[mit->second].octave; -
如果scaleLeveli<=scaleLevel + 1
if(scaleLeveli<=scaleLevel+1) { nObs++; // 已经找到3个满足条件的关键帧,就停止不找了 if(nObs>=thObs) break; }
-
-
地图点至少被3个关键帧观测到,就记录为冗余点,更新冗余点计数数目
-
-
step 4:如果该关键帧90%以上的有效地图点被判断为冗余的,则认为该关键帧是冗余的,需要删除该关键帧
-
-
void LocalMapping::Run()
- 线程主函数
步骤:
-
标记状态,表示当前run函数正在运行,尚未结束
-
主循环,while(1)
-
Step 1 告诉Tracking,LocalMapping正处于繁忙状态,请不要给我发送关键帧打扰我。LocalMapping线程处理的关键帧都是Tracking线程发来的。
SetAcceptKeyFrames(false); -
如果等待处理的关键帧列表不为空,则
-
Step 2 处理列表中的关键帧,包括计算BoW、更新观测、描述子、共视图,插入到地图等
ProcessNewKeyFrame(); -
Step 3 根据地图点的观测情况剔除质量不好的地图点
MapPointCulling(); -
Step 4 当前关键帧与相邻关键帧通过三角化产生新的地图点,使得跟踪更稳
CreateNewMapPoints(); -
如果已经处理完队列中的最后一个关键帧,则
- step 5 检查并融合当前关键帧与相邻关键帧(两级相邻)中重复的地图点
-
如果已经处理完队列中的最后一个关键帧,并且闭环检测没有请求停止LocalMapping,则
-
step 6 当局部地图中的关键帧大于2个的时候进行局部地图的BA
-
step 7 检测并提出当前帧相邻的关键帧中冗余的关键帧。
冗余的判定:该关键帧的90%的地图点可以被其他关键帧观测到
KeyFrameCulling();
-
-
Step 8 将当前帧加入到闭环检测队列中,注意这里的关键帧被设置成为了bad的情况,这个需要注意
mpLoopCloser->InsertKeyFrame(mpCurrentKeyFrame);
-
-
否则,如果等待处理的关键帧列表 为空且要终止当前线程,则
-
// Safe area to stop while(isStopped() && !CheckFinish()) { // 如果还没有结束利索,那么等 // usleep(3000); std::this_thread::sleep_for(std::chrono::milliseconds(3)); } // 然后确定终止了就跳出这个线程的主循环 if(CheckFinish()) break;
-
-
查看是否有复位线程的请求
-
设置“允许接受关键帧”的状态标志
-
如果当前线程已经结束了就跳出主循环
-
usleep(3000);
-
-
设置线程已经终止
SetFinish();
LoopClosing.h
参数:
函数:
bool LoopClosing::DetectLoop()
- @brief 闭环检测
- @return true 成功检测到闭环
- @return false 未检测到闭环
步骤:
-
step 1 从队列中取出一个关键帧,作为当前检测闭环关键帧
- 从队列头开始取,也就是先取早进来的关键帧
- 取出关键帧后从队列里弹出该关键帧
- 设置当前关键帧不要再优化的过程中被删除
-
step 2 如果距离上次闭环没多久(小于10帧),或者map中关键帧总共还没有10帧,则不进行闭环检测
if(mpCurrentKF->mnId<mLastLoopKFid+10) { mpKeyFrameDB->add(mpCurrentKF); mpCurrentKF->SetErase(); return false; } -
Step 3:遍历当前回环关键帧所有连接(>15个共视地图点)关键帧,计算当前关键帧与每个共视关键的bow相似度得分,并得到最低得分minScore
- 得到所有与当前帧相连的关键帧
- 获取当前帧的BowVec向量
- 遍历所有相连的帧,for
- 如果该帧是坏的,则跳过该帧,continue
- 获取该帧的BowVec向量
- 计算两帧的相似度得分,得分越低,相似度越低
- 更新最低得分minScore
-
step 4 在所有关键帧中找出闭环关键帧(注意不和当前帧连接)。
-
minScore的作用:认为和当前关键帧具有回环关系的关键帧,不应该低于当前关键帧的相邻关键帧的最低的相似度minScore。得到的这些关键帧,和当前关键帧具有较多的公共单词,并且相似度评分都挺高。
vector<KeyFrame*> vpCandidateKFs = mpKeyFrameDB->DetectLoopCandidates(mpCurrentKF, minScore); -
如果没有闭环关键帧,则返回false
-
-
step 5 在候选帧中检测具有连续性的候选帧
// Step 5:在候选帧中检测具有连续性的候选帧 // 1、每个候选帧将与自己相连的关键帧构成一个“子候选组spCandidateGroup”, vpCandidateKFs-->spCandidateGroup // 2、检测“子候选组”中每一个关键帧是否存在于“连续组”,如果存在 nCurrentConsistency++,则将该“子候选组”放入“当前连续组vCurrentConsistentGroups” // 3、如果nCurrentConsistency大于等于3,那么该”子候选组“代表的候选帧过关,进入mvpEnoughConsistentCandidates // 相关的概念说明:(为方便理解,见视频里的图示) // 组(group): 对于某个关键帧, 其和其具有共视关系的关键帧组成了一个"组"; // 子候选组(CandidateGroup): 对于某个候选的回环关键帧, 其和其具有共视关系的关键帧组成的一个"组"; // 连续(Consistent): 不同的组之间如果共同拥有一个及以上的关键帧,那么称这两个组之间具有连续关系 // 连续性(Consistency):称之为连续长度可能更合适,表示累计的连续的链的长度:A--B 为1, A--B--C--D 为3等;具体反映在数据类型 ConsistentGroup.second上 // 连续组(Consistent group): mvConsistentGroups存储了上次执行回环检测时, 新的被检测出来的具有连续性的多个组的集合.由于组之间的连续关系是个网状结构,因此可能存在 // 一个组因为和不同的连续组链都具有连续关系,而被添加两次的情况(当然连续性度量是不相同的) // 连续组链:自造的称呼,类似于菊花链A--B--C--D这样形成了一条连续组链.对于这个例子中,由于可能E,F都和D有连续关系,因此连续组链会产生分叉;为了简化计算,连续组中将只会保存 // 最后形成连续关系的连续组们(见下面的连续组的更新) // 子连续组: 上面的连续组中的一个组 // 连续组的初始值: 在遍历某个候选帧的过程中,如果该子候选组没有能够和任何一个上次的子连续组产生连续关系,那么就将添加自己组为连续组,并且连续性为0(相当于新开了一个连续链) // 连续组的更新: 当前次回环检测过程中,所有被检测到和之前的连续组链有连续的关系的组,都将在对应的连续组链后面+1,这些子候选组(可能有重复,见上)都将会成为新的连续组; // 换而言之连续组mvConsistentGroups中只保存连续组链中末尾的组 //最终筛选后得到的闭环帧-
遍历刚才得到的每一个候选关键帧,for
-
获取一个候选关键帧
-
step 5.2 将自己以及与自己相连的关键帧构成一个“子候选组”。注意:要把自己加进去
-
Step 5.3:遍历前一次闭环检测到的连续组链。
上一次闭环的连续组链 ,for
std::vector<ConsistentGroup> mvConsistentGroups其中ConsistentGroup的定义:typedef pair<set<KeyFrame*>,int> ConsistentGroup其中 ConsistentGroup.first对应每个“连续组”中的关键帧集合,ConsistentGroup.second为每个“连续组”的连续长度-
取出之前的一个子连续组中的关键帧集合
-
step 5.4 遍历每个“子候选组”,检测子候选组中每一个关键帧在“子连续组”中是否存在。如果有一帧共同存在于“子候选组”与之前的“子连续组”,那么“子候选组”与该“子连续组”连续
-
Step 5.5:如果判定为连续,接下来判断是否达到连续的条件
-
取出和当前的候选组发生"连续"关系的子连续组的"已连续次数"
-
将当前候选组连续长度在原子连续组的基础上 +1
-
如果上述连续关系还未记录到 vCurrentConsistentGroups,那么记录一下,如下。(注意这里spCandidateGroup 可能放置在vbConsistentGroup中其他索引(iG)下)
- 将该“子候选组”的该关键帧打上连续编号加入到“当前连续组”
- 放入本次闭环检测的连续组vCurrentConsistentGroups里
- 标记一下,防止重复添加到同一个索引iG。但是spCandidateGroup可能重复添加到不同的索引iG对应的vbConsistentGroup 中
-
如果连续长度满足要求,那么当前的这个候选关键帧是足够靠谱的。
连续性阈值 mnCovisibilityConsistencyTh=3
足够连续的标记 bEnoughConsistent
-
-
-
Step 5.6:如果该“子候选组”的所有关键帧都和上次闭环无关(不连续),vCurrentConsistentGroups 没有新添加连续关系。于是就把“子候选组”全部拷贝到 vCurrentConsistentGroups, 用于更新mvConsistentGroups,连续性计数器设为0
-
-
更新连续组
-
当前闭环检测的关键帧添加到数据库中
-
如果未检测到闭环,则当前帧设置为可删除,返回false
-
如果检测到闭环,则返回true。
-
-
return false;
bool LoopClosing::ComputeSim3()
- @brief 计算当前关键帧和上一步闭环候选帧的Sim3变换
-
- 遍历闭环候选帧集,筛选出与当前帧的匹配特征点数大于20的候选帧集合,并为每一个候选帧构造一个Sim3Solver
-
- 对每一个候选帧进行 Sim3Solver 迭代匹配,直到有一个候选帧匹配成功,或者全部失败
-
- 取出闭环匹配上关键帧的相连关键帧,得到它们的地图点放入 mvpLoopMapPoints
-
- 将闭环匹配上关键帧以及相连关键帧的地图点投影到当前关键帧进行投影匹配
-
- 判断当前帧与检测出的所有闭环关键帧是否有足够多的地图点匹配
-
- 清空mvpEnoughConsistentCandidates
- @return true 只要有一个候选关键帧通过Sim3的求解与优化,就返回true
- @return false 所有候选关键帧与当前关键帧都没有有效Sim3变换
Sim3 计算流程说明:
- 通过Bow加速描述子的匹配,利用RANSAC粗略地计算出当前帧与闭环帧的Sim3(当前帧—闭环帧)
- 根据估计的Sim3,对3D点进行投影找到更多匹配,通过优化的方法计算更精确的Sim3(当前帧—闭环帧)
- 将闭环帧以及闭环帧相连的关键帧的地图点与当前帧的点进行匹配(当前帧—闭环帧+相连关键帧)
// 注意以上匹配的结果均都存在成员变量mvpCurrentMatchedPoints中,实际的更新步骤见CorrectLoop()步骤3
// 对于双目或者是RGBD输入的情况,计算得到的尺度=1
步骤:
-
准备工作
- 对每个(上一步得到的具有足够连续关系的)闭环候选帧都准备算一个Sim3
- 构建所需要的变量和参数
-
step 1 遍历闭环候选帧集,初步筛选出与当前关键帧的匹配特征点数大于20的候选帧集合,并为每一个候选帧构造一个Sim3Solver
开始遍历候选帧集,for
-
step 1.1 从筛选的闭环候选帧中取出一帧有效的关键帧pKF
- 获取该帧
- 将该帧设置为不可被剔除,避免在LocalMapping中KeyFrameCulling函数将此关键帧作为冗余帧剔除
- 如果该帧是质量不高,则放弃该帧,continue
-
step 1.2 将当前帧 mpCurrentKF 与闭环候选关键帧pKF匹配。通过bow加速得到 mpCurrentKF 与 pKF 之间的匹配特征点。vvpMapPointMatches 是匹配特征点对应的地图点,本质上来自于候选闭环帧
-
使用SearchByBoW函数获得当前帧与闭环候选关键帧之间的匹配关系
int nmatches = matcher.SearchByBoW(mpCurrentKF,pKF,vvpMapPointMatches[i]); -
进行粗筛,若匹配的特征点数太少,则将该候选帧剔除,continue
-
否则,
-
step 1.3 为保留的后询证构造Sim3求解器。如果 mbFixScale(是否固定尺度) 为 true,则是6 自由度优化(双目 RGBD);如果是false,则是7 自由度优化(单目)
-
Sim3Solver* pSolver = new Sim3Solver(mpCurrentKF,pKF,vvpMapPointMatches[i],mbFixScale); // Sim3Solver Ransac 过程置信度0.99,至少20个inliers 最多300次迭代 pSolver->SetRansacParameters(0.99,20,300); vpSim3Solvers[i] = pSolver;
-
-
记录保留的候选帧数量
-
-
-
step 2 对每一个候选帧用Sim3Solver 迭代匹配,直到有一个候选帧匹配成功,或者全部失败,
whlie(nCandidates>0 && !bMatch)-
遍历每一个候选帧,for
-
如果该帧被标记为放弃,则跳过,continue
-
获取该候选帧
-
构建变量:
- 内点(Inliers)标志,即标记经过RANSAC sim3 求解后,vvpMapPointMatches中的哪些作为内点。
vector<bool> vbInliers; - 内点(Inliers)数量。
int nInliers; - 是否到达了最优解。
bool bNoMore;
- 内点(Inliers)标志,即标记经过RANSAC sim3 求解后,vvpMapPointMatches中的哪些作为内点。
-
step 2.1 取出从 step 1.3 中为当前候选帧构建的Sim3Solver 并开始迭代
-
取出为当前候选帧的构建的Sim3Solver
-
开始迭代,设置最大迭代次数为5次,返回的Scm是候选帧PKF到当前帧mpCurrentKF的Sim3变换(T12)
cv::Mat Scm = pSolver->iterate(5,bNoMore,vbInliers,nInliers); -
如果总迭代次数达到最大限制还没有求出合格的Sim3变换,该候选帧剔除
-
-
如果Scm不为空,说明计算处理Sim3变换,则继续匹配出更多点并优化。因为之前SearchByBow 匹配可能会有遗漏。具体如下
-
取出当前候选帧经过Sim3Solver 操作后匹配点中的内点集合
-
Step 2.2 通过上面求取的Sim3变换引导关键帧匹配,弥补Step 1中的漏匹配
-
获取候选帧pKF到当前帧mpCurrentKF的R(R12),t(t12),变换尺度s(s12)
cv::Mat R = pSolver->GetEstimatedRotation(); cv::Mat t = pSolver->GetEstimatedTranslation(); const float s = pSolver->GetEstimatedScale(); -
// 查找更多的匹配(成功的闭环匹配需要满足足够多的匹配特征点数,之前使用SearchByBoW进行特征点匹配时会有漏匹配) // 通过Sim3变换,投影搜索pKF1的特征点在pKF2中的匹配,同理,投影搜索pKF2的特征点在pKF1中的匹配 // 只有互相都成功匹配的才认为是可靠的匹配 matcher.SearchBySim3(mpCurrentKF,pKF,vpMapPointMatches,s,R,t,7.5);
-
-
Step 2.3 用新的匹配来优化 Sim3,只要有一个候选帧通过Sim3的求解与优化,就跳出停止对其它候选帧的判断
// OpenCV的Mat矩阵转成Eigen的Matrix类型 // gScm:候选关键帧到当前帧的Sim3变换 g2o::Sim3 gScm(Converter::toMatrix3d(R),Converter::toVector3d(t),s); // 如果mbFixScale为true,则是6 自由度优化(双目 RGBD),如果是false,则是7 自由度优化(单目) // 优化mpCurrentKF与pKF对应的MapPoints间的Sim3,得到优化后的量gScm const int nInliers = Optimizer::OptimizeSim3(mpCurrentKF, pKF, vpMapPointMatches, gScm, 10, mbFixScale); -
如果优化成功(nInliers>=20),则停止while循环遍历闭环候选
if(nInliers>=20) { // 为True时将不再进入 while循环 bMatch = true; // mpMatchedKF就是最终闭环检测出来与当前帧形成闭环的关键帧 mpMatchedKF = pKF; // gSmw:从世界坐标系 w 到该候选帧 m 的Sim3变换,都在一个坐标系下,所以尺度 Scale=1 g2o::Sim3 gSmw(Converter::toMatrix3d(pKF->GetRotation()),Converter::toVector3d(pKF->GetTranslation()),1.0); // 得到g2o优化后从世界坐标系到当前帧的Sim3变换 mg2oScw = gScm*gSmw; mScw = Converter::toCvMat(mg2oScw); mvpCurrentMatchedPoints = vpMapPointMatches; // 只要有一个候选帧通过Sim3的求解与优化,就跳出停止对其它候选帧的判断 break; }
-
-
-
-
退出上面while循环的原因有两种,一种是求解到了BMatch置位后出的,另外一种是nCandidates耗尽为0
-
如果没有一个闭环匹配候选帧通过Sim3 的求解与优化,则清空mvpEnoughConsistentCandidates,这些候选关键帧以后都不会在再参加回环检测过程了,当前关键帧也将不会再参加回环检测了,Sim3 计算失败,退出了。
return false; -
Step 3:取出与当前帧闭环匹配上的关键帧及其共视关键帧,以及这些共视关键帧的地图点
// 注意是闭环检测出来与当前帧形成闭环的关键帧 mpMatchedKF // 将mpMatchedKF共视的关键帧全部取出来放入 vpLoopConnectedKFs // 将vpLoopConnectedKFs的地图点取出来放入mvpLoopMapPoints- 获取闭环关键帧的所有共视关键帧放入vpLoopConnectedKFs
- 将该闭环关键帧也放入vpLoopConnectedKFs,形成一个“闭环关键帧小组”
- 遍历这个组中的每一个关键帧,for
- 获取一个关键帧
- 获取该帧的所有地图点
- 遍历该帧的所有有效地图点,for
- 如果地图点存在,则
- 如果地图点不是坏点,且没有被当前帧标记,则将该点存入mvpLoopMapPoints,并标记该地图点
- 如果地图点存在,则
-
Step 4:将闭环关键帧及其连接关键帧的所有地图点投影到当前关键帧进行投影匹配
// 根据投影查找更多的匹配(成功的闭环匹配需要满足足够多的匹配特征点数) // 根据Sim3变换,将每个mvpLoopMapPoints投影到mpCurrentKF上,搜索新的匹配对 // mvpCurrentMatchedPoints是前面经过SearchBySim3得到的已经匹配的点对,这里就忽略不再匹配了 // 搜索范围系数为10 matcher.SearchByProjection(mpCurrentKF, mScw, mvpLoopMapPoints, mvpCurrentMatchedPoints,10); -
Step 5: 统计当前帧与闭环关键帧的匹配地图点数目,超过40个说明成功闭环,否则失败
- 统计成功匹配的地图点数目
- 如果超过40个,说明成功闭环,当前回环可靠,则保留当前待闭环关键帧,其他闭环候选全部删掉以后不用了,返回true
- 否则,说明闭环不可靠,闭环候选及当前待闭环帧全部删除,返回false
void LoopClosing::CorrectLoop()
-
@brief 闭环矫正
-
- 通过求解的Sim3以及相对姿态关系,调整与当前帧相连的关键帧位姿以及这些关键帧观测到的地图点位置(相连关键帧—当前帧)
-
- 将闭环帧以及闭环帧相连的关键帧的地图点和与当前帧相连的关键帧的点进行匹配(当前帧+相连关键帧—闭环帧+相连关键帧)
-
- 通过MapPoints的匹配关系更新这些帧之间的连接关系,即更新covisibility graph
-
- 对Essential Graph(Pose Graph)进行优化,MapPoints的位置则根据优化后的位姿做相对应的调整
-
- 创建线程进行全局Bundle Adjustment
-
// Step 0:结束局部地图线程、全局BA,为闭环矫正做准备 // Step 1:根据共视关系更新当前帧与其它关键帧之间的连接 // Step 2:通过位姿传播,得到Sim3优化后,与当前帧相连的关键帧的位姿,以及它们的MapPoints // Step 3:检查当前帧的MapPoints与闭环匹配帧的MapPoints是否存在冲突,对冲突的MapPoints进行替换或填补 // Step 4:通过将闭环时相连关键帧的mvpLoopMapPoints投影到这些关键帧中,进行MapPoints检查与替换 // Step 5:更新当前关键帧之间的共视相连关系,得到因闭环时MapPoints融合而新得到的连接关系 // Step 6:进行EssentialGraph优化,LoopConnections是形成闭环后新生成的连接关系,不包括步骤7中当前帧与闭环匹配帧之间的连接关系 // Step 7:添加当前帧与闭环匹配帧之间的边(这个连接关系不优化) // Step 8:新建一个线程用于全局BA优化 // g2oSic: 当前关键帧 mpCurrentKF 到其共视关键帧 pKFi 的Sim3 相对变换 // mg2oScw: 世界坐标系到当前关键帧的 Sim3 变换 // g2oCorrectedSiw:世界坐标系到当前关键帧共视关键帧的Sim3 变换
步骤:
-
step 0 结束局部地图线程、全局BA、为闭环矫正做准备
-
请求局部地图停止,防止回环矫正时局部地图线程中InsertKeyFrame函数插入新的管阿金真
-
如果全局BA在运行,则将其终止掉,迎接新的全局BA
-
一直等到局部地图线程结束在继续
while(!mpLocalMapper->isStopped()) { std::this_thread::sleep_for(std::chrono::milliseconds(1)); }
-
-
step 1 根据共视关系,更新当前关键帧与其他关键帧之间的连接关系。因为之前闭环检测、计算Sim3中改变了该关键帧的地图点,所以需要更新。
mpCurrentKF->UpdateConnections() -
step 2 通过位姿传播,得到Sim3 优化后,与当前帧相连的关键帧的位姿,以及它们的地图点。
当前帧与世界坐标系之间的Sim变换在ComputeSim函数中已经确定(在ComputeSim中通过候选关键帧到按当前帧的Sim3变换gScm和从世界坐标系到候选关键帧的Sim3变换gSmw得到经过g2o优化后世界坐标系到当前帧的Sim3变换)
通过相对位姿关系,可以确定这些相连的关键帧与世界坐标系之间的Sim3变换
-
取出当前关键帧及其共视关键帧,将其放在一起,称为“当前关键帧组”
-
创建变量CorrectedSim3、NonCorrectedSim3
CorrectedSim3存放闭环g2o优化后当前关键帧的共视关键帧的世界坐标系下Sim3变换
NonCorrectedSim3存放没有矫正的当前关键帧的共视关键帧的坐标系下Sim3变换
-
先将mpCurrentKF的Sim3 变换存入,认为是准的,所以固定不动。(mg2oScw是由ComputeSim函数中计算Sim3变换和优化后得到的。)
CorrectedSim3[mpcurrectKF]=mg2oScw -
获取当前关键帧到世界坐标系下的变换矩阵
cv::Mat Twc = mpCurrentKF->GetPoseInverse(); -
对地图点进行操作
-
锁定地图点
-
step 2.1 通过mg2oScw(认为是准的)来进行位姿传播,得到当前关键帧的共视关键帧的世界坐标系下的Sim3位姿 (矫正Sim3变换其实就是以当前帧为一个踏板,因为其Sim3变换是优化后的,根据其和相对关系得到的Sim3变换,更加的准确)
遍历“当前关键帧组”,for
-
获取当前帧pKFi的位姿Tiw
-
如果该帧为当前关键帧,则跳过,因为当前关键帧的位姿已经在前面优化过了
-
如果该帧不是当前关键帧,则
-
获取当前关键帧mpCurrentKF到其共视关键帧pKFi的相对变换
Tic=Tiw*Twc,将Tic分解为Ric和tic -
g2oSic 当前关键帧mpCurrentKF到其共视关键帧pKFi的Sim3相对变化,由Tic分解的Ric和tic得到
g2o::Sim3 g2oSic(Converter::toMatrix3d(Ric),Converter::toVector3d(tic),1.0); -
当前帧的位姿固定不动,其他关键帧根据相对关系得到Sim3调整的位姿
g2o::Sim3 g2oCorrectedSiw = g2oSic*mg2oScw; -
存放闭环g2o优化后当前关键帧的共视关键帧的Sim3 位姿
CorrectedSim3[pKFi]=g2oCorrectedSiw;
-
-
分解共视关键帧世界位姿Tiw得到Riw和tiw
-
将其变为Sim3变化
g2o::Sim3 g2oSiw(Converter::toMatrix3d(Riw),Converter::toVector3d(tiw),1.0); -
存放没有矫正的当前关键帧的共视关键帧的Sim3 变换
NonCorrectedSim3[pKFi]=g2oSiw;
-
-
step 2.2 得到矫正的当前关键帧的共视关键帧位姿后,修正这些共视关键帧的地图点
遍历待矫正的共视关键帧(不包括当前帧),for
-
取出当前帧
-
取出经过位姿传播后的Sim3变换
g2oCorrectedSiw、g2oCorrectedSwi -
取出未经过位姿传播的Sim3变换
g2oSiw -
获取该帧的所有地图点
-
遍历待矫正共视关键帧中的每一个地图点,for
-
如果该地图点无效,则跳过
-
如果该地图点是坏的,则跳过
-
如果该地图点已被矫正了,则跳过
-
矫正过程本质上也是基于当前关键帧的优化后的位姿展开的。
⭐️将该未校正的eigP3Dw先从世界坐标系映射到未校正的pKFi相机坐标系,然后再反映射到校正后的世界坐标系下 ,具体步骤如下 :
-
获取当前地图点的世界位姿
cv::Mat P3Dw = pMPi->GetWorldPos(); -
根据位姿计算的地图点的世界坐标
Eigen::Matrix<double,3,1> eigP3Dw = Converter::toVector3d(P3Dw); -
下面变换是:eigP3Dw: world →g2oSiw→ i →g2oCorrectedSwi→ world 。
// map(P) 内部做了相似变换 s*R*P +t Eigen::Matrix<double,3,1> eigCorrectedP3Dw = g2oCorrectedSwi.map(g2oSiw.map(eigP3Dw)); -
将矫正后的地图点转化为Mat形式,并设置世界位姿
-
记录矫正该地图点的关键帧id,防止重复
-
记录该地图点所在的关键帧id
-
因为地图点更新了,需要更新其平均观测方向以及观测距离范围
-
-
Step 2.3:将共视关键帧的Sim3转换为SE3,根据更新的Sim3,更新关键帧的位姿。其实是现在已经有了更新后的关键帧组中关键帧的位姿,但是在上面的操作时只是暂时存储到了 KeyFrameAndPose 类型的变量中,还没有写回到关键帧对象中。
- 调用toRotationMatrix 可以自动归一化旋转矩阵
- 平移向量中包含有尺度信息,还需要用尺度归一化
- 设置矫正后的新的pose
-
step 2.4 根据共视关系根系当前帧与其他关键帧之间的连接。因为地图点的位置改变了,可能会引起共视关系、权值的改变,所以要更新
pKFi->UpdateConnections();
-
-
step 3 检测当前帧的地图点与经过闭环匹配后该帧的地图点是否存在冲突,对冲突的进行替换或填补
mvpCurrentMatchedPoints 是当前关键帧和闭环关键帧组的所有地图点进行投影得到的匹配点
遍历所有匹配点,for
-
如果当前匹配点存在,则
-
取出同一个索引对应的两种地图点,决定是否要替换
-
获取匹配投影得到的地图点pLoopMP
-
得到当前关键帧原来的地图点pCurMP
-
如果pCurMP存在,说明有重复的地图点,则用匹配的地图点代替现有的。 因为匹配的地图点是经过一系列操作后比较精确的,现有的地图点很可能有累计误差
pCurMP->Replace(pLoopMP); -
如果当前帧没有该地图点,则直接添加。
mpCurrentKF->AddMapPoint(pLoopMP,i); pLoopMP->AddObservation(mpCurrentKF,i); pLoopMP->ComputeDistinctiveDescriptors();
-
-
-
-
-
Step 4:将闭环相连关键帧组mvpLoopMapPoints 投影到当前关键帧组中,进行匹配,融合,新增或替换当前关键帧组中KF的地图点。
因为 闭环相连关键帧组mvpLoopMapPoints 在地图中时间比较久经历了多次优化,认为是准确的。而当前关键帧组中的关键帧的地图点是最近新计算的,可能有累积误差。
CorrectedSim3:存放矫正后当前关键帧的共视关键帧,及其世界坐标系下Sim3 变换
SearchAndFuse(CorrectedSim3); -
Step 5:更新当前关键帧组之间的两级共视相连关系,得到因闭环时地图点融合而新得到的连接关系
-
创建
map<KeyFrame*, set<KeyFrame*> > LoopConnections;LoopConnections:存储因为闭环地图点调整而新生成的连接关系
-
step 5.1 遍历当前帧相连关键帧组(一级相连),并遍历,for
-
获取相连关键帧pKFi
-
step 5.2 获取与相连关键帧pKFi相连的关键帧(二级相连)
-
step 5.3 更新一级相连关键帧的连接关系(会把当前关键帧添加进去,因为地图点已经更新和替换了)
pKFi->UpdateConnections(); -
step 5.4 取出该帧更新后的连接关系
LoopConnections[pKFi]=pKFi->GetConnectedKeyFrames(); -
step 5.5 从连接关系中去除闭环之前的二级连接关系,剩下的连接就是有闭环得到的连接关系(遍历二级相连帧,将其在LoopConnections[pKFi]中删除)
for(vector<KeyFrame*>::iterator vit_prev=vpPreviousNeighbors.begin(), vend_prev=vpPreviousNeighbors.end(); vit_prev!=vend_prev; vit_prev++) { LoopConnections[pKFi].erase(*vit_prev); } -
step 5.6 从连接关系中去除闭环之前的一级连接关系,剩下的连接就是有闭环得到的连接关系(遍历一级相连帧,将其在LoopConnections[pKFi]中删除)
-
-
-
Step 6 进行本质图优化,优化本质图中所有关键帧的位姿和地图点。LoopConnections是形成闭环后新生成的连接关系,不包括步骤7中当前帧与闭环匹配帧之间的连接关系
Optimizer::OptimizeEssentialGraph(mpMap, mpMatchedKF, mpCurrentKF, NonCorrectedSim3, CorrectedSim3, LoopConnections, mbFixScale); -
step 7 添加当前帧与闭环匹配帧之间的边(这个连接关系不优化),它在下一次的本质图优化里面使用
mpMatchedKF->AddLoopEdge(mpCurrentKF); mpCurrentKF->AddLoopEdge(mpMatchedKF); -
step 8 新建一个线程用于全局BA优化。OptimizeEssentialGraph只是优化了一些主要关键帧的位姿,这里进行全局BA可以全局优化所有位姿和MapPoints
-
闭环线程结束,释放局部建图线程
-
将
mLastLoopKFid = mpCurrentKF->mnId;
void LoopClosing::SearchAndFuse(const KeyFrameAndPose &CorrectedPosesMap)
- @brief 将闭环相连关键帧组mvpLoopMapPoints 投影到当前关键帧组中,进行匹配,新增或替换当前关键帧组中KF的地图点
- 因为 闭环相连关键帧组mvpLoopMapPoints 在地图中时间比较久经历了多次优化,认为是准确的
- 而当前关键帧组中的关键帧的地图点是最近新计算的,可能有累积误差
- @param[in] CorrectedPosesMap 矫正的当前KF对应的共视关键帧及Sim3变换
步骤:
-
定义ORB匹配器
-
step 1 遍历待矫正的当前KF的相连关键帧,for
-
获取关键帧信息和矫正过的Sim变换,并将其转换为矩阵形式
-
step 2 将mvpLoopMapPoints投影到pKF帧匹配,检查地图点冲突并融合(mvpLoopMapPoints:与当前关键帧闭环匹配上的关键帧及其共视关键帧组成的地图点)
-
//vpReplacePoints:存储mvpLoopMapPoints投影到pKF匹配后需要替换掉的新增地图点,索引和mvpLoopMapPoints一致,初始化为空 //搜索区域系数为4 matcher.Fuse(pKF,cvScw,mvpLoopMapPoints,4,vpReplacePoints); -
之所以不在上面 Fuse 函数中进行地图点融合更新的原因是需要对地图加锁.
-
step 3 遍历闭环帧组的所有的地图点mvpLoopMapPoints,替换掉需要替换的地图点,for
-
获取当前地图点
-
如果记录了需要替换的地图点,则用mvpLoopMapPoints替换掉vpReplacePoints里记录的要替换的地图点
pRep->Replace(mvpLoopMapPoints[i]);
-
-
-
void LoopClosing::RunGlobalBundleAdjustment(unsigned long nLoopKF)
-
@brief 全局BA线程,这个是这个线程的主函数
-
@param[in] nLoopKF 看上去是闭环关键帧id,但是在调用的时候给的其实是当前关键帧的id
-
// mbStopGBA直接传引用过去了,这样当有外部请求的时候这个优化函数能够及时响应并且结束掉 // 提问:进行完这个过程后我们能够获得哪些信息? // 回答:能够得到全部关键帧优化后的位姿,以及优化后的地图点 -

步骤:
-
记录GBA已经迭代次数,用来检查全局BA过程是否是因为意外结束的。
int idx = mnFullBAIdx; -
step 1 执行全局BA,优化所有的关键帧位姿和地图中地图点
Optimizer::GlobalBundleAdjustemnt(mpMap, // 地图点对象 10, // 迭代次数 &mbStopGBA, // 外界控制 GBA 停止的标志 nLoopKF, // 形成了闭环的当前关键帧的id false); // 不使用鲁棒核函数 -
更新所有的地图点和关键帧,在global BA过程中local mapping线程仍然在工作,这意味着在global BA时可能有新的关键帧产生,但是并未包括在GBA里,所以和更新后的地图并不连续。需要通过spanning tree来传播
-
如果全局BA过程是因为意外结束的,那么直接退出GBA
if (idx!=mnFullBAIdx ) return ; -
如果当前GBA没有中断请求,则更新位姿和地图点,如下
// 如果当前GBA没有中断请求,更新位姿和地图点 // 这里和上面那句话的功能还有些不同,因为如果一次全局优化被中断,往往意味又要重新开启一个新的全局BA;为了中断当前正在执行的优化过程mbStopGBA将会被置位,同时会有一定的时间 // 使得该线程进行响应;而在开启一个新的全局优化进程之前 mbStopGBA 将会被置为False // 因此,如果被强行中断的线程退出时已经有新的线程启动了,mbStopGBA=false,为了避免进行后面的程序,所以有了上面的程序; // 而如果被强行中断的线程退出时新的线程还没有启动,那么上面的条件就不起作用了(虽然概率很小,前面的程序中mbStopGBA置位后很快mnFullBAIdx就++了,保险起见),所以这里要再判断一次-
请求停止局部建图线程
mpLocalMapper->RequestStop(); -
等待知道local mapping 结束才会继续后续操作
while(!mpLocalMapper->isStopped() && !mpLocalMapper->isFinished()) { //usleep(1000); std::this_thread::sleep_for(std::chrono::milliseconds(1)); } -
后续要更新地图所以要上锁
unique_lock<mutex> lock(mpMap->mMutexMapUpdate); -
从第一个关键帧开始矫正关键帧。刚开始只保存了初始化第一个关键帧
list<KeyFrame*> lpKFtoCheck(mpMap->mvpKeyFrameOrigins.begin(),mpMap->mvpKeyFrameOrigins.end()); -
step 2 遍历并更新全局地图中的所有spanning tree中的关键帧,
while(!lpKFtocheck.empty())(有点像是多叉树那样,进行广度优先搜索)// 问:GBA里锁住第一个关键帧位姿没有优化,其对应的pKF->mTcwGBA是不变的吧?那后面调整位姿的意义何在? // 回答:注意在前面essential graph BA里只锁住了回环帧,没有锁定第1个初始化关键帧位姿。所以第1个初始化关键帧位姿已经更新了 // 在GBA里锁住第一个关键帧位姿没有优化,其对应的pKF->mTcwGBA应该是essential BA结果,在这里统一更新了-
获取set集合中最前面的关键帧pKF
-
获取pKF的所有孩子结点
-
获取pKF的位姿转换Twc
-
遍历当前关键帧的所有子关键帧,for
-
获取子关键帧pChild
-
如果该子关键帧pChild没有被标记,则
-
计算从父关键帧到当前子关键帧的位姿变换
Tchildc = pchild->GetPose()*Twc -
利用父关键帧优化后的位姿对子关键帧位姿进行优化
// 再利用优化后的父关键帧的位姿,转换到世界坐标系下,相当于更新了子关键帧的位姿 // 这种最小生成树中除了根节点,其他的节点都会作为其他关键帧的子节点,这样做可以使得最终所有的关键帧都得到了优化 pChild->mTcwGBA = Tchildc*pKF->mTcwGBA; -
标记该该子关键帧
pChild->mnBAGlobalForKF=nLoopKF;
-
-
将该子关键帧存入lpKFtoCheck中
lpKFtoCheck.push_back(pChild);
-
-
记录为矫正的关键帧的位姿
pKF->mTcwBefGBA = pKF->GetPose(); -
记录已经矫正的关键帧的位姿
pKF->SetPose(pKF->mTcwGBA); -
将该关键帧pKF从列表中移除
lpKFtoCheck.pop_front();
-
-
获取所有的地图点
const vector<MapPoint*> vpMPs = mpMap->GetAllMapPoints(); -
step 3 遍历每一个地图点并用更新的关键帧位姿来更新地图点位置,for
-
获取一个地图点
-
如果该地图点是坏点,则跳过,continue
-
如果这个地图点直接参与到了BA优化过程,那么就直接重新设置位姿即可
pMP->SetWorldPos(pMP->mPosGBA); -
如果这个地图点并没有参与到全局BA优化的过程中,那么就使用其参考关键帧的新位姿来优化自己的坐标
-
获取地图点的参考关键帧pRefKF
-
如果该参考关键帧没有经过此次全局BA优化,则跳过,continue
-
获得该参考关键帧全局BA优化前的位姿,并得到旋转和平移Rcw、tcw
cv::Mat Rcw = pRefKF->mTcwBefGBA.rowRange(0,3).colRange(0,3); cv::Mat tcw = pRefKF->mTcwBefGBA.rowRange(0,3).col(3); -
经该地图点转换到参考关键帧的相机坐标系下
cv::Mat Xc = Rcw*pMP->GetWorldPos()+tcw; -
然后使用已经纠正过的参考关键帧的位姿,再将该地图点变换到世界坐标系上,更新地图点位置
cv::Mat Twc = pRefKF->GetPoseInverse(); cv::Mat Rwc = Twc.rowRange(0,3).colRange(0,3); cv::Mat twc = Twc.rowRange(0,3).col(3); pMP->SetWorldPos(Rwc*Xc+twc);
-
-
-
释放局部建图线程,地图更新结束
mpLocalMapper->Release();
-
-
设置参数
mbFinishedGBA = true; mbRunningGBA = false;
-
void LoopClosing::Run( )
- 回环线程主函数
步骤:
-
线程主函数,
while(1)-
Loopclosing中的关键帧是LocalMapping发送过来的,LocalMapping是Tracking中发过来的,在LocalMapping中通过InsertKeyFrame将关键帧插入闭环检测队列mlpLoopKeyFrameQueueStep 1 查看闭环检测队列mlpLoopKeyFrameQueue中有没有关键帧进来
CheckNewKeyFrames(),如果有,则- 如果检测到闭环
DetectLoop(),则- 如果有一个帧通过了Sim3求解与优化
ComputeSim3,则- 进行闭环矫正
CorrectLoop()
- 进行闭环矫正
- 如果有一个帧通过了Sim3求解与优化
- 如果检测到闭环
-
查看是否有外部线程请求复位当前线程
ResetIfRequested() -
查看外部线程是否有终止当前线程的请求,如果有的话就跳出这个线程的主函数的主循环
if(CheckFinish()) break;
-
-
运行到这里说明有外部线程请求终止当前线程,在这个函数中执行终止当前线程的一些操作
SetFinish();
Map.h
参数:
函数:
MapDrawer.h
参数:
函数:
MapPoint.h
参数:
函数:
UpdateNormalAndDepth()
更新地图点的平均观测方向、观测距离范围。
步骤:
- 获取观测到该地图点的所有关键帧、坐标等信息
- 计算该地图点的平均观测方向。将能观测到该地图点的所有关键帧,对该点的观测方向归一化为单位向量,然后进行求和得到该地图点的朝向
- 将所有朝向累加取平均。
- (在这里还计算了该地图点在参考帧中金字塔的层数,然后跟新所能观测到该地图点的距离的上下限,该步是为了在之后的代码中,预测地图点对应的特征点所在的金字塔尺度,根据最大距离/特征点的距离得到)
PredictScale(const float ¤tDist, KeyFrame* pKF)
预测地图单对应特征点所在的图像金字塔尺度层数
直接根据如下公式求解
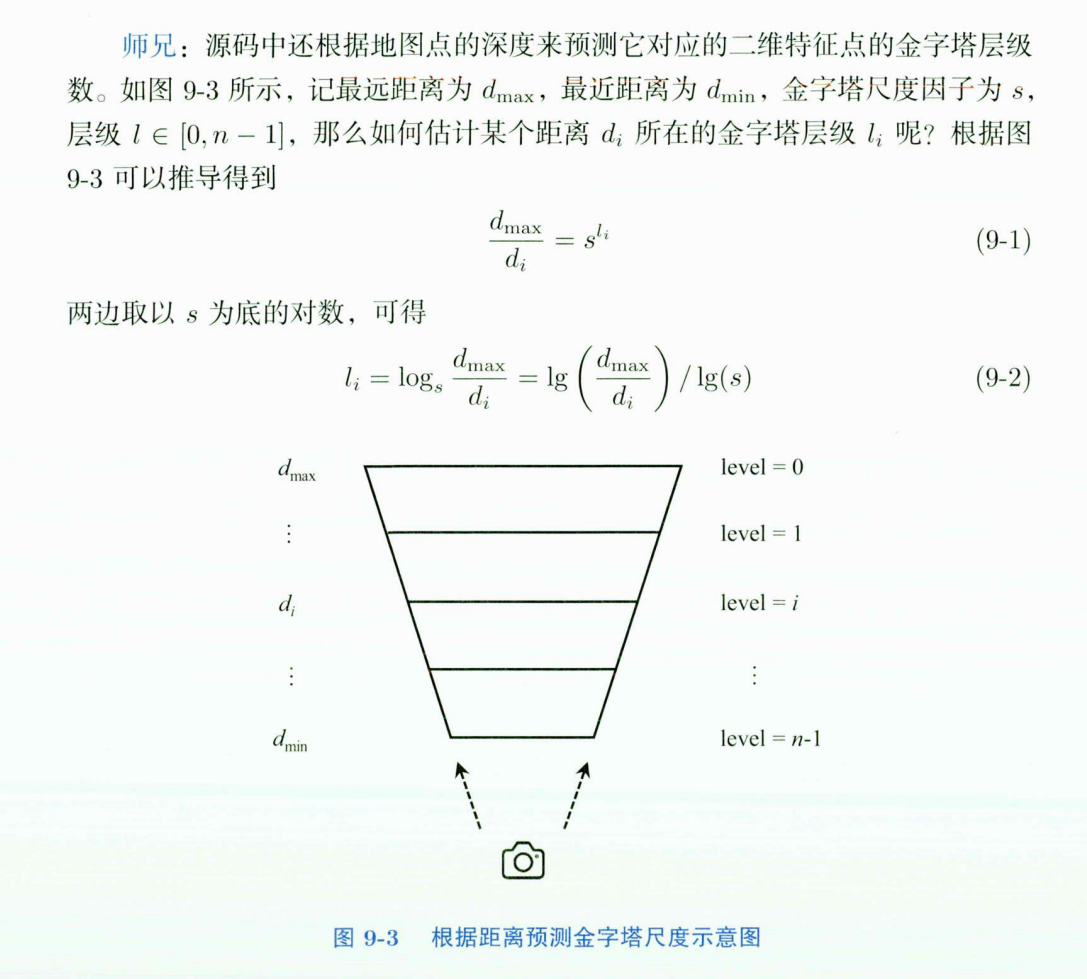
ComputeDistinctiveDescriptors()
计算地图点最具代表性的描述子。
由于一个地图点会被许多相机观测到,因此在插入关键帧后,需要判断是否更新代表当前点的描述子 。先获得当前点的所有描述子,然后计算描述子之间的两两距离,最好的描述子与其他描述子应该具有最小的距离中值
步骤:
- 获取该地图点所有有效的观测关键帧的信息
- 遍历该地图点的所有关键帧,获取并保存所有对应的orb描述子信息
- 使用N x N 的矩阵存储这些描述子两两之间的距离
- 对每一行数据进行排序,计算每一行数据的中值,找到最小中值对应的描述子,即为最具代表性的描述子
- 存储最具代表性的描述子 (该函数就是为了求这个值,其为成员变量)
Optimizer.h
参数:
原理:
g2o框架图



PoseOptimization中的一些问题
ORBSLAM2中的优化(二)-- 在跟踪线程中,使用g2o进行优化,orbslam2代码详细讲解,图优化算法代码讲解 - 知乎 (zhihu.com)
在PoseOptimization的最后,优化结束后只更新了位姿,因为经过跟踪得到的位姿是个粗略值,我们的现在的位姿设置的很不严谨,因此这个位姿的误差是比较大的,我们要首先对他进行单独的优化。
问:优化的对象是什么?
优化的对象是当前帧的位姿
问:优化对象的初始值是什么?根据什么来设定?
初始值是根据恒速运动模型设置的,是在上一帧的位姿 * 上一帧的速度(速度其实就是上一次的位姿变换)
问:观测值是什么?
观测值是帧的特征点坐标
问:真值(或者说先验)是什么?
是 3D世界 地图点,也就是 MapPoint。
问:我们是怎么建立真值和当前观测值的对应关系?或者说地图点和当前帧的关系?
通过对上一帧和当前帧的重投影匹配:
- 将上一帧的特征点投影到当前帧
- 进行匹配
- 匹配成功的,把上一帧的特征点对应的地图点,也对应到当前帧对应的特征点上。也就是把指针赋值给当前帧对应的成员变量。
然后再通过相机模型,就可以建立当前帧对 地图点 的真实观测值了
总结
在这一优化过程中,我们实际上把上一帧之前建立的那些地图点作为了先验的信息,
通过相机模型把这些地图点转化到当前帧的平面上,作为 真值
而我们的特征点坐标就是 观测值
优化的目标就是让这两者的误差变得最小,当误差最小时,得到的位姿就是最优的。
localBA
ORBSLAM2中的优化(三)上–localBA优化、图优化代码详解,边缘化关键帧和路标点的详解,LocalBundleAdjustment详解 - 知乎 (zhihu.com)
ORBSLAM2中的优化(三)下-详解localBA - 知乎 (zhihu.com)



OptimizeSim3
优化的对象时Sim3变换的位姿
初值是有Sim3计算得到的两帧之间的变换,其为第一类顶点
第二类顶点是地图点变换到各自相机坐标系下的坐标,
边为二元边,分为正向投影和反向投影,一个顶点都为待优化的Sim3,另一个顶点为各自的第二类顶点
观测值是地图点对应的各自帧的特征点坐标,真值应该就是地图点
误差 = 观测 -投影
通过优化,使误差越来越小,最后只更新Sim3位姿,不更新地图点,返回内点个数

OptimizeEssentialGraph
闭环矫正中的本质图优化函数OptimizeEssentialGraph用于闭环矫正后优化所有关键帧的位姿。注意,这里不优化地图点。(闭环匹配上的关键帧不进行位姿优化(认为是准确的,作为基准),初始关键帧没有被锁住,也做了优化)
顶点:
待优化的所有关键帧位姿。顶点中关键帧的类型为g2o::VertexSim3Expmap,其中多了一项根据传感器的类型决定是否优化尺度。
边:
数据类型都是二元边g2o::EdgeSim3。
- 第一种:闭环时因为地图点调整而出现的关键帧间的新连接关系。这个对应的是在闭环矫正时的当前帧的一级共视关键帧与二级共视关键帧在矫正后的连接关系LoopConnections。
- 添加跟踪时形成的边、闭环匹配成功形成的边
- 第二种:生成树的边(有父关键帧),因为父关键帧就是和当前帧共视程度最高的关键帧,所有要将父关键帧与当前帧相连
- 第三种:当前帧与闭环匹配帧之间的连接关系(这里面也包括了当前遍历到的这个关键帧之前曾经存在过的回环边)
- 第四种:共视程度超过100的关键帧也作为边进行优化

GlobalBundleAdjustemnt
全局优化函数GlobalBundleAdjustment主要用于优化所有的关键帧位姿和地图点。
这个全局BA优化在本程序中有两个地方使用:
- 1、单目初始化:CreateInitialMapMonocular函数
- 2、闭环优化:RunGlobalBundleAdjustment函数
顶点:
待优化的所有关键帧的位姿和所有地图点。以第0个关键帧位姿作为参考基准,不优化。顶点中关键帧位姿的类型为g2o::VertexSE3Expmap,顶点中地图点的类型为g2o::VertexSBAPointXYZ。
边:
地图点与观测到它的关键帧的投影关系,为二元边。对于单目相机模式,边的类型为g2o::EdgeSE3ProjectXYZ;对于双目相机和RGB-D相机模式,边的类型为g2o::EdgeStereoSE3ProjectXYZ。
顶点与边的定义与局部建图线程中的局部地图优化函数LocalBundleAdjustment一样。

函数:
int Optimizer::PoseOptimization(Frame *pFrame)
- 该优化函数主要用于Tracking线程中:运动跟踪、参考帧跟踪、地图跟踪、重定位
- @brief Pose Only Optimization
- 3D-2D 最小化重投影误差 e = (u,v) - project(Tcw*Pw) \n
- 只优化Frame的Tcw,不优化MapPoints的坐标
-
- Vertex: g2o::VertexSE3Expmap(),即当前帧的Tcw
-
- Edge:
-
- g2o::EdgeSE3ProjectXYZOnlyPose(),BaseUnaryEdge
-
- Vertex:待优化当前帧的Tcw
-
- measurement:MapPoint在当前帧中的二维位置(u,v)
-
- InfoMatrix: invSigma2(与特征点所在的尺度有关)
-
- g2o::EdgeStereoSE3ProjectXYZOnlyPose(),BaseUnaryEdge
-
- Vertex:待优化当前帧的Tcw
-
- measurement:MapPoint在当前帧中的二维位置(ul,v,ur)
-
- InfoMatrix: invSigma2(与特征点所在的尺度有关)
- @param pFrame Frame
- @return inliers数量
- ORBSLAM2中的优化(二)-- 在跟踪线程中,使用g2o进行优化,orbslam2代码详细讲解,图优化算法代码讲解 - 知乎 (zhihu.com)
步骤:
-
step 1:构造g2o优化器,BlockSolver_6_3表示:位姿_PoseDim 为6维,路标点 _LandmarkDim 是3维
-
第一步:创建一个线性求解器LinearSolver
g2o::BlockSolver_6_3::LinearSolverType * linearSolver; -
第二步:创建BlockSolver,并用上面定义的线性求解器初始化
linearSolver = new g2o::LinearSolverDense<g2o::BlockSolver_6_3::PoseMatrixType>(); g2o::BlockSolver_6_3 * solver_ptr = new g2o::BlockSolver_6_3(linearSolver); -
第三步:创建总求解器solver,并从GN,LM,DogLeg中选一个,再用上述块求解器BlockSolver初始化
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr); -
第四步:创建终极大boss,稀疏优化器(SparseOptimizer)
g2o::SparseOptimizer optimizer; optimizer.setAlgorithm(solver); -
设置一个统计量,统计输入的帧中,有效的,参与优化过程的2D-3D点对
int nInitialCorrespondences=0;
-
-
step 2:添加顶点:待优化当前帧的Tcw
g2o::VertexSE3Expmap * vSE3 = new g2o::VertexSE3Expmap(); vSE3->setEstimate(Converter::toSE3Quat(pFrame->mTcw)); // 设置id vSE3->setId(0); // 要优化的变量,所以不能固定 vSE3->setFixed(false); optimizer.addVertex(vSE3); // Set MapPoint vertices const int N = pFrame->N; // for Monocular vector<g2o::EdgeSE3ProjectXYZOnlyPose*> vpEdgesMono; vector<size_t> vnIndexEdgeMono; vpEdgesMono.reserve(N); vnIndexEdgeMono.reserve(N); // for Stereo vector<g2o::EdgeStereoSE3ProjectXYZOnlyPose*> vpEdgesStereo; vector<size_t> vnIndexEdgeStereo; vpEdgesStereo.reserve(N); vnIndexEdgeStereo.reserve(N); // 自由度为2的卡方分布,显著性水平为0.05,对应的临界阈值5.991 const float deltaMono = sqrt(5.991); // 自由度为3的卡方分布,显著性水平为0.05,对应的临界阈值7.815 const float deltaStereo = sqrt(7.815); -
step 3:添加一元边
-
锁定地图点。由于需要使用地图点来构造顶点和边,因此不希望在构造的过程中部分地图点被改写造成不一致甚至是段错误
unique_lock<mutex> lock(MapPoint::mGlobalMutex); -
遍历当前地图中的所有地图点,for
-
获取地图点
-
如果该地图点还存在,没有被剔除掉,则继续下面的操作。
-
如果是单目情况,则
-
有效点对数加1
nInitialCorrespondences++ -
将该地图点暂时初始化设置为内点
pFrame->mvbOutlier[i]=false ; -
获取这个地图点的观测并存储
Eigen::Matrix <double,2,1>obs; const cv::KeyPoint &kpUn =pFrame->mvKeysUn[i]; obs<<kpUn.pt.x,kpUn.pt.y; -
新建单目的边,一元边,误差为观测特征点坐标减去投影点的坐标
g2o::EdgeSE3ProjectXYZOnlyPose* e = new g2o::EdgeSE3ProjectXYZOnlyPose(); -
设置边的顶点
e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(0))); e->setMeasurement(obs); -
这个点的可信程度和特征点所在的图层有关
const float invSigma2 = pFrame->mvInvLevelSigma2[kpUn.octave]; e->setInformation(Eigen::Matrix2d::Identity()*invSigma2); -
创建鲁棒核函数
g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber; e->setRobustKernel(rk); rk->setDelta(deltaMono); // 前面提到过的卡方阈值 -
设置相机内参
e->fx = pFrame->fx; e->fy = pFrame->fy; e->cx = pFrame->cx; e->cy = pFrame->cy; -
获取地图点的空间位置,作为迭代的初始值
cv::Mat Xw = pMP->GetWorldPos(); e->Xw[0] = Xw.at<float>(0); e->Xw[1] = Xw.at<float>(1); e->Xw[2] = Xw.at<float>(2); -
存储一元边e
optimizer.addEdge(e); vpEdgesMono.push_back(e); vnIndexEdgeMono.push_back(i);
-
-
如果是双目情况,则
-
有效点对数加1
nInitialCorrespondences++ -
将该地图点暂时初始化设置为内点
pFrame->mvbOutlier[i]=false ; -
获取观测点,(双目相较于单目多了一项右目坐标)
Eigen::Matrix<double,3,1> obs;// 这里和单目不同 const cv::KeyPoint &kpUn = pFrame->mvKeysUn[i]; const float &kp_ur = pFrame->mvuRight[i]; obs << kpUn.pt.x, kpUn.pt.y, kp_ur;// 这里和单目不同 -
新建边,一元边,误差为观测特征点坐标减去投影点的坐标
g2o::EdgeStereoSE3ProjectXYZOnlyPose* e = new g2o::EdgeStereoSE3ProjectXYZOnlyPose();// 这里和单目不同 e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(0))); e->setMeasurement(obs); -
置信程度主要是看左目特征点所在的图层,以下基本和单目一样
//置信程度主要是看左目特征点所在的图层 const float invSigma2 = pFrame->mvInvLevelSigma2[kpUn.octave]; Eigen::Matrix3d Info = Eigen::Matrix3d::Identity()*invSigma2; e->setInformation(Info); //创建鲁棒核函数 g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber; e->setRobustKernel(rk); rk->setDelta(deltaStereo); //获取相机内参 e->fx = pFrame->fx; e->fy = pFrame->fy; e->cx = pFrame->cx; e->cy = pFrame->cy; e->bf = pFrame->mbf; cv::Mat Xw = pMP->GetWorldPos(); e->Xw[0] = Xw.at<float>(0); e->Xw[1] = Xw.at<float>(1); e->Xw[2] = Xw.at<float>(2); //存储一元边 optimizer.addEdge(e); vpEdgesStereo.push_back(e); vnIndexEdgeStereo.push_back(i);
-
-
-
-
如果没有足够的匹配点,那么就只好放弃了
if(nInitialCorrespondences<3) return 0; -
step 4:开始优化,总共优化四次,每次迭代10次,每次优化后,将观测分为outlier和inlier,outlier不参与下次优化。由于每次优化后是对所有的观测进行outlier和inlier判别,因此之前被判别为outlier有可能变成inlier,反之亦然
-
设置阈值(基于卡方检验计算出的阈值(假设测量有一个像素的偏差))
const float chi2Mono[4]={5.991,5.991,5.991,5.991}; // 单目 const float chi2Stereo[4]={7.815,7.815,7.815, 7.815}; // 双目 const int its[4]={10,10,10,10};// 四次迭代,每次迭代的次数 -
设置遍历,统计bad的地图点个数
int nBad=0; -
一共进行四次优化,for
-
设置待优化的关键帧位姿
vSE3->setEstimate(Converter::toSE3Quat(pFrame->mTcw)); -
初始化优化器,这里的参数0就算是不填写,默认也是0,也就是支队level为0的边进行优化
optimizer.initializeOptimization(0); -
开始优化,优化10次
optimizer.optimize(its[it]); -
令
nBad=0 -
优化结束,开始遍历参与优化的每一条误差边(单目),for
-
获取该边的信息
g2o::EdgeSE3ProjectXYZOnlyPose* e = vpEdgesMono[i]; -
获取该边的索引
const size_t idx = vnIndexEdgeMono[i]; -
如果这条误差边是来自于outlier,则计算误差
if(pFrame->mvbOutlier[idx]) e->computeError(); -
error*\Omega*error,表征了这个点的误差大小(考虑置信度以后)
const float chi2 = e->chi2(); -
根据chi2和阈值,判断该点是否为内点。如果
chi2>chi2Mono[it],则该点为外点,pFrame->mvbOutlier[idx]=true; e->setLevel(1); // 设置为outlier , level 1 对应为外点,上面的过程中我们设置其为不优化 nBad++; -
否则,该点为内点
pFrame->mvbOutlier[idx]=false; e->setLevel(0); // 设置为inlier, level 0 对应为内点,上面的过程中我们就是要优化这些关系 -
除了前两次优化需要RobustKernel以外, 其余的优化都不需要 – 因为重投影的误差已经有明显的下降了
if(it==2) e->setRobustKernel(0);
-
-
同样的原理遍历双目的误差边(双目),for
- 获取误差边
- 获取该边的索引
- 如果该边对应的点为外点,则计算误差
- 计算卡方检验的置信度chi2
- 如果chi2大于阈值,则设置该点为外点
- 否则,则设置该点为内点
- 除了前两次优化需要RobustKernel以外,其余的优化都不需要–因为重投影的误差已经有明显的下降了
-
如果优化中边数小于10 ,则退出循环,break
-
-
-
step 5:得到优化后的当前帧的位姿
g2o::VertexSE3Expmap* vSE3_recov = static_cast<g2o::VertexSE3Expmap*>(optimizer.vertex(0)); g2o::SE3Quat SE3quat_recov = vSE3_recov->estimate(); cv::Mat pose = Converter::toCvMat(SE3quat_recov); pFrame->SetPose(pose); -
返回内点数目
nInitialCorrespondences - nBad
void Optimizer::LocalBundleAdjustment(KeyFrame pKF, bool pbStopFlag, Map* pMap)
- @brief Local Bundle Adjustment
- 该优化函数用于LocalMapping线程的局部BA优化
-
- Vertex:
-
- g2o::VertexSE3Expmap(),LocalKeyFrames,即当前关键帧的位姿、与当前关键帧相连的关键帧的位姿
-
- g2o::VertexSE3Expmap(),FixedCameras,即能观测到LocalMapPoints的关键帧(并且不属于LocalKeyFrames)的位姿,在优化中这些关键帧的位姿不变
-
- g2o::VertexSBAPointXYZ(),LocalMapPoints,即LocalKeyFrames能观测到的所有MapPoints的位置
-
- Edge:
-
- g2o::EdgeSE3ProjectXYZ(),BaseBinaryEdge
-
- Vertex:关键帧的Tcw,MapPoint的Pw
-
- measurement:MapPoint在关键帧中的二维位置(u,v)
-
- InfoMatrix: invSigma2(与特征点所在的尺度有关)
-
- g2o::EdgeStereoSE3ProjectXYZ(),BaseBinaryEdge
-
- Vertex:关键帧的Tcw,MapPoint的Pw
-
- measurement:MapPoint在关键帧中的二维位置(ul,v,ur)
-
- InfoMatrix: invSigma2(与特征点所在的尺度有关)
- @param pKF KeyFrame
- @param pbStopFlag 是否停止优化的标志
- @param pMap 在优化后,更新状态时需要用到Map的互斥量mMutexMapUpdate
- @note 由局部建图线程调用,对局部地图进行优化的函数
步骤:
-
创建存储局部关键帧的列表
list<KeyFrame*>lLocalKeyFrames; -
step 1 将当前帧及其共视关键帧加入局部关键帧中
- 将当前帧加入局部关键帧中,并标记该帧
- 找到关键帧连接的共视关键帧(一级相连),加入局部关键帧中,for
- 获取一个共视关键帧
- 把参与局部BA的每一个关键帧的mnBALocalForKF设置为当前关键帧的mnId,防止重复添加
- 如果该帧有效,则加入局部关键帧中
-
step 2 遍历局部关键帧中(一级相连)关键帧,将它们观测的地图点加入到局部地图点
- 创建存储局部地图点的列表
list<MapPoint*>lLocalMapPoints; - 遍历局部关键帧中的每一个关键帧,for
- 取出该关键帧对应的地图点
- 遍历这个关键帧观测到的每一个地图点,加入到局部地图点中,for
- 获取一个地图点
- 如果该点存在,则继续下一步
- 如果该点不是坏点,则继续下一步
- 如果该点没有被标记过,则将该点加入局部地图点列表中,并将其标记
- 创建存储局部地图点的列表
-
step 3 得到能被局部地图点观测到,但不属于局部关键帧的关键帧(二级相连),这些二级相连关键帧在局部BA优化时不优化
-
创建存储固定关键帧的列表
list<KeyFrame*>lFixedCameras; -
遍历局部地图中的每个地图点,for
-
获取观测到该地图点的KF和该地图点在KF中的索引
map<KeyFrame*,size_t> observations = (*lit)->GetObservations(); -
遍历所有观测到该地图点的关键帧,for
- 如果该帧不属于局部关键帧且没被固定关键帧标记,则标记该关键帧,如果该帧不是坏的,则加入
lFixedCameras中
- 如果该帧不属于局部关键帧且没被固定关键帧标记,则标记该关键帧,如果该帧不是坏的,则加入
-
-
-
step 4 构造g2o优化器
-
创建一个线性求解器linearSlover
g2o::BlocakSolver_6_3::LinearSolverType * linearSolver; -
创建BlockSolver,并用上面定义的线性求解器初始化
linearSolver=new g2o::LinearSolverEigen<g2o::BlockSolver_6_3::PoseMatrixType>(); g2o::BlockSolver_6_3 * solver_ptr = new g2o::BlockSolver_6_3(linearSolver); -
创建总求解器solver,并从GN,LM,DogLeg中选一个,再用上述块求解器BlockSolver初始化
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr); -
创建稀疏优化器(SparseOptimizer)
g2o::SparseOptimizer optimizer; optimizer.setAlgorithm(solver); -
设置外界的停止优化标志,可能在 Tracking::NeedNewKeyFrame() 里置位
if(pbStopFlag) optimizer.setForceStopFlag(pbStopFlag); -
记录参与局部BA的最大关键帧mnId
unsigned long maxKFid = 0;
-
-
step 5 添加待优化的位姿顶点:局部关键帧的位姿,for
-
获取关键帧
-
创建顶点类型
g2o::VertexSE3Expmap *vSE3 = new g2o::VertexSE3Expmap(); -
设置初始优化位姿
vSE3->setEstimae(Converter::toSE3Quat(pKFi->GetPose())); vSE3->setId(pKFi->mnId); -
如果是初始关键帧,要锁住位姿不优化
vSE3->setFixed(pKFi->mnId==0); -
向优化器中加入该顶点
optimizer.addVertex(vSE3); -
记录参与局部BA的最大关键帧mnId
-
-
step 6 添加不优化的位姿顶点:固定关键帧的位姿,注意这里调用了
vSE3->setFixed(true)不优化为啥也要添加?回答:为了增加约束信息
-
遍历所有固定关键帧lFixedCameras,for
-
获取该关键帧
-
创建顶点类型
g2o::VertexSE3Expmap *vSE3 = new g2o::VertexSE3Expmap(); -
设置初始优化位姿
vSE3->setEstimate(Converter::toSE3Quat(pKFi->GetPose())); vSE3->setId(pKFi->mnId); -
所有的这些顶点的位姿都不优化,只是为了增加约束项
vSE3->setFixed(true); -
向优化器中添加顶点
optimizer.addVertex(vSE3); -
记录参与局部BA的最大关键帧mnId
-
-
-
step 7 添加待优化的局部地图点顶点
边的最大数目 = 位姿数目 * 地图点数目
const int nExpectedSize = (lLocalKeyFrames.size()+lFixedCameras.size())*lLocalMapPoints.size(); -
初始化变量
vector<g2o::EdgeSE3ProjectXYZ*> vpEdgesMono; vpEdgesMono.reserve(nExpectedSize); vector<KeyFrame*> vpEdgeKFMono; vpEdgeKFMono.reserve(nExpectedSize); vector<MapPoint*> vpMapPointEdgeMono; vpMapPointEdgeMono.reserve(nExpectedSize); vector<g2o::EdgeStereoSE3ProjectXYZ*> vpEdgesStereo; vpEdgesStereo.reserve(nExpectedSize); vector<KeyFrame*> vpEdgeKFStereo; vpEdgeKFStereo.reserve(nExpectedSize); vector<MapPoint*> vpMapPointEdgeStereo; vpMapPointEdgeStereo.reserve(nExpectedSize); // 自由度为2的卡方分布,显著性水平为0.05,对应的临界阈值5.991 const float thHuberMono = sqrt(5.991); // 自由度为3的卡方分布,显著性水平为0.05,对应的临界阈值7.815 const float thHuberStereo = sqrt(7.815); -
遍历所有的局部地图点,for
-
获取地图点
-
添加顶点:MapPoint (这里就是添加了第三种顶点,也就是地图点。同时把这些路标点设置为了边缘化,不过需要注意的是:是为了在计算求解过程中,先消去路标点,求解相机位姿,再使用相机位姿去求解地图点。目的是加速求解,而不是真的把路标点边缘化。)
MapPoint* pMP=*lit; g2o::VertexSBAPointXYZ* vPoint = bew g2o::VertexSBAPointXYZ(); vPoint->setEstimate(Converter::toVector3d(pMP->GetWorldPos())); //前面记录maxKFid的作用在这里体现 int id=pMP->mnId+maxKFid+1; vPoint->setId(id); //因为使用了LinearSolverType,所以需要将所有的三维点边缘化掉 vPoint->setMarginalized(true); optimizer.addVertex(vPoint); -
获取观测到该地图点的KF和该地图点在KF中的索引
const map<KeyFrame*,size_t> observations = pMP->GetObservations(); -
step 8 在添加完了一个地图点之后,对每一关联的地图点和关键帧构建边。
遍历所有观测到当前地图点的关键帧,for
-
获取一个关键帧
-
如果该帧不是坏的,则继续下面的操作
-
获取观测点坐标
const cv::KeyPoint &kpUn = pKFi -> mvKeysUn[mit->second]; -
如果右目数据不存在,说明是单目模式,则
-
获取观测点坐标
Eigen::Matrix<double,2,1>obs; obs<<kpUn.pt.x,kpUn.pt.y; -
创建边的变量
g2o::EdgeSE3ProjectXYZ* e = new g2o::EdgeSE3ProjectXYZ(); -
边的第一个顶点是地图点
e->setVertex(0,dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id))); -
边的第二个顶点是观测到该地图点的关键帧
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pKFi->mnId))); -
添加观测点
e->setMeasurement(obs); -
设置权重为特征点所在图像金字塔的层数的倒数
const float &invSigma2 = pKFi->mvInvLevelSigma2[kpUn.octave]; e->setInformation(Eigen::Matrix2d::Identity()*invSigma2); -
使用鲁棒核函数抑制外点
g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber; e->setRobustKernel(rk); rk->setDelta(thHuberMono); -
设置相机内参
e->fx=pKFi->fx; e->fy=pKFi->fy; e->cx=pKFi->cx; e->cy=pKFi->cy; -
将边添加到优化器,记录边、边连接的关键帧、边连接的地图点信息
optimizer.addEdge(e); vpEdgesMono.push_back(e); cpEdgeKFMono.push_back(pKFi); vpMapPointEdgeMono.push_back(pMP);
-
-
如果是右目数据存在,说明是双目或RGBD模式,则其过程与单目模式类似
- 获取观测点坐标(包含一个右目坐标)
- 创建边的变量e
- 边的第一个顶点为地图点
- 边的第二个顶点为关键帧
- 添加观测点信息
- 设置权重为特征点所在图像金字塔的层数的倒数
- 使用鲁棒核函数抑制外点
- 设置相机内参
- 将边添加到优化器,记录边、边连接的关键帧、边连接的地图点信息
-
-
-
开始BA前再次确认是否有外部请求停止优化,因为这个变量是引用传递,会随外部变化。可能在 Tracking::NeedNewKeyFrame(), mpLocalMapper->InsertKeyFrame 里置位
if(pbStopFlag) if(*pbStopFlag) return ; -
step 9 分成两个阶段开始优化
-
第一阶段优化,先初始化参数
optimizer.initializeOptimization(); -
迭代5次
optimizer.optimize(5); -
检测是否外部请求停止
if(pbStopFlag) if(*pbStopFlag) bDoMore = false; -
如果有外部请求停止,那么就不再进行第二阶段的优化;如果没有外部请求停止,则
-
step 10 检测outlier,并设置下次不优化
遍历所有的单目误差边,for
-
获取误差边
-
获取地图点
-
如果该点是坏点,则跳过,contin
-
基于卡方检验计算出的阈值(假设测量有一个像素的偏差)。自由度为2的卡方分布,显著性水平为0.05,对应的临界阈值5.991。如果当前边误差超出阈值,或者边链接的地图点深度值为负,说明这个边有问题,不优化
if (e->chi2()>5.991||!e->isDepthPositive()) e->setLevel(1); -
第二阶段优化的时候就属于精求解了,所以就不使用核函数
e->setRobustKernel(0);
-
-
对于所有的双目误差边也都进行类似的操作,遍历所有双目误差边,for
- 获取创建误差边
- 获取地图点
- 如果地图点是坏的,则跳过,continue
- 进行卡方阈值检验,如果超出阈值,或者边连接的地图点深度值为负,说明这个边有问题,不优化
- 不使用核函数
-
step 11 排除误差较大的outlier后再次优化 – 第二阶段优化
optimizer.initializeOptimization(0); optimizer.optimize(10);
-
-
-
创建存储删除点的变量
vector>pair<KeyFrame*,MapPoint*>>vToErase; vToErase.reserve(vpEdgesMono.size()+vpEdgesStereo.size()); -
step 12 在优化后重新计算误差,剔除连接误差比较大的关键帧和地图点
-
对于单目误差边,遍历所有单目误差边,for
-
获取误差边
-
获取地图点
-
如果地图点是坏的,则跳过,continue
-
基于卡方检验计算出的阈值(假设测量有一个像素的偏差),自由度为2的卡方分布,显著性水平为0.05,对应的临界阈值5.991,如果 当前边误差超出阈值,或者边链接的地图点深度值为负,说明这个边有问题,要删掉了。
if(e->chi2()>5.991||!e->isDepthPositive()) { //outlier KeyFrame * pKFi=vpEdgeKFMono[i]; vToErase.push_back(make_pair(pKFi,pMP);) }
-
-
对于双目误差边,遍历所有双目误差边,for
- 获取误差边
- 获取地图点
- 如果地图点是坏的,则跳过,continue
- 基于卡方检验计算出的阈值(假设测量有一个像素的偏差),自由度为3的卡方分布,显著性水平为0.05,对应的临界阈值7.815,如果 当前边误差超出阈值,或者边链接的地图点深度值为负,说明这个边有问题,要删掉了。
-
-
获取地图互斥量
-
删除点,连接偏差比较大,在关键帧中剔除对该地图点的观测;连接偏差比较大,在地图点中剔除对该关键帧的观测
- 如果vToErase不为空,则
- 遍历vToErase,for
- 获取关键帧
- 获取地图点
- 在关键帧中剔除对该地图点的观测
- 在地图点中剔除对该关键帧的观测
- 遍历vToErase,for
- 如果vToErase不为空,则
-
step 13 优化后更新关键帧位姿以及地图点的位置、平均观测方向等属性
-
遍历所有局部关键帧,for
-
获取关键帧
KeyFrame* pKF = *lit; -
获取经过优化后该关键帧的顶点信息
g2o::VertexSE3Expmap* vSE3 = static_cast<g2o::VertexSE3Expmap*>(optimizer.vertex(pKF->mnId)); -
计算顶点的估计值
g2o::SE3Quat SE3quat = vSE3->estimate(); -
更新关键帧位姿
pKF->SetPose(Converter::toCvMat(SE3quat));
-
-
遍历所有局部地图点,for
-
获取地图点信息
MapPoint* pMP = *lit; -
获取经过优化后该地图点的顶点信息
g2o::VertexSBAPointXYZ* vPoint = static_cast<g2o::VertexSBAPointXYZ*>(optimizer.vertex(pMP->mnId+maxKFid+1)); -
更新地图点位置
pMP->SetWorldPos(Converter::toCvMat(vPoint->estimate())); -
更新该点的平均观测方向
pMP->UpdateNormalAndDepth();
-
-
int Optimizer::OptimizeSim3(KeyFrame *pKF1, KeyFrame *pKF2, vector<MapPoint *> &vpMatches1, g2o::Sim3 &g2oS12, const float th2, const bool bFixScale)
- 仅对形成闭环的Sim(3)位姿进行优化,不优化地图点
- 优化两帧之间的Sim3变换,在闭环线程的
ComputeSim3()中用到 - @brief 形成闭环时固定(不优化)地图点进行Sim3位姿优化
-
- Vertex:
-
- g2o::VertexSim3Expmap(),两个关键帧的位姿
-
- g2o::VertexSBAPointXYZ(),两个关键帧共有的MapPoints
-
- Edge:
-
- g2o::EdgeSim3ProjectXYZ(),BaseBinaryEdge
-
- Vertex:关键帧的Sim3,MapPoint的Pw
-
- measurement:MapPoint在关键帧中的二维位置(u,v)
-
- InfoMatrix: invSigma2(与特征点所在的尺度有关)
-
- g2o::EdgeInverseSim3ProjectXYZ(),BaseBinaryEdge
-
- Vertex:关键帧的Sim3,MapPoint的Pw
-
- measurement:MapPoint在关键帧中的二维位置(u,v)
-
- InfoMatrix: invSigma2(与特征点所在的尺度有关)
- @param[in] pKF1 当前帧
- @param[in] pKF2 闭环候选帧
- @param[in] vpMatches1 两个关键帧之间的匹配关系
- @param[in] g2oS12 两个关键帧间的Sim3变换,方向是从2到1
- @param[in] th2 卡方检验是否为误差边用到的阈值
- @param[in] bFixScale 是否优化尺度,单目进行尺度优化,双目/RGB-D不进行尺度优化
- @return int 优化之后匹配点中内点的个数
步骤:
-
step 1 初始化g2o优化器
-
构造线性求解优化器,Hx=-b的求解器
g2o::BlockSolverX::LinearSolverType *linearSolver; -
使用dense的求解器,(常见非dense求解器有cholmod线性求解器和shur补线性求解器)
linearSolver= new g2o::LinearSolverDense< g2o::BlockSolverX::PoseMatrixType>(); -
创建BlockSolver,并用上面定义的线性求解器初始化
g2o::BlockSolverX *solver_ptr = new g2o::BlockSolverX(linearSolver); -
创建总求解器solver,使用L-M迭代
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr); -
创建稀疏优化器(SparseOptimizer)
g2o::SparseOptimizer optimizer; optimizer.setAlgorithm(solver);
-
-
获取内参矩阵
const cv::Mat &K1=pKF1->mK; const cv::Mat &K2=pKF2->mK; -
获取相机的位姿
-
step 2 设置待优化的Sim3位姿作为顶点
-
构建顶点变量
g2o::VertexSim3Expmap * vSim3 = new g2o::VertexSim3Expmap(); -
根据传感器类型决定是否固定尺度
vSim3->_fix_scale=bFixScale; -
设置初值
vSim3->setEstimate(g2oS12); vSim3->setId(0); -
Sim3 需要优化
vSim3->setFixed(false); // 因为要优化Sim3顶点,所以设置为false vSim3->_principle_point1[0] = K1.at<float>(0,2); // 光心横坐标cx vSim3->_principle_point1[1] = K1.at<float>(1,2); // 光心纵坐标cy vSim3->_focal_length1[0] = K1.at<float>(0,0); // 焦距 fx vSim3->_focal_length1[1] = K1.at<float>(1,1); // 焦距 fy vSim3->_principle_point2[0] = K2.at<float>(0,2); vSim3->_principle_point2[1] = K2.at<float>(1,2); vSim3->_focal_length2[0] = K2.at<float>(0,0); vSim3->_focal_length2[1] = K2.at<float>(1,1); -
添加顶点
optimizer.addVertex(vSim3);
-
-
step 3 设置匹配的地图点作为顶点
-
获取匹配点对的个数
const int N = vpMatches1.size(); -
获取pKF1的所有地图点
const vector<MapPoint*>vpMapPoints1 = pKF1->GetMapPointMatches(); -
构建并初始化变量
vector<g2o::EdgeSim3ProjectXYZ*> vpEdges12; //pKF2对应的地图点到pKF1的投影边 vector<g2o::EdgeInverseSim3ProjectXYZ*> vpEdges21; //pKF1对应的地图点到pKF2的投影边 vector<size_t> vnIndexEdge; //边的索引 vnIndexEdge.reserve(2*N); vpEdges12.reserve(2*N); vpEdges21.reserve(2*N); -
核函数的阈值
const float deltaHuber = sqrt(th2); -
遍历每对匹配点,for
-
如果该处匹配关系不存在,则跳过,continue
-
获取匹配的地图点pMP1和pMP2
MapPoint* pMP1 = vpMapPoints1[i]; MapPoint* pMP2 = vpMapches[1]; -
保证顶点的id能够错开
const int id1 = 2*i+1; const int id2 = 2*(i+1); -
i2是pMP2在pKF2中对应的索引
const int i2 = pMP2->GetIndexInKeyFrame(pKF2); -
如果pMP1和pMP2都存在,则
-
如果pMP1和pMP2都不是坏点,且i2>=0,则
-
如果这对匹配点都靠谱,并且对应的2D特征点也都存在的话,添加PointXYZ顶点
-
开始添加第一个地图点vPoint1
g2o::VertexSBAPointXYZ* vPoint1= new g2o::VertexSBAPointXYZ(); -
将地图点转换到各自相机坐标系下的三维点
-
设置vPoint1的初始估计和Id
-
设置地图点不优化
-
将地图点存入optimizer中
-
对第二个地图点vPoint2也进行ii~vi的操作
-
-
否则,跳过,continue
-
-
否则,跳过,continue
-
对匹配关系进行计数
-
step 4 添加边(地图点投影到特征点)
Set edge x1=S12*X2
-
获取地图点pMP1对应的观测地图点
-
step 4.1 闭环候选帧地图点投影到当前关键帧的边 – 正向投影
-
创建边的变量
g2o::EdgeSim3ProjectXYZ* e12 = new g2o::EdgeSim3ProjectXYZ(); -
设置第一个顶点,vertex(id2)对应的是pKF2 VertexSBAPointXYZ 类型的三维点
e12->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id2))); -
设置第二个顶点。为什么这里添加的节点的id为0?回答:因为vertex(0)对应的是 VertexSim3Expmap 类型的待优化Sim3,其id 为 0
e12->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(0))); e12->setMeasurement(obs1); -
信息矩阵和这个特征点的可靠程度(在图像金字塔中的图层)有关
const float &invSigmaSquare1 = pKF1->mvInvLevelSigma2[kpUn1.octave]; e12->setInformation(Eigen::Matrix2d::Identity()*invSigmaSquare1); -
构建并使用鲁棒核函数
-
设置鲁棒核函数的参数
-
向优化器中加入边e12
-
-
step 4.2 当前关键帧地图点投影到闭环候选帧的边 – 反向投影
Set edge x2 = S21*X1
-
获取地图点pMP2对应的观测特征点
-
创建边的变量e21
g2o::EdgeInverseSim3ProjectXYZ* e21 = new g2o::EdgeInverseSim3ProjectXYZ(); -
后面步骤与4.1相同
// vertex(id1)对应的是pKF1 VertexSBAPointXYZ 类型的三维点,内部误差公式也不同 e21->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id1))); e21->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(0))); e21->setMeasurement(obs2); float invSigmaSquare2 = pKF2->mvInvLevelSigma2[kpUn2.octave]; e21->setInformation(Eigen::Matrix2d::Identity()*invSigmaSquare2); g2o::RobustKernelHuber* rk2 = new g2o::RobustKernelHuber; e21->setRobustKernel(rk2); rk2->setDelta(deltaHuber); optimizer.addEdge(e21); vpEdges12.push_back(e12); vpEdges21.push_back(e21); vnIndexEdge.push_back(i);
-
-
-
-
-
step 5 g2o开始优化,先迭代5次
optimizer.initializeOptimization(); optimizer.optimize(5); -
step 6 用卡方检验剔除误差大的边,(检验内点)
-
遍历所有的pKF2的地图点到pKF1的投影边vpEdges12,for
-
获取一条边e12
-
获取其反向投影边e21
-
如果e12或者e21不存在,则跳过,continue
-
进行卡方检验,如果正向投影或反向投影任意一个超过误差阈值,就删掉该边
if(e12->chi2()>th2 || e21->chi2()>th2) { // 正向或反向投影任意一个超过误差阈值就删掉该边 size_t idx = vnIndexEdge[i]; vpMatches1[idx]=static_cast<MapPoint*>(NULL); optimizer.removeEdge(e12); optimizer.removeEdge(e21); vpEdges12[i]=static_cast<g2o::EdgeSim3ProjectXYZ*>(NULL); vpEdges21[i]=static_cast<g2o::EdgeInverseSim3ProjectXYZ*>(NULL); // 累计删掉的边 数目 nBad++; }
-
-
如果有误差较大的边被剔除,说明回环质量并不是非常好,还要多迭代几次;反之就少迭代几次
int nMoreIterations; if(nBad>0) nMoreIterations=10; else nMoreIterations=5; -
如果经过上面的剔除后剩下的匹配关系已经非常少了,那么就放弃优化。内点数直接设置为0
if ( nCorrespondences - nBad < 10 ) return 0;
-
-
step 7 再次g2o优化剔除后剩下的边
optimizer.initializeOptimization(); optimizer.optimize(nMoreIterations); -
统计第二次优化后,这些匹配点中是内点的个数
-
遍历所有的pKF2的地图点到pKF1的投影边vpEdges12,for
-
获取正向投影边e12
-
获取反向投影边e21
-
如果e12或e21不存在,则跳过,continue
-
进行卡方检验阈值,如果正向投影或者反向投影任意一个误差超过阈值,则获取边的索引,删除匹配关系;否则,内点数+1
if(e12->chi2()>th2 || e21->chi2()>th2) { size_t idx = vnIndexEdge[i]; vpMatches1[idx]=static_cast<MapPoint*>(NULL); } else nIn++;
-
-
-
step 8 用优化后的结果来更新Sim3位姿
g2o::VertexSim3Expmap* vSim3_recov = static_cast<g2o::VertexSim3Expmap*>(optimizer.vertex(0)); g2oS12= vSim3_recov->estimate(); -
返回内点数
reutrn nIn;
void Optimizer::OptimizeEssentialGraph(Map* pMap, KeyFrame* pLoopKF, KeyFrame* pCurKF,const LoopClosing::KeyFrameAndPose &NonCorrectedSim3,const LoopClosing::KeyFrameAndPose &CorrectedSim3,const map<KeyFrame *, set<KeyFrame *> > &LoopConnections, const bool &bFixScale)
- @brief 闭环检测后,EssentialGraph优化,仅优化所有关键帧位姿,不优化地图点
-
- Vertex:
-
- g2o::VertexSim3Expmap,Essential graph中关键帧的位姿
-
- Edge:
-
- g2o::EdgeSim3(),BaseBinaryEdge
-
- Vertex:关键帧的Tcw,MapPoint的Pw
-
- measurement:经过CorrectLoop函数步骤2,Sim3传播校正后的位姿
-
- InfoMatrix: 单位矩阵
*
- InfoMatrix: 单位矩阵
- @param pMap 全局地图
- @param pLoopKF 闭环匹配上的关键帧
- @param pCurKF 当前关键帧
- @param NonCorrectedSim3 未经过Sim3传播调整过的关键帧位姿
- @param CorrectedSim3 经过Sim3传播调整过的关键帧位姿
- @param LoopConnections 因闭环时地图点调整而新生成的边
步骤:
-
step 1 构造优化器
-
构建线性求解优化器
g2o::BlockSolver_7_3::LinearSolverType * linearSolver = new g2o::LinearSolverEigen<g2o::BlockSolver_7_3::PoseMatrixType>(); -
创建BlockSolver,并使用上面定义的线性求解器初始化
g2o::BlockSolver_7_3 * solver_ptr= new g2o::BlockSolver_7_3(linearSolver); -
创建总求解器solver,使用L-M迭代
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr); -
创建稀疏优化器(SparseOptimizer),
g2o::SparseOptimizer optimizer; optimizer.setVerbose(false); // 第一次迭代的初始lambda值,如未指定会自动计算一个合适的值 solver->setUserLambdaInit(1e-16); optimizer.setAlgorithm(solver)
-
-
设置变量,获取信息
// 获取当前地图中的所有关键帧 和地图点 const vector<KeyFrame*> vpKFs = pMap->GetAllKeyFrames(); const vector<MapPoint*> vpMPs = pMap->GetAllMapPoints(); // 最大关键帧id,用于添加顶点时使用 const unsigned int nMaxKFid = pMap->GetMaxKFid(); // 记录所有优化前关键帧的位姿,优先使用在闭环时通过Sim3传播调整过的Sim3位姿 vector<g2o::Sim3,Eigen::aligned_allocator<g2o::Sim3> > vScw(nMaxKFid+1); // 记录所有关键帧经过本次本质图优化过的位姿 vector<g2o::Sim3,Eigen::aligned_allocator<g2o::Sim3> > vCorrectedSwc(nMaxKFid+1); // 这个变量没有用 vector<g2o::VertexSim3Expmap*> vpVertices(nMaxKFid+1); // 两个关键帧之间共视关系的权重的最小值 const int minFeat = 100; -
step 2 将地图中所有关键帧的位姿作为顶点添加到优化器
尽可能使用经过Sim3 调整的位姿
遍历全局地图中的所有关键帧,for
-
获取一个关键帧
-
如果该帧是坏的,则跳过,continue
-
构建顶点变量
g2o::VertexSim3Expmap* VSim3 = new g2o::VertexSim3Expmap(); -
获取关键帧在所有关键帧中的id,用来设置为顶点的id
-
获取该帧在已经过Sim3 校正的位姿
LoopClosing::KeyFrameAndPose::const_iterator it = CorrectedSim3.find(pKF); if(it!=CorrectedSim3.end()) -
如果该关键帧在闭环时通过Sim3传播调整过,优先用调整后的Sim3位姿;否则用跟踪时的位姿,尺度为1
LoopClosing::KeyFrameAndPose::const_iterator it = CorrectedSim3.find(pKF); if(it!=CorrectedSim3.end()) { // 如果该关键帧在闭环时通过Sim3传播调整过,优先用调整后的Sim3位姿 vScw[nIDi] = it->second; VSim3->setEstimate(it->second); } else { // 如果该关键帧在闭环时没有通过Sim3传播调整过,用跟踪时的位姿,尺度为1 Eigen::Matrix<double,3,3> Rcw = Converter::toMatrix3d(pKF->GetRotation()); Eigen::Matrix<double,3,1> tcw = Converter::toVector3d(pKF->GetTranslation()); g2o::Sim3 Siw(Rcw,tcw,1.0); vScw[nIDi] = Siw; VSim3->setEstimate(Siw); } -
如果该帧为闭环匹配上的帧(认为是准确的,作为基准),则不进行位姿优化。(注意这里并没有锁住第0个关键帧,所以初始关键帧位姿也做了优化)
if( pKF == pLoopKF ) VSim3->setFixed(true); -
设置顶点参数,添加顶点
VSim3->setId(nIDi); VSim3->setMarginalized(false); // 和当前系统的传感器有关,如果是RGBD或者是双目,那么就不需要优化sim3的缩放系数,保持为1即可 VSim3->_fix_scale = bFixScale; // 添加顶点 optimizer.addVertex(VSim3); // 优化前的位姿顶点,后面代码中没有使用 vpVertices[nIDi]=VSim3;
-
-
创建变量sInsertedEdges,保存由于闭环后优化Sim3而出现的新的关键帧和关键帧之间的连接关系,其中id比较小的关键帧在前,id比较大的关键帧在后
set<pair<long unsigned int,long unsigned int> > sInsertedEdges; -
创建7x7的单应矩阵
const Eigen::Matrix<double,7,7> matLambda = Eigen::Matrix<double,7,7>::Identity(); -
step 3 添加第1种边:闭环时因为地图点调整而出现的关键帧间的新连接关系
遍历所有
map<KeyFrame*, set<KeyFrame*> > LoopConnections;(LoopConnections:存储因为闭环地图点调整而新生成的连接关系),for-
获取一个关键帧pKF及其id(nIDi=pKF->mnId)
-
获取与pKF形成新连接关系的关键帧
const set<KeyFrame*> &spConnections = mit->second; -
获取该帧的Sim变换
const g2o::Sim3 Siw = vScw[nIDi]; const g2o::Sim3 Swi = Siw.inverse(); -
对于当前关键帧nIDi而言,遍历每一个新添加的关键帧nIDj连接关系,for
-
获取与当前关键帧具有连接关系的一个帧
const long unsigned int nIDj = (*sit)->mnId; -
如果同时满足下面两个条件,则跳过,continue
// 同时满足下面2个条件的跳过 // 条件1:至少有一个不是pCurKF或pLoopKF // 条件2:共视程度太少(<100),不足以构成约束的边 if((nIDi!=pCurKF->mnId || nIDj!=pLoopKF->mnId) && pKF->GetWeight(*sit)<minFeat) continue; -
通过上面考验的帧有两种情况:
- 1、恰好是当前帧及其闭环帧 nIDi=pC b urKF 并且nIDj=pLoopKF(此时忽略共视程度)
- 2、任意两对关键帧,共视程度大于100
-
获取相连关键帧的位姿
const g2o::Sim3 Sjw = vScw[nIDj] -
得到两个位姿间的Sim3变换
const g2o::Sim3 Sji = Sjw * Swi; -
创建边的变量
g2o::EdgeSim3* e = new g2o::EdgeSim3(); -
设置顶点
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDj))); e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi))); -
设置观测为两个位姿间的变化,Sji内部是经过了Sim调整的观测
e->setMeasurement(Sji); -
设置信息矩阵,信息矩阵是单位阵,说明这类新增加的边对总误差的贡献也都是一样大的
e->information() = matLambda; -
添加边
optimizer.addEdge(e); -
保证id小的在前,大的在后
sInsertedEdges.insert(make_pair(min(nIDi,nIDj),max(nIDi,nIDj)));
-
-
-
step 4 添加跟踪时形成的边、闭环匹配成功形成的边
遍历当前地图中的所有关键帧
-
获取一个关键帧pKF及其对应的id
-
找到该关键帧在未矫正位姿变量NonCorrectedSim3中的位置
LoopClosing::KeyFrameAndPose::const_iterator iti = NonCorrectedSim3.find(pKF); -
如果找到了,则优先使用未经过Sim3传播调整的位姿;否则,说明没找到,则考虑已经经过Sim3传播调整的位姿
if(iti!=NonCorrectedSim3.end()) Swi = (iti->second).inverse(); //优先使用未经过Sim3传播调整的位姿 else Swi = vScw[nIDi].inverse(); //没找到才考虑已经经过Sim3传播调整的位姿 -
获取关键帧pKF的父节点pParentKF
-
step 4.1 添加第二种边:生成树的边(有父关键帧),父关键帧就是和当前帧共视程度最高的关键帧
如果父关键帧pParentKF存在,则
-
获取父关键帧的id
int nIDj=pParentKF->mnId; -
找到父关键帧在未矫正位姿变量NonCorrectedSim3中的位置
LoopClosing::KeyFrameAndPose::const_iterator itj = NonCorrectedSim3.find(pParentKF); -
如果找到了,则优先使用未经过Sim3传播调整的位姿;否则,使用经Sim3调整过的位姿
if(itj!=NonCorrectedSim3.end()) Sjw = itj->second; else Sjw = vScw[nIDj]; -
计算父子关键帧之间的相对位姿
g2o::Sim3 Sji=Sjw*Swi; -
创建边的变量
g2o::EdgeSim3* e=new g2o::EdgeSim3(); -
设置两个顶点
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDj))); e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi))); -
设置初值,希望父子关键帧之间的位姿差最小
e->setMeasurement(Sji); -
设置信息矩阵
e->information() = matLambda; -
添加边
optimizer.addEdge(e);
-
-
step 4.2 添加第三种边:当前帧与闭环匹配帧之间的连接关系(这里面也包括了当前遍历到的这个关键帧之前曾经存在过的回环边)
-
获取和当前关键帧形成闭环关系的关键帧
const set<KeyFrame*> sLoopEdges = pKF->GetLoopEdges(); -
遍历所有和当前关键帧形成闭环关系的关键帧,for
-
获取一个关键帧
KeyFrame pLKF=*sit; -
注意要比当前遍历到的这个关键帧的id小,这个是为了避免重复添加
如果
pLKF->mnId<pKF->mnId,则继续下面的操作 -
找到pLFK在NonCorrectedSim3中的位置itl
LoopClosing::KeyFrameAndPose::const_iterator itl = NonCorrectedSim3.find(pLKF); -
如果找到了,则优先使用未经过Sim3传播调整的位姿;否则,说明没找到,则使用经Sim3调整过的位姿
if(itl!=NonCorrectedSim3.end()) Slw = itl->second; else Slw = vScw[pLKF->mnId]; -
计算两个位姿间的相对变换,创建边的变量,设置两个顶点,将相对位姿作为初值,设置信息矩阵,添加边
g2o::Sim3 Sli = Slw * Swi; g2o::EdgeSim3* el = new g2o::EdgeSim3(); el->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pLKF->mnId))); el->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi))); // 根据两个位姿顶点的位姿算出相对位姿作为边 el->setMeasurement(Sli); el->information() = matLambda; optimizer.addEdge(el);
-
-
-
step 4.3 添加第四种边:共视程度超过100的关键帧也作为边进行优化
-
取出和当前关键帧共视程度超过100的关键帧
const vector<KeyFrame*> vpConnectedKFs = pKF->GetCovisiblesByWeight(minFeat); -
遍历所有的共视关键帧vpConnectedKFs,for
-
获取一个共视关键帧pKFn
-
要避免重复的添加,需要进行判断,需要避免以下情况:最小生成树中的父子关键帧关系,以及和当前遍历到的关键帧构成了回环关系
如果当前帧pKFn存在,且pKFn不等于父关键帧,且pFKn不是pKF的子关键帧,且pKFn不在回环sLoopEdges中,则继续下面的操作
if(pKFn && pKFn!=pParentKF && !pKF->hasChild(pKFn) && !sLoopEdges.count(pKFn)) -
如果该帧不是坏点,该帧的id比pKF的小,则继续下面的操作
if(!pKFn->isBad() && pKFn->mnId<pKF->mnId) -
如果该边已经在第一种情况中添加了,则跳过
if(SInsertedEdges.count(make_pair(min(pKF->mnId,pKFn->mnId),max(pKF->mnId,pKFn->mnId)))) continue; -
获取pKFn在未优化位姿NonCorrectedSim3中的位置,并根据其是否在NonCorrectedSim3中,判断该使用哪个位姿。(优先使用未经过Sim3传播调整的位姿)
g2o::Sim3 Snw; LoopClosing::KeyFrameAndPose::const_iterator itn = NonCorrectedSim3.find(pKFn); // 优先未经过Sim3传播调整的位姿 if(itn!=NonCorrectedSim3.end()) Snw = itn->second; else Snw = vScw[pKFn->mnId]; -
计算相对位姿,创建边的变量,设置顶点,设置初值,设置信息矩阵,添加边
g2o::Sim3 Sni = Snw * Swi; g2o::EdgeSim3* en = new g2o::EdgeSim3(); en->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pKFn->mnId))); en->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi))); en->setMeasurement(Sni); en->information() = matLambda; optimizer.addEdge(en);
-
-
-
-
step 5 开始g2o优化,迭代20次
optimizer.initializeOptimization(); optimizer.optimize(20); -
更新地图前,先上锁,防止冲突
unique_lock<mutex> lock(pMap->mMutexMapUpdate); -
step 6 将优化后的位姿更新到关键帧中
遍历地图中的所有关键帧
-
获取关键帧及其id
KeyFrame* pKFi = vpKFs[i]; const int nIDi = pKFi->mnId; -
根据id获取经过优化后的顶点
g2o::VertexSim3Expmap* VSim3 = static_cast<g2o::VertexSim3Expmap*>(optimizer.vertex(nIDi)); -
根据顶点得到矫正后的Sim3变换
g2o::Sim3 CorrectedSiw = VSim3->estimate(); -
记录经过优化后的Sim3位姿
vCorrectedSwc[nIDi]=CorrectedSiw.inverse(); -
获取旋转、平移和尺度
Eigen::Matrix3d eigR = CorrectedSiw.rotation().toRotationMatrix(); Eigen::Vector3d eigt = CorrectedSiw.translation(); double s = CorrectedSiw.scale(); -
转换尺度为1的变换矩阵的形式,即Sim3->SE
eigt *=(1./s); //[R t/s;0 1] cv::Mat Tiw = Converter::toCvSE3(eigR,eigt); -
将更新的位姿写入到关键帧中
pKFi->SetPose(Tiw);
-
-
step 7 步骤5和步骤6优化得到关键帧的位姿后,地图点根据参考帧优化前后的相对关系调整自己的位姿
遍历所有地图点,for
-
获取一个地图点
-
如果该地图点时坏的,则跳过,continue
-
如果该地图点在闭环检测中被当前KF调整过,那么使用调整它的KF的id;否则,通常情况下地铁点的参考关键帧就是创建该地图点的那个关键帧
if(pMP->mnCorrectedByKF==pCurKF->mnId) { nIDr = pMP->mnCorrectedReference; } else { // 通常情况下地图点的参考关键帧就是创建该地图点的那个关键帧 KeyFrame* pRefKF = pMP->GetReferenceKeyFrame(); nIDr = pRefKF->mnId; } -
得到地图点参考关键帧优化前的位姿
g2o::Sim3 Srw = vScw[nIDr]; -
得到地图点参考关键帧优化后的位姿
g2o::Sim3 correctedSwr = vCorrectedSwc[nIDr]; -
得到地图点的世界坐标,得到的坐标为Mat型
cv::Mat P3Dw = pMP->GetWorldPos(); -
将坐标转化为3x1的矩阵
Eigen::Matrix<double,3,1> eigP3Dw = Converter::toVector3d(P3Dw); -
根据相对位姿变换,求取更新后的地图点坐标
Eigen::Matrix<double,3,1> eigCorrectedP3Dw = correctedSwr.map(Srw.map(eigP3Dw)); -
将更新后的地图点坐标转换为Mat型
cv::Mat cvCorrectedP3Dw = Converter::toCvMat(eigCorrectedP3Dw); -
更新地图点坐标
pMP->SetWorldPos(cvCorrectedP3Dw); -
更新地图点的平均观测方向、观测距离范围
pMP->UpdateNormalAndDepth();
-
void Optimizer::BundleAdjustment(const vector<KeyFrame *> &vpKFs, const vector<MapPoint > &vpMP, int nIterations, bool pbStopFlag, const unsigned long nLoopKF, const bool bRobust)
- @brief bundle adjustment 优化过程
-
- Vertex: g2o::VertexSE3Expmap(),即当前帧的Tcw
- g2o::VertexSBAPointXYZ(),MapPoint的mWorldPos
-
- Edge:
-
- g2o::EdgeSE3ProjectXYZ(),BaseBinaryEdge
-
- Vertex:待优化当前帧的Tcw
-
- Vertex:待优化MapPoint的mWorldPos
-
- measurement:MapPoint在当前帧中的二维位置(u,v)
-
- InfoMatrix: invSigma2(与特征点所在的尺度有关)
- @param[in] vpKFs 参与BA的所有关键帧
- @param[in] vpMP 参与BA的所有地图点
- @param[in] nIterations 优化迭代次数
- @param[in] pbStopFlag 外部控制BA结束标志
- @param[in] nLoopKF 形成了闭环的当前关键帧的id
- @param[in] bRobust 是否使用核函数
步骤:
-
创建变量,记录不参与优化的地图点
vector<bool> vbNotIncludedMP; vbNotIncludedMP.resize(vpMP.size()); -
step 1 初始化g2o优化器
g2o::SparseOptimizer optimizer; g2o::BlockSolver_6_3::LinearSolverType * linearSolver; linearSolver = new g2o::LinearSolverEigen<g2o::BlockSolver_6_3::PoseMatrixType>(); g2o::BlockSolver_6_3 * solver_ptr = new g2o::BlockSolver_6_3(linearSolver); // 使用LM算法优化 g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr); optimizer.setAlgorithm(solver); -
如果这个时候外部请求终止,那就结束(注意这句指向之后,外部再请求结束BA,就结束不了了)
if(pbStopFlag) optimizer.setForceStopFlag(pbStopFlag); -
记录添加到优化器中的顶点的最大关键帧id
long unsigned int maxKFid = 0 ; -
step 2 向优化器添加顶点
-
step 2.1 向优化器添加关键帧位姿顶点
遍历当前地图中的所有关键帧vpKFs,for
-
获取一个关键帧pKF
KeyFrame* pKF = vpKFs[i]; -
如果该帧是无效关键帧,则跳过,continue
-
对于每一个能用的关键帧构造SE3顶点,其实就是当前关键帧的位姿
g2o::VertexSE3Expmap * vSE3 = new g2o::VertexSE3Expmap(); vSE3->setEstimate(Converter::toSE3Quat(pKF->GetPose())); -
顶点的id就是关键帧在所有关键帧中的id
vSE3->setId(pKF->mnId); -
只有第0帧关键帧不优化(参考基准)
vSE3->setFixed(pKF->mnId==0); -
向优化器中添加顶点,并且更新maxKFid
optimizer.addVertex(vSE3); -
记录最大的id
if(pKF->mnId>maxKFid) maxKFid=pKF->mnId;
-
-
设置阈值(卡方分布95%以上可信度的时候的阈值)
const float thHuber2D = sqrt(5.99); // 自由度为2 const float thHuber3D = sqrt(7.815); // 自由度为3 -
step 2.2 向优化器添加地图点作为顶点
遍历地图中的所有地图点vpMP,for
-
获取地图点
-
如果地图点无效,则跳过,continue
-
创建顶点
g2o::VertexSBAPointXYZ* vPoint = new g2o::VertexSBAPointXYZ(); -
设置初始值,注意由于地图点的位置是使用cv::Mat数据类型表示的,这里需要转换成为Eigen::Vector3d类型
vPoint->setEstimate(Converter::toVector3d(pMP->GetWorldPos())); -
设置id,前面记录的maxKFid在这里使用
const int id = pMP->mnId+maxKFid+1; vPoint->setId(id); -
注意g2o在做BA的优化时必须将其所有地图点全部schur掉,否则会出错。原因是使用了
g2o::LinearSolver < BalBlockSolver::PoseMatrixType>这个类型来指定linearsolver,其中模板参数当中的位姿矩阵类型在程序中为相机姿态参数的维度,于是BA当中schur消元后解得线性方程组必须是只含有相机姿态变量。Ceres库则没有这样的限制. -
设置边缘化,添加顶点
vPoint->setMarginalized(true); optimizer.addVertex(vPoint); -
取出地图点和关键帧之间观测的关系
const map<KeyFrame*,size_t> observations = pMP->GetObservations(); -
统计边的数量
int nEdges=0; -
step 3 向优化器中添加投影边(是在遍历地图点、添加地图点的顶点的时候顺便添加的)
遍历观测到当前地图点的所有关键帧observations,for
-
获取关键帧
-
如果该关键帧不合法,则跳过,continue
-
边数加1
nEdges++; -
取出地图点对应该关键帧的2D特征点
const cv::KeyPoint &kpUn = pKF->mvKeysUn[mit->second]; -
如果是单目模式,则
-
构造观测
Eigen::Matrix<double,2,1> obs; obs << kpUn.pt.x, kpUn.pt.y; -
创建边
g2o::EdgeSE3ProjectXYZ* e = new g2o::EdgeSE3ProjectXYZ(); -
边连接的第0号顶点对应的是第id个地图点
e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id))); -
边连接的第1号顶点对应的是第id个关键帧
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pKF->mnId))); -
设置初值
e->setMeasurement(obs); -
设置信息矩阵。
信息矩阵,也是协方差,表明了这个约束的观测在各个维度(x,y)上的可信程度,在我们这里对于具体的一个点,两个坐标的可信程度都是相同的,其可信程度受到特征点在图像金字塔中的图层有关,图层越高,可信度越差。为了避免出现信息矩阵中元素为负数的情况,这里使用的是sigma^(-2)
const float &invSigma2 = pKF->mvInvLevelSigma2[kpUn.octave]; e->setInformation(Eigen::Matrix2d::Identity()*invSigma2); -
如果要使用鲁棒核函数,则
if(bRobust) { g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber; e->setRobustKernel(rk); // 这里的重投影误差,自由度为2,所以这里设置为卡方分布中自由度为2的阈值,如果重投影的误差大约大于1个像素的时候,就认为不太靠谱的点了, // 核函数是为了避免其误差的平方项出现数值上过大的增长 rk->setDelta(thHuber2D); } -
设置相机内参
-
添加边
optimizer.addEdge(e);
-
-
如果是双目或RGBD相机,则
-
双目的观测数据由三个部分组成:投影点的x坐标,投影点的y坐标,以及投影点在右目中的x坐标(默认y方向上已经对齐了)
Eigen::Matrix<double,3,1> obs; const float kp_ur = pKF->mvuRight[mit->second]; obs << kpUn.pt.x, kpUn.pt.y, kp_ur -
对于双目输入,g2o也有专门的误差边
g2o::EdgeStereoSE3ProjectXYZ* e = new g2o::EdgeStereoSE3ProjectXYZ(); -
设置顶点和观测
e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id))); e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pKF->mnId))); e->setMeasurement(obs); -
设置信息矩阵,信息矩阵这里是相同的,考虑的是左目特征点的所在图层
const float &invSigma2 = pKF->mvInvLevelSigma2[kpUn.octave]; Eigen::Matrix3d Info = Eigen::Matrix3d::Identity()*invSigma2; e->setInformation(Info); -
如果要使用鲁棒核函数,则
if(bRobust) { g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber; e->setRobustKernel(rk); // 由于现在的观测有三个值,重投影误差会有三个平方项的和组成,因此对应的卡方分布的自由度为3,所以这里设置的也是自由度为3的时候的阈值 rk->setDelta(thHuber3D); } -
填充相机的基本参数,除了内参还有pKF->mbf
-
添加边
optimizer.addEdge(e);
-
-
-
如果因为一些特殊原因,实际上并没有任何关键帧观测到当前的这个地图点,那么就删除掉这个顶点,并且这个地图点也就不参与优化
if(nEdges==0) { optimizer.removeVertex(vPoint); vbNotIncludedMP[i]=true; } else { vbNotIncludedMP[i]=false; }
-
-
-
step 4 开始优化
optimizer.initializeOptimization(); optimizer.optimize(nIterations); -
step 5 得到优化的结果
-
step 5.1 遍历所有的关键帧vpKFs,for
-
获取关键帧
-
如果该关键帧无效,则跳过,continue
-
获取到优化后的位姿
g2o::VertexSE3Expmap* vSE3 = static_cast<g2o::VertexSE3Expmap*>(optimizer.vertex(pKF->mnId)); g2o::SE3Quat SE3quat = vSE3->estimate(); -
原则上来讲不会出现"当前闭环关键帧是第0帧"的情况,如果这种情况出现,只能够说明是在创建初始地图点的时候调用的这个全局BA函数。这个时候,地图中就只有两个关键帧,其中优化后的位姿数据可以直接写入到帧的成员变量中;如果不是第0帧,则是正常的操作,先把优化后的位姿写入到帧的一个专门的成员变量mTcwGBA中备用
if(nLoopKF==0) { // 原则上来讲不会出现"当前闭环关键帧是第0帧"的情况,如果这种情况出现,只能够说明是在创建初始地图点的时候调用的这个全局BA函数. // 这个时候,地图中就只有两个关键帧,其中优化后的位姿数据可以直接写入到帧的成员变量中 pKF->SetPose(Converter::toCvMat(SE3quat)); } else { // 正常的操作,先把优化后的位姿写入到帧的一个专门的成员变量mTcwGBA中备用 pKF->mTcwGBA.create(4,4,CV_32F); Converter::toCvMat(SE3quat).copyTo(pKF->mTcwGBA); pKF->mnBAGlobalForKF = nLoopKF; }
-
-
step 5.2 遍历所有的地图点vpMP,去除其中没有参与优化过程的地图点,for
-
如果该点是不参与优化的地图点,则跳过,continue
-
获取地图点
-
如果该地图点无效,则跳过,continue
-
获取优化之后的地图点位置
g2o::VertexSBAPointXYZ* vPoint = static_cast<g2o::VertexSBAPointXYZ*>(optimizer.vertex(pMP->mnId+maxKFid+1)); -
和上面对关键帧的操作一样,如果这个GBA是在创建初始地图的时候调用的话,那么地图点的位姿也可以直接写入;反之,如果是正常的闭环过程调用,就先临时保存一下
// 和上面对关键帧的操作一样 if(nLoopKF==0) { // 如果这个GBA是在创建初始地图的时候调用的话,那么地图点的位姿也可以直接写入 pMP->SetWorldPos(Converter::toCvMat(vPoint->estimate())); pMP->UpdateNormalAndDepth(); } else { // 反之,如果是正常的闭环过程调用,就先临时保存一下 pMP->mPosGBA.create(3,1,CV_32F); Converter::toCvMat(vPoint->estimate()).copyTo(pMP->mPosGBA); pMP->mnBAGlobalForKF = nLoopKF; }// 判断是因为什么原因调用的GBA
-
-
ORBextractor.h
参数:
函数:
ORBmatcher.h
参数:

函数:
int ORBmatcher::SearchByProjection(Frame &CurrentFrame, const Frame &LastFrame, const float th, const bool bMono)
- 用于恒速模型跟踪,用前一个普通帧投影到当前帧中进行匹配
- @brief 将上一帧跟踪的地图点投影到当前帧,并且搜索匹配点。用于跟踪前一帧
- 步骤
- Step 1 建立旋转直方图,用于检测旋转一致性
- Step 2 计算当前帧和前一帧的平移向量
- Step 3 对于前一帧的每一个地图点,通过相机投影模型,得到投影到当前帧的像素坐标
- Step 4 根据相机的前后前进方向来判断搜索尺度范围
- Step 5 遍历候选匹配点,寻找距离最小的最佳匹配点
- Step 6 计算匹配点旋转角度差所在的直方图
- Step 7 进行旋转一致检测,剔除不一致的匹配
- @param[in] CurrentFrame 当前帧
- @param[in] LastFrame 上一帧
- @param[in] th 搜索范围阈值,默认单目为7,双目15
- @param[in] bMono 是否为单目
- @return int 成功匹配的数量
int ORBmatcher::SearchByProjection(Frame &F, const vector<MapPoint*> &vpMapPoints, const float th)
- 用于局部地图点跟踪,用所有局部地图点通过投影进行特征点匹配
- @brief 通过投影地图点到当前帧,对Local MapPoint进行跟踪,找到所有有效的局部地图点
- 步骤
- Step 1 遍历有效的局部地图点
- Step 2 设定搜索搜索窗口的大小。取决于视角, 若当前视角和平均视角夹角较小时, r取一个较小的值
- Step 3 通过投影点以及搜索窗口和预测的尺度进行搜索, 找出搜索半径内的候选匹配点索引
- Step 4 寻找候选匹配点中的最佳和次佳匹配点
- Step 5 筛选最佳匹配点
- @param[in] F 当前帧
- @param[in] vpMapPoints 局部地图点,来自局部关键帧
- @param[in] th 搜索范围
- @return int 成功匹配的数目
int ORBmatcher::SearchByProjection(KeyFrame* pKF, cv::Mat Scw, const vector<MapPoint*> &vpPoints, vector<MapPoint*> &vpMatched, int th)
- @brief 根据Sim3变换,将闭环KF及其共视KF的所有地图点(不考虑当前KF已经匹配的地图点)投影到当前KF,生成新的匹配点对
- @param[in] pKF 当前KF
- @param[in] Scw 当前KF和闭环KF之间的Sim3变换
- @param[in] vpPoints 闭环KF及其共视KF的地图点
- @param[in] vpMatched 当前KF的已经匹配的地图点
- @param[in] th 搜索范围
- @return int 返回新的成功匹配的点对的数目
步骤:
-
获取当前帧pKF 的相机内参
-
step 1 分解Sim变换矩阵。(这里的尺度在Pc归一化时会被约掉。可以理解为投影的时候不需要尺度,因为变换到了射线上,尺度无关,尺度会在后面优化的时候用到)
- 通过Sim的变换矩阵Scw,得到尺度s
- 计算旋转矩阵,保证旋转矩阵行列式为1
- 计算去掉尺度后的平移向量
- 计算世界坐标系下相机光心坐标
- 使用set类型,记录前面已经成功的匹配关系,避免重复匹配。并去除其中无效匹配关系(NULL)
-
Step 2 遍历闭环KF及其共视KF的所有地图点(不考虑当前KF已经匹配的地图点)投影到当前KF
遍历闭环关键帧及其共视关键帧的所有地图点,for
-
获取地图点信息
-
step 2.1 如果该地图点是坏点或者当前KF已经匹配上的地图点,则跳过
-
step 2.2 投影到当前KF的图像坐标并判断是否有效
- 获取该地图点的世界坐标
- 通过R和t计算其相机坐标
- 如果深度值不为正,则跳过,continue
- 根据相机内参,将其投影到当前帧pKF下,得到其二维坐标
- 判断投影点是否在图像范围内,如果不在,则跳过,continue
- 获取地图点的对应的最大最小距离的阈值,计算地图点到相机光心的距离
- 判断距离是否在有效距离内,如果不在,则跳过continue
- 如果观测角度不小于60°(角度由平均观测方向和光心坐标求得),则跳过,continue
- 根据当前这个地图点距离当前KF光心的距离,预测该点在当前KF中的尺度(图层)
- 根据尺度确定搜索半径
-
step 2.3 搜索候选匹配点
- 根据投影点的二维坐标和搜索半径,找到pKF对应图像中该区域的候选匹配点
- 如果没找到候选匹配点,则跳过continue
- 获取地图点的描述子
-
step 2.4 遍历候选匹配点,找到最佳匹配点(这一步在很多函数中都出现过)
开始遍历,for
- 如果该点已经匹配过,则跳过,continue
- 获取该点的尺度
- 如果不在一个尺度,则跳过,continue
- 获取该点对应的描述子
- 计算描述子距离
- 比较距离大小,找到最佳匹配点的描述子距离和索引
-
如果最佳匹配点的描述子距离小于阈值,则该MapPoint与bestIdx对应的特征点匹配成功,记录匹配成功的点对数
-
-
step 3 返回新的成功匹配的点对数目
int ORBmatcher::SearchByProjection(Frame &CurrentFrame, KeyFrame pKF, const set<MapPoint> &sAlreadyFound, const float th , const int ORBdist)
- 用于重定位跟踪,将候选关键帧中未匹配的地图点投影到当前帧中,生成新的匹配
- @brief 通过投影的方式将关键帧中未匹配的地图点投影到当前帧中,进行匹配,并通过旋转直方图进行筛选
- @param[in] CurrentFrame 当前帧
- @param[in] pKF 参考关键帧
- @param[in] sAlreadyFound 已经找到的地图点集合,不会用于PNP
- @param[in] th 匹配时搜索范围,会乘以金字塔尺度
- @param[in] ORBdist 匹配的ORB描述子距离应该小于这个阈值
- @return int 成功匹配的数量
步骤:
- 获取当前帧世界坐标系到相机坐标系的变换矩阵,Rcw、tcw 、Ow= -Rcw.t()*tcw ( Ow为光心坐标系 )
- 建立旋转直方图,用于检测旋转一致性
- 遍历关键帧中的每一个地图点,通过相机投影模型,得到投影到当前帧的像素坐标
- 如果 地图点存在 并且 不在已有地图点集合里 ,则继续下一步
- 获取地图点的世界坐标,并将其投影到当前帧坐标
- 计算地图点到光心的距离,判断距离是否符合图像金字塔的要求
- 根据距离预测尺度(图像金字塔的层数)
- 搜索半径和尺度相关,根据尺度,求解搜索半径
- 搜索候选匹配点GetFeaturesInArea( )
- 获取当前地图点的描述子
- 遍历候选匹配点,寻找距离最小的最佳匹配点
- 若当前候选匹配点已存在地图点,则continue
- 获取当前候选匹配点对应的描述子
- 计算两个描述子之间的距离
- 找到最小描述子对应的最佳匹配点
- if(bestDist<=ORBdist)
- 记录当前帧最佳匹配点的索引对应的地图点 CurrentFrame.mvpMapPoints[bestIdx2]=pMP
- 计算匹配点旋转角度差所在的直方图
- 进行旋转一致检测,剔除不一致的匹配
float ORBmatcher::RadiusByViewingCos(const float &viewCos)
// 根据观察的视角来计算匹配的时的搜索窗口大小
{
// 当视角相差小于3.6°,对应cos(3.6°)=0.998,搜索范围是2.5,否则是4
if(viewCos>0.998)
return 2.5;
else
return 4.0;
}
bool ORBmatcher::CheckDistEpipolarLine(const cv::KeyPoint &kp1,const cv::KeyPoint &kp2,const cv::Mat &F12,const KeyFrame* pKF2)
- @brief 用基础矩阵检查极线距离是否符合要求
- @param[in] kp1 KF1中特征点
- @param[in] kp2 KF2中特征点
- @param[in] F12 从KF2到KF1的基础矩阵
- @param[in] pKF2 关键帧KF2
- @return true
- @return false
步骤:
- Step 1 求出kp1在pKF2上对应的极线。Epipolar line in second image l2 = x1’F12 = [a b c]
- Step 2 计算kp2特征点到极线l2的距离。极线l2:ax + by + c = 0 。(u,v)到l2的距离为: |au+bv+c| / sqrt(a2+b2)
- Step 3 判断误差是否满足条件。尺度越大,误差范围应该越大。 金字塔最底层一个像素就占一个像素,在倒数第二层,一个像素等于最底层1.2个像素(假设金字塔尺度为1.2)。 3.84 是自由度为1时,服从高斯分布的一个平方项(也就是这里的误差)小于一个像素,这件事发生概率超过95%时的概率 (卡方分布)。
int ORBmatcher::SearchByBoW(KeyFrame* pKF,Frame &F, vector<MapPoint*> &vpMapPointMatches)
- @brief 通过词袋,对关键帧的特征点进行跟踪。在这里面使用了词袋加速(其实是对同一节点下的特征点计算描述子,避免对所有的描述子遍历,以此做到加速)(主要是将关键帧中的特征点与当前帧的特征点进行匹配,同时找到当前帧特征点对应的地图点)
- 步骤
- Step 1:分别取出属于同一node的ORB特征点(只有属于同一node,才有可能是匹配点)
- Step 2:遍历KF中属于该node的特征点
- Step 3:遍历F中属于该node的特征点,寻找最佳匹配点
- Step 4:根据阈值 和 角度投票剔除误匹配
- Step 5:根据方向剔除误匹配的点
- @param pKF 关键帧
- @param F 当前普通帧
- @param vpMapPointMatches F中地图点对应的匹配,NULL表示未匹配
- @return 成功匹配的数量
步骤:
- 初始获取所有信息,获取该关键帧的地图点、取出关键帧的词袋特征向量、特征点角度旋转差统计用的直方图、将属于同一结点(特定层)的ORB特征进行匹配
- 开始循环while
- 分别取出属于同一node的ORB特征点(只有属于同一node,才有可能是匹配点)
- 获取关键帧和当前帧中所有在该node下的特征点索引
- 遍历KF中属于该node的特征点(在这一步中当前帧中的点是暂时没有用地图点,而是关键帧的地图点起到作用(关键帧的地图点起到记录当前帧的特征点是否也会对应这个地图点,主要是找到当前帧的特征点对应的地图点))
- 获取关键帧该节点中特征点的索引,然后取出KF中该特征对应的地图点
- 判断地图点是否符合要求
- 取出KF中该特征对应的描述子,用于后续计算
- 遍历F中属于该node的特征点,寻找最佳匹配点
- 获取当前帧该节点中特征点的索引
- 如果地图点存在,说明这个点已经被匹配过了,不再匹配,加快速度
- 取出F中该特征对应的描述子
- 计算KF和F中两点的描述子的距离
- 记录最佳距离、最佳距离对应的索引、次佳距离等
- 根据阈值 和 角度投票剔除误匹配
- 第一关筛选:匹配距离必须小于设定阈值
- 第二关筛选:最佳匹配比次佳匹配明显要好,那么最佳匹配才真正靠谱
- 记录成功匹配特征点的对应的地图点(来自关键帧)
- 计算匹配点旋转角度差所在的直方图
- angle:每个特征点在提取描述子时的旋转主方向角度,如果图像旋转了,这个角度将发生改变。 所有的特征点的角度变化应该是一致的,通过直方图统计得到最准确的角度变化值
- 该特征点的角度变化值rot。将rot分配到bin组, 四舍五入, 其实就是离散到对应的直方图组中
- 若不同,就按照b、c进行对齐操作 else if(KFit->first < Fit->first),则KFit = vFeatVecKF.lower_bound(Fit->first);
- else Fit = F.mFeatVec.lower_bound(KFit->first);
- 分别取出属于同一node的ORB特征点(只有属于同一node,才有可能是匹配点)
- 根据方向剔除误匹配的点
- 筛选出在旋转角度差落在在直方图区间内数量最多的前三个bin的索引
- 遍历所有特征点,若如果特征点的旋转角度变化量属于这三个组,则保留;否之,则剔除掉不在前三的匹配对,因为他们不符合“主流旋转方向”
int ORBmatcher::Fuse(KeyFrame *pKF, const vector<MapPoint *> &vpMapPoints, const float th)
- @brief 将地图点投影到关键帧中进行匹配和融合;融合策略如下
- 1.如果地图点能匹配关键帧的特征点,并且该点有对应的地图点,那么选择观测数目多的替换两个地图点
- 2.如果地图点能匹配关键帧的特征点,并且该点没有对应的地图点,那么为该点添加该投影地图点
- @param[in] pKF 关键帧
- @param[in] vpMapPoints 待投影的地图点
- @param[in] th 搜索窗口的阈值,默认为3
- @return int 更新地图点的数量
步骤:
- 取出当前帧位姿、内参、光心在世界坐标系下坐标
- 遍历所有待投影地图点(以一个为例)
- 判断地图点的有效性。若无效,则跳过;若有效,则获取地图点的坐标,并将其变换到关键帧的相机坐标系下(深度值应为正)。
- 根据相机内参,将地图点投影到关键帧的图像坐标
- 根据地图点的世界坐标和相机光心坐标,计算地图点到关键帧相机光心距离,并判断是否有效。(用到MapPoint::UpdateNormalAndDepth()中计算的最大最小距离)
- 地图点到光心的连线与该地图点的平均观测向量之间夹角要小于60° (判断语句)。然后根据地图点到相机光心距离预测匹配点所在的金字塔尺度,确定搜索范围。
- 在投影点附近搜索窗口内找到候选匹配点的索引
- 遍历寻找最佳匹配点
- 遍历搜索范围内的features
- 计算投影点与候选匹配特征点的距离,如果偏差很大,直接跳过(这里分为单目和双目两种情况考虑)(主要是计算误差,然后进行卡方检验阈值)
- 计算地图点和候选匹配特征点之间描述子距离
- 选择距离最小的点,即为最佳匹配特征点
- 找到投影点对应的最佳匹配特征点,根据是否存在地图点来融合或新增,(首先判断最佳匹配距离要小于阈值)
- 如果最佳匹配点有对应有效地图点,选择被观测次数最多的那个替换
- 如果最佳匹配点没有对应地图点,添加观测信息
int ORBmatcher::Fuse(KeyFrame *pKF, cv::Mat Scw, const vector<MapPoint *> &vpPoints, float th, vector<MapPoint *> &vpReplacePoint)
- @brief 闭环矫正中使用。将当前关键帧闭环匹配上的关键帧及其共视关键帧组成的地图点投影到当前关键帧,融合地图点
- @param[in] pKF 当前关键帧
- @param[in] Scw 当前关键帧经过闭环Sim3 后的世界到相机坐标系的Sim变换
- @param[in] vpPoints 与当前关键帧闭环匹配上的关键帧及其共视关键帧组成的地图点
- @param[in] th 搜索范围系数
- @param[out] vpReplacePoint 替换的地图点
- @return int 融合(替换和新增)的地图点数目
步骤:
- 获取内参
- step 1 将Sim3 转化为SE3并分解(实际是去掉尺度s),然后计算光心坐标
- 获得当前关键帧已有的地图点spAlreadyFound
- 获得与当前帧闭环匹配上的关键帧及其共视关键帧组成的地图点(vpPoints)的个数
- 遍历vpPoints中的所有地图点,for
- 如果该地图点无效或者已经是该帧的地图点(无需融合),跳过
- step 2 地图点变换到当前相机坐标系下
- 获取当前地图点的位姿
- 根据Rcw、tcw将其变换到相机坐标系下
- 如果深度值小于0,则跳过该点
- step 3 得到地图点投影到当前帧的图像坐标
- 根据内参计算二维图像坐标
- 如果投影点不在图像范围内,则跳过
- step 4 根据距离是否在图像合理金字塔尺度范围内和观测角度是否小于60度判断该地图点是否有效
- 得到地图点的距离合法范围
- 计算地图点距离圆心的距离
- 如果距离不合法,则跳过
- 计算平均观测方向
- 计算观测角度,如果角度大于60度,则跳过
- 根据距离计算其金字塔尺度,然后计算搜索范围
- step 5 在当前帧内根据二维坐标和搜索范围计算搜索匹配候选点
- 如果没有找到匹配候选点,则跳过
- step 6 对每一个候选匹配点都判断金字塔尺度是否一致,然后计算描述子距离,找到最佳匹配点
- step 7 替换或新增地图点
- 如果最佳距离小于阈值,则
- 获取最佳匹配点对应的地图点
- 如果其对应的地图点存在,则
- 如果该点不是坏点,则先记录要替换点的信息,之后再进行替换。(这里不能直接替换,原因是需要对地图点加锁后才能替换,否则可能会crash。所以先记录,在加锁后替换)
- 如果该地图点不存在,则直接添加
- 融合(替换和新增)的地图点数目加1
- 如果最佳距离小于阈值,则
- 返回融合(替换和新增)的地图点数目
int ORBmatcher::SearchBySim3(KeyFrame *pKF1, KeyFrame pKF2, vector<MapPoint> &vpMatches12, const float &s12, const cv::Mat &R12, const cv::Mat &t12, const float th)
- @brief 通过Sim3变换,搜索两个关键帧中更多的匹配点对
- (之前使用SearchByBoW进行特征点匹配时会有漏匹配)
- @param[in] pKF1 当前帧
- @param[in] pKF2 闭环候选帧
- @param[in] vpMatches12 i表示匹配的pKF1 特征点索引,vpMatches12[i]表示匹配的pKF2中地图点,null表示没有匹配
- @param[in] s12 pKF2 到 pKF1 的Sim 变换中的尺度
- @param[in] R12 pKF2 到 pKF1 的Sim 变换中的旋转矩阵
- @param[in] t12 pKF2 到 pKF1 的Sim 变换中的平移向量
- @param[in] th 搜索窗口的倍数
- @return int 新增的匹配点对数目
步骤:
-
Step 1: 准备工作:内参,计算Sim3的逆
- 获取内参
- 获取从world到camera1的变换
- 获取从world到camera2的变换
- 计算Sim3 的逆
- 分别取出两关键帧中的地图点
- 创建vector < bool>类型的变量,记录pKF1,pKF2中已经匹配的特征点,已经匹配记为true,否则false
-
Step 2:记录已经匹配的特征点
for(int i=0; i<N1; i++) { MapPoint* pMP = vpMatches12[i]; if(pMP) { // pKF1中第i个特征点已经匹配成功 vbAlreadyMatched1[i]=true; // 得到该地图点在关键帧pkF2 中的id int idx2 = pMP->GetIndexInKeyFrame(pKF2); if(idx2>=0 && idx2<N2) // pKF2中第idx2个特征点在pKF1中有匹配 vbAlreadyMatched2[idx2]=true; } } -
Step 3:通过Sim变换,寻找 pKF1 中特征点和 pKF2 中的新的匹配。之前使用SearchByBow进行特征点匹配时会有漏匹配。
先以当前帧为例,遍历当前帧的所有特征点,for
-
获取该特点对应的地图点
-
如果该地图点存在或者该特征点已经有匹配点,则跳过continue
-
如果地图点时坏的,则跳过continue
-
Step 3.1 :通过Sim变换,将pKF1的地图点投影到pKF2中的像素坐标(这里的变换矩阵是由Sim变换得到的)
- 获取地图点的世界坐标
- 将pKF1的地图点从world坐标系变换到camera1坐标系
- 再通过Sim3将该地图点从camera1变换到camera2坐标系
- 如果深度值为负,则跳过
- 将其根据内参投影到camera2图像坐标(u,v)
- 如果投影点不在pKF2对应的图像范围内,则跳过
- 如果深度值不在有效范围内,则跳过
-
Step 3.2:预测投影的点在图像金字塔哪一层 (根据深度值进行预测),然后根据层数计算特征点搜索半径
-
Step 3.3:搜索pKF2 中该区域内的所有候选匹配特征点,如果没有匹配到特征点,则跳过
-
获取当前地图点的描述子
-
Step 3.4:遍历所有候选匹配特征点,寻找最佳匹配点(并未使用次佳最佳比例约束)
开始遍历所有候选特征点,for
-
获取特征点
-
如果该特征点所在层级小于投影点层级-1,或者大于投影点层级,则跳过该特征点
if(kp.octave<nPredictedLevel-1 || kp.octave>nPredictedLevel) continue; -
获取该候选特征点对应的描述子
-
计算两描述子距离
-
找到并记录距离最小的点的索引
-
-
如果最佳描述子距离小于阈值,则认为找到匹配点
-
-
Step 4:通过Sim变换,寻找 pKF2 中特征点和 pKF1 中的新的匹配,具体步骤同上Step 3
-
Step 5: 一致性检查,只有在两次互相匹配中都出现才能够认为是可靠的匹配,只有可靠的匹配,才能更新匹配关系
int ORBmatcher::SearchForTriangulation(KeyFrame *pKF1, KeyFrame *pKF2, cv::Mat F12, vector<pair<size_t, size_t> > &vMatchedPairs, const bool bOnlyStereo)
- @brief 利用基础矩阵F12极线约束,用BoW加速匹配两个关键帧的未匹配的特征点,产生新的匹配点对
- 具体来说,pKF1图像的每个特征点与pKF2图像同一node节点的所有特征点依次匹配,判断是否满足对极几何约束,满足约束就是匹配的特征点
- @param pKF1 关键帧1
- @param pKF2 关键帧2
- @param F12 从2到1的基础矩阵
- @param vMatchedPairs 存储匹配特征点对,特征点用其在关键帧中的索引表示
- @param bOnlyStereo 在双目和rgbd情况下,是否要求特征点在右图存在匹配
- @return 成功匹配的数量
步骤:
-
step 1 计算KF1 的相机中心在KF2 图像平面的二维像素坐标
- 获取KF1相机光心在世界坐标系坐标Cw
- 获取KF2相机位姿R2w,t2w,是世界坐标系到相机坐标系
- KF1的相机光心转化到KF2坐标系中的坐标
- 得到KF1的相机光心在KF2中的坐标,也叫极点,这里是像素坐标
- 初始化匹配时的变量和旋转直方图变量
-
Step 2 利用BoW加速匹配:只对属于同一节点(特定层)的ORB特征进行匹配
// FeatureVector其实就是一个map类,那就可以直接获取它的迭代器进行遍历 // FeatureVector的数据结构类似于:{(node1,feature_vector1) (node2,feature_vector2)...} // f1it->first对应node编号,f1it->second对应属于该node的所有特特征点编号 DBoW2::FeatureVector::const_iterator f1it = vFeatVec1.begin(); DBoW2::FeatureVector::const_iterator f2it = vFeatVec2.begin(); DBoW2::FeatureVector::const_iterator f1end = vFeatVec1.end(); DBoW2::FeatureVector::const_iterator f2end = vFeatVec2.end();-
step 2.1 : 遍历pKF1 和pKF2 中的节点 ,当两个都没指向结尾时,一直循环
while(f1it!=f1end && f2it!=f2end)-
如果f1it和f2it属于同一个node节点,则才会进行匹配,这就是BoW加速匹配原理
-
step 2.2:遍历属于同一node节点
(id:f1it->first)下的所有特征点,for,以一个点为例-
获取PKF1中属于该node节点的特征点索引(每次循环都得到一个)
-
step 2.3 :通过特征点索引idx1在PKF1中取出对应的MapPoint(由于寻找的是未匹配的特征点,所以pMP1应该为NULL)
-
如果pKF1中mvuRight中的值大于0,表示双目,且该特征点有深度,如果是双目相机且没有深度,则退出该点。
-
step 2.4:通过特征点索引idx1在PKF1中取出对应的特征点
-
通过特征点索引idx1在pKF1中取出对应的特征点的描述子
-
step 2.5 遍历该node节点下
(f2it->first)对应KF2中的所有特征点 ,for-
获取PKF2中属于该node节点的特征点索引
-
通过特征点索引idx2在pKF2中取出对应的地图点
-
如果pKF2当前特征点索引idx2已经被匹配过或者对应的3d点非空,那么跳过这个索引idx2
-
如果pKF2中mvuRight中的值大于0,表示双目,且该特征点有深度,如果是双目相机且没有深度,则退出该点。
-
通过特征点索引idx2在pKF2中取出对应的特征点的描述子
-
Step 2.6 计算idx1与idx2在两个关键帧中对应特征点的描述子距离
-
如果距离不符合阈值,则continue
-
通过特征点索引idx2在pKF2中取出对应的特征点kp2
-
为什么双目就不需要判断像素点到极点的距离的判断?
因为双目模式下可以左右互匹配恢复三维点
如果两个点都是单目的,则
- 计算极点坐标与kp2之间的差
- Step 2.7 极点e2到kp2的像素距离如果小于阈值th,认为kp2对应的MapPoint距离pKF1相机太近,跳过该匹配点对
-
Step 2.8 计算特征点kp2到kp1对应极线的距离是否小于阈值,如果符合要求,则更新最佳匹配点及匹配距离
-
-
如果最佳匹配点的索引大于等于0,则
- 记录匹配结果,并标记已经记录的点,避免重复匹配
- 判断是否检查特征点方向,如果检查,则记录旋转差直方图信息
-
-
f1it++;f2it++;
-
-
如果
f1it->first < f2it->first,则f1it = vFeatVec1.lower_bound(f2it->first); -
如果
f1it->first >f2it->first,则f2it = vFeatVec2.lower_bound(f1it->first);
-
-
-
Step 3 用旋转差直方图筛掉错误匹配
-
Step 4 存储匹配关系,下标是关键帧1的特征点id,存储的是关键帧2的特征点id
ORBVocabulary.h
参数:
函数:
PnPSolver.h
参数:
原理:




// 这里的pnp求解用的是EPnP的算法。
// 参考论文:EPnP:An Accurate O(n) Solution to the PnP problem
// https://en.wikipedia.org/wiki/Perspective-n-Point
// http://docs.ros.org/fuerte/api/re_vision/html/classepnp.html
// 如果不理解,可以看看中文的:"摄像机位姿的高精度快速求解" "摄像头位姿的加权线性算法"
// PnP求解:已知世界坐标系下的3D点与图像坐标系对应的2D点,求解相机的外参(R t),即从世界坐标系到相机坐标系的变换。
// 而EPnP的思想是:
// 将世界坐标系所有的3D点用四个虚拟的控制点来表示,将图像上对应的特征点转化为相机坐标系下的四个控制点
// 根据世界坐标系下的四个控制点与相机坐标系下对应的四个控制点(与世界坐标系下四个控制点有相同尺度)即可恢复出(R t)
// |x|
// |u| |fx r u0||r11 r12 r13 t1||y|
// s |v| = |0 fy v0||r21 r22 r23 t2||z|
// |1| |0 0 1 ||r32 r32 r33 t3||1|
// Step 1:用四个控制点来表达所有的3D点
// p_w = sigma(alphas_j * pctrl_w_j), j从0到4
// p_c = sigma(alphas_j * pctrl_c_j), j从0到4
// sigma(alphas_j) = 1, j从0到4
// Step 2:根据针孔投影模型
// s * u = K * sigma(alphas_j * pctrl_c_j), j从0到4
// Step 3:将step2的式子展开, 消去s
// sigma(alphas_j * fx * Xctrl_c_j) + alphas_j * (u0-u)*Zctrl_c_j = 0
// sigma(alphas_j * fy * Xctrl_c_j) + alphas_j * (v0-u)*Zctrl_c_j = 0
// Step 4:将step3中的12未知参数(4个控制点*3维参考点坐标)提成列向量
// Mx = 0,计算得到初始的解x后可以用Gauss-Newton来提纯得到四个相机坐标系的控制点
// Step 5:根据得到的p_w和对应的p_c,用ICP求解出R t
步骤:
-
求所有3D点在世界坐标系下的四个控制点。(我们可以用着四个控制点表示所有的3D点世界坐标系下的坐标,就像A可以由B线性表示一样)
-
根据在世界坐标系下3D点与控制点之间的关系,求解出每个3D点与控制点之间的系数α 。
(我们的目的是根据3D点在相机坐标系和相机坐标系下的坐标,求解出位姿R、t。因为同一个3D点在相机坐标系和相机坐标系的系数α都是一样的,保持不变,所以我们下一步是要找到控制点在相机坐标系的坐标,然后以此求出3D点在相机坐标系下的坐标,在根据ICP求解位姿)

-
求控制点在相机坐标系下的坐标。这一步可以说是本算法的核心,基本上难点都在这一部分。
-
由于我们的输入中包含3D点、3D投影在图像上的2D坐标、相机内参矩阵K,包括焦距和主点。
在这里由于我们不知道深度信息,所以不能直接根据像素点坐标反推出相机坐标系下的坐标。所以我们的想法是将深度信息消去,使用其他的方法替代,如下公式:


-
我们所要做的是计算上述等式Mx=0的解,M是2n x 12的,由2D匹配点和相机内参构成,每个2D点提供两个方程;x是代求的未知量,表示相机坐标系下的控制点坐标。
-
用特征值分解求解上述方程。在这里需要考虑因为焦距不同而导致特征值为0的个数不同的问题,所以要将其分为4中情况求解,零特征值的个数N=4,3,2,1 。
例如当N=4的情况是,假设特征向量为vi,系数为β,x=β1 * v1+β2 * v2+β3 * v3+β4 * v4


-
根据L和ρ,进行SVD求解得到β的值


-
其他的情况也与之类似进行求解,在ORB-SLAM2中,L矩阵都是选定一样的,应该是为了简化计算,根据N的个数,选取对应的方程求解β,
-
使用高斯牛顿的方法对β进行优化

-
其实是对L矩阵求导,然后构建等式方程,求解增量的值



-
使用ICP求解位姿,并返回平均重投影误差

平均重投影误差是根据得到的位姿R、t,将3D投影到像素平面2D点坐标,然后将其与匹配2D点,计算欧氏距离,然后加和后取平均值
-
-
比较平均重投影误差,保存最佳的位姿信息,并返回匹配点对的重投影误差,作为相机位姿估计的评价
函数:
void PnPsolver::choose_control_points(void)
-
@brief 从给定的匹配点中计算出四个控制点
-
首先将参考点的质心(或者称为重心)设置为其中一个控制点,表达如下。这是有一定物理意义的,因为后续会使用质心对坐标点进行归一化
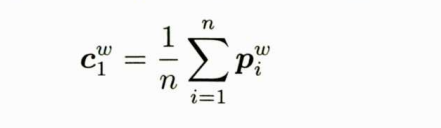
剩下的3个控制点从数据的3个主方向上选取。

步骤
-
Step 1:第一个控制点:参与PnP计算的参考3D点的质心(均值)
- 计算前先把第一个控制点坐标清零
- 遍历每个匹配点中世界坐标系3D点,然后对每个坐标轴加和
- 再对每个轴取均值
-
Step 2:计算其它三个控制点,C1, C2, C3通过特征值分解得到
-
将所有的3D参考点写成矩阵的形式,(number_of_correspondences * 3)的矩阵,首先创建一个nx3的矩阵PW0
-
遍历每个3D点,将其世界坐标减去第一个控制点(均值中心)的坐标(相当于把第一个控制点作为原点),然后将值赋值给创建的nx3的矩阵PW0中
-
计算PW0t * PW0 ,得到3x3协方差矩阵(cvMulTransposed(PW0, &PW0tPW0, 1);)
-
特征值分解
cvSVD(&PW0tPW0, // A &DC, // W,实际是特征值 &UCt, // U,实际是特征向量 0, // V CV_SVD_MODIFY_A | CV_SVD_U_T); // flags -
释放PW0的空间
-
得到C1, C2, C3三个3D控制点,最后加上之前减掉的第一个控制点这个偏移量。(uct每一行对应一个控制点的值,还需要加上之前减掉的第一个控制点这个偏移量)
-
void PnPsolver::compute_barycentric_coordinates(void)
-
@brief 求解世界坐标系下四个控制点的系数alphas,在相机坐标系下系数不变
-
原理



步骤:
-
Step 1:第一个控制点在质心的位置,后面三个控制点减去第一个控制点的坐标(以第一个控制点为原点)
// 减去质心后得到x y z轴 // // cws的排列 |cws1_x cws1_y cws1_z| ---> |cws1| // |cws2_x cws2_y cws2_z| |cws2| // |cws3_x cws3_y cws3_z| |cws3| // |cws4_x cws4_y cws4_z| |cws4| // // cc的排列 |cc2_x cc3_x cc4_x| --->|cc2 cc3 cc4| // |cc2_y cc3_y cc4_y| // |cc2_z cc3_z cc4_z|-
将第一个控制点作为原点,后三个点依次减去第一个控制点,最后得到3x3矩阵,每一行都代表后三个控制点中的一个
-
计算上述矩阵的逆矩阵
-
遍历所有3D点
-
得到pi,pi指向第i个3D点的首地址
-
得到a,a指向第i个控制点系数alphas的首地址
-
根据公式计算

代码中也是在实现上述公式,因为每个3D点对应的控制点系数是不一样的,所以需要有c 步的循环
// pi[]-cws[0][]表示去质心 // a0,a1,a2,a3 对应的是四个控制点的齐次重心坐标 for(int j = 0; j < 3; j++) // +1 是因为跳过了a0 /* 这里的原理基本上是这个样子:(这里公式的下标和程序中的不一样,是从1开始的) * cp=p_i-c1 * cp=a1(c1-c1)+a2(c2-c1)+a3(c3-c1)+a4(c4-c1) * => a2*cc2+a3*cc3+a4*cc4 * [cc2 cc3 cc4] * [a2 a3 a4]^T = cp * => [a2 a3 a4]^T = [cc2 cc3 cc4]^(-1) * cp */ a[1 + j] = ci[3 * j ] * (pi[0] - cws[0][0]) + ci[3 * j + 1] * (pi[1] - cws[0][1]) + ci[3 * j + 2] * (pi[2] - cws[0][2]); // 最后计算用于进行归一化的a0 a[0] = 1.0f - a[1] - a[2] - a[3];
-
-
void PnPsolver::fill_M(CvMat * M, const int row, const double * as, const double u, const double v)
-
@brief 根据提供的每一对点的数据来填充矩阵 M. 每对匹配点的数据可以填充两行,M矩阵在后一步中会用到


-
@param[in] M cvMat对应,存储矩阵M
-
@param[in] row 开始填充数据的行
-
@param[in] as 世界坐标系下3D点用4个虚拟控制点表达时的4个系数
-
@param[in] u 2D点坐标u
-
@param[in] v 2D点坐标v
void PnPsolver::fill_M(CvMat * M,
const int row, const double * as, const double u, const double v)
{
// 第一行起点
double * M1 = M->data.db + row * 12;
// 第二行起点
double * M2 = M1 + 12;
// 对每一个参考点对:
// |ai1*fu, 0, ai1(uc-ui),| ai2*fu, 0, ai2(uc-ui),| ai3*fu, 0, ai3(uc-ui),| ai4*fu, 0, ai4(uc-ui)|
// |0, ai1*fv, ai1(vc-vi),| 0, ai2*fv, ai2(vc-vi),| 0, ai3*fv, ai3(vc-vi),| 0, ai4*fv, ai4(vc-vi)|
// 每一个特征点i有两行,每一行根据j=1,2,3,4可以分成四个部分,这也就是下面的for循环中所进行的工作
for(int i = 0; i < 4; i++) {
M1[3 * i ] = as[i] * fu;
M1[3 * i + 1] = 0.0;
M1[3 * i + 2] = as[i] * (uc - u);
M2[3 * i ] = 0.0;
M2[3 * i + 1] = as[i] * fv;
M2[3 * i + 2] = as[i] * (vc - v);
}
}
void PnPsolver::compute_pcs(void)
- @brief 根据相机坐标系下控制点坐标ccs 和控制点系数 alphas(通过世界坐标系下3D点计算得到),得到相机坐标系下3D点坐标 pcs
- 过程可以参考 https://blog.csdn.net/jessecw79/article/details/82945918
void PnPsolver::compute_pcs(void)
{
// 遍历所有的空间点
for(int i = 0; i < number_of_correspondences; i++) {
// 定位
double * a = alphas + 4 * i;
double * pc = pcs + 3 * i;
// 计算
for(int j = 0; j < 3; j++)
pc[j] = a[0] * ccs[0][j] + a[1] * ccs[1][j] + a[2] * ccs[2][j] + a[3] * ccs[3][j];
}
}
void PnPsolver::compute_L_6x10(const double * ut, double * l_6x10)
-
@brief 计算矩阵L,论文式13中的L矩阵,不过这里的是按照N=4的时候计算的,
-
@param[in] ut 特征值分解之后得到的12x12特征矩阵
-
@param[out] l_6x10 计算的L矩阵结果,维度6x10
-
v1、2、3、4均为12x1的特征向量,例如v1可拆分为4个3x1的相邻,单独看v1就有6个不同的组合

我们要保证每次方程或者说L矩阵每一行都是同一个组合
-


步骤:
-
Step 1 获取最后4个零特征值对应的4个12x1的特征向量
-
因为这里对应的是EPNP中N=4的情况,所以直接去特征向量的最后4行
-
// 以这里的v[0]为例,它是12x1的向量,会拆成4个3x1的向量v[0]^[0],v[0]^[1],v[0]^[1],v[0]^[3],对应4个相机坐标系控制点 v[0] = ut + 12 * 11; // v[0] : v[0][0]~v[0][2] => v[0]^[0] , * \beta_0 = c0 (理论上) // v[0][3]~v[0][5] => v[0]^[1] , * \beta_0 = c1 // v[0][6]~v[0][8] => v[0]^[2] , * \beta_0 = c2 // v[0][9]~v[0][11] => v[0]^[3] , * \beta_0 = c3
-
-
Step 2提前计算中间变量dv
-
dv表示中间向量,是difference-vector的缩写
// 4 表示N=4时对应的4个12x1的向量v, 6 表示4对点一共有6种两两组合的方式,3 表示v^[i]是一个3维的列向量 double dv[4][6][3]; -
开始循环,构建每一种情况。 N=4时候的情况. 控制第一个下标的就是a,第二个下标的就是b,不过下面的循环中下标都是从0开始的。
for(int i = 0; i < 4; i++) { // 每一个向量v[i]可以提供四个控制点的"雏形"v[i]^[0]~v[i]^[3] // 这四个"雏形"两两组合一共有六种组合方式: // 下面的a变量就是前面的那个id,b就是后面的那个id int a = 0, b = 1; for(int j = 0; j < 6; j++) { // dv[i][j]=v[i]^[a]-v[i]^[b] // a,b的取值有6种组合 0-1 0-2 0-3 1-2 1-3 2-3 dv[i][j][0] = v[i][3 * a ] - v[i][3 * b ]; dv[i][j][1] = v[i][3 * a + 1] - v[i][3 * b + 1]; dv[i][j][2] = v[i][3 * a + 2] - v[i][3 * b + 2]; b++; if (b > 3) { a++; b = a + 1; } } }
-
-
Step 3 用前面计算的dv生成L矩阵
// 这里的6代表前面每个12x1维向量v的4个3x1子向量v^[i]对应的6种组合 for(int i = 0; i < 6; i++) { double * row = l_6x10 + 10 * i; // 计算每一行中的每一个元素,总共是10个元素 // 对应的\beta列向量 row[0] = dot(dv[0][i], dv[0][i]); //*b11 row[1] = 2.0f * dot(dv[0][i], dv[1][i]); //*b12 row[2] = dot(dv[1][i], dv[1][i]); //*b22 row[3] = 2.0f * dot(dv[0][i], dv[2][i]); //*b13 row[4] = 2.0f * dot(dv[1][i], dv[2][i]); //*b23 row[5] = dot(dv[2][i], dv[2][i]); //*b33 row[6] = 2.0f * dot(dv[0][i], dv[3][i]); //*b14 row[7] = 2.0f * dot(dv[1][i], dv[3][i]); //*b24 row[8] = 2.0f * dot(dv[2][i], dv[3][i]); //*b34 row[9] = dot(dv[3][i], dv[3][i]); //*b44 }
void PnPsolver::compute_rho(double * rho)
-
@brief 计算四个控制点任意两点间的距离,总共6个距离,对应论文式13中的向量\rho
-
@param[in] rho 计算结果
-
该步对应的是ρ 6x1

void PnPsolver::compute_rho(double * rho)
{
// 四个点两两组合一共有6中组合方式: 01 02 03 12 13 23
rho[0] = dist2(cws[0], cws[1]);
rho[1] = dist2(cws[0], cws[2]);
rho[2] = dist2(cws[0], cws[3]);
rho[3] = dist2(cws[1], cws[2]);
rho[4] = dist2(cws[1], cws[3]);
rho[5] = dist2(cws[2], cws[3]);
}
void PnPsolver::find_betas_approx_1(const CvMat * L_6x10, const CvMat * Rho, double * betas)
-
@brief 计算N=4时候的粗糙近似解,暴力将其他量置为0
-
@param[in] L_6x10 矩阵L
-
@param[in] Rho 非齐次项 \rho, 列向量
-
@param[out] betas 计算得到的beta


因为我们需要得到的β是1、2、3、4,而β10x1 都是由β1 、2、3、4构成的,所以简化计算,可以挑选4个变量,包含β1、2、3、4这四个值,然后计算即可
步骤:
-
// 计算N=4时候的粗糙近似解,暴力将其他量置为0 // betas10 = [B11 B12 B22 B13 B23 B33 B14 B24 B34 B44] -- L_6x10中每一行的内容 // betas_approx_1 = [B11 B12 B13 B14 ] -- L_6x4 中一行提取出来的内容 -
提取L_6x10矩阵中每行的第0,1,3,6个元素,得到L_6x4
-
SVD方式求解方程组 L_6x4 * B4 = Rho
cvSolve(&L_6x4, Rho, &B4, CV_SVD); -
根据B4和公式11-39,求解β1、2、3、4
void PnPsolver::find_betas_approx_2(const CvMat * L_6x10, const CvMat * Rho, double * betas)
-
@brief 计算N=2时候的粗糙近似解,暴力将其他量置为0
-
@param[in] L_6x10 矩阵L
-
@param[in] Rho 非齐次项 \rho, 列向量
-
@param[out] betas 计算得到的beta
-
这里与N=4的情况一样,不过由于N=2是只有β1、2,所以只需要保留这两个量即可

void PnPsolver::find_betas_approx_2(const CvMat * L_6x10, const CvMat * Rho,
double * betas)
{
// betas10 = [B11 B12 B22 B13 B23 B33 B14 B24 B34 B44]
// betas_approx_2 = [B11 B12 B22 ]
double l_6x3[6 * 3], b3[3];
CvMat L_6x3 = cvMat(6, 3, CV_64F, l_6x3);
CvMat B3 = cvMat(3, 1, CV_64F, b3);
// 提取
for(int i = 0; i < 6; i++) {
cvmSet(&L_6x3, i, 0, cvmGet(L_6x10, i, 0));
cvmSet(&L_6x3, i, 1, cvmGet(L_6x10, i, 1));
cvmSet(&L_6x3, i, 2, cvmGet(L_6x10, i, 2));
}
// 求解方程组
cvSolve(&L_6x3, Rho, &B3, CV_SVD);
// 从b11 b12 b22 中恢复 b1 b2
if (b3[0] < 0) {
betas[0] = sqrt(-b3[0]);
betas[1] = (b3[2] < 0) ? sqrt(-b3[2]) : 0.0;
} else {
betas[0] = sqrt(b3[0]);
betas[1] = (b3[2] > 0) ? sqrt(b3[2]) : 0.0;
}
void PnPsolver::find_betas_approx_3(const CvMat * L_6x10, const CvMat * Rho, double * betas)
-
@brief 计算N=3时候的粗糙近似解,暴力将其他量置为0
-
@param[in] L_6x10 矩阵L
-
@param[in] Rho 非齐次项 \rho, 列向量
-
@param[out] betas 计算得到的beta
-
N=3有三个变量需要求,β1、2、3,挑选出包含这三个对应的数据

void PnPsolver::find_betas_approx_3(const CvMat * L_6x10, const CvMat * Rho,
double * betas)
{
// betas10 = [B11 B12 B22 B13 B23 B33 B14 B24 B34 B44]
// betas_approx_3 = [B11 B12 B22 B13 B23 ]
double l_6x5[6 * 5], b5[5];
CvMat L_6x5 = cvMat(6, 5, CV_64F, l_6x5);
CvMat B5 = cvMat(5, 1, CV_64F, b5);
// 获取并构造矩阵
for(int i = 0; i < 6; i++) {
cvmSet(&L_6x5, i, 0, cvmGet(L_6x10, i, 0));
cvmSet(&L_6x5, i, 1, cvmGet(L_6x10, i, 1));
cvmSet(&L_6x5, i, 2, cvmGet(L_6x10, i, 2));
cvmSet(&L_6x5, i, 3, cvmGet(L_6x10, i, 3));
cvmSet(&L_6x5, i, 4, cvmGet(L_6x10, i, 4));
}
// 求解这个方程组
cvSolve(&L_6x5, Rho, &B5, CV_SVD);
// 从 B11 B12 B22 B13 B23 中恢复出 B1 B2 B3
if (b5[0] < 0) {
betas[0] = sqrt(-b5[0]);
betas[1] = (b5[2] < 0) ? sqrt(-b5[2]) : 0.0;
} else {
betas[0] = sqrt(b5[0]);
betas[1] = (b5[2] > 0) ? sqrt(b5[2]) : 0.0;
}
if (b5[1] < 0) betas[0] = -betas[0];
betas[2] = b5[3] / betas[0];
// N=3的时候没有B4
betas[3] = 0.0;
}
void PnPsolver::compute_A_and_b_gauss_newton(const double * l_6x10, const double * rho, double betas[4], CvMat * A, CvMat * b)
-
@brief 计算高斯牛顿法优化时,增量方程中的系数矩阵和非齐次项
-
@param[in] l_6x10 L矩阵
-
@param[in] rho Rho矩向量
-
@param[in] cb 当前次迭代得到的beta1~beta4
-
@param[out] A 计算得到的增量方程中的系数矩阵
-
@param[out] b 计算得到的增量方程中的非齐次项



步骤:
-
一共有6个方程组,对每一行(也就是每一个方程展开遍历)。从优化目标函数的概念出发,其中的每一行的约束均由一对点来提供,因此不同行之间其实并无关系,可以相互独立地计算。 for
-
根据公式计算当前行的雅克比

-
计算当前行的非齐次项

ρ前面已得到,Lβ的计算如下

-
void PnPsolver::qr_solve(CvMat * A, CvMat * b, CvMat * X)
- @brief 使用QR分解来求解增量方程
- @param[in] A 系数矩阵
- @param[in] b 非齐次项
- @param[out] X 增量
【速成】矩阵论Givens变换QR分解_哔哩哔哩_bilibili
void PnPsolver::gauss_newton(const CvMat * L_6x10, const CvMat * Rho, double betas[4])
- @brief 对计算出来的Beta结果进行高斯牛顿法优化,求精. 过程参考EPnP论文中式(15)
- @param[in] L_6x10
- @param[in] Rho
- @param[in] betas
这里是求解增量方程组Ax=B,其中的x就是增量. 根据论文中的式15,可以得到优化的目标函数为:
$ f(\mathbf{\beta})=\sum_{(i,j \ s.t. \ i<j)} \left( ||\mathbf{c}c_i-\mathbf{c}c_j ||^2 - ||\mathbf{c}w_i-\mathbf{c}w_j ||^2 \right) $
而根据高斯牛顿法,增量方程为:
$ \mathbf{H}\mathbf{\Delta x}=\mathbf{g} $
也就是:(参考视觉SLAM十四讲第一版P112式6.21 6.22)
$ \mathbf{J}^T\mathbf{J}\mathbf{\Delta x}=-\mathbf{J}^T f(x) $
不过这里在计算的时候将等式左右两边的雅克比$ \mathbf{J}^T $都给约去了,得到精简后的增量方程:
$ \mathbf{J}\mathbf{\Delta x}=-f(x) $
然后分别对应为程序代码中的系数矩阵A和非齐次项B.



步骤:
-
设置迭代次数,这里设置的是5次
-
初始化参数 A (6x4)、B (6x1) 、 X (4x1)
-
对于每次迭代过程 for
-
计算增量方程的系数矩阵和非齐次项
compute_A_and_b_gauss_newton(L_6x10->data.db, Rho->data.db, betas, &A, &B); -
使用QR分解来求解增量方程,解的当前次迭代的增量X
qr_solve(&A, &B, &X); -
应用增量,对估计值进行更新,估计值是beta1~beta4组成的向量
for(int i = 0; i < 4; i++) betas[i] += x[i];
-
void PnPsolver::estimate_R_and_t(double R[3][3], double t[3])
- @brief 用3D点在世界坐标系和相机坐标系下对应的坐标,用ICP求取R t
- @param[out] R 旋转
- @param[out] t 平移

void PnPsolver::compute_ccs(const double * betas, const double * ut)
-
@brief 通过给出的beta和vi,计算控制点在相机坐标系下的坐标
-
@param[in] betas beta
-
@param[in] ut 其实是vi,
即在求解等式
 时
时M经过奇异值分解后得到的特征值对应的特征向量的集合,ut为原特征向量的转置,因为我们选取的是特征值为0 的情况,所以应选择最后几行,为其基础解系

void PnPsolver::compute_ccs(const double * betas, const double * ut)
{
// Step 1 清空4个控制点坐标ccs
for(int i = 0; i < 4; i++)
ccs[i][0] = ccs[i][1] = ccs[i][2] = 0.0f;
// Step 2 根据前面计算的beta和v计算控制点坐标
for(int i = 0; i < 4; i++) {
// 注意这里传过来的向量ut中,最后的部分才是v,依次是 x x x ... x v4 v3 v2 v1
// 这里就是在最后面一次取出 v1 ~ v4
const double * v = ut + 12 * (11 - i);
for(int j = 0; j < 4; j++) // j表示当前计算的是第几个控制点
for(int k = 0; k < 3; k++) // k表示当前计算的是控制点的哪个坐标
ccs[j][k] += betas[i] * v[3 * j + k];
}
}
void PnPsolver::compute_pcs(void)
-
@brief 根据相机坐标系下控制点坐标ccs 和控制点系数 alphas(通过世界坐标系下3D点计算得到),得到相机坐标系下3D点坐标 pcs
-
过程可以参考 https://blog.csdn.net/jessecw79/article/details/82945918
-

void PnPsolver::compute_pcs(void)
{
// 遍历所有的空间点
for(int i = 0; i < number_of_correspondences; i++) {
// 定位
double * a = alphas + 4 * i;
double * pc = pcs + 3 * i;
// 计算
for(int j = 0; j < 3; j++)
pc[j] = a[0] * ccs[0][j] + a[1] * ccs[1][j] + a[2] * ccs[2][j] + a[3] * ccs[3][j];
}
}
void PnPsolver::solve_for_sign(void)
保持所有点在相机坐标系下的深度为正,调整符号。主要是根据第一个点的深度,来对其余点进行更新。
void PnPsolver::solve_for_sign(void)
{
// 根据第一个3D点在当前相机坐标系下的深度,调整所有的3D点的深度为正(因为正常地来讲,这些3D点都应该是在相机前面的)
// 如果第一个点的深度是负的话
if (pcs[2] < 0.0) {
// 先调整控制点的坐标
for(int i = 0; i < 4; i++)
for(int j = 0; j < 3; j++)
ccs[i][j] = -ccs[i][j];
// 然后调整3D点的坐标
for(int i = 0; i < number_of_correspondences; i++) {
pcs[3 * i ] = -pcs[3 * i];
pcs[3 * i + 1] = -pcs[3 * i + 1];
pcs[3 * i + 2] = -pcs[3 * i + 2];
}
}
}
double PnPsolver::reprojection_error(const double R[3][3], const double t[3])
- @brief 计算在给定位姿的时候的3D点投影误差
- @param[in] R 给定旋转
- @param[in] t 给定平移
- @return double 重投影误差,是平均到每一对匹配点上的误差
步骤:
- 遍历每个3D点 ,例一个点
- 获取该3D点坐标
- 计算该3D点在相机坐标系下的坐标,逆深度表示
- 计算投影点坐标
- 获取匹配2D点的坐标(已知)
- 计算投影点与匹配2D单的欧氏距离的平方
- 得到其欧氏距离并累加
- 返回平均误差
sum2 / number_of_correspondences
double PnPsolver::compute_R_and_t(const double * ut, const double * betas, double R[3][3], double t[3])
- @brief 根据已经得到的控制点在当前相机坐标系下的坐标来恢复出相机的位姿
- @param[in] ut vi
- @param[in] betas betas
- @param[out] R 计算得到的相机旋转R
- @param[out] t 计算得到的相机位置t
- @return double 使用这个位姿,所得到的重投影误差
步骤:
-
根据前面的计算结果来“组装”得到控制点在当前相机坐标系下的坐标
compute_ccs(betas, ut); -
将世界坐标系下的3D点的坐标转换到控制点的坐标系下 (根据相机坐标系下控制点坐标ccs 和控制点系数 alphas(通过世界坐标系下3D点计算得到),得到相机坐标系下3D点坐标 pcs)
compute_pcs(); -
调整坐标的符号,来保证相机坐标系下点的深度为正
solve_for_sign(); -
ICP计算R和t
estimate_R_and_t(R, t); -
计算使用这个位姿,所得到的每对点平均的重投影误差,作为返回值
return reprojection_error(R, t);
double PnPsolver::compute_pose(double R[3][3], double t[3])
- @brief 使用EPnP算法计算相机的位姿.其中匹配点的信息由类的成员函数给定
- @param[out] R 求解位姿里的旋转矩阵
- @param[out] T 求解位姿里的平移向量
- @return double 使用这对旋转和平移的时候, 匹配点对的平均重投影误差

步骤:
-
获得EPNP算法中的四个控制点
choose_control_points(); -
计算世界坐标系下每个3D点用4个控制点线性表达时的系数alphas
compute_barycentric_coordinates(); -
构造M矩阵,EPnP原始论文中公式(3)(4)–>(5)(6)(7); 矩阵的大小为 2n*12 ,n 为使用的匹配点的对数
fill_M(M, 2 * i, alphas + 4 * i, us[2 * i], us[2 * i + 1]); -
求解Mx=0
-
Step 4.1 先计算其中的特征向量vi
- 求协方差矩阵 MtM (12 x 12) ( M 是2n x 12 )
cvMulTransposed(M, &MtM, 1); - 对MtM进行特征值分解
cvSVD(&MtM, &D, &Ut, 0, CV_SVD_MODIFY_A | CV_SVD_U_T);
- 求协方差矩阵 MtM (12 x 12) ( M 是2n x 12 )
-
Step 4.2计算分情况讨论的时候需要用到的矩阵L(6x10)和ρ(6x1),在这里是按照N=4计算的
compute_L_6x10(ut, l_6x10); compute_rho(rho); -
Step 4.3分情况计算N=2,3,4时,能够求解得到的相机位姿R,t,并且得到平均重投影误差
(不管什么情况,都假设论文中N=4,并求解部分betas(如果全求解出来会有冲突),通过优化得到剩下的 betas,最后计算R t)
-
求解近似解:N=4的情况
-
根据L和ρ,计算β
find_betas_approx_1(&L_6x10, &Rho, Betas[1]); -
利用高斯牛顿法迭代优化得到β
gauss_newton(&L_6x10, &Rho, Betas[1]); -
计算相机的位姿(R 、t),并得到平均重投影误差
rep_errors[1] = compute_R_and_t(ut, Betas[1], Rs[1], ts[1]);
-
-
求解近似解:N=2的情况
-
根据L和ρ,计算β
find_betas_approx_2(&L_6x10, &Rho, Betas[2]); -
利用高斯牛顿法迭代优化得到β
gauss_newton(&L_6x10, &Rho, Betas[2]); -
计算相机的位姿(R 、t),并得到平均重投影误差
rep_errors[2] = compute_R_and_t(ut, Betas[2], Rs[2], ts[2]);
-
-
求解近似解:N=3的情况
-
根据L和ρ,计算β
find_betas_approx_3(&L_6x10, &Rho, Betas[3]); -
利用高斯牛顿法迭代优化得到β
gauss_newton(&L_6x10, &Rho, Betas[3]); -
计算相机的位姿(R 、t),并得到平均重投影误差
rep_errors[3] = compute_R_and_t(ut, Betas[3], Rs[3], ts[3]);
-
-
-
-
看看哪种情况得到的效果最好,然后就选哪个
int N = 1; // trick , 这样可以减少一种情况的计算 if (rep_errors[2] < rep_errors[1]) N = 2; if (rep_errors[3] < rep_errors[N]) N = 3; -
将最佳计算结果保存到返回计算结果用的变量中
-
并且返回平均匹配点对的重投影误差,作为对相机位姿估计的评价
Sim3Solver.h
参数:
原理:













函数:
void Sim3Solver::ComputeCentroid(cv::Mat &P, cv::Mat &Pr, cv::Mat &C)
- @brief 给出三个点,计算它们的质心以及去质心之后的坐标
- @param[in] P 输入的3D点
- @param[in] Pr 去质心后的点
- @param[in] C 质心
void Sim3Solver::ComputeCentroid(cv::Mat &P, cv::Mat &Pr, cv::Mat &C)
{
// 矩阵P每一行求和,结果存在C。这两句也可以使用CV_REDUCE_AVG选项来实现
cv::reduce(P,C,1,CV_REDUCE_SUM);
C = C/P.cols;// 求平均
for(int i=0; i<P.cols; i++)
{
Pr.col(i)=P.col(i)-C;//减去质心
}
}
void Sim3Solver::ComputeSim3(cv::Mat &P1, cv::Mat &P2)
- @brief 根据两组匹配的3D点,计算P2到P1的Sim3变换
- @param[in] P1 匹配的3D点(三个,每个的坐标都是列向量形式,三个点组成了3x3的矩阵)(当前关键帧)
- @param[in] P2 匹配的3D点(闭环关键帧)
- Sim3计算过程参考论文:Horn 1987, Closed-form solution of absolute orientataion using unit quaternions
步骤:
-
step 1 定义3D点质心及去质心后的点
-
O1和O2 分别为P1 和P2 矩阵中3D点的质心
-
Pr1和Pr2 为减去质心后的3D点
-
ComputeCentroid(P1,Pr1,O1); ComputeCentroid(P2,Pr2,O2);
-
-
step 2 计算论文中三维点数目 n>3 的M矩阵。这里只使用了3个点。
Pr2 对应论文中 r_l,i’,Pr1 对应论文中 r_r,i’,计算的是P2到P1的Sim3,论文中是left 到 right的Sim3
cv::Mat M = Pr2*Pr1.t(); -
计算论文中的N矩阵,根据

-
Step 4: 特征值分解求最大特征值对应的特征向量,就是我们要求的旋转四元数
-
使用
cv::eigen(N,eval,evec)进行特征值分解,特征值默认是从大到小排列,所以evec[0] 是最大值 -
N 矩阵最大特征值(第一个特征值)对应特征向量就是要求的四元数(q0 q1 q2 q3),其中q0 是实部。将(q1 q2 q3)放入vec(四元数的虚部)
-
四元数虚部模长 norm(vec)=sin(theta/2), 四元数实部 evec.at(0,0)=q0=cos(theta/2)。
这一步的ang实际是theta/2,theta 是旋转向量中旋转角度
vec/norm(vec)归一化得到归一化后的旋转向量,然后乘上角度得到包含了旋转轴和旋转角信息的旋转向量vec
将 旋转向量(轴角)转换为旋转矩阵
-
-
step 5 利用刚计算出来的旋转将三维点旋转到同一个坐标系,P3对应论文里的 r_l,i’, Pr1 对应论文里的r_r,i
’
cv::Mat P3 = mR12i*Pr2; -
step 6 计算尺度因子 scale
-
判断当前传感器下是否需要计算尺度因子
-
根据公式计算尺度因子

-
-
step 7 计算平移Translation

-
step 8 计算双向变换矩阵,目的是在后面的检查的过程中能够进行双向的投影操作
-
step 8.1 用尺度,旋转,平移构建变换矩阵 T12
mT12i = cv::Mat::eye(4,4,P1.type()); cv::Mat sR = ms12i*mR12i; // |sR t| // mT12i = | 0 1| sR.copyTo(mT12i.rowRange(0,3).colRange(0,3)); mt12i.copyTo(mT12i.rowRange(0,3).col(3)); -
step 8.2 计算变换矩阵T21
mT21i = cv::Mat::eye(4,4,P1.type()); cv::Mat sRinv = (1.0/ms12i)*mR12i.t(); sRinv.copyTo(mT21i.rowRange(0,3).colRange(0,3)); cv::Mat tinv = -sRinv*mt12i; tinv.copyTo(mT21i.rowRange(0,3).col(3));
-
void Sim3Solver::FromCameraToImage(const vector< cv::Mat> &vP3Dc, vector< cv::Mat> &vP2D, cv::Mat K)
- @brief 计算当前关键帧中的地图点在当前关键帧图像上的投影坐标
- @param[in] vP3Dc 相机坐标系下三维点坐标
- @param[in] vP2D 投影的二维图像坐标
- @param[in] K 内参矩阵
步骤:
- 获取相机内参
- 遍历当前关键帧中的所有地图点(这里对应的是相机坐标系下的三维点坐标),根据内参,将其转换为图像上的投影坐标
void Sim3Solver::Project(const vector< cv::Mat> &vP3Dw, vector< cv::Mat> &vP2D, cv::Mat Tcw, cv::Mat K)
- @brief 按照给定的Sim3变换进行投影操作,得到三维点的2D投影点
- @param[in] vP3Dw 3D点
- @param[in & out] vP2D 投影到图像的2D点
- @param[in] Tcw Sim3变换
- @param[in] K 内参
步骤:
- 获取经过sim3得到的旋转R和平移t
- 获取相机内参
- 对每个3D地图点(世界坐标系下的地图点)进行投影操作,for
- 首先将对方关键帧的地图点坐标转换到这个关键帧的相机坐标系下(经过旋转、平移)
- 将相机坐标系下的坐标投影到二维图像上(经过相机内参)
- 保存投影后的二维坐标
void Sim3Solver::SetRansacParameters(double probability, int minInliers, int maxIterations)
- @brief 设置进行RANSAC时的参数
- @param[in] probability 当前这些匹配点的置信度,也就是一次采样恰好都是内点的概率
- @param[in] minInliers 完成RANSAC所需要的最少内点个数
- @param[in] maxIterations 设定的最大迭代次数

void Sim3Solver::SetRansacParameters(double probability, int minInliers, int maxIterations)
{
mRansacProb = probability; // 0.99
mRansacMinInliers = minInliers; // 20
mRansacMaxIts = maxIterations; // 最大迭代次数 300
// 匹配点的数目
N = mvpMapPoints1.size(); // number of correspondences
// 内点标记向量
mvbInliersi.resize(N);
// Adjust Parameters according to number of correspondences
float epsilon = (float)mRansacMinInliers/N;
// Set RANSAC iterations according to probability, epsilon, and max iterations
// 计算迭代次数的理论值,也就是经过这么多次采样,其中至少有一次采样中,三对点都是内点
// epsilon 表示了在这 N 对匹配点中,我随便抽取一对点是内点的概率;
// 为了计算Sim3,我们需要从这N对匹配点中取三对点;那么如果我有放回的从这些点中抽取三对点,取这三对点均为内点的概率是 p0=epsilon^3
// 相应地,如果取三对点中至少存在一对匹配点是外点, 概率为p1=1-p0
// 当我们进行K次采样的时候,其中每一次采样中三对点中都存在至少一对外点的概率就是p2=p1^k
// K次采样中,至少有一次采样中三对点都是内点的概率是p=1-p2
// 候根据 p2=p1^K 我们就可以导出 K 的公式:K=\frac{\log p2}{\log p1}=\frac{\log(1-p)}{\log(1-epsilon^3)}
// 也就是说,我们进行K次采样,其中至少有一次采样中,三对点都是内点; 因此我们就得到了RANSAC迭代次数的理论值
int nIterations;
if(mRansacMinInliers==N)
nIterations=1; // 这种情况的时候最后计算得到的迭代次数的确就是一次
else
nIterations = ceil(log(1-mRansacProb)/log(1-pow(epsilon,3)));
// 外层的max保证RANSAC能够最少迭代一次;
// 内层的min的目的是,如果理论值比给定值要小,那么我们优先选择使用较少的理论值来节省时间(其实也有极大概率得到能够达到的最好结果);
// 如果理论值比给定值要大,那么我们也还是有限选择使用较少的给定值来节省时间
mRansacMaxIts = max(1,min(nIterations,mRansacMaxIts));
// 当前正在进行的迭代次数
mnIterations = 0;
}
void Sim3Solver::CheckInliers()
- @brief 通过计算的Sim3投影,和自身投影的误差比较,进行内点检测
步骤:
-
分别将各自的3D点经过Sim3变换到另一系中,计算重投影坐标
// 用计算的Sim3 对所有的地图点投影,得到图像点 vector<cv::Mat> vP1im2, vP2im1; Project(mvX3Dc2,vP2im1,mT12i,mK1);// 把2系中的3D经过Sim3变换(mT12i)到1系中计算重投影坐标 Project(mvX3Dc1,vP1im2,mT21i,mK2);// 把1系中的3D经过Sim3变换(mT21i)到2系中计算重投影坐标 -
对于两帧的每一个匹配点,for
-
当前关键帧中的地图点直接在当前关键帧图像上的投影坐标mvP1im1,mvP2im2
对于这对匹配关系,在两帧上的投影点距离都要进行计算
cv::Mat dist1 = mvP1im1[i]-vP2im1[i]; cv::Mat dist2 = vP1im2[i]-mvP2im2[i]; -
取距离的平方作为误差
-
根据之前确定的这个最大容许误差来确定这对匹配点是否是外点,并标记内外点,统计内点的个数
-
cv::Mat Sim3Solver::iterate(int nIterations, bool &bNoMore, vector< bool> &vbInliers, int &nInliers)
- @brief Ransac求解mvX3Dc1和mvX3Dc2之间Sim3,函数返回mvX3Dc2到mvX3Dc1的Sim3变换
- @param[in] nIterations 设置的最大迭代次数
- @param[in] bNoMore 为true表示穷尽迭代还没有找到好的结果,说明求解失败
- @param[in] vbInliers 标记是否是内点
- @param[in] nInliers 内点数目
- @return cv::Mat 计算得到的Sim3矩阵
步骤:
-
step 1 如果匹配点比要求的最少内点数还少,则不满足Sim3 求解条件,返回空
-
step 2 随机选择三个点,用于求解后面的Sim3
-
条件1 已经进行的总迭代次数还没有超过限制的最大总迭代次数
-
条件2 当前迭代次数还没有超过理论迭代次数
-
开始进入循环
while(mnIterations<mRansacMaxIts && nCurrentIterations<nIterations)-
更新迭代次数
-
记录所有有效(可以采样)的候选三维点索引
-
step 2.1 随机取三组点,取完后从候选索引中删掉,for
-
使用DBoW3中的随机数生成函数得到一个整数
-
获取点对的索引
-
//根据点的存储方式获取点对坐标 // P3Dc1i和P3Dc2i中点的排列顺序: // x1 x2 x3 ... // y1 y2 y3 ... // z1 z2 z3 ... -
从"可用索引列表"中删除这个点的索引
-
-
Step 2.2 根据随机取的两组匹配的3D点,计算P3Dc2i 到 P3Dc1i 的Sim3变换
ComputeSim3(P3Dc1i,P3Dc2i); -
Step 2.3 对计算的Sim3变换,通过投影误差进行inlier检测
CheckInliers(); -
Step 2.4 记录并更新最多的内点数目及对应的参数
- 如果检测到的内点数大于最好一次迭代中得到的内点个数,则
- 记录并更新最多的内点数及对应的参数
- 如果检测到的内点数大于RANSAC的理想条件的最少内点数,就算是计算得到一次合格的Sim变换,则记录内点数目,标记已经确定的内点,返回最好的变换矩阵
- 如果检测到的内点数大于最好一次迭代中得到的内点个数,则
-
-
-
step 3 如果已经达到了最大迭代次数了还没得到满足条件的Sim3,说明失败了,放弃,返回空矩阵
System.h
参数:
函数:
Tracking.h
参数:
原理:
跟踪线程的整个流程

参考关键帧原理
参考关键帧跟踪就是将当前普通帧(位姿未知)和它对应的参考关键帧(已知)进行特征匹配及优化,从而估计当前普通帧的位姿。
-
参考关键帧跟踪的应用场景如下。
(1)情况1。地图刚刚初始化之后,此时恒速模型中的速度为空。这时只能使用参考关键帧,也就是初始化的第1、2帧对当前帧进行跟踪。
( 2)情况2。恒速模型跟踪失败后,尝试用最近的参考关键帧跟踪当前普通帧。因为在恒速模型中估计的速度并不准确,可能会导致错误匹配,并且恒速模型只利用了前一帧的信息,信息量也有限,跟踪失败的可能性较大。而参考关键帧可能在局部建图线程中新匹配了更多的地图点,并且参考关键帧的位姿是经过多次优化的,更准确。 -
具体流程
第1步,将当前普通帧的描述子转化为词袋向量。
第2步,通过词袋加快当前普通帧和参考关键帧之间的特征点匹配。使用前面讲过的特征匹配函数SearchByBoW(),之所以能够加速,是因为它只对属于同一节点的特征点进行匹配,大大缩小了匹配范围,提高了匹配成功率。记录特征匹配成功后当前帧每个特征点对应的地图点(来自参考关键帧),用于后续进一步的3D-2D投影优化位姿。
第3步,将上一帧的位姿作为当前帧位姿的初始值(可以加速收敛),通过优化3D-2D的重投影误差获得准确位姿。三维地图点来自第2步匹配成功的参考帧,二维特征点来自当前普通帧,BA优化仅优化位姿,不优化地图点坐标。优化函数具体见第14章内容。
第4步,剔除优化后的匹配点中的外点。
如果最终成功匹配的地图点数目超过阈值,则认为成功跟踪,否则认为跟踪失败。

恒速模型跟踪
什么是恒速模型跟踪?
因为两个图像帧之间一般只有几十毫秒的时间,这么短的时间,可以合理的假设——在相邻帧间极短的时间内,相机处于匀速运动状态,可以用上一帧的位姿和速度估计当前帧的位姿。所以称为恒速模型跟踪。
有了参考关键帧跟踪,为什么还要用恒速模型跟踪呢?
地图刚刚初始化后,用参考关键帧跟踪是因为“被逼无奈”,此时没有速度信息,只能用词袋匹配估计一个粗糙的位姿,再非线性优化该位姿。使用参考关键帧跟踪成功后,就有了速度信息,此时我们就不需要再用比较复杂的参考关键帧跟踪了,直接用恒速模型跟踪估计位姿更简单、更快,这对实时性要求较高的SLAM 系统来说很有意义。
恒速模型的位姿更新过程
如下图示为恒速模型的位姿更新过程(该部分是恒速模型跟踪和参考关键帧跟踪的主要区别之一)。可以分为以下几步:
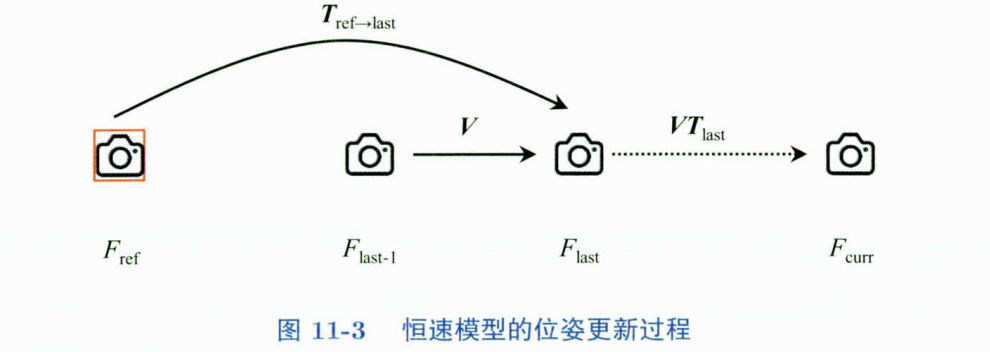
以上更新位姿时针对单目相机,双目和RGB-D相机的过程不同:
- 第1步,利用参考关键帧更新上一帧在世界坐标系下的位姿。
- 第2步,对于双目相机或RGB-D相机,为上一帧生成新的临时地图点。具体来说,就是把上一帧中有深度值但还没被标记为地图点的三维点作为临时地图点,这些临时地图点只是为了提高跟踪的稳定性,在创建时并没有添加到全局地图中,并且标记为临时添加属性(在跟踪结束后会删除)。当深度值较大或者地图点数目足够时,停止添加。
恒速模型跟踪流程
- 更新上一帧的位姿,对于双目相机和RGB-D相机来说,还会根据深度值生成临时地图点
- 根据之前估计的速度(速度在Track( )构造函数中就获得了),用很俗模型得到当前帧的初始位姿
- 用上一帧的地图点进行投影匹配,如果匹配点不够,则扩大搜索半径再试一次
- 利用3D-2D投影关系,优化当前帧的位姿
- 剔除匹配成功的特征点对数目,若超过阈值,则认为跟踪成功
恒速模型跟踪的优缺点
- 优点1。跟踪仅需要上一帧的信息,是跟踪第一阶段中最常使用的跟踪方法。
- 优点2。增加了一些技巧,可提高跟踪的稳定性。比如,在双目相机和RGB-D相机模式下生成的临时地图点可提高跟踪的成功率;投影匹配数目不足时没有马上放弃,而是将搜索范围扩大一倍再试一次。
- 缺点。恒速模型过于理想化,在帧率较低且运动变化较大的场景中可能会跟踪丢失。
重定位跟踪


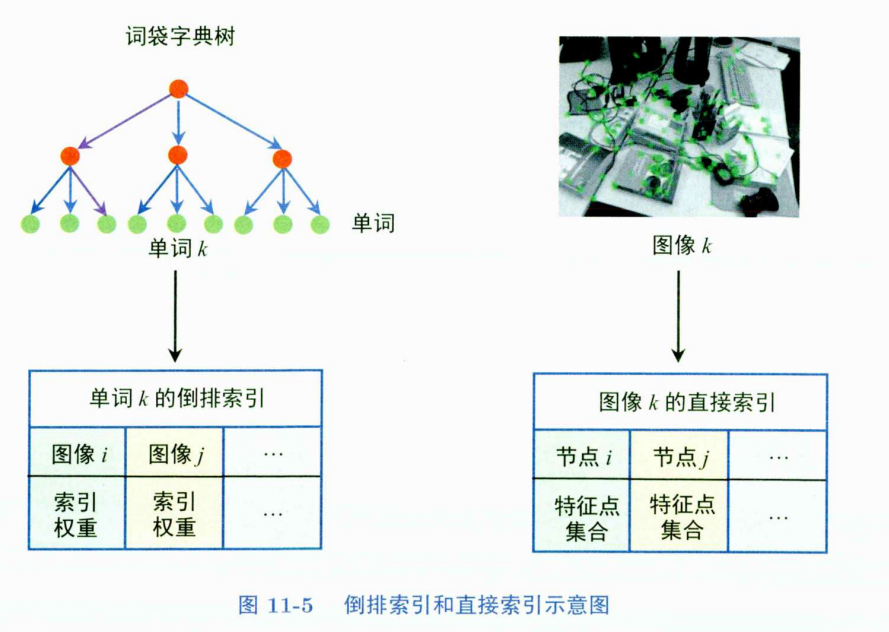



局部地图跟踪
参考关键帧跟踪、恒速模型跟踪、重定位跟踪——都称为第一阶段跟踪,它们的目的是保证能够“跟得上”,但因为用到的信息有限,所以得到的位姿可能不太准确。
跟踪的第二阶段——局部地图跟踪,它将当前帧的局部关键帧对应的局部地图点投影到该帧中,得到更多的特征点匹配关系,对第一阶段的位姿再进行优化,得到相对准确的位姿。
小白:ORB-SLAM2中跟踪部分有local map,还有一个线程叫 local mapping,这两个概念怎么区分呢?
- 师兄:虽然这两个名字取得有点类似,但是它们的功能差别很大。
- 首先,local map是指局部地图,局部地图来自局部关键帧对应的地图点,而局部关键帧包括当前普通帧的一级共视关键帧、二级共视关键帧及其子关键帧和父关键帧。local map 的目的是增加更多的投影匹配约束关系,仅优化当前帧的位姿,不优化局部关键帧,也不优化地图点。
- 其次,local mapping是指局部建图线程,用来处理跟踪过程中建立的关键帧,包括这些关键帧之间互相匹配生成新的可靠的地图点、一起优化当前关键帧及其共视关键帧的位姿和地图点。根据优化结果删除地图中不可靠的地图点、冗余的关键帧。local mapping 的目的是让已有的关键帧之间产生更多的联系,产生更多可靠的地图点,优化共视关键帧的位姿及其地图点,使得跟踪更稳定。这部分我们在第12章中细讲。
局部关键帧
void Tracking::UpdateLocalKeyFrames()
怎么确定局部关键帧?
为方便理解,我们先来看一个局部关键帧的示意图,如图11-8所示。当前帧F的局部关键帧包括:
- 能够观测到当前帧F中地图点的共视关键帧KF1、KF2,称为一级共视关键帧。
- 一级共视关键帧的共视关键帧(代码中取前10个共视程度最高的关键帧),比如图11-8中的KF1的共视关键帧为KF3、KF4,KF2的共视关键帧为KF5、KF6,称为二级共视关键帧。
- 一级共视关键帧的父关键帧和子关键帧。当前关键帧共视程度最高的关键帧称为父关键帧,反过来,当前关键帧称为对方的子关键帧。图 11-8中 KF7是KF1的父关键帧;反过来,KF1是KF7的子关键帧。一个关键帧只有一个父关键帧,但可以有多个子关键帧。
总结:图11-8中当前帧F的局部关键帧为一级共视关键帧KF1、KF2,二级共视关键帧KF3、KF4、KF5、KF6,一级共视关键帧的父子关键帧KF7、KF8。

局部地图点
void Tracking::UpdateLocalPoints()
小白:那局部地图点就是由局部关键帧对应的所有地图点组成的吧?
师兄:是的。图11-9所示是ORB-SLAM2在TUM 某个数据集上运行过程中的截图,其中绿色框表示当前帧,蓝色小三角形表示关键帧,蓝色虚线椭圆形框内的关键帧是当前帧的局部关键帧,这些局部关键帧对应的地图点在图11-9中标记为红色,所有红色地图点表示当前帧的局部地图点。
小白:从当前帧的朝向来看,它能看到的地图点很有限,就是两个绿色虚线箭头夹着的区域吧?红色的局部地图点所占的空间要大好多啊!甚至在当前帧的背面都有!
师兄:是的。当前帧观测到的地图点在两个绿色虚线箭头之间,这部分要远小于红色的局部地图点区域。这也是局部地图跟踪的意义所在。我们通过局部关键帧得到了比当前帧多得多的地图点。当然,这些地图点并不能全部用来匹配和优化,我们在11.4.3节中再讨论。

通过投影匹配得到更多的匹配点对
师兄:前面我们得到那么多局部特征点,就是为了和当前帧建立更多的匹配关系,这样在进一步进行BA优化时,通过更多的约束关系才能让位姿更加准确那么这些局部特征点都能用来投影吗?
显然不是。在图11-9中我们可以看到,虽然局部地图点的数量非常多,但是很多是不合格的,无法用来进行真正的搜索匹配。那么哪些点才能用来进行搜索匹配呢?如何筛选呢?
首先,当前帧的有效地图点已经通过第一阶段跟踪建立过匹配关系,所以在局部地图点中首先需要排除当前帧的地图点。
然后,剩下的地图点需要在当前帧的视野范围内才可以用于投影匹配。最后,设定搜索窗口的大小,将满足投影条件的局部地图点投影到当前帧中在投影点附近区域进行搜索匹配。这部分内容和前面讲的投影匹配原理类似,这里不再赘述。
师兄:前面留了一个尾巴,如何判断地图点是否在视野范围内?bool Frame::isInFrustum(MapPoint *pMP, float viewingCosLimit)
判断一个地图点在不在视野范围内要通关如下4个关卡:
(1)关卡1。将这个地图点变换到当前帧的相机坐标系下,只有深度值为正,才能继续下一步。
( 2)关卡2。将地图点投影到当前帧的像素坐标上,只有在图像有效范围内,才能继续下一步。
(3)关卡3。计算地图点到相机中心的距离,只有在有效距离范围内,才能继续下一步。
(4)关卡4。计算当前相机指向地图点的向量和地图点的平均观测方向的夹角,小于60°才能进入下一步。
局部地图跟踪源码解析
局部地图跟踪作为跟踪线程中的第二阶段跟踪,主要目的是增加更多的匹配关系,再次优化位姿,从而得到更准确的位姿。具体流程如下:
- 第一步,更新局部关键帧和局部地图点。局部关键帧包括能观测到当前帧的一级共视关键帧,这些一级共视关键帧的二级共视关键帧、子关键帧、父关键帧。将局部关键帧中所有的地图点作为局部地图点。
- 第二步,筛选局部地图点中新增的在视野范围内的地图点,投影到当前帧中进行搜索匹配,得到更多的匹配关系。
- 第三步,前面得到了更多的匹配关系,再一次进行BA优化(仅优化位姿),得到更准确的位姿。
- 第四步,更新当前帧地图点的背观测程度,并统计成功跟踪匹配的总数目。
- 第五步,根据成功跟踪匹配总数目及重定位情况决定是否跟踪成功。
函数:
void Tracking::Track()
- @brief Main tracking function. It is independent of the input sensor.
- track包含两部分:估计运动、跟踪局部地图
- Step 1:初始化
- Step 2:跟踪
- Step 3:记录位姿信息,用于轨迹复现
步骤:
-
track包含两部分:估计运动、跟踪局部地图
-
mState为tracking的状态,包括 SYSTME_NOT_READY, NO_IMAGE_YET, NOT_INITIALIZED, OK, LOST
如果图像复位过、或者第一次运行,则为NO_IMAGE_YET状态
如果是mState==NO_IMAGE_YET,说明还没有初始化mState = NOT_INITIALIZED;
-
step 1:地图初始化
-
如果地图没有初始化,则开始初始化操作
- 如果传感器为双目或RGBD相机,则使用
StereoInitialization(); - 如果传感器为单目,则使用
MonocularInitialization(); - 更新帧绘制器中存储的最新状态;如果初始化不过,则退出return ;
- 如果传感器为双目或RGBD相机,则使用
-
如果地图已初始化了,则开始下一步
-
判断是否为slam模式或者是纯定位模式?
-
如果是slam模式,则 Step 2:跟踪进入正常SLAM模式,有地图更新
-
判断是否可以正常跟踪,如果可以正常跟踪,则:
-
Step 2.1 检查并更新上一帧被替换的MapPoints 。(局部建图线程则可能会对原有的地图点进行替换.在这里进行检查)
CheckReplacedInLastFrame(); -
Step 2.2 运动模型是空的或刚完成重定位,则使用跟踪参考关键帧
// 用最近的关键帧来跟踪当前的普通帧 // 通过BoW的方式在参考帧中找当前帧特征点的匹配点 // 优化每个特征点都对应3D点重投影误差即可得到位姿 bOK = TrackReferenceKeyFrame();- 第一个条件,如果运动模型为空,说明是刚初始化开始,或者已经跟丢了
- 第二个条件,如果当前帧紧紧地跟着在重定位的帧的后面,我们将重定位帧来恢复位姿

-
否则,使用恒速模型跟踪,若恒速模型跟踪失败,则重新使用参考关键帧跟踪
// 用最近的普通帧来跟踪当前的普通帧 // 根据恒速模型设定当前帧的初始位姿 // 通过投影的方式在参考帧中找当前帧特征点的匹配点 // 优化每个特征点所对应3D点的投影误差即可得到位姿 bOK = TrackWithMotionModel(); if(!bOK) //根据恒速模型失败了,只能根据参考关键帧来跟踪 bOK = TrackReferenceKeyFrame();
-
-
如果不能正常跟踪,则只能进行重定位了,使用BOW搜索,EPNP求解位姿
bOK = Relocalization();
-
-
如果是仅定位模式跟踪,则Step 2:只进行跟踪tracking,局部地图不工作
-
如果跟丢了,只能重定位
bOK = Relocalization(); -
如果没有跟丢,则
-
如果此帧匹配了很多的MapPoints,跟踪很正常(mbvo==false),则使用恒速模型或参考关键帧跟踪
- 如果运动模型(及速度)不为空,则使用恒速模型跟踪
- 否则,则使用参考关键帧跟踪
-
如果此帧匹配了很少的MapPoints,少于10个,要跪的节奏,既做跟踪又做重定位
-
Step 2.3 当运动模型有效的时候,根据运动模型计算位姿
if(!mVelocity.empty()) { bOKMM = TrackWithMotionModel(); // 将恒速模型跟踪结果暂存到这几个变量中,因为后面重定位会改变这些变量 vpMPsMM = mCurrentFrame.mvpMapPoints; vbOutMM = mCurrentFrame.mvbOutlier; TcwMM = mCurrentFrame.mTcw.clone(); } -
Step 2.4 使用重定位的方法来得到当前帧的位姿
bOKReloc = Relocalization(); -
Step 2.5 根据前面的恒速模型、重定位结果来更新状态
-
如果恒速模型成功们重定位失败,则
- 重新使用之前存储的恒速模型结果
- 如果当前帧匹配的3D点很少,增加当前可视地图点的被观测次数
- 遍历每一个点,跟新当前帧的地图点被观测次数 for
- 如果这个特征点形成了地图点,并且也不是外点的时候,则增加能观测到该地图点的帧数
- 遍历每一个点,跟新当前帧的地图点被观测次数 for
-
else if 如果重定位成功了,增整个跟踪过程正常进行 (重定位与跟踪,更相信重定位)
mbVo=false -
只要恒速模型和重定位跟踪有一个成功了,我们就认为执行成功了
bOK = bOKReloc || bOKMM;
-
-
-
-
将最新的关键帧作为当前帧的参考关键帧
-
Step 3:在跟踪得到当前帧初始姿态后,现在对local map进行跟踪得到更多的匹配,并优化当前位姿。
前面只是跟踪一帧得到初始位姿,这里搜索局部关键帧、局部地图点,和当前帧进行投影匹配,得到更多匹配的MapPoints后进行Pose优化
-
如果是SLAM模式
-
如果每个函数执行成功,则进行局部地图跟踪

-
-
如果仅定位模式,
-
如果重定位成功且每个函数执行成功,则进入局部地图跟踪

-
-
根据上面操作来判断是否追踪成功
if(bOK) mState = OK; else mState=LOST; -
Step 4:更新显示线程中的图像、特征点、地图点等信息
-
只有在成功追踪时才考虑生成关键帧的问题。如果跟踪成功了,则
-
Step 5:跟踪成功,如果上一帧的相机位姿不为空,则通过其更新恒速运动模型中的速度
(mVelocity = Tcl = Tcw * Twl,表示上一帧到当前帧的变换, 其中 Twl = LastTwc)
-
否则,速度为空
-
更新显示(画图mpMapDrawer)中的位姿
-
Step 6:清除观测不到的地图点
-
Step 7:清除恒速模型跟踪中 UpdateLastFrame中为当前帧临时添加的MapPoints(仅双目和rgbd)
// 步骤6中只是在当前帧中将这些MapPoints剔除,这里从MapPoints数据库中删除 // 临时地图点仅仅是为了提高双目或rgbd摄像头的帧间跟踪效果,用完以后就扔了,没有添加到地图中 for(list<MapPoint*>::iterator lit = mlpTemporalPoints.begin(), lend = mlpTemporalPoints.end(); lit!=lend; lit++) { MapPoint* pMP = *lit; delete pMP; } // 这里不仅仅是清除mlpTemporalPoints,通过delete pMP还删除了指针指向的MapPoint // 不能够直接执行这个是因为其中存储的都是指针,之前的操作都是为了避免内存泄露 mlpTemporalPoints.clear(); -
Step 8:检测并插入关键帧,对于双目或RGB-D会产生新的地图点
if(NeedNewKeyFrame()) CreateNewKeyFrame(); -
Step 9 删除那些在bundle adjustment中检测为outlier的地图点
-
-
Step 10 如果初始化后不久就跟踪失败,并且relocation也没有搞定,只能重新Reset
if(mState==LOST) { //如果地图中的关键帧信息过少的话,直接重新进行初始化了 if(mpMap->KeyFramesInMap()<=5) { cout << "Track lost soon after initialisation, reseting..." << endl; mpSystem->Reset(); return; } } -
确保已经设置了参考关键帧
if(!mCurrentFrame.mpReferenceKF) mCurrentFrame.mpReferenceKF = mpReferenceKF; -
保存上一帧的数据,当前帧变上一帧
mLastFrame = Frame(mCurrentFrame);
-
-
Step 11:记录位姿信息,用于最后保存所有的轨迹
- 如果当前帧相机位姿不为空,则,计算相对位姿
Tcr = Tcw * Twr, Twr = Trw^-1,保存各种状态 - 如果当前帧相机位姿为空,说明跟踪失败,则相对位姿使用上一次值
- 如果当前帧相机位姿不为空,则,计算相对位姿
NeedNewKeyFrame()
- @brief 判断当前帧是否需要插入关键帧
- Step 1:纯VO模式下不插入关键帧,如果局部地图被闭环检测使用,则不插入关键帧
- Step 2:如果距离上一次重定位比较近,或者关键帧数目超出最大限制,不插入关键帧
- Step 3:得到参考关键帧跟踪到的地图点数量
- Step 4:查询局部地图管理器是否繁忙,也就是当前能否接受新的关键帧
- Step 5:对于双目或RGBD摄像头,统计可以添加的有效地图点总数 和 跟踪到的地图点数量
- Step 6:决策是否需要插入关键帧
- @return true 需要
- @return false 不需要
步骤:
首先考虑哪些情况下是不需要插入关键帧的,然后在考虑插入关键帧需要什么条件。
- 仅定位模式不插入关键帧
- 如果局部地图线程被闭环线程使用,则不插入关键帧
- 如果距离上一次重定位比较近,并且关键帧超出最大限制,则不插入关键帧
- 得到参考关键帧跟踪到的地图点数量(UpdateLocalKeyFrames 函数中会将与当前关键帧共视程度最高的关键帧设定为当前帧的参考关键帧)
- 查询局部地图线程是否繁忙,当前能否接受新的关键帧
- 对于双目或RGBD摄像头,统计成功跟踪的近点的数量,如果跟踪到的近点太少,没有跟踪到的近点较多,可以插入关键帧。
- 决策是否需要插入关键帧
- 设定比例阈值,当前帧和参考关键帧跟踪到点的比例,比例越大,越倾向于增加关键帧。(不同传感器需要的阈值不同)
- 1a很长时间没有插入关键帧,可以插入
- 1b满足插入关键帧的最小间隔并且localMapper处于空闲状态,可以插入
- 1c在双目,RGB-D的情况下当前帧跟踪到的点比参考关键帧的0.25倍还少,或者满足bNeedToInsertClose ( bNeedToInsertClose是判断双目或RGBD情况下:跟踪到的地图点中近点太少 同时 没有跟踪到的三维点太多,可以插入关键帧了。其是一个bool类型变量)
- 2和参考帧相比当前跟踪到的点太少 或者满足bNeedToInsertClose;同时跟踪到的内点还不能太少
- if((c1a||c1b||c1c)&&c2)
- 如果local mapping 空闲是可以插入关键帧
- 若不空闲
- 若传感器不是单目
- 若队列中关键帧数目不是很多,则可以插入
- 否则不能
- 否之不能
- 若传感器不是单目
- 否之不能
- 否之不能
bool Tracking::TrackReferenceKeyFrame()
- @brief 用参考关键帧的地图点来对当前普通帧进行跟踪
- Step 1:将当前普通帧的描述子转化为BoW向量
- Step 2:通过词袋BoW加速当前帧与参考帧之间的特征点匹配
- Step 3: 将上一帧的位姿态作为当前帧位姿的初始值
- Step 4: 通过优化3D-2D的重投影误差来获得位姿
- Step 5:剔除优化后的匹配点中的外点
- @return 如果匹配数超10,返回true
void Tracking::UpdateLastFrame()
-
@brief 更新上一帧位姿,在上一帧中生成临时地图点
-
单目情况:只计算了上一帧的世界坐标系位姿
-
双目和rgbd情况:选取有深度值的并且没有被选为地图点的点生成新的临时地图点,提高跟踪鲁棒性

步骤:
- 利用参考帧更新上一帧在世界坐标下的位姿。(这里的参考帧是上一普通帧的参考帧)Tlw = Tlr*Trw
- 如果上一帧为关键帧或者单目情况,则退出
- 对于双目或rgbd相机,为上一帧生成新的临时地图点。注意这些地图点只是用于跟踪,不加入到地图中,跟踪完后会删除
- 得到上一帧中具有有效深度值(z>0)的特征点(不一定是地图点),若没有,则退出;否之,则按照深度从小到大排序
- 从特征点中找到不是地图点的部分,这一步需要对每个特征点进行遍历
- 如果这个点对应在上一帧中的地图点没有,或者创建后就没有被观测到,那么就生成一个临时的地图点
- if 如果需要创建临时地图点
- 需要创建的点,包装为地图点。只是为了提高双目和RGBD的跟踪成功率,并没有添加复杂属性,因为后面会扔掉
- 将该特征点反投影到世界坐标系中,生成新的地图点
- 加入上一帧的地图点中
- 标记为临时添加的MapPoint,之后在CreateNewKeyFrame之前会全部删除,并未添加新的观测信息
- nPoints++;
- else 如果不需要创建临时地图点,则nPoints++;
- 如果地图点质量不好,停止创建地图点。停止新增临时地图点必须同时满足以下条件:
- 当前的点的深度已经超过了设定的深度阈值(35倍基线)
- nPoints(因为前面将特征点按照深度从小到大排序,这里记录已经计算了多少点)已经超过100个点,说明距离比较远了,可能不准确,停掉退出
bool Tracking::TrackWithMotionModel()
- @brief 根据恒定速度模型用上一帧地图点来对当前帧进行跟踪
- Step 1:更新上一帧的位姿;对于双目或RGB-D相机,还会根据深度值生成临时地图点
- Step 2:根据上一帧特征点对应地图点进行投影匹配
- Step 3:优化当前帧位姿
- Step 4:剔除地图点中外点
- @return 如果匹配数大于10,认为跟踪成功,返回true
步骤:
- 更新上一帧的位姿;对于双目或RGB-D相机,还会根据深度值生成临时地图点
- 根据之前估计的速度,和上一帧的位姿,用恒速模型得到当前帧的初始位姿
- 清空当前帧的地图点,设置特征匹配过程中的搜索半径
- 用上一帧地图点进行投影匹配,如果匹配点不够,则扩大搜索半径再来一次
- 如果还是不能够得到足够的匹配点,则认为跟踪失败,return false
- 如果跟踪成功,则
- 利用3D-2D 投影关系,优化当前帧位姿
- 遍历每个点,剔除地图点外点
- 如果该特征点找到了对应的地图点
- if 如果该点为外点,则清除它的所有关系
- else if 该地图点的观测次数 >0,则累加成功匹配到的地图点数目
- 如果该特征点找到了对应的地图点
- 如果处于纯定位模式下
- 如果成功追踪的地图点非常少,那么这里的mbVO标志就会置位
- mbVO = nmatchesMap<10
- return nmatches>20
- 匹配超过10个地图点就认为跟踪成功
bool Tracking::Relocalization()
- @details 重定位过程
- @return true
- @return false
- Step 1:计算当前帧特征点的词袋向量
- Step 2:找到与当前帧相似的候选关键帧
- Step 3:通过BoW进行匹配
- Step 4:通过EPnP算法估计姿态
- Step 5:通过PoseOptimization对姿态进行优化求解
- Step 6:如果内点较少,则通过投影的方式对之前未匹配的点进行匹配,再进行优化求解
步骤:
-
计算当前帧特征点的词袋向量
-
用词袋向量找到与当前帧相似的候选关键帧 (使用vector<KeyFrame*> KeyFrameDatabase::DetectRelocalizationCandidates(Frame *F) 函数)
-
遍历所有的候选关键帧,通过词袋进行快速匹配,用匹配结果初始化PnP Solve for 例对一个候选关键帧进行处理
- 判断该帧是否是坏帧,标记坏帧;否之则继续下面的操作
- 当前帧和候选关键帧用BoW进行快速匹配,匹配结果记录在vvpMapPointMatches[ i ],nmatches表示匹配的数目
- 如果当前帧的匹配数小于15,那么只能放弃这个关键帧;否之,继续下面操作
- 如果匹配数目够用,用匹配结果初始化EPnPsolver 。为什么用EPnP? 因为计算复杂度低,精度高
-
通过一系列操作,直到找到能够匹配上的关键帧。为什么搞这么复杂?答:是担心误闭环。
while(nCandidates>0 && !bMatch)-
遍历当前所有的候选关键帧,例 一个候选关键帧
-
是否标记为放弃? 若是,则continue
-
通过EPnP算法估计姿态,迭代5次
-
如果 bNoMore 为true 表示已经超过了RANSAC最大迭代次数,就放弃当前关键帧
-
如果相机位姿在ii中被计算了,则进入优化
-
如果EPnP 计算出了位姿,对内点进行BA优化
-
遍历所有内点
- 如果内点被标记
- 更新当前帧的关于该点的地图点信息
- 将地图点插入EPnP 里RANSAC后的内点的集合
- 否则更新当前帧的关于该点的地图点信息为NULL
- 如果内点被标记
-
只优化位姿,不优化地图点的坐标,返回的是内点的数量
-
如果优化之后的内点数目不多,跳过了当前候选关键帧,但是却没有放弃当前帧的重定位
-
删除外点对应的地图点
-
(开始新的步骤,下面都属于该步4.3)如果内点较少,则通过投影的方式对之前未匹配的点进行匹配,再进行优化求解。前面的匹配关系是用词袋匹配过程得到的
-
如果nGood<50
- 通过投影的方式将关键帧中未匹配的地图点投影到当前帧中, 生成新的匹配SearchByProjection( )
- 如果通过投影过程新增了比较多的匹配特征点对(if(nadditional+nGood>=50))
- 根据投影匹配的结果,再次采用3D-2D pnp BA优化位姿
- 4.4 如果BA后内点数还是比较少(<50)但是还不至于太少(>30),可以挽救一下, 最后垂死挣扎 。重新执行上一步 4.3的过程,只不过使用更小的搜索窗口 。这里的位姿已经使用了更多的点进行了优化,应该更准,所以使用更小的窗口搜索
- if(nGood>30 && nGood<50)
- 用更小窗口、更严格的描述子阈值,重新进行投影搜索匹配
- 将当前帧的每个地图点都插入sFound中
- 通过投影的方式将关键帧中未匹配的地图点投影到当前帧中, 生成新的匹配SearchByProjection( )
- if(nGood+nadditional>=50)(如果成功挽救回来,匹配数目达到要求,最后BA优化一下,更新地图点)
- 如果还是不能够满足就放弃了
-
if(nGood>=50) 如果对于当前的候选关键帧已经有足够的内点(50个)了,那么就认为重定位成功
// 如果对于当前的候选关键帧已经有足够的内点(50个)了,那么就认为重定位成功 if(nGood>=50) { bMatch = true; // 只要有一个候选关键帧重定位成功,就退出循环,不考虑其他候选关键帧了 break; }
-
-
-
-
若还是没有匹配上,则重定位失败,return false;
-
否则,如果匹配上了,说明当前帧重定位成功了(当前帧已经有了自己的位姿),记录成功重定位帧的id,防止短时间多次重定位
void Tracking::UpdateLocalKeyFrames()
- @brief 跟踪局部地图函数里,更新局部关键帧
- 方法是遍历当前帧的地图点,将观测到这些地图点的关键帧和相邻的关键帧及其父子关键帧,作为mvpLocalKeyFrames
- Step 1:遍历当前帧的地图点,记录所有能观测到当前帧地图点的关键帧
- Step 2:更新局部关键帧(mvpLocalKeyFrames),添加局部关键帧包括以下3种类型
- 类型1:能观测到当前帧地图点的关键帧,也称一级共视关键帧
- 类型2:一级共视关键帧的共视关键帧,称为二级共视关键帧
- 类型3:一级共视关键帧的子关键帧、父关键帧
- Step 3:更新当前帧的参考关键帧,与自己共视程度最高的关键帧作为参考关键帧
步骤:
-
遍历当前帧的地图点,记录所有能观测到当前帧地图点的关键帧
-
获得一个地图点,判断其是否为好点
-
如果该地图点是好点
- 得到观测到该地图点的关键帧和该地图点在关键帧中的索引
- 由于一个地图点可以被多个关键帧观测到,因此对于每一次观测,都对观测到这个地图点的关键帧进行累计投票(其中变量keyframeCounter 第一个参数表示某个关键帧,第2个参数表示该关键帧看到了多少当前帧(mCurrentFrame)的地图点,也就是共视程度)
-
如果该地图点是坏点,则将该地图点置为NULL
mCurrentFrame.mvpMapPoints[i]=NULL;
-
-
更新局部关键帧(mvpLocalKeyFrames),添加局部关键帧有三种类型,所有要先请客局部关键帧,然后先申请3倍内存,不够后面再加
-
Step 2.1,类型1:能观测到当前帧地图点的关键帧作为局部关键帧 (将邻居拉拢入伙)(一级共视关键帧)
-
遍历1中得到的关键帧keyframeCounter ,判断其好坏。
对好的帧 寻找最大观测数目的关键帧 ,并将好的帧添加到局部关键帧列表里,并标记该帧为当前帧的局部关键帧,防止重复添加关键帧。
-
-
Step 2.2,遍历一级共视关键帧,寻找更多的局部关键帧 for,以一个帧为例
-
如果处理的局部关键帧数量超过80,则结束,退出循环。
-
类型2:一级共视关键帧的共视(前10个)关键帧,称为二级共视关键帧(将邻居的邻居拉拢入伙),如果共视帧不足10帧,那么就返回所有具有共视关系的关键帧
-
获取该一级关键帧的前10个共视关键帧(为二级关键帧)(vNeighs 是按照共视程度从大到小排列)
const vector<KeyFrame*> vNeighs = pKF->GetBestCovisibilityKeyFrames(10); -
从大到小遍历这些共视关键帧
-
判断该帧是否为坏帧,排除坏帧
-
判断该帧是否已被添加为局部关键帧,若没有,则继续
if(pNeighKF->mnTrackReferenceForFrame!=mCurrentFrame.mnId) -
将该帧添加到局部关键帧中,并标记该帧,break(在代码中有break,找到一个就直接跳出来for循环)
-
-
-
类型3:将一级共视关键帧的子关键帧作为局部关键帧(将邻居的孩子们拉拢入伙)
- 获取该帧的子关键帧
- 遍历每一个子关键帧,for
- 判断该帧是否为坏帧,排除坏帧
- 判断该帧是否已被添加为局部关键帧,若没有,则继续
- 将该帧添加到局部关键帧中,并标记该帧,break(在代码中有break,找到一个就直接跳出来for循环)
-
类型3:将一级共视关键帧的父关键帧作为局部关键帧(将邻居的父母们拉拢入伙)
- 如果父节点存在,则继续
- 判断该帧是否已被添加为局部关键帧,若没有,则继续
- 将该帧添加到局部关键帧中,并标记该帧,break(在代码中有break,找到一个就直接跳出来for循环,这里应该是bug)
-
-
-
更新当前帧的参考关键帧,与自己共视程度最高的关键帧(其实就是第一步中所拥有共同地图点最多的一级共视关键帧)作为参考关键帧
void Tracking::UpdateLocalPoints()
- @brief 更新局部关键点。先把局部地图清空,然后将局部关键帧的有效地图点添加到局部地图中
步骤:
- 情况局部地图点
- 遍历局部关键帧
mvpLocalKeyFrames,以一个帧为例- 获取该帧的所有地图点
- 遍历每个地图点, for
- 如果该地图点不存在,则continue
- 判断该点是否已被添加过,如果已经添加过,则continue
- 如果该点是坏点,则continue
- 将该地图点添加为局部地图点,并且标记该地图点,防止重复添加局部地图点
void Tracking::SearchLocalPoints()
- @brief 用局部地图点进行投影匹配,得到更多的匹配关系
- 注意:局部地图点中已经是当前帧地图点的不需要再投影,只需要将此外的并且在视野范围内的点和当前帧进行投影匹配
步骤:
-
遍历当前帧的地图点,标记这些地图点不参与之后的投影搜索匹配 ,for,以一个点为例
- 获取当前帧的地图点
- 判断该点是否存在,如果存在,则继续
- 判断该点是否为坏点,如果为坏点,则置为NULL
*vit = static_cast<MapPoint*>(NULL); - 如果为好点,则
- 更新能观测到该点的帧数加1(被当前帧观测了)
- 标记该点被当前帧观测到
- 标记该点在后面搜索匹配时不被投影,因为已经有匹配了
-
判断所有局部地图点中除当前帧地图点外的点,是否在当前帧视野范围内
- 如果该点已被当前帧观测到,那么肯定在视野范围内,则跳过
- 如果该点是坏点,则跳过
- 判断地图点是否在在当前帧视野内,如果在,则
- 观测到该点的帧数加1
- 只有在视野范围内的地图点才参与之后的投影匹配
-
如果需要进行投影匹配的点的数目大于0,就进行投影匹配,增加更多的匹配关系
-
初始化ORBmatcher,设定阈值,当RGBD相机输入的时候,搜索的阈值会变得稍微大一些
-
如果不久前进行过重定位,那么进行一个更加宽泛的搜索,阈值需要增大
-
投影匹配得到更多的匹配关系
matcher.SearchByProjection(mCurrentFrame,mvpLocalMapPoints,th);
-
void Tracking::UpdateLocalMap()
- @brief 更新LocalMap
* - 局部地图包括:
- 1、K1个关键帧、K2个临近关键帧和参考关键帧
- 2、由这些关键帧观测到的MapPoints
void Tracking::UpdateLocalMap()
{
// This is for visualization
// 设置参考地图点用于绘图显示局部地图点(红色)
mpMap->SetReferenceMapPoints(mvpLocalMapPoints);
// Update
// 用共视图来更新局部关键帧和局部地图点
UpdateLocalKeyFrames();
UpdateLocalPoints();
}
bool Tracking::TrackLocalMap()
- @brief 用局部地图进行跟踪,进一步优化位姿
-
- 更新局部地图,包括局部关键帧和关键点
-
- 对局部MapPoints进行投影匹配
-
- 根据匹配对估计当前帧的姿态
-
- 根据姿态剔除误匹配
- @return true if success
- Step 1:更新局部关键帧mvpLocalKeyFrames和局部地图点mvpLocalMapPoints
- Step 2:在局部地图中查找与当前帧匹配的MapPoints, 其实也就是对局部地图点进行跟踪
- Step 3:更新局部所有MapPoints后对位姿再次优化
- Step 4:更新当前帧的MapPoints被观测程度,并统计跟踪局部地图的效果
- Step 5:决定是否跟踪成功
步骤:
-
Step 1:更新局部关键帧mvpLocalKeyFrames 和局部地图点 mvpLocalMapPoints
void Tracking::UpdateLocalMap() -
Step 2:筛选局部地图中新增的在视野范围内的地图点,投影到当前帧搜索匹配,得到更多的匹配关系
SearchLocalPoints(); -
Optimize Pose
在这个函数之前,在 Relocalization、TrackReferenceKeyFrame、TrackWithMotionModel 中都有位姿优化,
Step 3:前面新增了更多的匹配关系,BA优化得到更准确的位姿
Optimizer::PoseOptimization(&mCurrentFrame); -
Step 4:更新当前帧的地图点被观测程度,并统计跟踪局部地图后匹配数目
-
遍历当前帧的每一个特征点 for
-
如果特征点对应的地图点存在,则继续下面的操作
-
判断当前帧的地图点是否可以被当前帧观测到
-
if 如果可以观测到,则
-
该地图点被观测统计量加1
-
查看当前是否是在纯定位过程
-
if 若没有不是纯定位过程,则
-
如果该地图点被相机观测数目nObs大于0,匹配内点计数+1
nObs: 被观测到的相机数目,单目+1,双目或RGB-D则+2
-
-
如果是纯定位过程,则记录当前帧跟踪到的地图点数目,用于统计跟踪效果
-
-
-
else if 传感器为双目,则删除这个点
-
-
-
-
Step 5:根据跟踪匹配数目及重定位情况决定是否跟踪成功
- 如果最近刚刚发生了重定位,那么至少成功匹配50个点才认为是成功跟踪,如果失败,则返回false
- 如果是正常的状态话只要跟踪的地图点大于30个就认为成功了,如果失败,则返回false;否之,则返回true
Viewer.h
参数:
函数:
附录

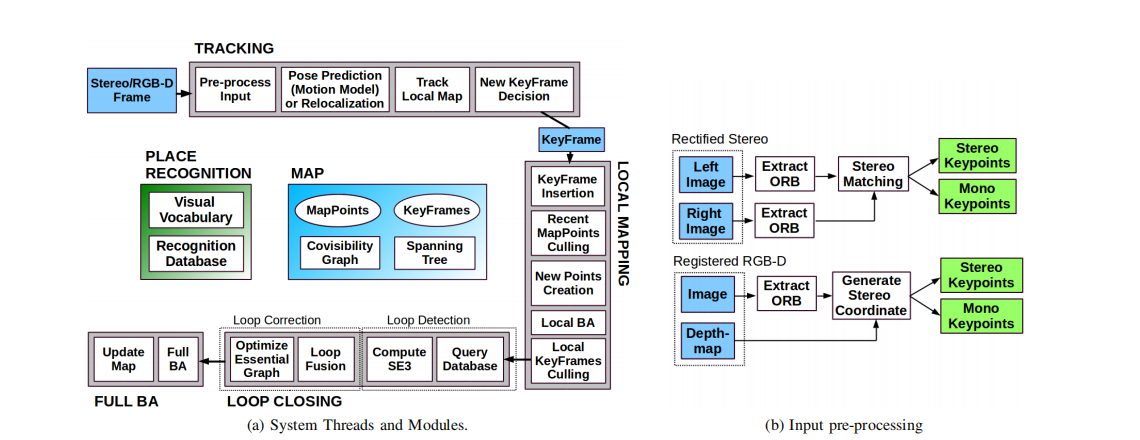

链接
从零开始一起学习SLAM | 相机成像模型 (qq.com)
从零开始一起学习SLAM | 神奇的单应矩阵 (qq.com)
相机模型中四个坐标系的关系 - 知乎 (zhihu.com)
常见的几类矩阵(正交矩阵、酉矩阵、正规矩阵等)_NeverMoreH的博客-CSDN博客
一文让你通俗理解奇异值分解 - 知乎 (zhihu.com)
【图像处理】双线性插值法扩展图像像素及其代码实现(亚像素) - 知乎 (zhihu.com)
本质矩阵E= t^ R ( t^ 表示t的反对称矩阵 )
基础矩阵 F = K − T E K − 1 \mathbf{F}=\mathbf{K^{-T} } \mathbf{E} \mathbf{K^{-1}} F=K−TEK−1
























 1716
1716

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








