一.实数理论
1.实数
(1)定义:
有理数和无理数统称实数;其中有理数可用分数形式 p q \frac{p}{q} qp(p,q∈Z,q≠0)表示,也可用有限10进制小数/无限10进制循环小数表示;而无限10进制不循环小数称为无理数
(2)实数的无限小数表达式:
- 又称为正规表示,作用是把有限小数也表示为无限小数
- 这种表示是唯一的
对正有限小数(包括正整数)x,当x=a0.a1···an(0≤ai≤9,ai∈Z,i=1,2···n,an≠0,a0为非负整数)时,记x=a0.a1···(an-1)999···
特别地,当x=a0为正整数时,记x=(a0-1).999···
例如:2.001记为2.000999···
对于负有限小数(包括负整数)y,则先将-y表示为无限小数,再在所得的无限小数前加负号
例如:-8记为-7.999···
规定数0表示为0.000···
(3)不足近似与过剩近似:
设x=a0.a1···an···为非负实数,称有理数xn=a0.a1···an为x的n位不足近似,而有理数 x − \stackrel{\mathrm{-}}{x} x−n=xn+( 1 10 \frac{1}{10} 101)n称为x的n位过剩近似(n=0,1···)
对于负实数x=-a0.a1···an···,其n位不足近似与过剩近似分别规定为xn=-a0.a1···an-( 1 10 \frac{1}{10} 101)n与 x − \stackrel{\mathrm{-}}{x} x−n=-a0.a1···an
当n增大时,xn不减,即x0≤x1≤···; x − \stackrel{\mathrm{-}}{x} x−n不增,即 x − \stackrel{\mathrm{-}}{x} x−0≥ x − \stackrel{\mathrm{-}}{x} x−1≥···
2.实数的大小关系
(1)定义:
对非负实数x=-a0.a1···an···与y=-b0.b1···bn···,(a0,b0为非负整数,0≤ak,bk≤9,ak,bk∈Z,k=1.2···),若有ak=bk(k=0,1···),则称x与y相等,记作x=y;若a0>b0或∃非负整数L使ak=bk(k=0,1···L)而aL+1>bL+1,则称x大于y或y小于x,记作x>y或y<x
对负实数x,y,若按上述规定有-x=-y与-x>-y,则分别称x=y与x<y(或y>x)
规定∀非负实数大于∀负实数
(2)命题:
设x=-a0.a1···an···与y=-b0.b1···bn···为2个实数,则x>y等价于:∃非负整数n,使xn> y − \stackrel{\mathrm{-}}{y} y−n
3.实数与实数集的性质:
记全体实数构成的集合为实数集,记为R
1.R对四则运算是封闭的,即∀2个实数的和/差/积/商(除数不为0)仍是实数
1.1有理数集和复数集对四则运算也是封闭的
2.实数集是有序的,即∀2个实数a,b必满足且只满足下述3个关系之一:a<b,a=b,a>b
3.实数的大小关系具有传递性,即a>b,b>c⇒a>c
4.实数具有阿基米德性(又称阿基米德公理,Archimedes Axiom),即对∀a,b∈R,若b>a>0,则∃∈Z+,使na>b
5.R具有稠密性,即∀2个不相等的实数间必有其他实数,且既有有理数,又有无理数
6.R与数轴上的点间存在一一对应关系,这反映了实数的完备性
4.绝对值
(1)定义:
实数a的绝对值记为|a|,定义为|a|=a(a≥0)或|a|=-a(a<0)
从数轴上看,|a|就是a到原点O的距离
(2)性质:
1.|a|=|-a|
2.当且仅当a=0时有|a|=0
3.-|a|≤a≤|a|
4.|a|<h⇔-h<a<h,|a|≤h⇔-h≤a≤h(h>0)
5.对∀a,b∈R,有|a|-|b|≤|a±b|≤|a|+|b|(三角不等式)
6.|ab|=|a||b|
7.| a b \frac{a}{b} ba|= ∣ a ∣ ∣ b ∣ \frac{|a|}{|b|} ∣b∣∣a∣(b≠0)
二.数集
1.区间
(1)区间:
设a,b∈R,称数集{x|a<x<b}为开区间,记为(a,b);称数集{x|a≤x≤b}为闭区间,记为[a,b];称数集{x|a<x≤b}和{x|a≤x<b}为半开半闭区间,记为(a,b]和[a,b);以上几类区间统称有限区间
满足关系式x≥a的全体实数的集合记作[a,+∞);类似地,有(-∞,a],(-∞,a),(a,+∞);以上几类区间统称无限区间
有限区间和无限区间统称区间
(2)邻域:
设a∈R,ζ>0,满足|x-a|<ζ的全体实数的集合称为点a的ζ邻域,记为U(a;ζ)或U(a),即有U(a;ζ)={x||x-a|<ζ}=(a-ζ,a+ζ);a的空心邻域(去心邻域)定义为U°(a;ζ)={x|0<|x-a|<ζ};a的右邻域U+(a;ζ)=[a,a+ζ),简记为U+(a);a的左邻域U-(a;ζ)=(a-ζ,a],简记为U-(a);a的左去心邻域U°-(a;ζ)=(a-ζ,a),简记为U°-(a);a的右去心邻域U°+(a;ζ)=(a,a+ζ),简记为U°+(a)
∞邻域U(∞)={x||x|>M},其中M为充分大的正数(下同);+∞邻域U(+∞)={x|x>M};-∞邻域U(-∞)={x|x<-M}
2.有界集
(1)定义:
设S为R中的1个数集,若∃数M(L),使对一切x∈S,都有x≤M(x≥L),则称S有上界(下界),M(L)为S的1个上界(下界)
若S既有上界又有下界,则称S为有界集;若S不是有界集,则称S为无界集
(2)确界:
设S为R中的1个数集,若数η满足:①对∀x∈S,有x≤η ②对∀α<η,∃x0∈S,使x0>α,即η是S的最小上界;则称η为S的(正常)上确界,记作η=sup S
设S为R中的1个数集,若数ξ满足:①对∀x∈S,有x≥ξ ②对∀β>ξ,∃x0∈S,使x0>β,即ξ是S的最大下界;则称η为S的(正常)下确界,记作ξ=inf S
上确界和下确界合称确界
如果上(下)确界∃,则必定唯一;若S∃上确界和下确界,则inf S≤sup S
S的确界可能属于也可能不属于S
(3)确界原理(定理1.1):
设S为非空数集,若S有上界,则S必有上确界;若S有下界,则S必有下确界

(4)推广确界与确界原理:
若把±∞补充到实数集中,并规定∀实数a与之的关系为:a<+∞,a>-∞,-∞<+∞,则确界可扩充为:若数集S无上界,则定义+∞为S的非正常上确界,记sup S=+∞;若S无下界,则定义-∞为S的非正常下确界,记inf S=-∞
∀非空数集必有上下确界(正常的或非正常的)
三.函数
1.映射:
如果2个集合A与B间存在着对应法则 f f f,使得对于A中的每个元素a,在B中总∃唯一的1个元素b与之对应,就称 f f f为从A到B的1个映射,记作 f : A → B f:A→B f:A→B
其中,b称为a在 f f f下的像,记作 b = f ( a ) b=f(a) b=f(a);a称为b在 f f f下的1个原像
集合A称为映射 f f f的定义域(domain),集合B称为映射 f f f的陪域(codomain,或上域,或到达域)
A中所有元素的像的集合称为映射 f f f的值域(range,或像集),记作 f ( A ) = { f ( a ) ∣ a ∈ A } 或 I m f f(A)=\{f(a)|a∈A\}或Im f f(A)={f(a)∣a∈A}或Imf
如果 f ( A ) = B f(A)=B f(A)=B,则称 f f f为1个满射;如果A中不同元素在 f f f下的像不同,则称 f f f为1个单射;如果 f f f既是单射又是满射,则称 f f f为1个双射(或一一对应)
如果映射 f , g f,g f,g的定义域/对应法则/陪域都相同,则称这2个映射相等,记作 f = g f=g f=g
2.函数定义:
给定2个数集D和M,若有对应法则f,使对∀x∈D,都有唯一的y∈M与之对应,则称f是定义在D上的函数,记作f:D→M;D称为函数f的定义域,x对应的y称为f在x处的函数值,常记为f(x);全体函数值的集合f(D)称为f的值域;x称为自变量,y称为因变量
注意:
①M常用R来代替,因此D和f是确定函数的2个主要因素,所以,常用y=f(x)(x∈D)表示1个函数;2个函数相同,指的是它们拥有相同的D和f(对应法则而非法则的表达形式),如f(x)=1和g(x)=1(x>0)不同,而φ(x)=|x|和ρ(x)= x 2 \sqrt {x^2} x2相同
②D常取使函数有意义的自变量的全体,称为存在域,此时D可省略
③f给出了D到M的单值对应,也称映射,对于a∈D,f(a)为映射f下a的象,a称为f(a)的1个原象
④对每个x∈D,如果只有1个y与之对应,这样的函数称为单值函数;如果可以有多个y与之对应,称为多值函数;后文的函数均指单值函数
⑤严格来说D可以不是数集,而是其他集合(如点集),但之后讨论的都是定义在数集上的函数
⑥暂时不考虑定义域为空集的函数(称为空函数)
可证明空函数是单射;但在 M ≠ Φ M≠Φ M=Φ时,空函数不是满射;因此空函数不是双射
3.分段函数:
指那些在定义域发不同部分用不同的公式表达的函数,如:
s g n x = { 1 ( x > 0 ) 0 ( x = 0 ) − 1 ( x < 0 ) sgnx= \begin{cases} 1\quad&(x>0)\\ 0\quad&(x=0)\\ -1\quad&(x<0) \end{cases} sgnx=⎩⎪⎨⎪⎧10−1(x>0)(x=0)(x<0)
该函数称为符号函数
4.函数的四则运算:

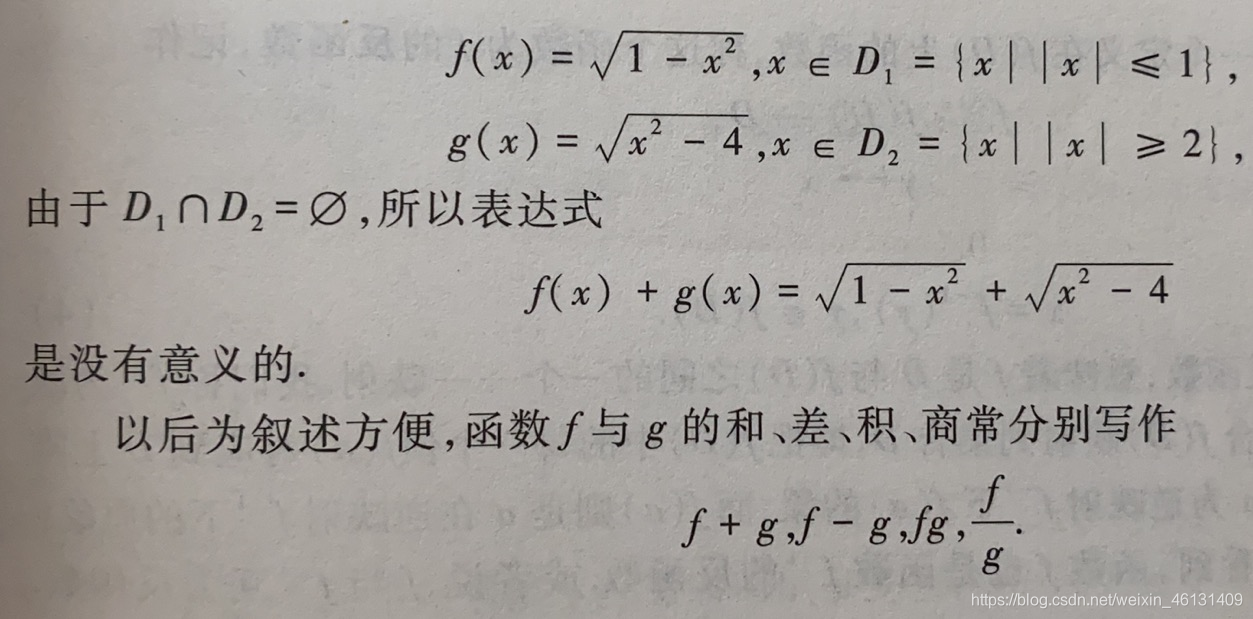
5.复合函数:

6.反函数:


7.初等函数
(1)基本初等函数:
基本初等函数包括:
①常量函数:y=c(c为常数)
②幂函数:y=xα(α为实数)
③指数函数:y=ax(a>0,a≠1)
④对数函数:y=logax(a>0,a≠1)
⑤三角函数:y=sin x,y=cos x,y=tan x,y=cot x
⑥反三角函数:y=arcsin x,y=arccos x,y=arctan x,y=arccot x
(2)扩展幂函数与指数函数的定义:

(3)初等函数:
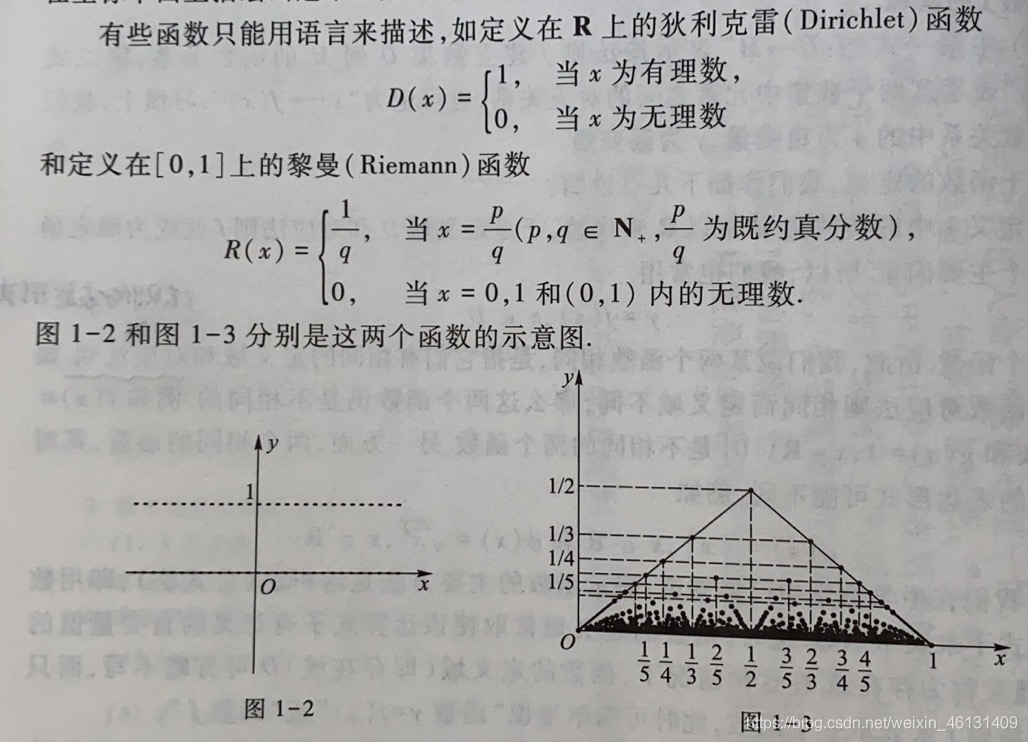
由基本初等函数经过有限次四则运算与复合运算所得的函数,称为初等函数;其他函数统称为非初等函数,如狄利克雷函数与黎曼函数
四.某些具有特殊性质的函数
1.有界函数:

2.单调函数:

定理1.2:设y=f(x)(x∈D)为严格增(减)函数,则f必有反函数f-1,且f-1在其定义域f(D)上也是严格增(减)函数
3.奇函数与偶函数:

4.周期函数:

四.实数的完备性
1.实数集完备性的基本定理

(1)区间套定理:
定理7.1:若 { [ a n , b n ] } \{[a_n,b_n]\} {[an,bn]}是1个区间套,则在实数系中∃唯一1点 ξ \xi ξ,使得 ξ ∈ [ a n , b n ] ( n = 1 , 2... ) \xi∈[a_n,b_n](n=1,2...) ξ∈[an,bn](n=1,2...),即 a n ≤ ξ ≤ b n ( n = 1 , 2... ) a_n≤\xi≤b_n(n=1,2...) an≤ξ≤bn(n=1,2...)
各区间均为闭区间时,才能保证该定理成立;对开区间列,可能不成立,如对 { ( 0 , 1 n ) } \{(0,\frac{1}{n})\} {(0,n1)}就不成立
推论:若 ξ ∈ [ a n , b n ] ( n = 1 , 2... ) \xi∈[a_n,b_n](n=1,2...) ξ∈[an,bn](n=1,2...)是区间套 { [ a n , b n ] } \{[a_n,b_n]\} {[an,bn]}确定的点,则对 ∀ ε > 0 , ∃ N > 0 , ∀ε>0,∃N>0, ∀ε>0,∃N>0,使当 n > N n>N n>N,有 [ a n , b n ] ⊂ U ( ξ ; ε ) [a_n,b_n]\subset U(\xi;ε) [an,bn]⊂U(ξ;ε)
用定理7.1推出连续函数根的存在性定理:
(2)魏尔斯特拉斯聚点定理(Weierstrass Accumulative Point Principle):
聚点的另2个等价定义如下:
定理7.2:实轴上的∀有界无限点集S至少有1个聚点
(3)海涅-博雷尔有限覆盖定理(Heine-Borel Theorem):

定理7.3:设H为[a,b]上的1个无限开覆盖,则从H中可选出有限个开区间来覆盖[a,b]
该定理仅对闭区间[a,b]成立,对开区间不一定成立;如开区间集合 ( 1 n + 1 , 1 ) ( n = 1 , 2... ) 和 开 区 间 ( 0 , 1 ) {(\frac{1}{n+1},1)}(n=1,2...)和开区间(0,1) (n+11,1)(n=1,2...)和开区间(0,1)
用定理7.3证明闭区间上连续函数的有界性定理:
(4)实数完备性基本定理间的等价性:
参见:
http://www.360doc.com/document/18/0319/21/32929879_738532695.shtml
在实数系中有关实数完备性的6个基本定理是等价的,可从其中任何1个推出另外5个
1⇒2:见 极限.一.5.(2) 部分,即定理2.9的证明
2⇒3:见 四.1.(1) 部分,即定理7.1的证明
3⇒4:见 四.1.(3) 部分,即定理7.3的证明
4⇒5:
6⇒1:
2.上极限与下极限
(1)数列的聚点:

注1:此处仍然不区分实数与实数轴上的点,因此点列的聚点等同于数列的聚点,数列或点列的聚点也称极限点
(2)定理7.4:
有界点列(或数列){xn}至少有1个聚点,且存在最大聚点和最小聚点
(3)上极限与下极限:
定理7.5:对任何有界数列{xn},有 lim n → ∞ ‾ x n ≤ lim n → ∞ ‾ x n \overline{\displaystyle\lim_{n \to \infty}}{x_n}≤\displaystyle\lim_{\overline{n \to \infty}}{x_n} n→∞limxn≤n→∞limxn
定理7.6: lim n → ∞ x n = A \displaystyle\lim_{n \to \infty}{x_n}=A n→∞limxn=A的充要条件是: lim n → ∞ ‾ x n = lim n → ∞ ‾ x n = A \overline{\displaystyle\lim_{n \to \infty}}{x_n}=\displaystyle\lim_{\overline{n \to \infty}}{x_n}=A n→∞limxn=n→∞limxn=A
(4)上(或下)极限的判定:
定理7.7:设{xn}为有界数列:
(Ⅰ) A ‾ \overline{A} A为{xn}上极限的充要条件是:对∀ε>0,①∃N>0,使当n>N,有 x n < A ‾ + ε x_n<\overline{A}+ε xn<A+ε ②∃子列 x n k , x n k > A ‾ − ε ( k = 1 , 2... ) {x_{n_k}},x_{n_k}>\overline{A}-ε(k=1,2...) xnk,xnk>A−ε(k=1,2...)
(Ⅱ) A ‾ \underline{A} A为{xn}下极限的充要条件是:∀ε>0,①∃N>0,使当n>N,有 x n > A ‾ − ε x_n>\underline{A}-ε xn>A−ε ②∃子列 x n k , x n k < A ‾ + ε ( k = 1 , 2... ) {x_{n_k}},x_{n_k}<\underline{A}+ε(k=1,2...) xnk,xnk<A+ε(k=1,2...)
定理7.7’(定理7.7的另1种形式):设{xn}为有界数列:
(Ⅰ) A ‾ \overline{A} A为{xn}上极限的充要条件是:对 ∀ α > A ‾ ∀α>\overline{A} ∀α>A,{xn}中大于α的项至多有有限个;对 ∀ β < A ‾ ∀β<\overline{A} ∀β<A,{xn}中大于β的项有无限多个
(Ⅱ) A ‾ \underline{A} A为{xn}下极限的充要条件是:对 ∀ β < A ‾ ∀β<\underline{A} ∀β<A,{xn}中小于β的项至多有有限个;对 ∀ α > A ‾ ∀α>\overline{A} ∀α>A,{xn}中小于α的项有无限多个
定理7.9:设{xn}为有界数列:
(Ⅰ) A ‾ \overline{A} A是{xn}上极限的充要条件是: A ‾ = lim n → ∞ s u p { x k } ( k ≥ n ) \overline{A}=\displaystyle\lim_{n \to \infty}{sup\{x_k\}}(k≥n) A=n→∞limsup{xk}(k≥n)
(Ⅱ) A ‾ \underline{A} A是{xn}下极限的充要条件是: A ‾ = lim n → ∞ i n f { x k } ( k ≥ n ) \underline{A}=\displaystyle\lim_{n \to \infty}{inf\{x_k\}}(k≥n) A=n→∞liminf{xk}(k≥n)
有些教材上使用上述2式作为上极限和下极限的定义
(5)上(或下)极限的性质:
上(或下)极限的保不等式性(定理7.8):设有界数列{an},{bn}满足:∃N0>0,当n>N0时有an≤bn,则 lim n → ∞ ‾ a n ≤ lim n → ∞ ‾ b n , lim n → ∞ ‾ a n ≤ lim n → ∞ ‾ b n \overline{\displaystyle\lim_{n \to \infty}}{a_n}≤\overline{\displaystyle\lim_{n \to \infty}}{b_n},\displaystyle\lim_{\overline{n \to \infty}}{a_n}≤\displaystyle\lim_{\overline{n \to \infty}}{b_n} n→∞liman≤n→∞limbn,n→∞liman≤n→∞limbn特别地,若α,β为常数,又∃N0>0,当n>N0时有α≤an≤β,则 α ≤ lim n → ∞ ‾ a n ≤ lim n → ∞ ‾ a n ≤ β α≤\displaystyle\lim_{\overline{n \to \infty}}{a_n}≤\overline{\displaystyle\lim_{n \to \infty}}{a_n}≤β α≤n→∞liman≤n→∞liman≤β
定理7.10:设{an},{bn}为有界数列,则: lim n → ∞ ‾ ( a n + b n ) ≤ lim n → ∞ ‾ a n + lim n → ∞ ‾ b n \overline{\lim_{n\to\infty}}{(a_n+b_n)}≤\overline{\lim_{n\to\infty}}{a_n}+\overline{\lim_{n\to\infty}}{b_n} n→∞lim(an+bn)≤n→∞liman+n→∞limbn特别地,若 lim n → ∞ a n ( 1 ) \displaystyle{\lim_{n\to\infty}}{a_n}\qquad(1) n→∞liman(1)存在,则: lim n → ∞ ‾ ( a n + b n ) = lim n → ∞ ‾ a n + lim n → ∞ ‾ b n = lim n → ∞ a n + lim n → ∞ ‾ b n ( 2 ) \overline{\lim_{n\to\infty}}{(a_n+b_n)}=\overline{\lim_{n\to\infty}}{a_n}+\overline{\lim_{n\to\infty}}{b_n}=\lim_{n\to\infty}{a_n}+\overline{\lim_{n\to\infty}}{b_n}\qquad(2) n→∞lim(an+bn)=n→∞liman+n→∞limbn=n→∞liman+n→∞limbn(2)
(6)非正常上(或下)极限:
若该定义中的a允许是非正常点±∞,则定理7.4可扩充为:任一点列(或数列){xn}至少有1个聚点,且存在最大聚点和最小聚点
无上(下)界点列的最大(小)聚点为+∞(-∞),故无上(下)界点列有非正常上(下)极限+∞(-∞),
对非正常上(或下)极限,定理7.5-7.9也成立(其中定理7.7需要修改)













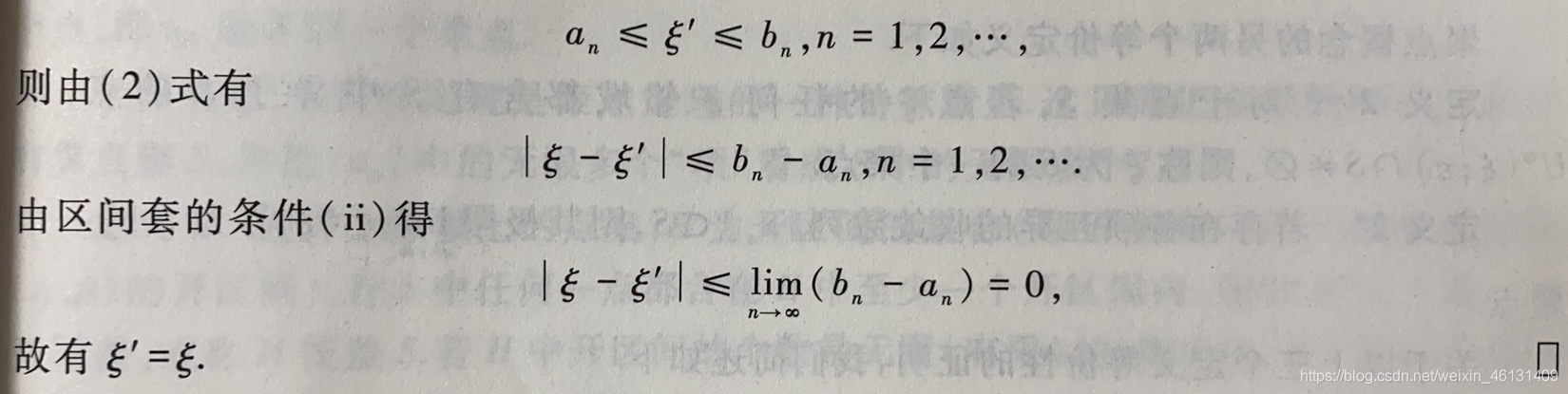














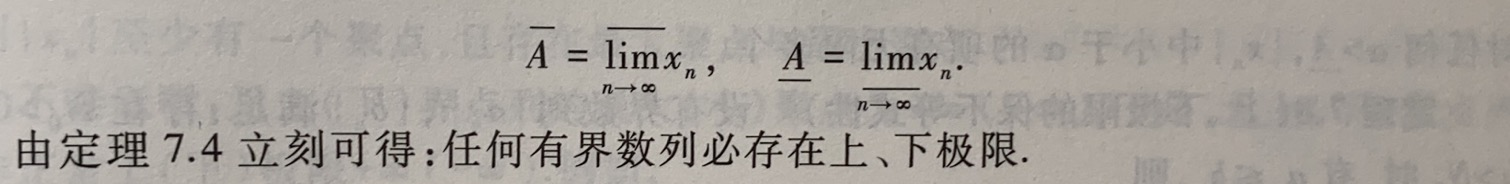
















 335
335











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








