高等代数 矩阵的相抵和相似(第5章)2 相似,特征值与特征向量,对角化

一.矩阵的相似(5.4)

1.相似矩阵
(1)概念:

(2)性质:

性质1:如果$B_1=P^{-1}{A}_{1}P,B_2=P^{-1}{A}_{2}P$,那么$$\begin{gathered} B_1+B_2=P^{-1}(A_1+A_2)P \\ {B}_1{B}_2=P^{-1}(A_1{A}_2)P \\ {B}_1^m=P^{-1}{A}_1^{m}P \end{gathered}$$其中$m$是正整数

性质2:若$A\sim B$,则$$|B|=|A|$$

性质3:相似的矩阵或者都可逆,或者都不可逆;当它们可逆时,它们的逆矩阵也相似

性质4:若$A\sim B$,则$$rank(B)=rank(A)$$

2.迹
(1)概念:

(2)性质:

性质5:矩阵的迹具有下列性质:$$\begin{gathered} tr(A+B)tr(A)+tr(B)(3) \\ tr(kA)=k\cdot tr(A)(4) \\ tr(AB)=tr(BA)(5) \end{gathered}$$

性质6:若$A\sim B$,则$$tr(A)=tr(B)$$

3.相似不变量:

4.矩阵可对角化:

定理1:数域$K$上的$n$级矩阵$A$可对角化的充要条件是:$K^n$中有$n$个线性无关的列向量${\alpha }_1,{\alpha }_2...{\alpha }_n$,以及$K$中有$n$个数${\lambda }_1,{\lambda }_2...{\lambda }_n$(这$n$个数中可能有些是相等的),使得$$A{\alpha }_i={\lambda }_i{\alpha }_i(i=1,2...n)(6)$$这时,令$P=({\alpha }_1,{\alpha }_2...{\alpha }_n)$,则 P − 1 A P = d i a g { λ 1 , λ 2 . . . λ n } P^{-1}AP=diag\{λ_1,λ_2...λ_n\} P−1AP=diag{λ1​,λ2​...λn​}

二.矩阵的特征值与特征向量(5.5)

1.概念:

2.存在性与求法
(1)特征矩阵与特征多项式:

将$\lambda I-A=\left[\begin{array}{cccc}\lambda -a_{11}& -a_{12}& ...& -a_{1n}\\ -a_{21}& \lambda -a_{22}& ...& -a_{2n}\\ ...& ...& ...& ...\\ -a_{n1}& -a_{n2}& ...& \lambda -a_{nn}\end{array}\right]$称为矩阵$A$的特征矩阵
①由于$\lambda -a_{ii}\notin F(i=1,2...n)$,从而$\lambda I-A$不是域$F$上的矩阵;由于$\lambda -a_{ii}\in F[\lambda ](i=1,2...n)$,从而$\lambda I-A$是域$F$上一元多项式环$F[\lambda ]$上的矩阵
②对环$F[\lambda ]$上的矩阵,也可以定义加法/矩阵乘法/纯量乘法/行列式等概念,且这些概念和域$F$上矩阵的相应概念相同(参见 高等代数.多项式环5.二.4.(1) 部分)

命题1:设$A$是数域$K$上的$n$级矩阵,则$A$的特征多项式$|\lambda I-A|$是1个$n$次多项式,${\lambda }^n$的系数是1,${\lambda }^{n-1}$的系数等于$-tr(A)$,常数项为$(-1{)}^n|A|,{\lambda }^{n-k}$的系数为$A$的所有$k$阶主子式的和乘以$(-1{)}^k(1\le k<n)$

(2)特征值与特征向量的求法:

定理2:设$A$是数域$K$上的$n$级矩阵,则:
$(1){\lambda }_0$是$A$的1个特征值当且仅当${\lambda }_0$是$A$的特征多项式$|\lambda I-A|$在$K$中的1个根
$(2)\alpha$是$A$的属于特征值${\lambda }_0$的1个特征向量当且仅当$\alpha$是齐次线性方程组$({\lambda }_{0}I-A)x=0$的1个非零解

(3)求矩阵的所有特征值与特征向量的一般步骤:

(4)特征子空间:

3.相似矩阵的性质(续):

性质1:相似的矩阵具有相等的特征多项式

性质2:相似的矩阵具有相同的特征值(包括重数)

由性质1,性质2可以看出,矩阵的特征多项式和特征值是相似不变量

另外,相似矩阵的特征向量不一定相同,实际上,通常不同

4.几何重数与代数重数
(1)概念:

(2)二者的关系:

命题2:设${\lambda }_1$是数域$K$上$n$级矩阵$A$的1个特征值,则${\lambda }_1$的几何重数不超过其代数重数

三.矩阵可对角化的条件(5.6)
1.矩阵可对角化的条件:

定理3(即 一.4 部分的定理1):数域$K$上的$n$级矩阵$A$可对角化的充要条件是:$A$有$n$个线性无关的特征向量${\alpha }_1,{\alpha }_2...{\alpha }_n$,此时令$$P=({\alpha }_1,{\alpha }_2...{\alpha }_n)$$则 P − 1 A P = d i a g { λ 1 , λ 2 . . . λ n } P^{-1}AP=diag\{λ_1,λ_2...λ_n\} P−1AP=diag{λ1​,λ2​...λn​}其中${\lambda }_i(i=1,2...n)$是${\alpha }_i$所属的特征值,上述对角矩阵称为$A$的相似标准型,除了主对角线上元素的排列次序外,$A$的相似标准型是唯一的

定理4:数域$K$上的$n$级矩阵$A$可对角化的充要条件是:$A$的属于不同特征值的特征子空间的维数之和等于$n$


推论1:数域$K$上的$n$级矩阵$A$如果有$n$个不同的特征值,那么$A$可对角化

定理5:数域$K$上的$n$级矩阵$A$可对角化的充要条件是:$A$的特征多项式的全部复根都属于$K$,并且$A$的每个特征值的几何重数都等于其代数重数

2.属于不同特征值的特征向量线性无关:

定理6:设${\lambda }_1,{\lambda }_2$是数域$K$上$n$级矩阵$A$的不同的特征值,${\alpha }_1,{\alpha }_2...{\alpha }_s$与${\beta }_1,{\beta }_2...{\beta }_r$分别是$A$的属于${\lambda }_1,{\lambda }_2$的线性无关的特征向量,则${\alpha }_1,{\alpha }_2...{\alpha }_s,{\beta }_1,{\beta }_2...{\beta }_r$线性无关

定理7:设${\lambda }_1,{\lambda }_2...{\lambda }_m$是数域$K$上$n$级矩阵$A$的不同的特征值,${\alpha }_{j1},{\alpha }_{j2}...{\alpha }_{j{r}_j}$是$A$的属于${\lambda }_j(j=1,2...m)$的线性无关的特征向量,则向量组${\alpha }_{11}...{\alpha }_{1r_1}...{\alpha }_{m1}...{\alpha }_{m{r}_m}$线性无关

推论1:$n$级矩阵$A$的属于不同特征值的特征向量是线性无关的

四.实对称矩阵的对角化(5.7)


1.相关概念
(1)实对称矩阵:

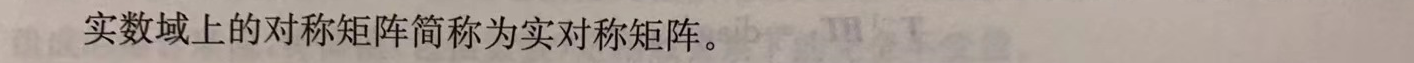
(2)正交相似:

2.实对称矩阵的特征值与特征向量:

定理8:实对称矩阵的特征多项式的每个复根都是实数,从而它们都是特征值

定理9:实对称矩阵$A$的属于不同特征值的特征向量是正交的

3.实对称矩阵的对角化
(1)实对称矩阵必可对角化:

定理10:实对称矩阵一定正交相似于对角矩阵


该定理表明:实对称矩阵一定可对角化

(2)实对称矩阵对角化的步骤:

(3)相关结论:

命题3:如果$n$级实矩阵$A$正交相似于1个对角矩阵$D$,那么$A$一定是对称矩阵

命题4:2个$n$级实对称矩阵正交相似的充要条件是它们相似