一.有理标准形(9.9)

1.零化多项式

(1)定义:

(2)判定:
命题1:设 C C C是域 F F F上有限维线性空间 W W W上的线性变换.对 0 ≠ α ∈ W , g ( λ ) 0≠α∈W,g(λ) 0=α∈W,g(λ)是 α α α的零化多项式当且仅当 α α α的最小多项式 m α ( λ ) ∣ g ( λ ) m_α(λ)\,|\,g(λ) mα(λ)∣g(λ)
2.循环子空间与友矩阵
命题2:设 C C C是域 F F F上有限维线性空间 W W W上的线性变换.对 0 ≠ α ∈ W 0≠α∈W 0=α∈W,设 α α α的最小多项式 m α ( λ ) m_α(λ) mα(λ)为 m α ( λ ) = λ t + d t − 1 λ t − 1 + . . . + d 1 λ + d 0 ( 5 ) m_α(λ)=λ^t+d_{t-1}λ^{t-1}+...+d_1λ+d_0\qquad(5) mα(λ)=λt+dt−1λt−1+...+d1λ+d0(5)则 α , C α . . . C t − 1 α α,Cα...C^{t-1}α α,Cα...Ct−1α线性无关,且 C t α C^tα Ctα可由 α , C α . . . C t − 1 α α,Cα...C^{t-1}α α,Cα...Ct−1α线性表出
受该命题启发,引进循环子空间的概念
(1)定义:

(2)性质:
(命题2的)推论1:设 C C C是域 F F F上有限维线性空间 W W W上的线性变换.对 0 ≠ α ∈ W 0≠α∈W 0=α∈W,设 α α α的最小多项式 m α ( λ ) m_α(λ) mα(λ)为 m α ( λ ) = λ t + d t − 1 λ t − 1 + . . . + d 1 λ + d 0 ( 10 ) m_α(λ)=λ^t+d_{t-1}λ^{t-1}+...+d_1λ+d_0\qquad(10) mα(λ)=λt+dt−1λt−1+...+d1λ+d0(10)则 < α , C α . . . C t − 1 α > <α,Cα...C^{t-1}α> <α,Cα...Ct−1α>是 t t t维 C − C- C−循环子空间, C C C在该子空间上的限制在基 α , C α . . . C t − 1 α α,Cα...C^{t-1}α α,Cα...Ct−1α下的矩阵是 α α α的最小多项式 m α ( λ ) m_α(λ) mα(λ)的友矩阵, C ∣ < α , C α . . . C t − 1 α > C\,|\,<α,Cα...C^{t-1}α> C∣<α,Cα...Ct−1α>的特征多项式和最小多项式都等于 m α ( λ ) m_α(λ) mα(λ)
引理:设 C C C是域 F F F上有限维线性空间 W W W上的线性变换.对 0 ≠ α ∈ W 0≠α∈W 0=α∈W如果 α α α的最小多项式 m α ( λ ) = p h ( λ ) m_α(λ)=p^h(λ) mα(λ)=ph(λ),其中 p ( λ ) p(λ) p(λ)是域 F F F上次数 r > 1 r>1 r>1的不可约多项式,那么 < α , C α . . . C t − 1 α > <α,Cα...C^{t-1}α> <α,Cα...Ct−1α>不能分解成 C ∣ < α , C α . . . C t − 1 α > C\,|\,<α,Cα...C^{t-1}α> C∣<α,Cα...Ct−1α>的非平凡不变子空间的直和,其中 t = deg m α ( λ ) = h r t=\deg{m_α}(λ)=hr t=degmα(λ)=hr
(命题2的)推论2:设 C C C是域 F F F上有限维线性空间 W W W上的线性变换.对 0 ≠ α ∈ W 0≠α∈W 0=α∈W如果 α α α的最小多项式 m α ( λ ) = p h ( λ ) m_α(λ)=p^h(λ) mα(λ)=ph(λ),其中 p ( λ ) p(λ) p(λ)是域 F F F上次数 r > 1 r>1 r>1的不可约多项式,那么 m α ( λ ) m_α(λ) mα(λ)的友矩阵不能表示成分块对角矩阵
3.有理标准形
命题3:设 C ℂ C是域 F F F上有限维线性空间 W W W上的线性变换.对 ∀ 0 ≠ α ∈ W \forall0≠α∈W ∀0=α∈W,如果 α α α的最小多项式 m α ( λ ) = p h ( λ ) m_α(λ)=p^h(λ) mα(λ)=ph(λ),其中 p ( λ ) p(λ) p(λ)是域 F F F上次数 r > 1 r>1 r>1的不可约多项式,那么 m α ( λ ) m_α(λ) mα(λ)的友矩阵不能表示成分块对角矩阵
(1)单个不可约因式的情形:
定理1:设 C ℂ C是域 F F F上 m m m维线性空间 W W W上的线性变换.如果 C ℂ C的最小多项式 m ( λ ) = p ( λ ) m(λ)=p(λ) m(λ)=p(λ),其中 p ( λ ) p(λ) p(λ)是域 F F F上次数 r > 1 r>1 r>1的不可约多项式,那么 W W W能分解成 m r \frac{m}{r} rm个 r r r维 C − ℂ- C−循环子空间的直和
(定理1的)推论1:设 C ℂ C是域 F F F上 m m m维线性空间 W W W上的线性变换.如果 C ℂ C的最小多项式 m ( λ ) = p ( λ ) m(λ)=p(λ) m(λ)=p(λ),其中 p ( λ ) p(λ) p(λ)是域 F F F上次数 r > 1 r>1 r>1的不可约多项式,那么 W W W中存在1个基使得 C ℂ C在此基下的矩阵 C C C是由 m r \frac{m}{r} rm个 p ( λ ) p(λ) p(λ)的友矩阵组成的分块对角矩阵,称其为 C ℂ C的有理标准形. C ℂ C的有理标准形是唯一的,并且是 C ℂ C的最简单形式的矩阵表示
(2)多个相同的不可约因式的情形:
命题4:设 C ℂ C是域 F F F上 m m m维线性空间 W W W上的线性变换.如果 C ℂ C的最小多项式 m ( λ ) = p l ( λ ) m(λ)=p^l(λ) m(λ)=pl(λ),其中 l > 1 , p ( λ ) l>1,p(λ) l>1,p(λ)是域 F F F上次数 r > 1 r>1 r>1的不可约多项式,那么对 ∀ 0 ≠ α ∈ W , α \forall0≠α∈W,α ∀0=α∈W,α的最小多项式 m α ( λ ) = p h ( λ ) ( l ≥ h ∈ Z + ) m_α(λ)=p^h(λ)\,(l≥h∈Z^+) mα(λ)=ph(λ)(l≥h∈Z+);并且 p ( C ) α p(ℂ)α p(C)α的最小多项式 m p ( C ) α ( λ ) = p h − 1 ( λ ) m_{p(ℂ)α}(λ)=p^{h-1}(λ) mp(C)α(λ)=ph−1(λ).把 α α α生成的 h r hr hr维 C − C- C−循环子空间记作 W h r ( α ) W_{hr}(α) Whr(α),则 p ( C ) α p(ℂ)α p(C)α生成的 ( h − 1 ) r (h-1)r (h−1)r维 C − ℂ- C−循环子空间等于 p ( C ) W h r ( α ) p(ℂ)W_{hr}(α) p(C)Whr(α)
定理2:设 C ℂ C是域 F F F上 m m m维线性空间 W W W上的线性变换.如果 C ℂ C的最小多项式 m ( λ ) = p l ( λ ) m(λ)=p^l(λ) m(λ)=pl(λ),其中 l > 1 , p ( λ ) l>1,p(λ) l>1,p(λ)是域 F F F上次数 r > 1 r>1 r>1的不可约多项式,那么 W W W能分解成 dim W 0 r \frac{\dim_{W_0}}{r} rdimW0个 C − ℂ- C−循环子空间的直和,其中 W 0 W_0 W0是 p ( C ) p(ℂ) p(C)的属于特征值0的特征子空间,从而 W W W中存在1个基,使得 C ℂ C在此基下的矩阵 C = d i a g { C 1 , C 2 . . . C v } ( v = dim W 0 r ) C=diag\{C_1,C_2...C_v\}\,(v=\frac{\dim{W_0}}{r}) C=diag{C1,C2...Cv}(v=rdimW0),其中 C i C_i Ci是 p h i ( λ ) ( 1 ≤ h i ≤ l , i = 1 , 2... v ) p^{h_i}(λ)\,(1≤h_i≤l,i=1,2...v) phi(λ)(1≤hi≤l,i=1,2...v)的友矩阵,称为1个有理块; C C C中有理块的总数 v = m − r a n k [ p ( C ) ] r v=\frac{m-rank[p(ℂ)]}{r} v=rm−rank[p(C)];对于 1 ≤ h ≤ l , C 1≤h≤l,C 1≤h≤l,C中 h r hr hr级有理块的个数为 N ( h r ) = r a n d [ p h − 1 ( C ) ] + r a n d [ p h + 1 ( C ) ] − 2 r a n d [ p h ( C ) ] r N(hr)=\frac{rand[p^{h-1}(ℂ)]+rand[p^{h+1}(ℂ)]-2rand[p^h(ℂ)]}{r} N(hr)=rrand[ph−1(C)]+rand[ph+1(C)]−2rand[ph(C)] C C C称为 C ℂ C的1个有理标准形.除有理块的排列次序外, C ℂ C的有理标准形 C C C是唯一的,并且 C C C是 C ℂ C的最简单形式的矩阵表示
(定理2的)推论1:设 C ℂ C是域 F F F上 m m m维线性空间 W W W上的线性变换.如果 C ℂ C的最小多项式 m ( λ ) = p l ( λ ) m(λ)=p^l(λ) m(λ)=pl(λ),其中 l > 1 , p ( λ ) l>1,p(λ) l>1,p(λ)是域 F F F上次数 r > 1 r>1 r>1的不可约多项式,那么 C ℂ C的有理标准形 C C C中一定有 l r lr lr级有理块
(3)多个不同的不可约因式的情形:
定理3:设 Ꭿ Ꭿ Ꭿ是域 F F F上 n n n维线性空间 V V V上的线性变换,如果 Ꭿ Ꭿ Ꭿ的最小多项式 m ( λ ) m(λ) m(λ)在 F [ λ ] F[λ] F[λ]中的标准分解式为 m ( λ ) = p 1 l 1 ( λ ) p 2 l 2 ( λ ) . . . p s l s ( λ ) m(λ)=p_1^{l_1}(λ)p_2^{l_2}(λ)...p_s^{l_s}(λ) m(λ)=p1l1(λ)p2l2(λ)...psls(λ)其中 deg p j ( λ ) = r j ( j = 1 , 2... s ) \deg{p_j(λ)}=r_j\,(j=1,2...s) degpj(λ)=rj(j=1,2...s),那么 V V V中存在1个基,使得 Ꭿ Ꭿ Ꭿ在此基下的矩阵 C C C是由有理块组成的分块对角矩阵; C C C中对应于 p j l j ( λ ) p_j^{l_j}(λ) pjlj(λ)的有理块的总数为 N j = n − r a n k [ p j ( Ꭿ ) ] r j N_j=\frac{n-rank[p_j(Ꭿ)]}{r_j} Nj=rjn−rank[pj(Ꭿ)]其中 h r j hr_j hrj级有理块的个数为 N j ( h r j ) = r a n k [ p j h − 1 ( Ꭿ ) ] + r a n k [ p j h + 1 ( Ꭿ ) ] − 2 r a n k [ p j h ( Ꭿ ) ] r j N_j(hr_j)=\frac{rank[p_j^{h-1}(Ꭿ)]+rank[p_j^{h+1}(Ꭿ)]-2rank[p_j^h(Ꭿ)]}{r_j} Nj(hrj)=rjrank[pjh−1(Ꭿ)]+rank[pjh+1(Ꭿ)]−2rank[pjh(Ꭿ)]其中 1 ≤ h ≤ l j ( j = 1 , 2... s ) 1≤h≤l_j\,(j=1,2...s) 1≤h≤lj(j=1,2...s). C C C称为 Ꭿ Ꭿ Ꭿ的有理标准形.除有理块的排列次序外, Ꭿ Ꭿ Ꭿ的有理标准形 C C C是唯一的
(定理3的)推论1:设 A A A是域 F F F上的 n n n级矩阵,如果 A A A的最小多项式 m ( λ ) m(λ) m(λ)在 F [ λ ] F[λ] F[λ]中的标准分解式为 m ( λ ) = p 1 l 1 ( λ ) p 2 l 2 ( λ ) . . . p s l s ( λ ) m(λ)=p_1^{l_1}(λ)p_2^{l_2}(λ)...p_s^{l_s}(λ) m(λ)=p1l1(λ)p2l2(λ)...psls(λ)其中 deg p j ( λ ) = r j ( j = 1 , 2... s ) \deg{p_j(λ)}=r_j\,(j=1,2...s) degpj(λ)=rj(j=1,2...s),那么 A A A相似于1个由有理块组成的分块对角矩阵 C , C C,C C,C中对应于 p j l j ( λ ) p_j^{l_j}(λ) pjlj(λ)的有理块的总数为 N j = n − r a n k [ p j ( A ) ] r j N_j=\frac{n-rank[p_j(A)]}{r_j} Nj=rjn−rank[pj(A)]其中 h r j hr_j hrj级有理块的个数为 N j ( h r j ) N_j(hr_j) Nj(hrj)为 N j ( h r j ) = r a n k [ p j h − 1 ( A ) ] + r a n k [ p j h + 1 ( A ) ] − 2 r a n k [ p j h ( A ) ] r j N_j(hr_j)=\frac{rank[p_j^{h-1}(A)]+rank[p_j^{h+1}(A)]-2rank[p_j^h(A)]}{r_j} Nj(hrj)=rjrank[pjh−1(A)]+rank[pjh+1(A)]−2rank[pjh(A)]其中 1 ≤ h ≤ l j ( j = 1 , 2... s ) 1≤h≤l_j\,(j=1,2...s) 1≤h≤lj(j=1,2...s). C C C称为 A A A的有理标准形.除有理块的排列次序外, A A A的有理标准形 C C C是唯一的
4.广义有理标准形
(1)任意域上的情形:

定理4:设 Ꭿ Ꭿ Ꭿ是域 F F F上 n n n维线性空间 V V V上的线性变换,如果 Ꭿ Ꭿ Ꭿ的最小多项式 m ( λ ) m(λ) m(λ)在 F [ λ ] F[λ] F[λ]中的标准分解式为 m ( λ ) = ( λ − λ 1 ) l 1 . . . ( λ − λ s ) l s p 1 k 1 ( λ ) p 2 k 2 ( λ ) . . . p v k v ( λ ) m(λ)=(λ-λ_1)^{l_1}...(λ-λ_s)^{l_s}p_1^{k_1}(λ)p_2^{k_2}(λ)...p_v^{k_v}(λ) m(λ)=(λ−λ1)l1...(λ−λs)lsp1k1(λ)p2k2(λ)...pvkv(λ)其中 deg p j ( λ ) = r j > 1 ( j = 1 , 2... v ) \deg{p_j(λ)}=r_j>1\,(j=1,2...v) degpj(λ)=rj>1(j=1,2...v),那么 V V V中存在1个基,使得 Ꭿ Ꭿ Ꭿ在此基下的矩阵 C C C是由约当块和有理块组成的分块对角矩阵. C C C中主对角元为 λ i λ_i λi的约当块总数 N ~ i = n − r a n k ( Ꭿ − λ i I ) \tilde{N}_i=n-rank(Ꭿ-λ_iℐ) N~i=n−rank(Ꭿ−λiI)其中 t t t级约当块的个数为 N ~ i ( t ) = r a n k ( Ꭿ − λ i I ) t − 1 + r a n k ( Ꭿ − λ i I ) t + 1 − 2 r a n k ( Ꭿ − λ i I ) t \tilde{N}_i(t)=rank(Ꭿ-λ_iℐ)^{t-1}+rank(Ꭿ-λ_iℐ)^{t+1}-2rank(Ꭿ-λ_iℐ)^t N~i(t)=rank(Ꭿ−λiI)t−1+rank(Ꭿ−λiI)t+1−2rank(Ꭿ−λiI)t其中 1 ≤ t ≤ l i ( i = 1 , 2... s ) ; C 1≤t≤l_i\,(i=1,2...s);C 1≤t≤li(i=1,2...s);C中对应于 p j k j ( λ ) p_j^{k_j}(λ) pjkj(λ)的有理块的总数为 N j = n − r a n k [ p j ( Ꭿ ) ] r j N_j=\frac{n-rank[p_j(Ꭿ)]}{r_j} Nj=rjn−rank[pj(Ꭿ)]其中 h r j hr_j hrj级有理块的个数为 N j ( h r j ) = r a n k [ p j h − 1 ( Ꭿ ) ] + r a n k [ p j h + 1 ( Ꭿ ) ] − 2 r a n k [ p j h ( Ꭿ ) ] r j N_j(hr_j)=\frac{rank[p_j^{h-1}(Ꭿ)]+rank[p_j^{h+1}(Ꭿ)]-2rank[p_j^h(Ꭿ)]}{r_j} Nj(hrj)=rjrank[pjh−1(Ꭿ)]+rank[pjh+1(Ꭿ)]−2rank[pjh(Ꭿ)]其中 1 ≤ h ≤ k j ( j = 1 , 2... v ) . C 1≤h≤k_j\,(j=1,2...v).C 1≤h≤kj(j=1,2...v).C称为 Ꭿ Ꭿ Ꭿ的广义有理标准形.除去约当块和有理块的排列次序外, Ꭿ Ꭿ Ꭿ的广义有理标准形是唯一的
(定理4的)推论1:设 A A A是域 F F F上的 n n n级矩阵,如果 A A A的最小多项式 m ( λ ) m(λ) m(λ)在 F [ λ ] F[λ] F[λ]中的标准分解式为 m ( λ ) = ( λ − λ 1 ) l 1 . . . ( λ − λ s ) l s p 1 k 1 ( λ ) p 2 k 2 ( λ ) . . . p v k v ( λ ) m(λ)=(λ-λ_1)^{l_1}...(λ-λ_s)^{l_s}p_1^{k_1}(λ)p_2^{k_2}(λ)...p_v^{k_v}(λ) m(λ)=(λ−λ1)l1...(λ−λs)lsp1k1(λ)p2k2(λ)...pvkv(λ)其中 deg p j ( λ ) = r j > 1 ( j = 1 , 2... v ) \deg{p_j(λ)}=r_j>1\,(j=1,2...v) degpj(λ)=rj>1(j=1,2...v),那么 A A A相似于1个由约当块和有理块组成的分块对角矩阵 C C C. C C C中主对角元为 λ i λ_i λi的约当块总数 N ~ i = n − r a n k ( A − λ i I ) \tilde{N}_i=n-rank(A-λ_iI) N~i=n−rank(A−λiI)其中 t t t级约当块的个数为 N ~ i ( t ) = r a n k ( A − λ i I ) t − 1 + r a n k ( A − λ i I ) t + 1 − 2 r a n k ( A − λ i I ) t \tilde{N}_i(t)=rank(A-λ_iI)^{t-1}+rank(A-λ_iI)^{t+1}-2rank(A-λ_iI)^t N~i(t)=rank(A−λiI)t−1+rank(A−λiI)t+1−2rank(A−λiI)t其中 1 ≤ t ≤ l i ( i = 1 , 2... s ) ; C 1≤t≤l_i\,(i=1,2...s);C 1≤t≤li(i=1,2...s);C中对应于 p j k j ( λ ) p_j^{k_j}(λ) pjkj(λ)的有理块的总数为 N j = n − r a n k [ p j ( A ) ] r j N_j=\frac{n-rank[p_j(A)]}{r_j} Nj=rjn−rank[pj(A)]其中 h r j hr_j hrj级有理块的个数为 N j ( h r j ) = r a n k [ p j h − 1 ( A ) ] + r a n k [ p j h + 1 ( A ) ] − 2 r a n k [ p j h ( A ) ] r j N_j(hr_j)=\frac{rank[p_j^{h-1}(A)]+rank[p_j^{h+1}(A)]-2rank[p_j^h(A)]}{r_j} Nj(hrj)=rjrank[pjh−1(A)]+rank[pjh+1(A)]−2rank[pjh(A)]其中 1 ≤ h ≤ k j ( j = 1 , 2... v ) . C 1≤h≤k_j\,(j=1,2...v).C 1≤h≤kj(j=1,2...v).C称为 A A A的广义有理标准形.除去约当块和有理块的排列次序外, A A A的广义有理标准形是唯一的
(2)实数域上的情形:
(定理4的)推论2:设 Ꭿ Ꭿ Ꭿ是实数域 R R R上 n n n维线性空间 V V V上的线性变换,如果 Ꭿ Ꭿ Ꭿ的最小多项式 m ( λ ) m(λ) m(λ)在 R [ λ ] R[λ] R[λ]中的标准分解式为 m ( λ ) = ( λ − λ 1 ) k 1 . . . ( λ − λ m ) k m ( λ 2 + p 1 λ + q 1 ) l 1 . . . ( λ 2 + p s λ + q s ) l s m(λ)=(λ-λ_1)^{k_1}...(λ-λ_m)^{k_m}(λ^2+p_1λ+q_1)^{l_1}...(λ^2+p_sλ+q_s)^{l_s} m(λ)=(λ−λ1)k1...(λ−λm)km(λ2+p1λ+q1)l1...(λ2+psλ+qs)ls那么 V V V中存在1个基,使得 Ꭿ Ꭿ Ꭿ在此基下的矩阵 C C C是由约当块和有理块组成的分块对角矩阵. C C C中主对角元为 λ i λ_i λi的约当块总数 N ~ i = n − r a n k ( Ꭿ − λ i I ) \tilde{N}_i=n-rank(Ꭿ-λ_iℐ) N~i=n−rank(Ꭿ−λiI)其中 t t t级约当块的个数为 N ~ i ( t ) = r a n k ( Ꭿ − λ i I ) t − 1 + r a n k ( Ꭿ − λ i I ) t + 1 − 2 r a n k ( Ꭿ − λ i I ) t \tilde{N}_i(t)=rank(Ꭿ-λ_iℐ)^{t-1}+rank(Ꭿ-λ_iℐ)^{t+1}-2rank(Ꭿ-λ_iℐ)^t N~i(t)=rank(Ꭿ−λiI)t−1+rank(Ꭿ−λiI)t+1−2rank(Ꭿ−λiI)t其中 1 ≤ t ≤ k i ( i = 1 , 2... m ) ; C 1≤t≤k_i\,(i=1,2...m);C 1≤t≤ki(i=1,2...m);C中对应于 λ 2 + p j λ + q j λ^2+p_jλ+q_j λ2+pjλ+qj的有理块的总数为 N j = n − r a n k [ Ꭿ 2 + p j Ꭿ + q j I ] 2 N_j=\frac{n-rank[Ꭿ^2+p_jᎯ+q_jℐ]}{2} Nj=2n−rank[Ꭿ2+pjᎯ+qjI]其中 2 h 2h 2h级有理块的个数为 N j ( 2 h ) = r a n k [ ( Ꭿ 2 + p j Ꭿ + q j I ) h − 1 ] + r a n k [ ( Ꭿ 2 + p j Ꭿ + q j I ) h + 1 ] − 2 r a n k [ ( Ꭿ 2 + p j Ꭿ + q j I ) h ] 2 N_j(2h)=\frac{rank[(Ꭿ^2+p_jᎯ+q_jℐ)^{h-1}]+rank[(Ꭿ^2+p_jᎯ+q_jℐ)^{h+1}]-2rank[(Ꭿ^2+p_jᎯ+q_jℐ)^h]}{2} Nj(2h)=2rank[(Ꭿ2+pjᎯ+qjI)h−1]+rank[(Ꭿ2+pjᎯ+qjI)h+1]−2rank[(Ꭿ2+pjᎯ+qjI)h]其中 1 ≤ h ≤ l j ( j = 1 , 2... s ) . C 1≤h≤l_j\,(j=1,2...s).C 1≤h≤lj(j=1,2...s).C称为 Ꭿ Ꭿ Ꭿ的广义有理标准形.除去约当块和有理块的排列次序外, Ꭿ Ꭿ Ꭿ的广义有理标准形是唯一的
(定理4的)推论3:设 A A A是实数域 R R R上的 n n n级矩阵,如果 A A A的最小多项式 m ( λ ) m(λ) m(λ)在 R [ λ ] R[λ] R[λ]中的标准分解式为 m ( λ ) = ( λ − λ 1 ) k 1 . . . ( λ − λ m ) k m ( λ 2 + p 1 λ + q 1 ) l 1 . . . ( λ 2 + p s λ + q s ) l s m(λ)=(λ-λ_1)^{k_1}...(λ-λ_m)^{k_m}(λ^2+p_1λ+q_1)^{l_1}...(λ^2+p_sλ+q_s)^{l_s} m(λ)=(λ−λ1)k1...(λ−λm)km(λ2+p1λ+q1)l1...(λ2+psλ+qs)ls那么 A A A相似于1个由约当块和有理块组成的分块对角矩阵 C C C. C C C中主对角元为 λ i λ_i λi的约当块总数 N ~ i = n − r a n k ( A − λ i I ) \tilde{N}_i=n-rank(A-λ_iI) N~i=n−rank(A−λiI)其中 t t t级约当块的个数为 N ~ i ( t ) = r a n k ( A − λ i I ) t − 1 + r a n k ( A − λ i I ) t + 1 − 2 r a n k ( A − λ i I ) t \tilde{N}_i(t)=rank(A-λ_iI)^{t-1}+rank(A-λ_iI)^{t+1}-2rank(A-λ_iI)^t N~i(t)=rank(A−λiI)t−1+rank(A−λiI)t+1−2rank(A−λiI)t其中 1 ≤ t ≤ K i ( i = 1 , 2... m ) ; C 1≤t≤K_i\,(i=1,2...m);C 1≤t≤Ki(i=1,2...m);C中对应于 λ 2 + p j λ + q j λ^2+p_jλ+q_j λ2+pjλ+qj的有理块的总数为 N j = n − r a n k ( A 2 + p j A + q j I ) 2 N_j=\frac{n-rank(A^2+p_jA+q_jI)}{2} Nj=2n−rank(A2+pjA+qjI)其中 h r j hr_j hrj级有理块的个数为 N j ( h r j ) = r a n k [ ( A 2 + p j A + q j I ) h − 1 ] + r a n k [ ( A 2 + p j A + q j I ) h + 1 ] − 2 r a n k [ ( A 2 + p j A + q j I ) h ] 2 N_j(hr_j)=\frac{rank[(A^2+p_jA+q_jI)^{h-1}]+rank[(A^2+p_jA+q_jI)^{h+1}]-2rank[(A^2+p_jA+q_jI)^h]}{2} Nj(hrj)=2rank[(A2+pjA+qjI)h−1]+rank[(A2+pjA+qjI)h+1]−2rank[(A2+pjA+qjI)h]其中 1 ≤ h ≤ l j ( j = 1 , 2... s ) . C 1≤h≤l_j\,(j=1,2...s).C 1≤h≤lj(j=1,2...s).C称为 A A A的广义有理标准形.除去约当块和有理块的排列次序外, A A A的广义有理标准形是唯一的
5.通过
λ
−
λ-
λ−矩阵求有理标准形
(1)
λ
−
λ-
λ−矩阵的初等因子与不变因子:

定理5:设 A ( λ ) A(λ) A(λ)是 F [ λ ] F[λ] F[λ]上的 n n n级满秩矩阵,通过初等变换把 A ( λ ) A(λ) A(λ)化成对角形,然后把主对角线上每个次数大于0的多项式分解成两两不等的不可约多项式的方幂的乘积,则所有这些不可约多项式的方幂(相同的按出现的次数计算)就是 A ( λ ) A(λ) A(λ)的初等因子
(2)矩阵与特征矩阵相抵的判定:
定理6: F [ λ ] F[λ] F[λ]上2个满秩的 n n n级矩阵相抵当且仅当它们有相同的初等因子
定理7:域 F F F上2个 n n n级矩阵的特征矩阵相抵的充要条件是它们有相同的不变因子或相同的初等因子
(3)矩阵的初等因子与不变因子:

(4)矩阵相似的判定:
定理8:域 F F F上2个 n n n级矩阵 A , B A,B A,B相似的充要条件是它们的特征矩阵 λ I − A , λ I − B λI-A,λI-B λI−A,λI−B相抵
定理9:域 F F F上2个 n n n级矩阵 A , B A,B A,B相似的充要条件是它们有相同的不变因子或相同的初等因子
(5)矩阵的有理标准形:

定理10:域 F F F上任一 n n n级矩阵 A A A都相似于1个由有理块组成的分块对角矩阵 C C C,除去其中有理块的排列次序外, C C C由 A A A唯一决定,称 C C C是 A A A的有理标准形
(定理10的)推论1:域 F F F上 n n n级矩阵 A A A的最小多项式 m ( λ ) m(λ) m(λ)等于 A A A的最后1个不变因子 d n ( λ ) d_n(λ) dn(λ)
(定理10的)推论2:设域 E ⊇ F E\supseteq F E⊇F,则域 F F F上2个 n n n级矩阵 A , B A,B A,B相似当且仅当把他们看成 E E E上的矩阵后相似
该推论说明域 F F F上 n n n级矩阵间的相似性不随域的扩大而改变
附录2.定理11的证明














 本文深入探讨了有理标准形的理论,包括零化多项式、循环子空间、友矩阵等概念,详细阐述了单个不可约因式、多个相同不可约因式及多个不同不可约因式情形下有理标准形的构造方法,并介绍了广义有理标准形在实数域上的应用。
本文深入探讨了有理标准形的理论,包括零化多项式、循环子空间、友矩阵等概念,详细阐述了单个不可约因式、多个相同不可约因式及多个不同不可约因式情形下有理标准形的构造方法,并介绍了广义有理标准形在实数域上的应用。








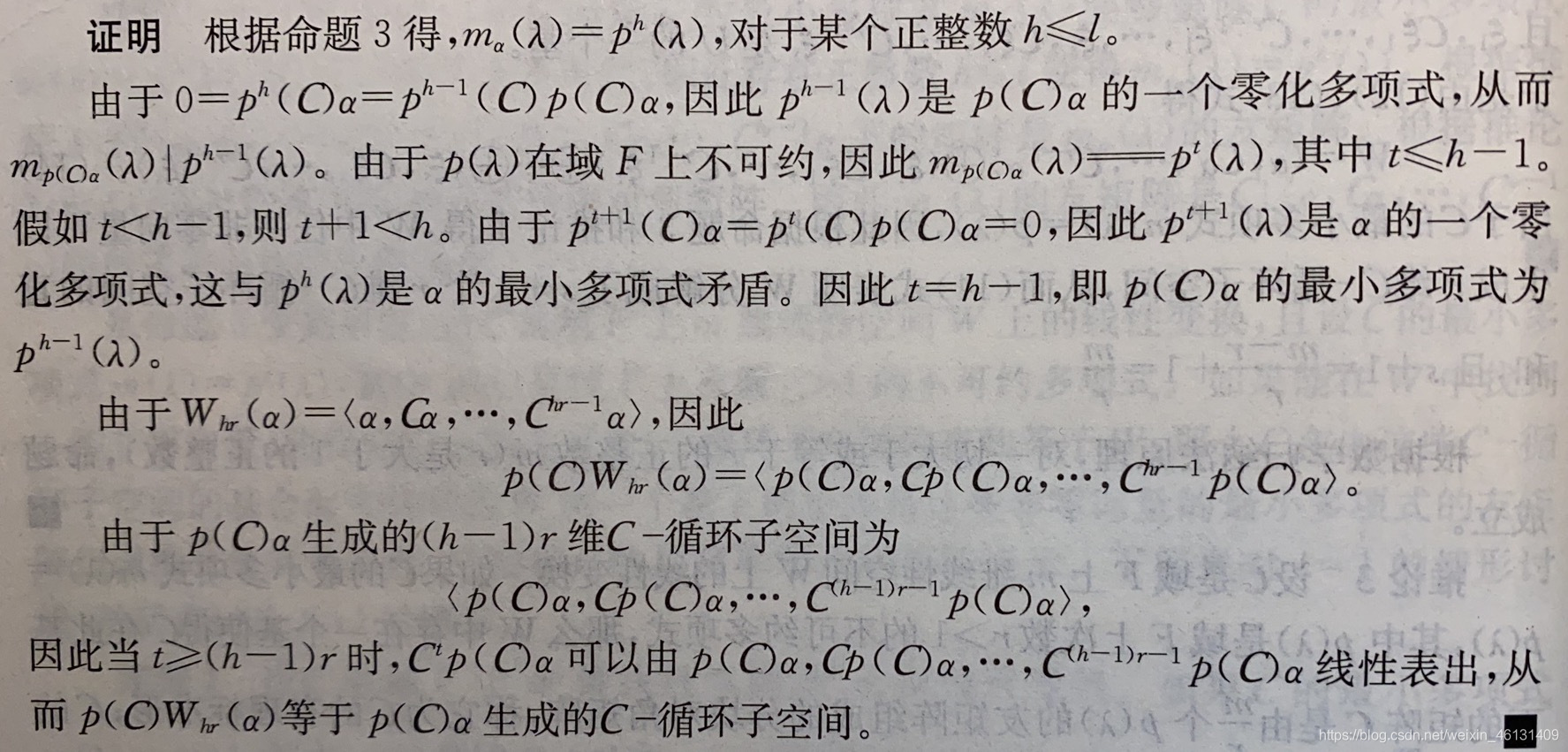

































 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








