机器学习（六）结果分析（过拟合、欠拟合）

一、模型评估常用方法

分类模型常用评估方法：

指标	描述
Accuracy	准确率
Precision	精准度/查准率
Recall	召回率/查全率
P-R曲线	查准率为纵轴，查全率为横轴，作图
F1	F1值
Confusion Matrix	混淆矩阵
ROC	ROC曲线
AUC	ROC曲线下的面积

回归模型常用评估方法：

指标	描述
Mean Square Error (MSE, RMSE)	平均方差
Absolute Error (MAE, RAE)	绝对误差
R-Squared	R平方值

二、误差（error）、偏差（bias）、方差（variance）的区别

1. 误差（error）

一般把模型预测结果与样本真实输出之间的差异称为误差，
error = bias + var + noise

2. 噪声（noise）

描述了在当前任务上任何学习算法所能达到的期望泛化误差的下界，刻画了学习问题本身的难度

3. 偏差（bias）

• 偏差衡量模型拟合训练数据的能力，反映在模型在样本上的输出与真实值之间的差距（不同于误差，误差是针对所有数据的，偏差只作用于样本数据），反应模型本身的精度

• 偏差越小，拟合能力越高，越接近真实数据；偏差越大，拟合能力越强

4. 方差（var）

• 方差公式：$S_N^2=\frac{1}{N}{\sum }_{i=1}^N(x_i-\bar{x}{)}^2$

• 方差描述的是预测结果偏离真实值的离散程度（距离度量）。方差越大，数据越分散，模型稳定性越差

• 方差越小，模型泛化能力越高；反之，泛化能力越低

5. 标准差

标准差公式为：$S_N=\sqrt{\frac{1}{N}{\sum }_{i=1}^N(x_i-\bar{x}{)}^2}$

样本标准差公式为：$S_N=\sqrt{\frac{1}{N-1}{\sum }_{i=1}^N(x_i-\bar{x}{)}^2}$

在样本数据大致符合正态分布的情况下，标准差具有方便估算的特性：68%的数据点落在平均值前后1个标准差的范围内、95%的数据点落在平均值前后2个标准差的范围内，而99%的数据点将会落在平均值前后3个标准差的范围内。也即 3$\sigma$ 的基本原理

5. 经验误差与泛化误差

经验误差（empirical error）：也叫训练误差（training error），模型在训练集上的误差。

泛化误差（generalization error）：模型在新样本集（测试集）上的误差称为“泛化误差”。

6. 偏差与方差图

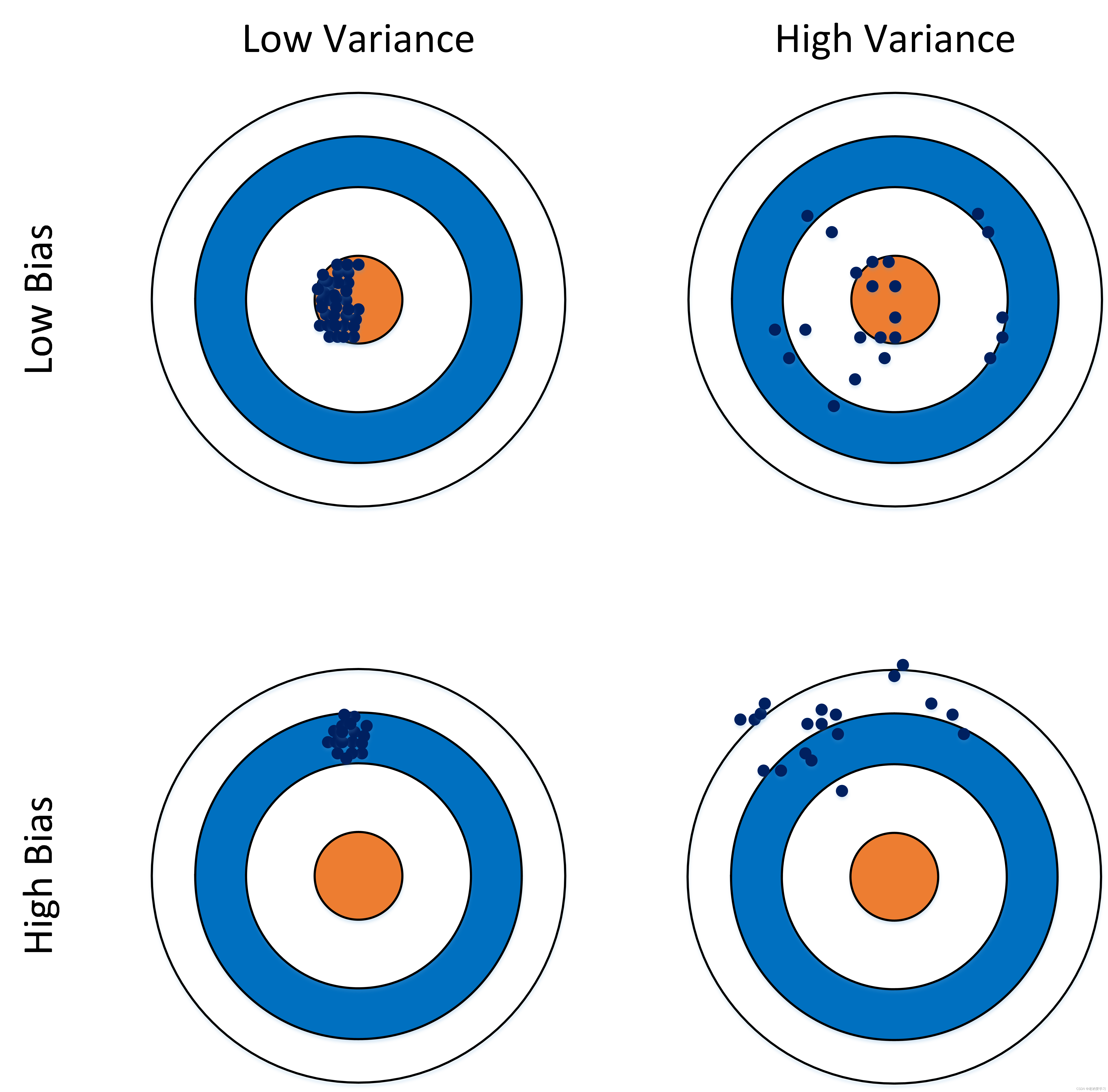
三、欠拟合、过拟合

1. 图示欠拟合和过拟合

根据不同的坐标方式，图解不同

1）横轴为训练样本数量，纵轴为误差

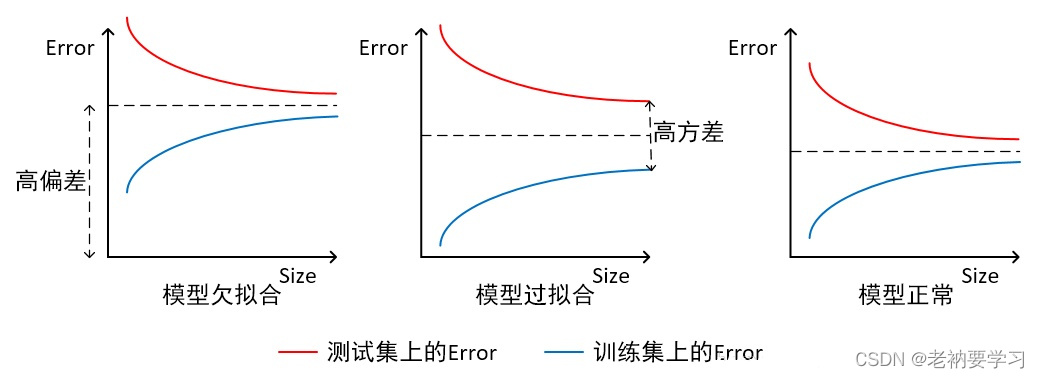
如上图所示，我们可以直观看出欠拟合和过拟合的区别：

• ​模型欠拟合：在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大；

• 模型过拟合：在训练集上具有较低的误差，在测试集上具有较高的误差，此时模型的方差较大。

• ​模型正常：在训练集以及测试集上，同时具有相对较低的偏差以及方差。

2）横轴为模型复杂程度，纵轴为误差

​

• 模型欠拟合：模型在点A处，在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大。
• 模型过拟合：模型在点C处，在训练集上具有较低的误差，在测试集上具有较高的误差，此时模型的方差较大。
• 模型正常：模型复杂程度控制在点B处为最优。

3）横轴正则项系数，纵轴误差

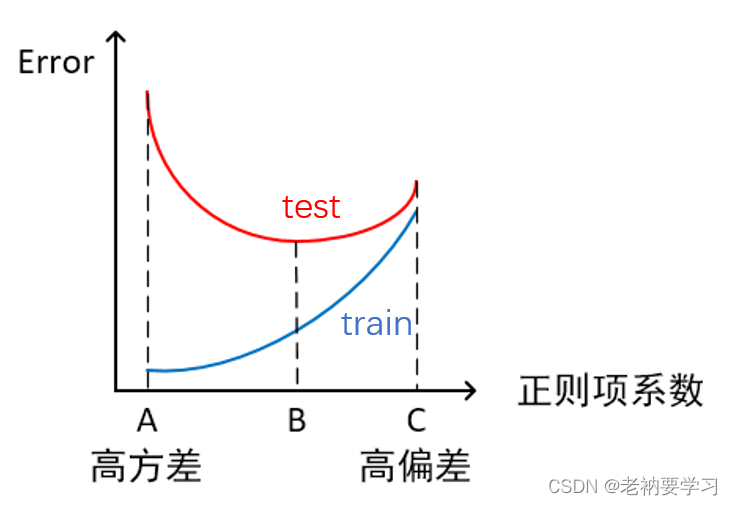
• 模型欠拟合：模型在点C处，在训练集以及测试集上同时具有较高的误差，此时模型的偏差较大。

• 模型过拟合：模型在点A处，在训练集上具有较低的误差，在测试集上具有较高的误差，此时模型的方差较大。 它通常发生在模型过于复杂的情况下，如参数过多等，会使得模型的预测性能变弱，并且增加数据的波动性。虽然模型在训练时的效果可以表现的很完美，基本上记住了数据的全部特点，但这种模型在未知数据的表现能力会大减折扣，因为简单的模型泛化能力通常都是很弱的。

• 模型正常：模型复杂程度控制在点B处为最优。

2. 如何解决过拟合与欠拟合

欠拟合出现的原因：欠缺特征、模型复杂度过低。
过拟合出现的原因：训练数据不足，模型复杂度过高。

1） 如何解决欠拟合

• 添加其他特征项。组合、泛化、相关性、上下文特征、平台特征等特征
• 添加多项式特征及增加模型复杂度，把一次模型增加到二次、三次等。
• 减小正则项系数，正则项是来防止过拟合的，但如果模型上出现了欠拟合，则需要减少正则化系数

2）如何解决过拟合！！！

• 增加训练样本数，重新清洗数据
• 降低模型复杂度
• 增大正则项系数
• 深度学习模型采用 dropout 方法
• early stopping
• 减小迭代次数
• 增大学习率
• 添加噪声数据
• 树模型可以进行剪枝
• 减少特征等

具体问题具体分析

四、类别不平衡问题

1. 问题描述

类别不平衡是指分类任务中，不同类别的训练样本数差距很大的情况

分类算法通常会假设不同类别的训练样本数目基本相同。如果不同类别的训练样本数差距很大，则会影响学习结果，测试结果变差。例如二分类问题中有 99 个正例，1 个反例，那么学习方法只需要返回正例就达到了 99% 的分类准确率，然而这样的模型没有价值。

2. 解决方法

1）扩大数据集

2）对大类数据欠采样

减少大类数据个数，使与小样本数目接近。但可能会丢失大样本重要信息
代表算法：EasyEnsemble。其思想是利用集成学习机制，将大类划分为若干集合提供不同的学习器使用。相当于对每个学习器都进行采样，但对于全局则不会丢失重要信息

3）对小类数据过采样

代表算法：SMOTE和ADASYN

SMOTE：通过对训练集中的小类别数据进行插值来产生额外的小类样本数
新的小类样本产生策略：对每个少数类样本 a ，在 a 的最近邻中随机选一个样本 b，然后在 a, b 之间的连线上随机选择一点作为新合成的随机样本

ADASYN：根据学习难度的不同，对不同的少数类别的样本使用加权分布，对于难以学习的少数类的样本，产生更多的综合数据。通过减少类不平衡引入的偏差和将分类决策边界自适应地转移到困难的样本的两种手段，改善了数据分布。

4）换评价指标，转化分析角度

将小类作为异常点，对其进行识别。

5）数据代价加权

对小类样本加权

6）将问题细化