一、河马优化算法
河马优化算法(Hippopotamus optimization algorithm,HO)由Amiri等人于2024年提出,该算法模拟了河马在河流或池塘中的位置更新、针对捕食者的防御策略以及规避方法。河马优化算法的灵感来自河马生活中观察到的三种突出行为模式。河马群由几只雌性河马、河马幼崽、多只成年雄性河马和一只占主导地位的雄性河马(牛群的领导者)组成.由于它们与生俱来的好奇心,幼崽和小河马经常表现出远离群体的倾向。因此,它们可能会变得孤立并成为捕食者的目标。



参考文献:
[1]Amiri, Mohammad Hussein, et al. “Hippopotamus Optimization Algorithm: a Novel Nature-Inspired Optimization Algorithm.” Scientific Reports, vol. 14, no. 1, Springer Science and Business Media LLC, Feb. 2024, doi:10.1038/s41598-024-54910-3.
二、23个函数介绍

参考文献:
[1] Yao X, Liu Y, Lin G M. Evolutionary programming made faster[J]. IEEE transactions on evolutionary computation, 1999, 3(2):82-102.
三、HO求解23个函数
3.1部分代码
close all ;
clear
clc
Npop=30;
Function_name='F1'; % Name of the test function that can be from F1 to F23 (
Tmax=300;
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_fit,Best_pos,Convergence_curve]=HO(Npop,Tmax,lb,ub,dim,fobj);
figure('Position',[100 100 660 290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
%Draw objective space
subplot(1,2,2);
semilogy(Convergence_curve,'Color','r','linewidth',3)
title('Search space')
xlabel('Iteration');
ylabel('Best score obtained so far');
axis tight
grid on
box on
legend('HO')
saveas(gca,[Function_name '.jpg']);
display(['The best solution is ', num2str(Best_pos)]);
display(['The best fitness value is ', num2str(Best_fit)]);
3.2部分结果
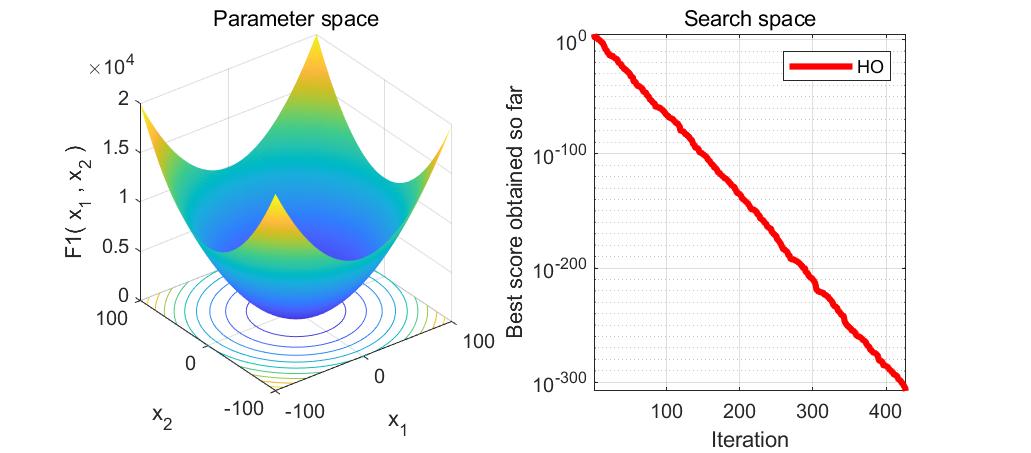
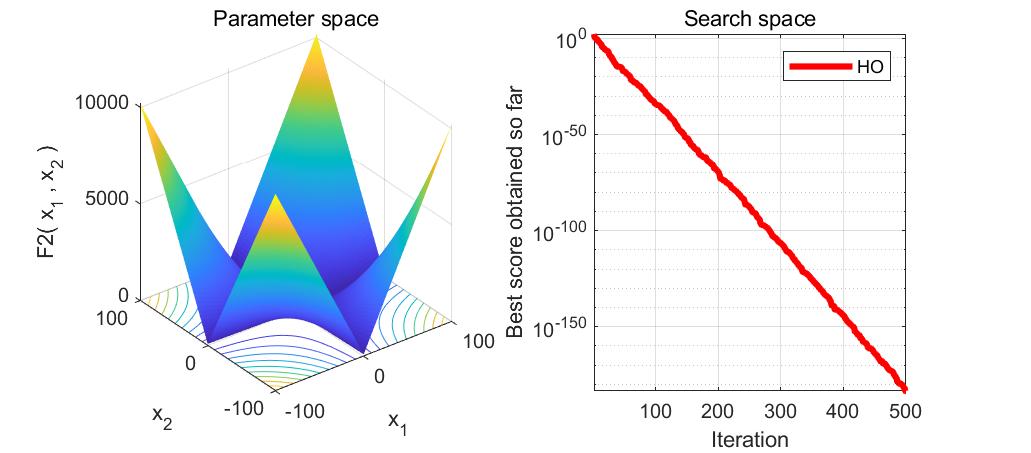
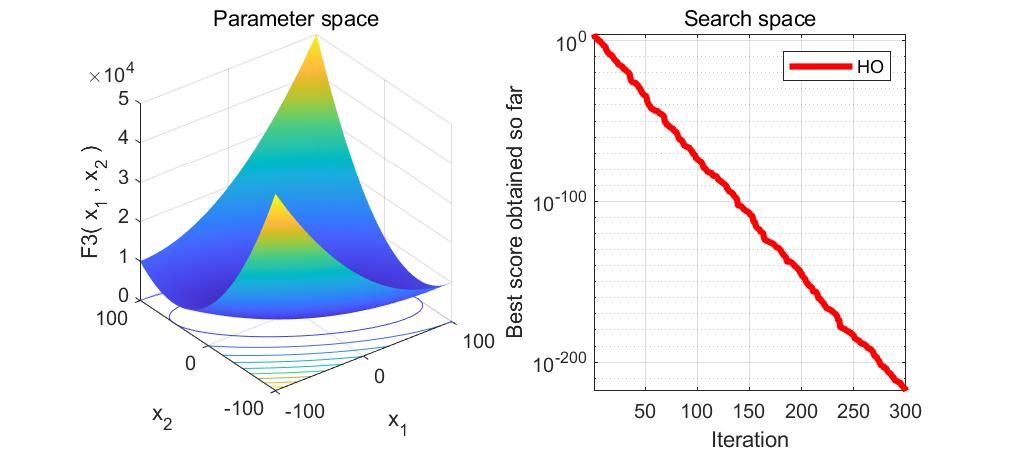
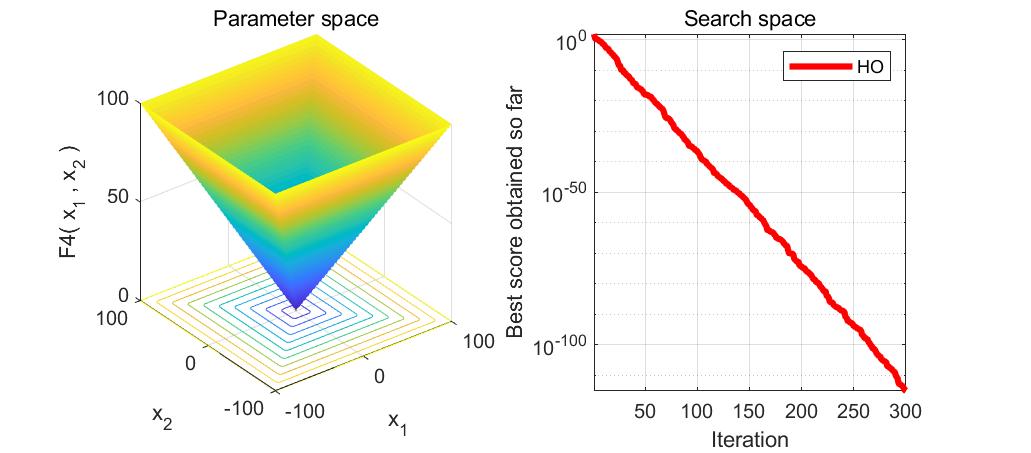
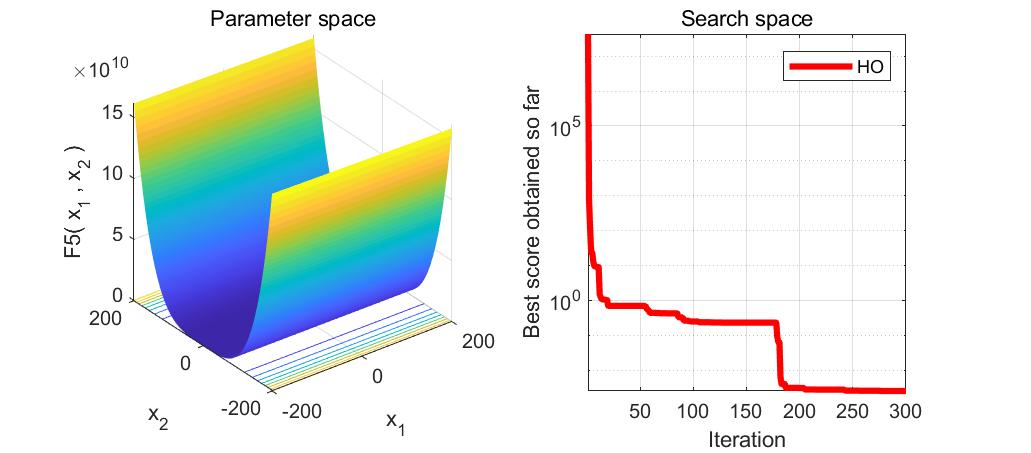
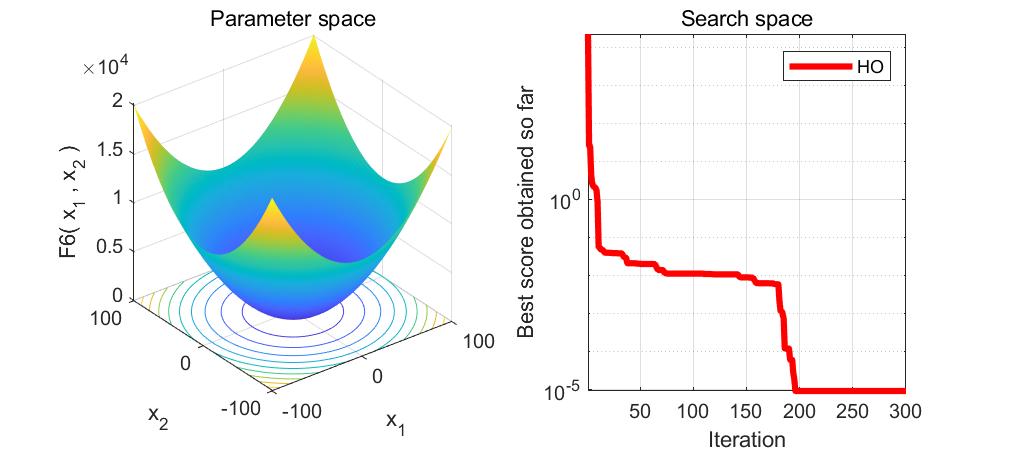
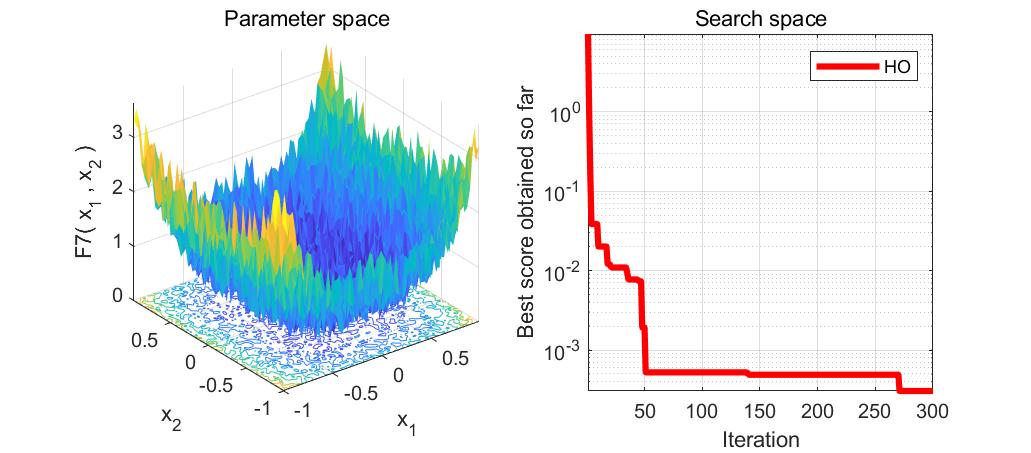
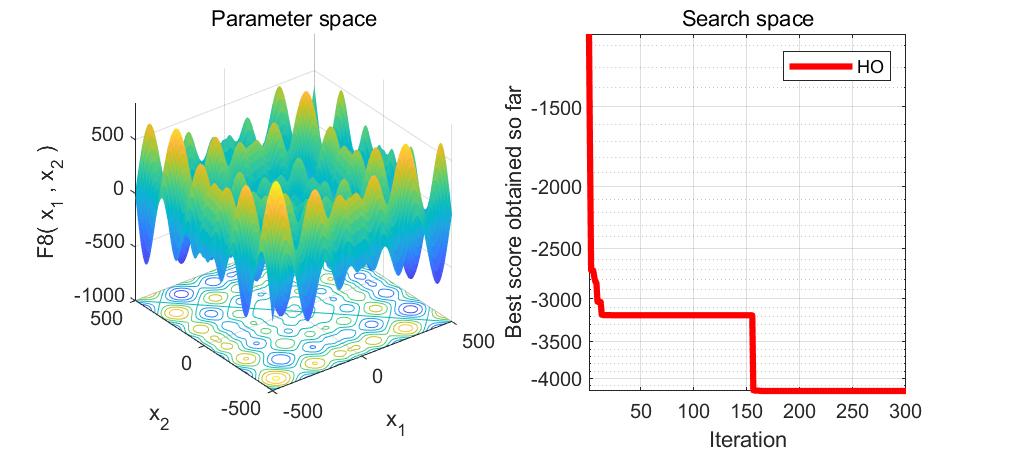










 本文介绍了河马优化算法(HippopotamusOptimizationAlgorithm,HO),一种受河马生活习性启发的优化算法,用于解决函数优化问题。通过MATLAB实现的代码展示了如何使用HO求解23个测试函数,包括搜索空间和目标空间的可视化。
本文介绍了河马优化算法(HippopotamusOptimizationAlgorithm,HO),一种受河马生活习性启发的优化算法,用于解决函数优化问题。通过MATLAB实现的代码展示了如何使用HO求解23个测试函数,包括搜索空间和目标空间的可视化。

















 2490
2490

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








