基于大型外卖配送平台场景下多骑手配送路径规划的离散浣熊优化算法（DCOA）研究，MATLAB代码

一、基于单仓库多旅行商问题的模型构建

骑手配送路径规划问题可类比为单仓库多旅行商问题。在这一情境下，配送站点作为唯一的仓库，是骑手的出发地与归宿。众多需要配送的订单地址则是分布在不同地理位置的客户节点。每个骑手从配送站点出发，负责若干订单的配送任务，遍历这些订单对应的客户节点后返回配送站点。目标是在满足订单配送时间要求、骑手工作时长限制、车辆载重（若有载货量限制情况）等约束条件下，为每个骑手规划出最短配送路径或总配送成本最低的路径，以实现配送效率的最大化。

二、骑手配送路径规划的特性

动态实时性：配送过程中，新订单随时可能涌入，订单状态也可能动态变化，如客户取消订单、修改收货地址或时间。同时，交通路况实时波动，高峰期拥堵、道路施工等情况频发。这就要求路径规划模型能够实时响应这些变化，动态调整骑手的配送路径和任务分配。例如，当某个区域突发交通事故导致道路拥堵时，系统需迅速为途经该区域的骑手重新规划路线，确保配送时效。
订单分配与路径规划紧密耦合：合理的订单分配是高效路径规划的前提，而优化的路径规划又能验证订单分配的合理性。若将距离过远、配送时间要求冲突的订单分配给同一骑手，会导致路径规划困难，增加配送成本和时间。反之，若路径规划不合理，即使订单分配看似合理，也难以实现高效配送。例如，将多个位于城市不同方向的加急订单分配给一位骑手，即便这些订单单独看都在骑手的配送能力范围内，但不合理的路线规划会使骑手疲于奔命，难以按时完成配送。
多约束条件：除了单仓库多旅行商问题中的一般约束，骑手配送还存在独特约束。骑手的工作时长受到劳动法规限制，以保障骑手的权益和工作效率；配送时间窗约束更为严格，尤其是外卖配送，食品的最佳食用时间限制决定了订单必须在极短的规定时间内送达；此外，部分配送场景可能涉及车辆的载重或容积限制，如配送大型物品时。

三、求解难点与挑战

NP - Hard 难题：骑手配送路径规划问题属于 NP - Hard 问题，随着订单数量的增加，可能的路径组合呈指数级增长。在实际配送中，一个繁忙的配送站点可能每天要处理成百上千个订单，要在如此庞大的解空间中找到全局最优解，计算量巨大，传统精确算法难以在有限时间内完成。
多目标平衡挑战：配送过程中需要兼顾多个目标，如最小化配送成本、最大化配送效率、提高客户满意度、均衡骑手工作量等。但这些目标之间存在冲突。例如，为降低成本可能选择较长但费用低的路线，这会延长配送时间，影响客户满意度；若追求最短配送时间，可能导致骑手工作量过大，影响服务质量和骑手积极性。如何在多个目标之间找到平衡，实现多目标协同优化，是路径规划面临的关键难题。
实时动态调整困境：由于配送过程中的动态不确定性因素众多，当出现交通拥堵、新订单插入等情况时，要实时调整路径规划，确保配送任务顺利完成，对算法的实时性和适应性提出了极高要求。传统算法难以快速响应并重新规划出合理路径，需要更智能、更高效的算法来应对。

四、常见求解算法与策略

精确算法的有限应用：在订单数量较少的小规模配送场景中，分支定界法、动态规划法等精确算法理论上可找到全局最优解。分支定界法通过将问题分解为子问题，界定子问题解空间，逐步缩小搜索范围；动态规划法则将问题分解为相互关联的子问题，通过求解子问题并保存结果来避免重复计算。但面对大规模订单配送问题，精确算法计算量过大，实际应用受限。
启发式算法的灵活运用：
节约算法：基于对配送距离的计算分析，比较不同订单组合的路径节约量，逐步合并订单，形成合理的配送路线。该算法简单直观、计算效率高，能快速生成较优解，但不一定能找到全局最优解，适用于对求解速度要求较高的即时配送场景。
扫描算法：以配送站点为中心，按一定角度对订单节点进行扫描，将相邻且符合约束条件的订单划分为一组，为每组规划配送路径。适用于订单分布较为均匀的区域，能有效减少计算量，但对订单分布的敏感度较高，当订单分布不均匀时，可能无法得到理想的路径规划结果。
智能优化算法的创新实践：
遗传算法：模拟生物遗传进化过程，将骑手的配送路径规划方案编码为染色体，通过选择、交叉、变异等遗传操作迭代优化种群，逐步搜索更优方案。具有较强全局搜索能力，但易出现早熟收敛问题，即过早地陷入局部最优解，无法找到全局最优解。
蚁群算法：模拟蚂蚁觅食释放信息素行为，蚂蚁依据信息素浓度选择下一个节点，信息素浓度高的路径被选概率大。随着时间推移，蚂蚁逐渐找到较优路径，适用于求解复杂的配送路径规划问题，但初期收敛速度慢，且容易受到参数设置的影响。
粒子群算法：把每个路径规划方案看作搜索空间中的粒子，粒子通过自身和群体经验更新位置和速度寻找最优解。收敛速度快、易于实现，但处理复杂问题时可能陷入局部最优，需要合理调整参数以平衡全局搜索和局部搜索能力。

五、实际应用案例分析

某大型外卖配送平台在某城市的配送业务中，起初由于订单分配和路径规划不合理，导致骑手配送效率低下，超时订单增多，客户投诉频繁。为解决这一问题，该平台引入基于遗传算法和蚁群算法的混合智能优化路径规划系统。通过对订单数据、交通路况数据、骑手位置数据等进行实时采集和分析，利用混合算法为骑手智能分配订单并规划最优配送路径。实施后，该城市的平均配送时长缩短了 15 分钟，超时订单率降低了 30%，客户满意度显著提升，同时骑手的工作效率提高，收入增加，实现了平台、骑手和客户的多方共赢。

六、离散浣熊优化算法

离散浣熊优化算法（Discrete Coati Optimization Algorithm，DCOA）是一种受浣熊群体行为启发而开发的用于解决离散优化问题的智能优化算法。浣熊在自然界中具有复杂而有趣的行为模式，它们以群体为单位进行活动，在寻找食物、选择栖息地等过程中展现出了一种高效的协作和探索能力。DCOA 就是模拟浣熊群体在搜索食物和适应环境过程中的行为特征，将其抽象为数学模型和算法步骤，用于解决骑手配送路径规划。

七、离散浣熊优化算法求解骑手配送路径规划

figure
hold on
new_pop = [];
for i = 1:m
    plot(city_coord(saleman_path{i},1),city_coord(saleman_path{i},2),'-o','MarkerSize',3,...
        'MarkerEdgeColor','b','LineWidth',2);
end
xlabel('X');
ylabel('Y');
title([num2str(m),'个旅行商的路径总长度：',num2str(path_sum)],'FontSize',12);
lgd = legend(salemans,'FontSize',12,'TextColor','black');
lgd.NumColumns = 2;

figure
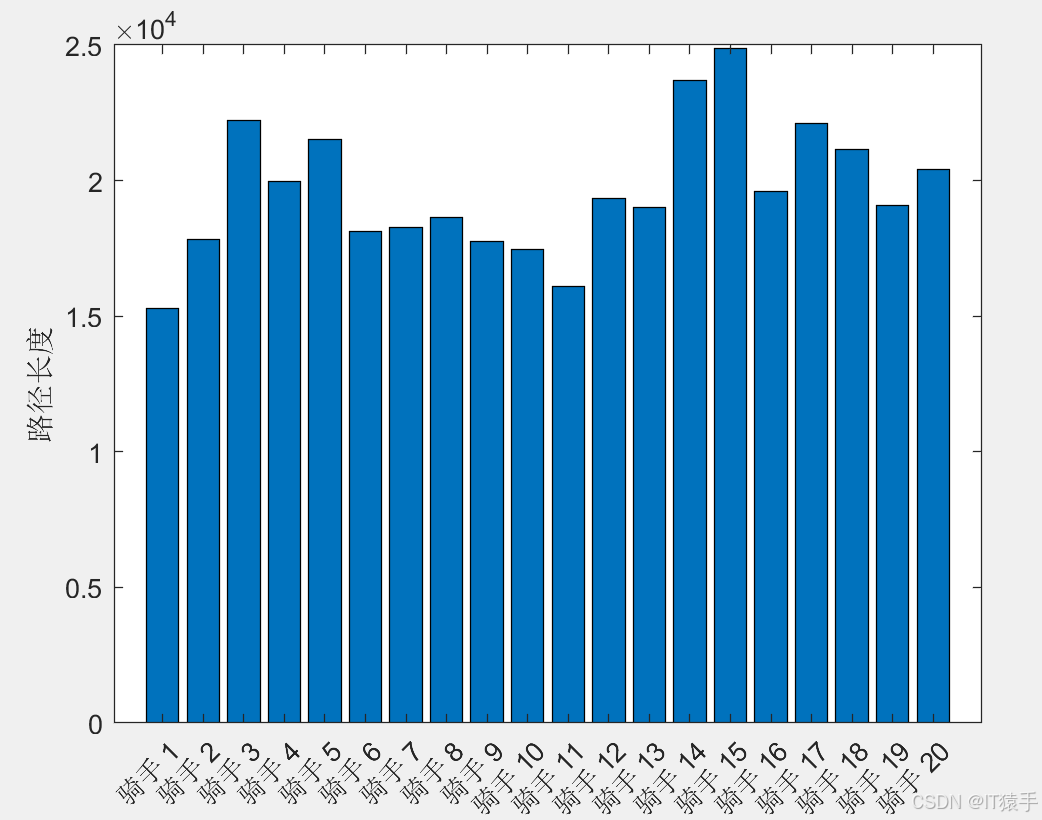
bar(path_length)
ylabel('路径长度')
set(gca,'xtick',1:1:m);
set(gca,'XTickLabel',salemans)

八、完整MATLAB见下方名片