今天开始看到损失函数(错误函数)求解时,可以用最小二乘法,Andrew Ng视频中讲的梯度下降法,于是决定学习梯度下降法求损失函数的最小值,如下:
比如估计函数如下,例子源自这里:
损失函数表示为:
最后主要是求 的最小值,上面公式中利用估计值与真实值y(i)差的平方作为错误估计函数,1/2是为了在求导的时候,消去平方项的系数。
梯度下降法又称最速下降法
原理是:将函数比作一座山,站在某个山坡上,往四周看,从哪个方向向下走一小步,能够下降的最快;
首先,对J(theta)求偏导得到
θi会向着梯度最小的方向进行减少。θi表示更新之前的值,-后面的部分表示按梯度方向减少的量,α表示步长,也就是每次按照梯度减少的方向变化多少。
具体如下:
其中a决定了下降的步伐,负号后面的导数部分决定了下降的方向
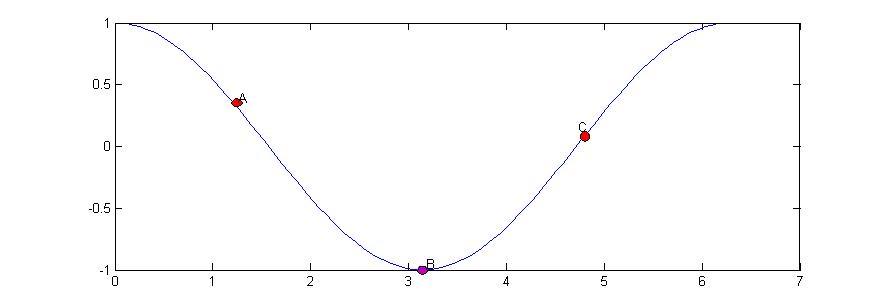
在一维空间内可以理解为
如上图所示如果当前点为A,那么A点的偏导数小于0,也就是斜率小于0.那么此时A应该往右走找到B才是正确的方向,也就是说
此时应该是A的横坐标+A的偏导数的相反数*系数
同理:对于C点,此时应该是向左走才是正确的方向,C点的偏导数大于0,
应该表示为
C点的横坐标+C点偏导数的相反数。这个形象的描述了上面的公式。
通过循环迭代的方法,使得 当连续两点之间的函数值小于一个给定的阈值时,循环结束,停止下降,得到极小值。
步长太小 就会出现局部极小的现象 就像一个小坑里跳不出来,步长大一些就可以跳过局部极值 但是会在 极值左右不断震荡。
C++代码为:(本段摘自这里)
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double e=0.00001;//定义迭代精度
double alpha=0.5;//定义迭代步长
double x=0;//初始化x
double y0=x*x-3*x+2;//与初始化x对应的y值
double y1=0;//定义变量,用于保存当前值
while (true)
{
x=x-alpha*(2.0*x-3.0);
y1=x*x-3*x+2;
if (abs(y1-y0)<e)//如果2次迭代的结果变化很小,结束迭代
{
break;
}
y0=y1;//更新迭代的结果
}
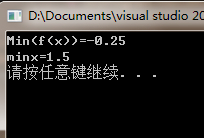
cout<<"Min(f(x))="<<y0<<endl;
cout<<"minx="<<x<<endl;
return 0;
}
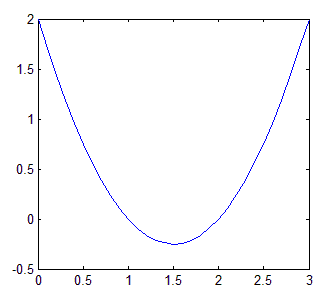
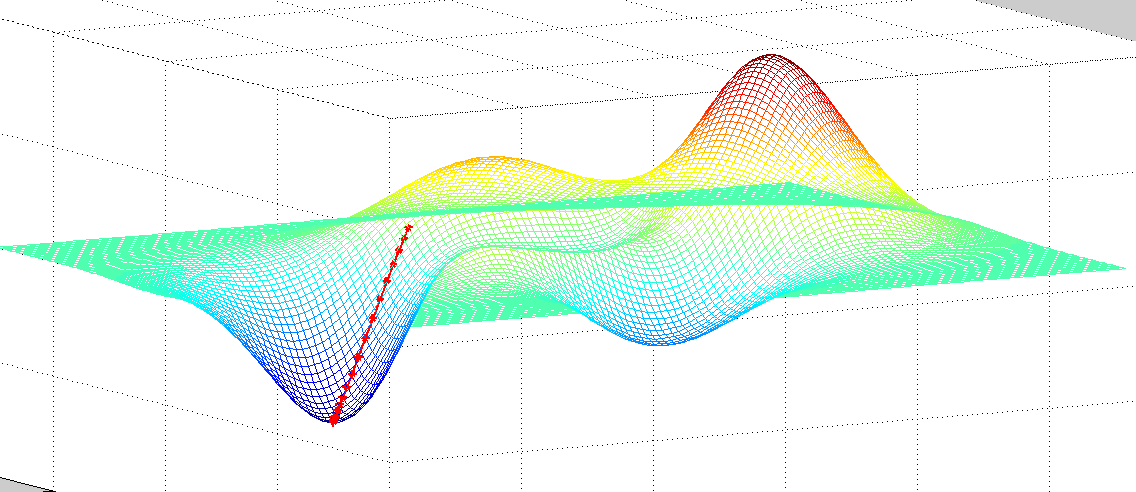
三维图中显示如下:








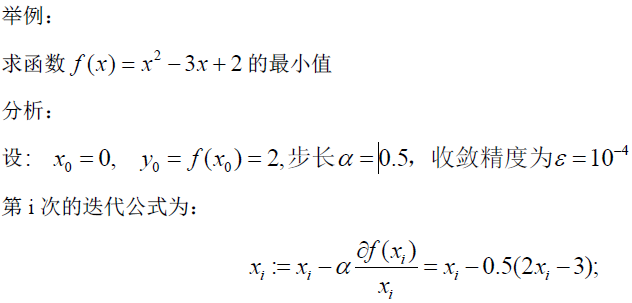














 1333
1333

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








