完全平方数和质因子

质因子

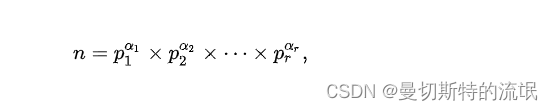
其中p1,p2…pr为质因子

完全平方数

首先一个数字一定可以质因数分解开,如果质因数乘积分解开后,他的幂指数均为偶数,那么这个数字一定是完全平方数

例题

完全平方数

给出一个数a找出一个数b 要求a*b=一个完全平方数,并且b最小

分析:既然要求b最小,那么我只需要将a进行质因数分解,找出那些质因子的幂为奇数个,将这些质因子相乘在一起即为b的结果

eg: 12=2^2 * 3 那么将12*b转为最小完全平方数为36
转为 2^2 * 3 * 3 =36需要一个3

#include<bits/stdc++.h>
#define ll long long

using namespace std;

const int N=1e4+10;
ll n,m,k;



int main() {

	cin>>n;
	
	ll res=1;
	
	for(ll i=2;i*i<=n;i++){//从2开始分解 2将n化为一个奇数,n越化越小 
		if(n%i==0){//质因数 
			int s=0;//记录质因数的幂的次数 
			while(n%i==0)s++,n/=i;//一直分解
			if(s&1)res*=i;//s为奇数 
		} 
	}
	if(n>1)res*=n;//n有剩余
	cout<<res<<endl; 
	
	 

	return 0;
}