本人学艺不精,如有错误,敬请指出……
如有证明上的问题,可以在评论区提出,我看到后会回答
先进一下这个网站(然后就有图了……)
基本知识
如图在 R t △ A B C Rt\triangle ABC Rt△ABC中, ∠ C = 9 0 ∘ \angle C = 90^\circ ∠C=90∘

锐角三角函数就是关于三角形三边的关系。
而锐角三角函数引申出来就变为了三角函数。
我们的角度可以为任意角,甚至大于 36 0 ∘ 360^\circ 360∘或者为负数。
此时如下图:
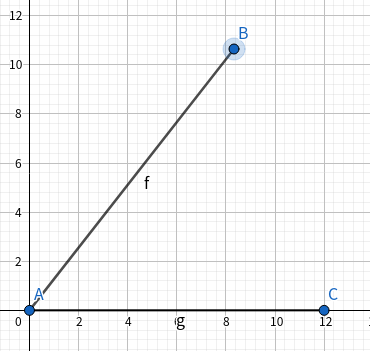
我们这时 a = y a=y a=y, b = x b=x b=x, c = r c=r c=r(其中 x x x, y y y是 B B B点坐标, r r r是线段 A B AB AB的长度)
基本的三角函数 :
sin α = a c \sin \alpha = \dfrac{a}{c} sinα=ca
图象:
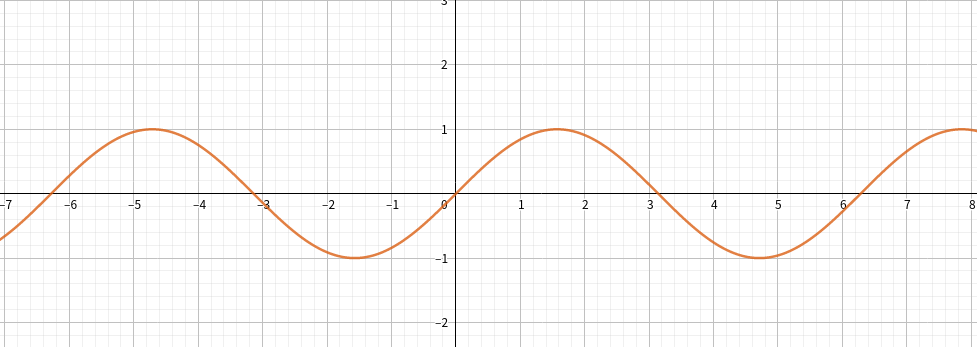
cos α = b c \cos \alpha = \dfrac{b}{c} cosα=cb
图象:
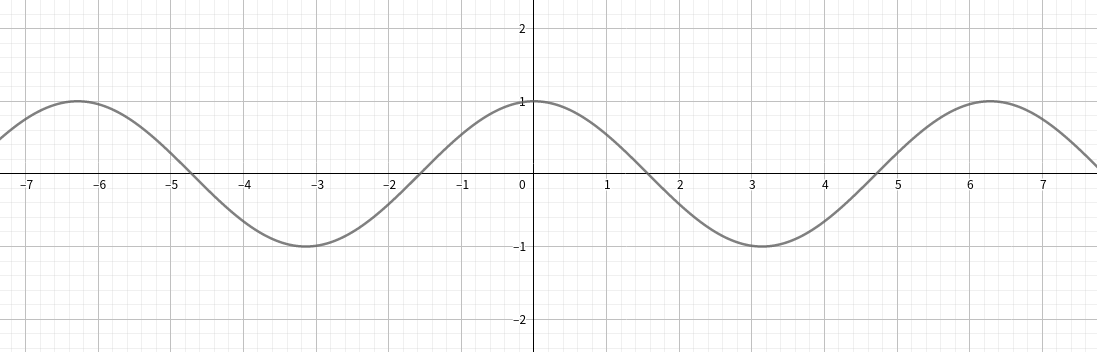
tan
α
=
a
b
\tan \alpha = \dfrac{a}{b}
tanα=ba
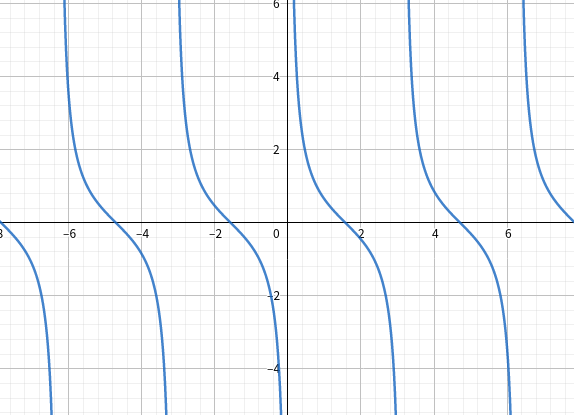
图象:
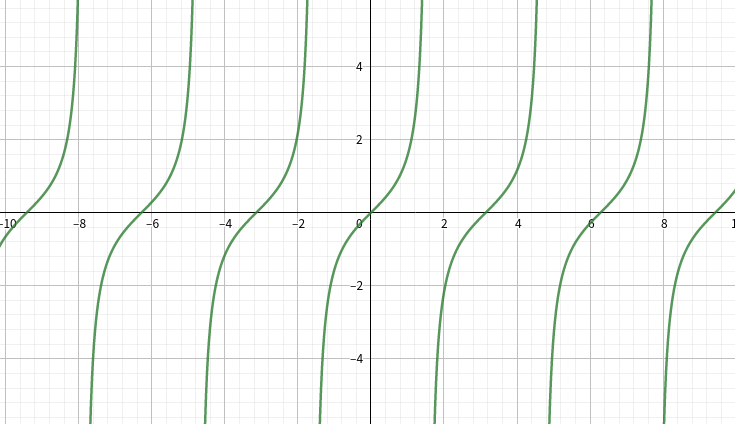
cot
α
=
b
a
\cot \alpha = \dfrac{b}{a}
cotα=ab
图象:
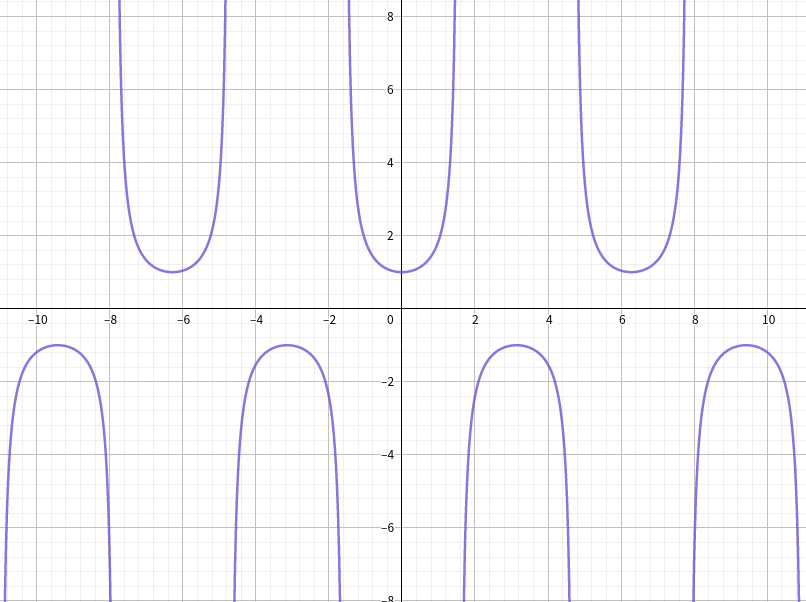
sec
α
=
c
b
\sec \alpha = \dfrac{c}{b}
secα=bc
图象:
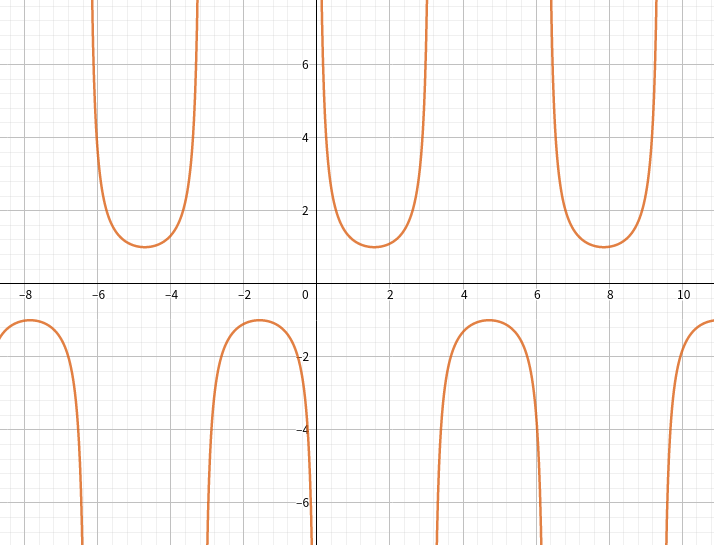
csc
α
=
c
a
\csc \alpha = \dfrac{c}{a}
cscα=ac
图象:
这中间的函数中有很多相似之处,要理解透彻。
三角函数中的关系
sin α = cos ( 9 0 ∘ − α ) \sin \alpha = \cos (90^\circ-\alpha) sinα=cos(90∘−α)
cos α = sin ( 9 0 ∘ − α ) \cos \alpha = \sin (90^\circ-\alpha) cosα=sin(90∘−α)
sin 2 α + cos 2 α = 1 \sin^2 \alpha + \cos^2 \alpha = 1 sin2α+cos2α=1
tan α ⋅ cot α = 1 \tan \alpha \cdot \cot \alpha = 1 tanα⋅cotα=1
tan α = sin α cos α \tan \alpha = \dfrac{\sin \alpha}{\cos \alpha} tanα=cosαsinα
cot α = cos α sin α \cot \alpha = \dfrac{\cos \alpha}{\sin \alpha} cotα=sinαcosα
注意:前两条一定得在锐角三角函数中才能成立。
三角函数常用公式
注意:下面公式在任意值的三角函数中都满足条件。
两角和与差
cos ( α + β ) = cos α ⋅ cos β − sin α ⋅ sin β \cos (\alpha + \beta) = \cos \alpha \cdot \cos\beta - \sin \alpha \cdot \sin\beta cos(α+β)=cosα⋅cosβ−sinα⋅sinβ
cos ( α − β ) = cos α ⋅ cos β + sin α ⋅ sin β \cos(\alpha-\beta)=\cos \alpha \cdot \cos\beta + \sin \alpha \cdot \sin\beta cos(α−β)=cosα⋅cosβ+sinα⋅sinβ
sin ( α + β ) = sin α ⋅ cos β + cos α ⋅ sin β \sin(\alpha+\beta)=\sin\alpha\cdot\cos\beta+\cos\alpha\cdot\sin\beta sin(α+β)=sinα⋅cosβ+cosα⋅sinβ
sin ( α − β ) = sin α ⋅ cos β − cos α ⋅ sin β \sin(\alpha-\beta)=\sin\alpha\cdot\cos\beta-\cos\alpha\cdot\sin\beta sin(α−β)=sinα⋅cosβ−cosα⋅sinβ
三角和与差
sin ( α + β + γ ) = sin α ⋅ cos β ⋅ cos γ + cos α ⋅ sin β ⋅ cos γ + cos α ⋅ cos β ⋅ sin γ − sin α ⋅ sin β ⋅ sin γ \sin(\alpha+\beta+\gamma)=\sin\alpha\cdot\cos\beta\cdot\cos\gamma+\cos\alpha\cdot\sin\beta\cdot\cos\gamma+\cos\alpha\cdot\cos\beta\cdot\sin\gamma-\sin\alpha\cdot\sin\beta\cdot\sin\gamma sin(α+β+γ)=sinα⋅cosβ⋅cosγ+cosα⋅sinβ⋅cosγ+cosα⋅cosβ⋅sinγ−sinα⋅sinβ⋅sinγ
c o s ( α + β + γ ) = c o s α ⋅ cos β ⋅ cos γ − cos α ⋅ sin β ⋅ sin γ − sin α ⋅ cos β ⋅ sin γ − sin α ⋅ sin β ⋅ cos γ cos(\alpha+\beta+\gamma)=cos\alpha\cdot\cos\beta\cdot\cos\gamma-\cos\alpha\cdot\sin\beta\cdot\sin\gamma-\sin\alpha\cdot\cos\beta\cdot\sin\gamma-\sin\alpha\cdot\sin\beta\cdot\cos\gamma cos(α+β+γ)=cosα⋅cosβ⋅cosγ−cosα⋅sinβ⋅sinγ−sinα⋅cosβ⋅sinγ−sinα⋅sinβ⋅cosγ
tan ( α + β + γ ) = tan α + tan β + tan γ − tan α ⋅ tan β ⋅ tan γ 1 − tan α ⋅ tan β − tan α ⋅ tan γ − tan β ⋅ tan γ \tan(\alpha+\beta+\gamma)=\dfrac{\tan\alpha+\tan\beta+\tan\gamma-\tan\alpha\cdot\tan\beta\cdot\tan\gamma}{1-\tan\alpha\cdot\tan\beta-\tan\alpha\cdot\tan\gamma-\tan\beta\cdot\tan\gamma} tan(α+β+γ)=1−tanα⋅tanβ−tanα⋅tanγ−tanβ⋅tanγtanα+tanβ+tanγ−tanα⋅tanβ⋅tanγ
和差化积
sin α + sin β = 2 ⋅ sin ( α + β 2 ) ⋅ cos ( α − β 2 ) \sin\alpha+\sin\beta=2\cdot\sin(\dfrac{\alpha+\beta}{2})\cdot\cos(\dfrac{\alpha-\beta}{2}) sinα+sinβ=2⋅sin(2α+β)⋅cos(2α−β)
sin α − sin β = 2 ⋅ sin ( α − β 2 ) ⋅ cos ( α + β 2 ) \sin\alpha-\sin\beta=2\cdot\sin(\dfrac{\alpha-\beta}{2})\cdot\cos(\dfrac{\alpha+\beta}{2}) sinα−sinβ=2⋅sin(2α−β)⋅cos(2α+β)
cos α + cos β = 2 ⋅ cos ( α + β 2 ) ⋅ cos ( α − β 2 ) \cos\alpha+\cos\beta=2\cdot\cos(\dfrac{\alpha+\beta}{2})\cdot\cos(\dfrac{\alpha-\beta}{2}) cosα+cosβ=2⋅cos(2α+β)⋅cos(2α−β)
cos α − cos β = − 2 ⋅ sin ( α + β 2 ) ⋅ sin ( α − β 2 ) \cos\alpha-\cos\beta=-2\cdot\sin(\dfrac{\alpha+\beta}{2})\cdot\sin(\dfrac{\alpha-\beta}{2}) cosα−cosβ=−2⋅sin(2α+β)⋅sin(2α−β)
二倍角公式
这其实就是两角和。
sin
2
α
=
2
⋅
sin
α
⋅
cos
α
=
2
tan
α
+
cot
α
\sin 2\alpha = 2\cdot\sin\alpha\cdot\cos\alpha=\dfrac{2}{\tan\alpha+\cot\alpha}
sin2α=2⋅sinα⋅cosα=tanα+cotα2
cos 2 α = cos 2 α − sin 2 α = 2 α − 1 = 1 − 2 ⋅ sin 2 α \cos 2\alpha = \cos^2\alpha-\sin^2\alpha=2\alpha-1=1-2\cdot\sin^2\alpha cos2α=cos2α−sin2α=2α−1=1−2⋅sin2α
tan 2 α = 2 ⋅ tan α 1 − tan 2 α \tan 2\alpha=\dfrac{2\cdot\tan\alpha}{1-\tan^2\alpha} tan2α=1−tan2α2⋅tanα
cot 2 α = cot 2 α − 1 2 ⋅ cot α \cot 2\alpha=\dfrac{\cot^2\alpha-1}{2\cdot\cot\alpha} cot2α=2⋅cotαcot2α−1
sec 2 α = sec 2 α 1 − tan 2 α \sec 2\alpha=\dfrac{\sec^2\alpha}{1-\tan^2\alpha} sec2α=1−tan2αsec2α
半角公式
注意:正负由
α
2
\dfrac{\alpha}{2}
2α所在象限决定。
sin
(
α
2
)
=
±
1
−
cos
α
2
\sin(\dfrac{\alpha}{2})=\pm\sqrt{\dfrac{1-\cos\alpha}{2}}
sin(2α)=±21−cosα
cos ( a 2 ) = ± 1 + cos α 2 \cos(\dfrac{a}{2})=\pm\sqrt{\dfrac{1+\cos\alpha}{2}} cos(2a)=±21+cosα
tan ( α 2 ) = ± 1 − c o s α 1 + c o s α = sin α 1 + cos α = 1 − cos α sin α = csc α − cot α \tan(\dfrac{\alpha}{2})=\pm\sqrt{\dfrac{1-cos\alpha}{1+cos\alpha}}=\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{1-\cos\alpha}{\sin\alpha}=\csc\alpha-\cot\alpha tan(2α)=±1+cosα1−cosα=1+cosαsinα=sinα1−cosα=cscα−cotα
cot ( α 2 ) = ± 1 + cos α 1 − cos α = 1 + cos α sin α = sin α 1 − cos α = csc α + cot α \cot(\dfrac{\alpha}{2})=\pm\sqrt{\dfrac{1+\cos\alpha}{1-\cos\alpha}}=\dfrac{1+\cos\alpha}{\sin\alpha}=\dfrac{\sin\alpha}{1-\cos\alpha}=\csc\alpha+\cot\alpha cot(2α)=±1−cosα1+cosα=sinα1+cosα=1−cosαsinα=cscα+cotα
sec ( α 2 ) = ± 2 ⋅ sec α sec α + 1 \sec(\dfrac{\alpha}{2})=\pm\sqrt{\dfrac{2\cdot\sec\alpha}{\sec\alpha+1}} sec(2α)=±secα+12⋅secα
csc ( α 2 ) = ± 2 ⋅ sec α sec α − 1 \csc(\dfrac{\alpha}{2})=\pm\sqrt{\dfrac{2\cdot\sec\alpha}{\sec\alpha-1}} csc(2α)=±secα−12⋅secα
降幂公式
sin 2 α = 1 − cos ( 2 α ) 2 \sin^2\alpha=\dfrac{1-\cos(2\alpha)}{2} sin2α=21−cos(2α)
cos 2 α = 1 + cos ( 2 α ) 2 \cos^2\alpha=\dfrac{1+\cos(2\alpha)}{2} cos2α=21+cos(2α)
tan 2 α = 1 − c o s ( 2 α ) 1 + c o s ( 2 α ) \tan^2\alpha=\dfrac{1-cos(2\alpha)}{1+cos(2\alpha)} tan2α=1+cos(2α)1−cos(2α)
诱导公式
太多了,我都不想打了,有时间再补,溜了溜了
三角函数常用定理
正弦定理
设在 △ A B C \triangle ABC △ABC中, ∠ A \angle A ∠A、 ∠ B \angle B ∠B、 ∠ C \angle C ∠C的对边边长分别是 a a a、 b b b、 c c c, △ A B C \triangle_{ABC} △ABC的外接圆的半径长为 r r r,则有:
sin A a = sin B b = sin C c \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} asinA=bsinB=csinC
也可表示为
a sin A = b sin B = c sin C = 2 r \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2r sinAa=sinBb=sinCc=2r
正弦定理可以用与求三角形面积:
S △ A B C = a ⋅ b ⋅ sin C 2 = b ⋅ c ⋅ sin A 2 = a ⋅ c ⋅ sin A 2 S_{\triangle ABC}=\dfrac{a \cdot b \cdot \sin C}{2}=\dfrac{b \cdot c \cdot \sin A}{2}=\dfrac{a \cdot c \cdot \sin A}{2} S△ABC=2a⋅b⋅sinC=2b⋅c⋅sinA=2a⋅c⋅sinA
余弦定理
设在 △ A B C \triangle ABC △ABC中, ∠ A \angle A ∠A、 ∠ B \angle B ∠B、 ∠ C \angle C ∠C的对边边长分别是 a a a、 b b b、 c c c, △ A B C \triangle_{ABC} △ABC,则有:
a 2 = b 2 + c 2 − 2 ⋅ b ⋅ c ⋅ cos A a^2=b^2+c^2-2\cdot b\cdot c\cdot \cos A a2=b2+c2−2⋅b⋅c⋅cosA
b 2 = a 2 + c 2 − 2 ⋅ a ⋅ b ⋅ cos B b^2 = a^2 + c^2 - 2 \cdot a \cdot b \cdot \cos B b2=a2+c2−2⋅a⋅b⋅cosB
c 2 = a 2 + b 2 − 2 ⋅ a ⋅ b ⋅ cos C c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos C c2=a2+b2−2⋅a⋅b⋅cosC
也可表示为:
cos A = ( b 2 + c 2 − a 2 ) 2 ⋅ b ⋅ c \cos A = \dfrac {(b^2 + c^2 - a^2)}{2\cdot b\cdot c} cosA=2⋅b⋅c(b2+c2−a2)
cos B = ( a 2 + c 2 − b 2 ) 2 ⋅ a ⋅ c \cos B = \dfrac {(a^2 + c^2 - b^2)}{2\cdot a\cdot c} cosB=2⋅a⋅c(a2+c2−b2)
cos C = ( a 2 + b 2 − c 2 ) 2 ⋅ a ⋅ b \cos C = \dfrac {(a^2 + b^2 - c^2)}{2\cdot a\cdot b} cosC=2⋅a⋅b(a2+b2−c2)
正切定理
设在 △ A B C \triangle ABC △ABC中, ∠ A \angle A ∠A、 ∠ B \angle B ∠B、 ∠ C \angle C ∠C的对边边长分别是 a a a、 b b b、 c c c, △ A B C \triangle_{ABC} △ABC,则有:
a + b a − b = tan A + B 2 tan A − B 2 \dfrac{a+b}{a-b}=\dfrac{\tan\dfrac{A+B}{2}}{\tan\dfrac{A-B}{2}} a−ba+b=tan2A−Btan2A+B























 2550
2550











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








