DX11龙书学习笔记---变换

1、仿射变换

- 齐次坐标

在齐次坐标中，我们使用4个元素，我们通过它的第4个坐标分量w来决定所描述的是一个点还是一个向量。确切地说，我们写为：
1．(x,y,z,0)用于向量
2．(x,y,z,1)用于点

- 定义和矩阵表示

一个线性变换无法表示所有我们需要的变换；所以，我们需要添加一组叫做仿射变换的函数。仿射变换是一个线性变换加上一个平移向量b；也就是：

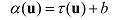
或者用矩阵表示为：

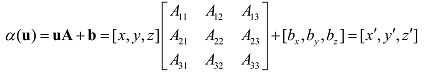
式中的A是线性变换的矩阵表示。
如果使用w=1的齐次坐标，则可表示为：

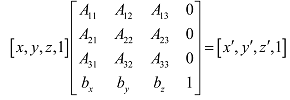
公式中的4×4矩阵称为仿射矩阵的矩阵表示。

- 平移

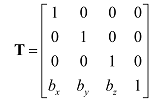
这个矩阵称之为平移矩阵。
平移矩阵的逆矩阵如下：

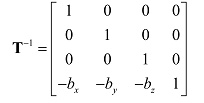
- 缩放和旋转的仿射矩阵

若b=0，仿射变换就退化为一个线性变换。我们可以将任何一个线性变换表示成b=0的仿射变换。换句话说，我们可以用一个4×4仿射矩阵表示任意一个线性变换。例如，缩放和旋转矩阵可以用4×4矩阵写成如下形式：

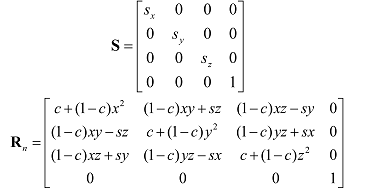
2、坐标转换变换

-定义

我们将一个点或向量的坐标从一个参考系转换到另一个不同的参考系。我们将这种把坐标从一个参考系转换到另一个参考系的变换称为坐标转换变换（change of coordinate transformation）。
由于位置是点的属性，而不是向量的属性，所以点和向量在实现坐标转换变换时要区别对待，使用不同的处理方式。

-向量的坐标变换

由于向量没有位置信息，故对向量的坐标变换可以把变换前后的坐标系平移至原点重合进行。考虑向量p=（x，y）在二维坐标系A中，它可以用线性组合方式表示为：

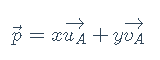
其中，u、v是p坐标系A的基，上式写成线性组合的形式即：

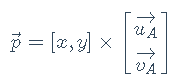
u、v通常是单位正交基。此时如果想改变研究的坐标系为B，那么在坐标系B下的p为：

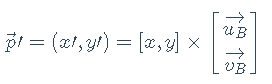
此时的u、v坐标为在坐标系B中的坐标。也就是说，如果已知原坐标系的各轴向基向量在待变换坐标系的向量表示，把这些基向量按行依次排列得到的矩阵即向量的坐标系变换矩阵。显然这一结论对高维坐标系转换也成立。3维向量的坐标系变换公式为：

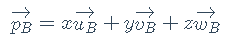
- 点的坐标变换

点的坐标变换则有所不同，对点的平移会改变点的位置。那么，在对点进行坐标系变换的时候就需要加上相对偏移，这个偏移用向量V表示。假设变换前坐标系为A，待变换坐标系为B，点的坐标为p，在不考虑偏移时，点的坐标变换和向量一样：

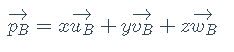
显然，V为坐标系B的原点指向坐标系A的原点的向量，即：

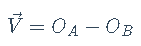
由于是在变换后再加上偏移值，故上式应是坐标系B中的表示。那么，完整的点的坐标变换公式为：

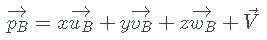
- 矩阵表示

参照之前齐次坐标的内容，同样可以很容易地对这两种情况作统一处理。扩展第四维w，w为0表示向量，w为1表示点，同时把变换矩阵M扩展为四维齐次矩阵C：

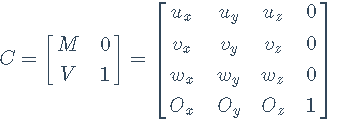
这个矩阵也很好理解，其中的每一行都是一个齐次坐标。前三行分别是原坐标系的基向量在待变换坐标系的齐次坐标，故其w值为0；第四行为偏移量，值相当于原坐标系原点在待变换坐标系的坐标，故其w值为1。