文章目录
第五课——支持向量机SVM
一、约束优化知识复习
约束优化问题与KKT条件
约束优化问题由如下三部分组成
目标函数
变量
约束条件
目标:找到满足约束条件的变量,使得目标函数的值达到最大或最小。
对于一般的约束优化问题
min
f
(
x
)
s
.
t
.
g
j
(
x
)
=
0
,
j
=
1
,
2
,
.
.
.
,
n
h
i
(
x
)
≤
0
,
i
=
1
,
2
,
.
.
.
,
m
\text{min}f(x)\\ s.t.\ g_j(x)=0,\ j=1,2,...,n\\ \quad\ h_i(x)\le 0,\ i=1,2,...,m\\
minf(x)s.t. gj(x)=0, j=1,2,...,n hi(x)≤0, i=1,2,...,m
通过引入新的变量𝜆𝑖和a𝑗,将所有的等式、不等式约束以及𝑓(𝑥)构造拉格朗日函数:
L
(
x
,
λ
,
a
)
=
f
(
x
)
+
∑
j
a
j
g
j
(
x
)
+
∑
i
λ
i
h
i
(
x
)
L(x,\lambda,a)=f(x)+\sum_ja_jg_j(x)+\sum_i\lambda_ih_i(x)
L(x,λ,a)=f(x)+j∑ajgj(x)+i∑λihi(x)
其最优解
x
∗
x^*
x∗满足KKT条件(Kuhn-Tucker conditions)
KKT(Karush-Kuhn-Tucker)条件,是非线性规划领域里最重要的理论成果之一,是确定某点为极值点的必要条件。对于凸规划,KKT点就是优化极值点(充分必要条件)。
如果一个点x是满足所有约束的极值点,那么该点x就要满足一下所有条件,即KKT条件

对朗格朗日乘子λ分两种情况
λ
i
≥
0
,
λ
i
h
i
(
x
∗
)
=
0
⇒
{
λ
=
0
,
h
(
x
∗
)
<
0
λ
>
0
,
h
(
x
∗
)
=
0
①
h
(
x
)
不
起
作
用
⇒
h
(
x
∗
)
<
0
⇒
无
约
束
优
化
⇒
λ
=
0
②
h
(
x
)
起
作
用
⇒
h
(
x
∗
)
=
0
,
λ
>
0
\begin{aligned} &\lambda_i\ge0,\lambda_ih_i(x^*)=0\Rightarrow\begin{cases} \lambda =0,h(x^*)<0\\ \lambda>0,h(x^*)=0 \end{cases}\\ &①\ h(x)不起作用\Rightarrow h(x^*)<0\Rightarrow 无约束优化\Rightarrow \lambda=0\\ &②\ h(x)起作用\Rightarrow h(x^*)=0,\lambda>0 \end{aligned}
λi≥0,λihi(x∗)=0⇒{λ=0,h(x∗)<0λ>0,h(x∗)=0① h(x)不起作用⇒h(x∗)<0⇒无约束优化⇒λ=0② h(x)起作用⇒h(x∗)=0,λ>0
对于下图:

L
(
u
,
λ
)
=
u
2
−
λ
(
u
−
b
)
∇
u
L
(
u
,
λ
)
=
2
u
−
λ
=
0
⇒
u
=
λ
2
最
优
解
u
∗
,
u
∗
=
λ
2
K
K
T
:
u
∗
−
b
≥
0
λ
(
u
∗
−
b
)
=
0
对
于
情
况
1
:
b
>
0
⇒
(
λ
2
−
b
)
=
0
起
到
了
约
束
作
用
⇒
λ
=
2
b
对
于
情
况
2
:
b
<
0
⇒
(
λ
2
−
b
)
=
0
没
有
起
到
约
束
作
用
⇒
λ
=
0
\begin{aligned} &L(u,\lambda)=u^2-\lambda(u-b)\\ &\nabla_uL(u,\lambda)=2u-\lambda=0\Rightarrow u=\frac{\lambda}{2}\\ &最优解u^*,u^*=\frac{\lambda}{2}\\ &KKT:u^*-b\ge 0\quad \lambda(u^*-b)=0\\ &对于情况1: b>0\Rightarrow (\frac{\lambda}{2}-b)=0\ 起到了约束作用\Rightarrow \lambda=2b\\ &对于情况2: b<0\Rightarrow (\frac{\lambda}{2}-b)=0\ 没有起到约束作用\Rightarrow\lambda=0 \end{aligned}
L(u,λ)=u2−λ(u−b)∇uL(u,λ)=2u−λ=0⇒u=2λ最优解u∗,u∗=2λKKT:u∗−b≥0λ(u∗−b)=0对于情况1:b>0⇒(2λ−b)=0 起到了约束作用⇒λ=2b对于情况2:b<0⇒(2λ−b)=0 没有起到约束作用⇒λ=0
对偶问题
通过拉格朗日乘子可以将约束优化问题转化为对偶问题(将参数转为拉格朗日乘子)。
主问题最小化->对偶问题最大化;或者主问题最大化->对偶问题最小化
当优化问题的对偶形式更容易求解时,使用对偶方程进行求解
对于主问题
min
w
f
0
(
w
)
s.t.
f
i
(
w
)
≤
0
,
i
=
1
,
.
.
.
,
k
\begin{aligned} &\underset{w}{\text{min}}f_0(w)\\ &\text{s.t.}\ f_i(w)\le 0,i=1,...,k \end{aligned}
wminf0(w)s.t. fi(w)≤0,i=1,...,k
利用拉格朗日乘子得到无约束优化问题
L
(
w
,
α
)
=
f
0
(
w
)
+
∑
i
=
1
k
α
i
f
i
(
w
)
L(w,\alpha)=f_0(w)+\sum_{i=1}^k \alpha_if_i(w)
L(w,α)=f0(w)+i=1∑kαifi(w)
定理
i
f
w
满
足
主
问
题
约
束
,
max
α
i
≥
0
L
(
w
,
α
)
=
f
0
(
w
)
if\ w满足主问题约束,\ \underset{\alpha_i\ge 0}{\text{max}}L(w,\alpha)=f_0(w)
if w满足主问题约束, αi≥0maxL(w,α)=f0(w)
即,当有拉格朗日乘子约束时, L ( w , α ) 的 最 大 值 为 f 0 ( x ) L(w,α)的最大值为f_0(x) L(w,α)的最大值为f0(x)
主问题重写为 min w max a i ≥ 0 L ( w , α ) \text{min}_w\text{max}_{a_i\ge0}\ L(w,\alpha) minwmaxai≥0 L(w,α)
上述主问题的对偶问题为 max a i ≥ 0 min w L ( w , α ) \text{max}_{a_i\ge0}\text{min}_w\ L(w,\alpha) maxai≥0minw L(w,α)
弱对偶性
d
=
max
a
i
≥
0
min
w
L
(
w
,
α
)
≤
min
w
max
a
i
≥
0
L
(
w
,
α
)
=
p
d=\text{max}_{a_i\ge0}\text{min}_w\ L(w,\alpha)\le\text{min}_w\text{max}_{a_i\ge0}\ L(w,\alpha)=p
d=maxai≥0minw L(w,α)≤minwmaxai≥0 L(w,α)=p
强对偶性:𝑑=p(当主问题为凸优化问题)
实例说明

L
(
u
,
λ
)
=
u
2
−
λ
(
u
−
b
)
∇
u
L
(
u
,
λ
)
=
2
u
−
λ
=
0
⇒
u
=
λ
2
对
偶
问
题
max
α
min
(
u
2
−
α
(
u
−
b
)
)
=
max
α
(
−
α
2
2
+
b
α
)
s
.
t
.
α
≥
0
\begin{aligned} &L(u,\lambda)=u^2-\lambda(u-b)\\ &\nabla_uL(u,\lambda)=2u-\lambda=0\Rightarrow u=\frac{\lambda}{2}\\ &对偶问题\underset{\alpha}{\text{max}}\ \text{min}(u^2-\alpha(u-b))=\underset{\alpha}{\text{max}}(-\frac{\alpha^2}{2}+b\alpha)\quad s.t. \alpha\ge 0\\ \end{aligned}
L(u,λ)=u2−λ(u−b)∇uL(u,λ)=2u−λ=0⇒u=2λ对偶问题αmax min(u2−α(u−b))=αmax(−2α2+bα)s.t.α≥0
二、SVM问题
SVM简介
支持向量机(Support Vector Machines)最早在上世纪90 年代由Vapnik 等人提出
在深度学习时代(2012)之前,SVM被认为机器学习中近十几年来最成功,表现最好的算法。
在手写字符识别上,测试误差仅为 1.1% (1994)
LeNet(784-192-30-10), 测试误差为 0.9% (1998)
最近的卷积神经网络模型,测试误差大约为 0.6%
问题的引入
❓ 针对二分类问题,给定线性可分的训练样本,可以找到很多的超平面将训练样本分开,那么哪一个划分超平面是最优的?
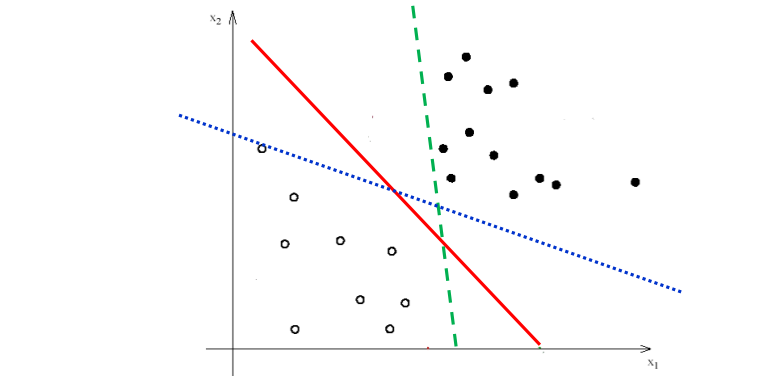
我们可以定义线性分类器的“间隔margin”:到击中边界可以增加的宽度
宽度越大说明分类面越好,可以容忍更多的噪声

线性可分SVM
线性可分SVM选择具有“最大间隔”的分类超平面。
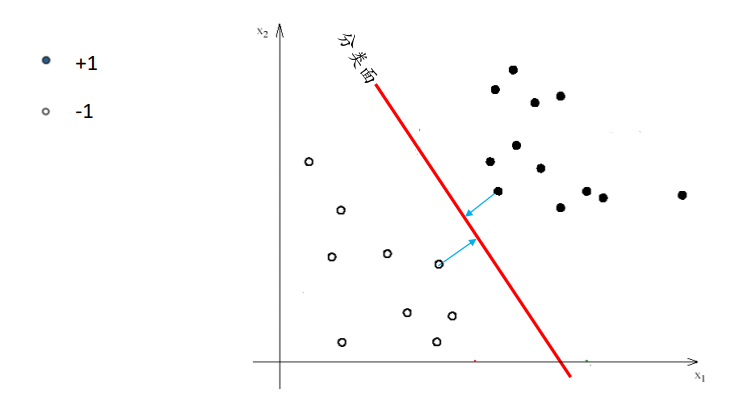
线性可分SVM的核心:学习一个具有最大间隔的划分超平面
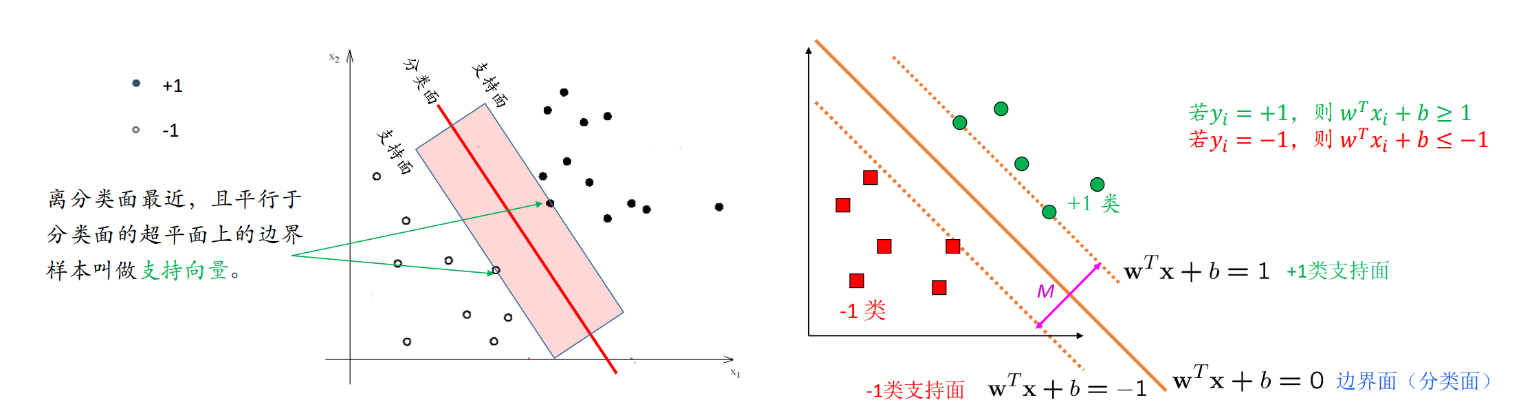
使用超平面方程 w T x + b = 0 w^Tx+b=0 wTx+b=0表示分类面, w T x + b = ± 1 w^Tx+b=\pm 1 wTx+b=±1表示支持面
分类面由穿过支持面的样本点决定
一开始并不知道那些样本点是支持向量
样本的标签被设置为了-1和+1
训练时使用训练集训练出w和b,然后测试时根据 w T + b w^T+b wT+b的值大于0还是小于0来判断是属于+1类还是-1类
SVM要求两类支持面的距离 M 尽可能大
间隔M建模
向量w与支持面、分类面正交:x1和x2是+1类的样本点

使用w和b对M建模
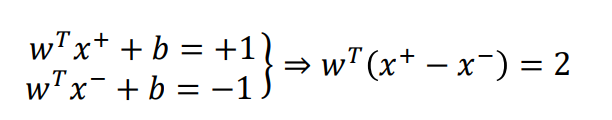
因为 a T b = ∣ ∣ a ∣ ∣ ∥ ∣ b ∣ ∣ cos θ a^Tb=||a||\||b||\text{cos}\theta aTb=∣∣a∣∣∥∣b∣∣cosθ,这里的θ=0
则有

问题简化为求两个支持面与w的两个交点x+与x-之间的距离

M表达式如下
m
a
r
g
i
n
M
=
∣
∣
x
+
−
x
−
∣
∣
=
2
∣
∣
w
∣
∣
margin\ M=||x^+-x^-||=\frac{2}{||w||}
margin M=∣∣x+−x−∣∣=∣∣w∣∣2
SVM问题建模
这样,最大间隔问题转化成优化问题
max
2
∣
∣
w
∣
∣
⇔
min
∣
∣
w
∣
∣
2
\text{max}\frac{2}{||w||}\Leftrightarrow \text{min}||w||^2
max∣∣w∣∣2⇔min∣∣w∣∣2
该目标的约束条件为
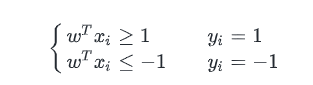
将约束条件(loss function)简化为
y
i
(
w
T
x
i
+
b
)
≥
1
y_i(\pmb w^T\pmb x_i+b)\ge 1
yi(wwwTxxxi+b)≥1
最终,寻找具有最大间隔的划分超平面转化成如下约束问题
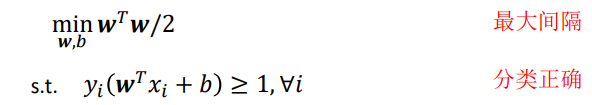
约束里的等号仅在穿过支持面的点(支持向量)处成立
因为最大间隔通过支持面得到,所以不难理解分类超平面仅由支持向量决定
线性可分SVM是一个凸二次规划问题
SVM的对偶问题
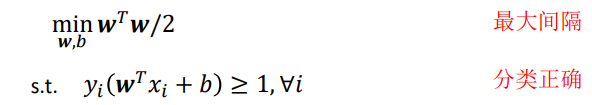
对应的朗格朗日函数如下:
L
(
w
,
b
,
α
)
=
1
2
w
T
w
−
∑
i
=
1
N
α
i
(
y
i
(
w
T
⋅
x
i
+
b
)
−
1
)
∀
i
,
α
i
≥
0
L(w,b,\alpha)=\frac{1}{2}\pmb w^T\pmb w-\sum_{i=1}^N\alpha_i(y_i(\pmb w^T\cdot \pmb x_i+b)-1)\quad \forall i,\alpha_i\ge0
L(w,b,α)=21wwwTwww−i=1∑Nαi(yi(wwwT⋅xxxi+b)−1)∀i,αi≥0
最小化伤处拉格朗日:对w和b求偏导,并且令偏导为0,则有
∇
w
L
(
w
,
b
,
α
)
=
w
−
∑
i
=
1
N
α
i
y
i
x
i
=
0
∇
b
L
(
w
,
b
,
α
)
=
∑
i
=
1
N
α
i
y
i
=
0
\nabla_wL(w,b,\alpha)=w-\sum_{i=1}^{N}\alpha_iy_ix_i=0\\ \nabla_bL(w,b,\alpha)=\sum_{i=1}^{N}\alpha_iy_i=0
∇wL(w,b,α)=w−i=1∑Nαiyixi=0∇bL(w,b,α)=i=1∑Nαiyi=0
将
w
=
∑
i
=
1
N
α
i
y
i
x
i
,
∑
i
=
1
N
α
i
y
i
=
0
w=\sum_{i=1}^{N}\alpha_iy_ix_i,\sum_{i=1}^{N}\alpha_iy_i=0
w=∑i=1Nαiyixi,∑i=1Nαiyi=0带入朗格朗日函数中,得到对偶问题:
max
α
i
≥
0
min
w
,
b
L
(
w
,
b
,
α
)
L
(
w
,
b
,
α
)
=
1
2
w
T
w
−
∑
i
=
1
N
α
i
(
y
i
(
w
T
⋅
x
i
+
b
)
−
1
)
=
1
2
w
T
w
+
∑
i
=
1
N
α
i
−
∑
i
=
1
N
α
i
y
i
w
T
x
i
−
∑
i
=
1
N
α
i
y
i
b
=
1
2
w
T
w
+
∑
i
=
1
N
α
i
−
∑
i
=
1
N
α
i
y
i
w
T
x
i
=
∑
i
=
1
N
α
i
−
1
2
∑
i
,
j
=
1
α
i
α
j
y
i
y
j
(
x
i
T
x
j
)
s
.
t
.
∑
i
=
1
N
α
i
y
i
=
0
\text{max}_{\alpha_i\ge 0}\text{min}_{w,b}L(w,b,\alpha)\\ \begin{aligned}L(w,b,\alpha) &=\frac{1}{2}\pmb w^T\pmb w-\sum_{i=1}^N\alpha_i(y_i(\pmb w^T\cdot \pmb x_i+b)-1)\\ &=\frac{1}{2}\pmb w^T\pmb w+\sum_{i=1}^N\alpha_i-\sum_{i=1}^N\alpha_iy_i\pmb w^T \pmb x_i-\sum_{i=1}^N\alpha_iy_ib\\ &=\frac{1}{2}\pmb w^T\pmb w+\sum_{i=1}^N\alpha_i-\sum_{i=1}^N\alpha_iy_i\pmb w^T \pmb x_i\\ &=\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{i,j=1}\alpha_i\alpha_jy_iy_j(\pmb x_i^T\pmb x_j)\quad s.t. \sum_{i=1}^{N}\alpha_iy_i=0 \end{aligned}
maxαi≥0minw,bL(w,b,α)L(w,b,α)=21wwwTwww−i=1∑Nαi(yi(wwwT⋅xxxi+b)−1)=21wwwTwww+i=1∑Nαi−i=1∑NαiyiwwwTxxxi−i=1∑Nαiyib=21wwwTwww+i=1∑Nαi−i=1∑NαiyiwwwTxxxi=i=1∑Nαi−21i,j=1∑αiαjyiyj(xxxiTxxxj)s.t.i=1∑Nαiyi=0
对偶问题
max
α
i
{
∑
i
=
1
N
α
i
−
1
2
∑
i
,
j
=
1
α
i
α
j
y
i
y
j
(
x
i
T
x
j
)
}
s
.
t
.
∑
i
=
1
N
α
i
y
i
=
0
α
i
≥
0
\max_{\alpha_i}\{\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{i,j=1}\alpha_i\alpha_jy_iy_j(\pmb x_i^T\pmb x_j)\}\\ s.t. \sum_{i=1}^{N}\alpha_iy_i=0 \quad\alpha_i\ge0
αimax{i=1∑Nαi−21i,j=1∑αiαjyiyj(xxxiTxxxj)}s.t.i=1∑Nαiyi=0αi≥0
解出
α
i
\alpha_i
αi后,利用
w
=
∑
i
=
1
N
α
i
y
i
x
i
w=\sum_{i=1}^{N}\alpha_iy_ix_i
w=∑i=1Nαiyixi得到w
最后,通过支持向量得到b
由原问题的KKT条件
α i ≥ 0 1 − y i ( w T x i + b ) ≤ 0 α i ( 1 − y i ( w T x i + b ) ) = 0 \alpha_i\ge 0\\ 1-y_i(w^Tx_i+b)\le 0\\ \alpha_i(1-y_i(w^Tx_i+b))=0 αi≥01−yi(wTxi+b)≤0αi(1−yi(wTxi+b))=0
则当 α i ≥ 0 \alpha_i\ge0 αi≥0时,此时约束条件起作用, 1 − y i ( w T x i + b ) = 0 1-y_i(w^Tx_i+b)=0 1−yi(wTxi+b)=0从而可以解得b
理论上,可通过任意一个支持向量获得b; 但实际中,通常使用所有支持向量的平均值

在求得模型参数 w,b 后,对于一个测试样本
x
t
e
s
t
x_{test}
xtest ,可通过下式分类
y
^
=
sign
(
w
T
x
t
e
s
t
+
b
)
=
sign
(
∑
i
n
α
i
y
i
x
i
T
x
t
e
s
t
+
b
)
\hat y=\text{sign}(w^Tx_{test}+b)=\text{sign}(\sum_i^n\alpha_iy_ix_i^Tx_{test}+b)
y^=sign(wTxtest+b)=sign(i∑nαiyixiTxtest+b)
依据KKT条件,仅支持向量的的拉格朗日系数不为0,所以分类决策可简化为
y
^
=
sign
(
∑
i
∈
S
u
p
p
o
r
t
V
e
c
t
o
r
s
α
i
y
i
x
i
T
x
t
e
s
t
+
b
)
\hat y=\text{sign}(\sum_{i\in SupportVectors}\alpha_iy_ix_i^Tx_{test}+b)
y^=sign(i∈SupportVectors∑αiyixiTxtest+b)
对偶问题的约束条件比主问题的约束条件简单,然而,对偶问题的规模正比于训练样本数。
SMO (Sequential Minimal Optimization) 序列最小优化算法是求解对偶问题的高效算 法
省事起见,可以调用Python中CVXOPT凸优化包求解
SMO算法思想
基本思路:固定 α i \alpha_i αi之外的所有参数,关于 α i \alpha_i αi求极值
基本步骤:在初始化参数之后,不断执行如下两个步骤直至收敛
1️⃣选取一对需要更新的变量𝛼𝑖和𝛼𝑗
2️⃣固定𝛼𝑖和𝛼𝑗以外的参数,求解更新后的𝛼𝑖和𝛼𝑗
α i y i + α j y j = − ∑ k ≠ i , j α k y k = c \alpha_iy_i+\alpha_jy_j=-\sum_{k\not= i,j}\alpha_ky_k=c αiyi+αjyj=−k=i,j∑αkyk=c
利用 α i y i + α j y j = c \alpha_iy_i+\alpha_jy_j=c αiyi+αjyj=c,得到关于𝛼𝑖的单变量二次规划问题,从而解出𝛼𝑖的闭式解。
举例说明——重要

W ( α ) W(\alpha) W(α)是拉格朗日函数
1️⃣ 对 α 1 , α 2 , α 3 , α 4 α_1,\alpha_2,\alpha_3,\alpha_4 α1,α2,α3,α4赋予初值
2️⃣ 每次更新两个变量:以 α 2 , α 3 \alpha_2,\alpha_3 α2,α3为例
α 2 − α 3 = α 4 − α 1 = C ⇒ α 2 = α 3 + C \alpha_2-\alpha_3=\alpha_4-\alpha_1=C\Rightarrow \alpha_2=\alpha_3+C α2−α3=α4−α1=C⇒α2=α3+C
3️⃣ 将
α
2
=
α
3
+
C
\alpha_2=\alpha_3+C
α2=α3+C带入到
W
(
α
)
W(\alpha)
W(α)中
W
(
α
)
=
关
于
α
3
的
开
口
向
上
函
数
W(\alpha)=关于\alpha_3的开口向上函数
W(α)=关于α3的开口向上函数
从而能得到
α
3
\alpha_3
α3和
α
2
\alpha_2
α2
❓ 如何选择更新的两个变量?
选择一个 α i \alpha_i αi
误差 E i = f ( x i ) − y i E_i=f(x_i)-y_i Ei=f(xi)−yi
让 ∣ E i − E j ∣ |E_i-E_j| ∣Ei−Ej∣最大的 α j \alpha_j αj为另一个
得出来 α 1 , α 2 , α 3 , α 4 \alpha_1,\alpha_2,\alpha_3,\alpha_4 α1,α2,α3,α4则可进行下一步
例如得到
α
1
=
0
,
α
2
=
4
,
α
3
=
3
,
α
4
=
1
\alpha_1=0,\alpha_2=4,\alpha_3=3,\alpha_4=1
α1=0,α2=4,α3=3,α4=1
w
=
4
[
1
0
]
−
3
[
2
0
]
−
[
0
2
]
=
[
−
2
−
2
]
w=4\begin{bmatrix}1 \\ 0\end{bmatrix}-3\begin{bmatrix}2 \\ 0\end{bmatrix}-\begin{bmatrix}0 \\ 2\end{bmatrix}=\begin{bmatrix}-2 \\ -2\end{bmatrix}
w=4[10]−3[20]−[02]=[−2−2]
使用支持向量
x
4
x_4
x4
1
−
y
4
(
w
T
x
4
+
b
)
=
0
⇒
b
=
3
1-y_4(w^Tx_4+b)=0\Rightarrow b=3
1−y4(wTx4+b)=0⇒b=3
则有
f
(
x
)
=
w
T
x
+
b
=
[
−
2
−
2
]
x
+
3
f(x)=w^Tx+b=\begin{bmatrix}-2\\-2\end{bmatrix}x+3
f(x)=wTx+b=[−2−2]x+3
得到了
f
(
x
)
f(x)
f(x)就可以根据
x
t
e
x
t
x_{text}
xtext进行判断
SVM性质
超平面法向量是支持向量的线性组合:仅支持向量的 α i ≠ 0 \alpha_i \not= 0 αi=0
1️⃣ 鲁棒性强:SVM模型完全依赖于支持向量(SupportVectors),即使训练集里面所有非支持向量的点都被去除,重复训练过程,结果仍然会得到完全一样的模型。
2️⃣ 泛化能力强:支持向量个数通常较小,模型容易被泛化。
3️⃣ 不会出现维数灾难:对偶问题只给样本标记分配参数,而不是特征。
4️⃣ 对大规模训练样本难以实施:对偶问题的规模正比于训练样本数,在实际任务中造成很大开销
三、线性不可分SVM
松弛变量引入
SVM假定存在一个超平面能将不同类的样本完全划分开
但通常情况并非如此:因为会产生噪声(noise),异常值(outlier)

解决:通过惩罚错误分类的数目对问题建模
min
w
T
w
/
2
+
C
∗
(
#
m
i
s
t
a
k
e
s
)
\text{min}w^Tw/2+C*(\#mistakes)
minwTw/2+C∗(#mistakes)
为了使问题变得可解,引入松弛变量,使得距离间隔在加入松弛变量后满足约束条件
新的优化问题为(软-SVM):
min
w
,
b
,
ϵ
i
w
T
w
/
2
+
C
∑
i
=
1
n
ϵ
i
\underset{w,b,\epsilon_i}{\text{min}}\ w^Tw/2+C\sum^n_{i=1}\epsilon_i
w,b,ϵimin wTw/2+Ci=1∑nϵi
约束条件
w
T
x
i
+
b
+
ϵ
i
≥
+
1
(
∀
x
i
∈
+
1
)
w
T
x
i
+
b
−
ϵ
i
≤
−
1
(
∀
x
i
∈
−
1
)
ϵ
i
≥
0
(
∀
i
)
w^Tx_i+b+\epsilon_i\ge +1(\forall x_i\in +1)\\ w^Tx_i+b-\epsilon_i\le -1(\forall x_i\in -1)\\ \epsilon_i\ge0(\forall i)
wTxi+b+ϵi≥+1(∀xi∈+1)wTxi+b−ϵi≤−1(∀xi∈−1)ϵi≥0(∀i)
仍然是一个二次规划问题

模型选择——正则化常数C
C取较大值时,表示对误分类有较大的惩罚:训练误差小,但间隔也小
C取较小值时,表示对误分类的惩罚较小:训练误差大,但是间隔也大
所以需要选择一个合适的C,通常使用交叉验证法进行选择

四、SVM进阶
软分类SVM
| SVM | 软SVM | |
|---|---|---|
| 主问题 |  | 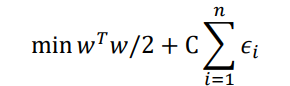 |
| 约束 |  |  |
| 对偶问题 |  | 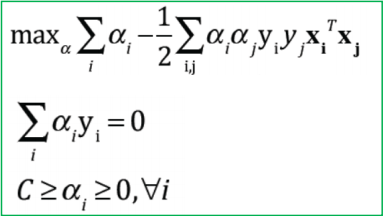 |
软-SVM的对偶问题


1️⃣ α i = 0 , μ i = 0 , ϵ i = 0 ⇒ y i ( w T x i + b ) − 1 > 0 \alpha_i=0,\mu_i=0,\epsilon_i=0\Rightarrow y_i(w^Tx_i+b)-1>0 αi=0,μi=0,ϵi=0⇒yi(wTxi+b)−1>0
2️⃣ 0 < α i < C , 0 < μ i < C , ϵ i = 0 ⇒ y i ( w T + b ) = 1 0<\alpha_i<C,0<\mu_i<C,\epsilon_i=0\Rightarrow y_i(w^T+b)=1 0<αi<C,0<μi<C,ϵi=0⇒yi(wT+b)=1
L
(
w
,
b
,
ε
i
,
α
i
,
μ
i
)
∂
L
∂
w
=
w
−
∑
i
=
1
n
α
i
y
i
x
i
=
0
∂
L
∂
b
=
−
∑
i
=
1
n
α
i
y
i
=
0
∂
L
∂
ϵ
i
=
C
−
α
i
−
μ
i
=
0
\begin{aligned} &L(w,b,ε_i,\alpha_i,\mu_i)\\ &\frac{\partial L}{\partial \pmb w}=\pmb w-\sum_{i=1}^{n}\alpha_iy_ix_i=0\\ &\frac{\partial L}{\partial b}=-\sum_{i=1}^{n}\alpha_iy_i=0\\ &\frac{\partial L}{\partial \epsilon_i}=C-\alpha_i-\mu_i=0\\ \end{aligned}
L(w,b,εi,αi,μi)∂www∂L=www−i=1∑nαiyixi=0∂b∂L=−i=1∑nαiyi=0∂ϵi∂L=C−αi−μi=0
于是有:
w
=
∑
i
=
1
n
α
i
y
i
x
i
∑
i
=
1
n
α
i
y
i
=
0
α
i
+
μ
i
=
C
\begin{aligned} & w=\sum_{i=1}^{n}\alpha_iy_ix_i\\ &\sum_{i=1}^{n}\alpha_iy_i=0\\ &\alpha_i+\mu_i=C\\ \end{aligned}
w=i=1∑nαiyixii=1∑nαiyi=0αi+μi=C
带入原朗格朗日函数可得:
L
=
1
2
∣
∣
w
∣
∣
2
+
C
∑
i
=
1
n
ϵ
i
−
∑
i
=
1
n
α
i
(
y
i
(
w
T
x
i
+
b
)
−
1
+
ϵ
i
)
−
∑
i
=
1
n
μ
i
ϵ
i
=
1
2
∣
∣
w
∣
∣
2
−
∑
i
=
1
n
α
i
(
y
i
(
w
T
x
i
+
b
)
−
1
)
+
∑
i
=
1
n
(
C
−
α
i
−
μ
i
)
ϵ
i
=
1
2
∣
∣
w
∣
∣
2
−
∑
i
=
1
n
α
i
(
y
i
w
T
x
i
−
1
)
=
∑
i
=
1
n
α
i
−
1
2
(
∑
i
=
1
n
α
i
y
i
x
i
)
T
(
∑
i
=
1
n
α
i
y
i
x
i
)
=
∑
i
=
1
n
α
i
−
1
2
∑
i
,
j
α
i
α
j
y
i
y
j
x
i
T
x
j
\begin{aligned} L&=\frac{1}{2}||\pmb w||^2+C\sum_{i=1}^n\epsilon_i-\sum_{i=1}^n\alpha_i(y_i(\pmb w^T\pmb x_i+b)-1+\epsilon_i)-\sum_{i=1}^n\mu_i\epsilon_i \\ &=\frac{1}{2}||\pmb w||^2-\sum_{i=1}^n\alpha_i(y_i(\pmb w^T\pmb x_i+b)-1)+\sum_{i=1}^n(C-\alpha_i-\mu_i)\epsilon_i \\ &=\frac{1}{2}||\pmb w||^2-\sum_{i=1}^n\alpha_i(y_i\pmb w^T\pmb x_i-1)\\ &=\sum_{i=1}^n\alpha_i-\frac{1}{2}(\sum_{i=1}^n\alpha_iy_i\pmb x_i)^T(\sum_{i=1}^n\alpha_iy_i\pmb x_i)\\ &=\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j}\alpha_i\alpha_jy_iy_j\pmb x_i^T\pmb x_j \end{aligned}\\
L=21∣∣www∣∣2+Ci=1∑nϵi−i=1∑nαi(yi(wwwTxxxi+b)−1+ϵi)−i=1∑nμiϵi=21∣∣www∣∣2−i=1∑nαi(yi(wwwTxxxi+b)−1)+i=1∑n(C−αi−μi)ϵi=21∣∣www∣∣2−i=1∑nαi(yiwwwTxxxi−1)=i=1∑nαi−21(i=1∑nαiyixxxi)T(i=1∑nαiyixxxi)=i=1∑nαi−21i,j∑αiαjyiyjxxxiTxxxj
对于约束条件有:
∀
i
,
α
i
≥
0
,
μ
i
≥
0
,
α
i
+
μ
i
=
C
∑
i
=
1
n
α
i
y
i
=
0
\forall i\ ,\alpha_i\ge 0\ ,\ \mu_i\ge0\ , \ \alpha_i+\mu_i=C\\ \sum_{i=1}^{n}\alpha_iy_i=0
∀i ,αi≥0 , μi≥0 , αi+μi=Ci=1∑nαiyi=0
可得:
C
≥
α
i
≥
0
,
∀
i
∑
i
=
1
n
α
i
y
i
=
0
C\ge\alpha_i\ge 0,\forall i\\ \sum_{i=1}^{n}\alpha_iy_i=0
C≥αi≥0,∀ii=1∑nαiyi=0
综上,软-SVM主问题的对偶问题如下:
max
α
∑
i
=
1
n
α
i
−
1
2
∑
i
,
j
α
i
α
j
y
i
y
j
x
i
T
x
j
C
≥
α
i
≥
0
,
∀
i
∑
i
=
1
n
α
i
y
i
=
0
\underset{\alpha}{\text{max}}\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j}\alpha_i\alpha_jy_iy_j\pmb x_i^T\pmb x_j\\ C\ge\alpha_i\ge 0,\forall i\\ \sum_{i=1}^{n}\alpha_iy_i=0
αmaxi=1∑nαi−21i,j∑αiαjyiyjxxxiTxxxjC≥αi≥0,∀ii=1∑nαiyi=0
软-SVM对偶问题的解中,支持向量(𝛼𝑖>0)有两类
1️⃣ 支持面上的训练样本𝜖𝑖=0:
y
i
(
x
i
⋅
w
+
b
)
=
1
0
<
α
i
<
C
y_i(\pmb x_i\cdot\pmb w+b)=1\\ 0<\alpha_i<C
yi(xxxi⋅www+b)=10<αi<C
2️⃣ 违背硬约束的训练样本𝜖𝑖>0
y
i
(
x
i
⋅
w
+
b
)
<
1
α
i
=
C
y_i(\pmb x_i\cdot\pmb w+b)<1\\ \alpha_i=C
yi(xxxi⋅www+b)<1αi=C
对于测试样本,仍然使用如下公式进行预测
y
^
=
sign
(
∑
i
∈
S
u
p
p
o
r
t
V
e
c
t
o
r
s
α
i
y
i
x
i
T
x
t
e
s
t
+
b
)
\hat y=\text{sign}(\sum_{i\in SupportVectors}\alpha_iy_ix_i^Tx_{test}+b)
y^=sign(i∈SupportVectors∑αiyixiTxtest+b)
软-SVM的高效求解
合二为一:通过惩罚错误分类的数目对问题建模
min
w
T
w
/
2
+
C
∗
(
#
m
i
s
t
a
k
e
s
)
\text{min}w^Tw/2+C*(\#mistakes)
minwTw/2+C∗(#mistakes)
等价于
min
w
T
w
/
2
+
C
∗
∑
i
=
1
n
ℓ
0
/
1
(
y
i
(
w
T
x
i
+
b
)
)
\text{min}w^Tw/2+C*\sum_{i=1}^n\ell_{0/1}(y_i(w^Tx_i+b))
minwTw/2+C∗i=1∑nℓ0/1(yi(wTxi+b))
其中, ℓ 0 / 1 \ell_{0/1} ℓ0/1是“0/1”损失函数

ℓ 0 / 1 \ell_{0/1} ℓ0/1非凸、非连续,数学性质不好。可使用如下三种替代损失
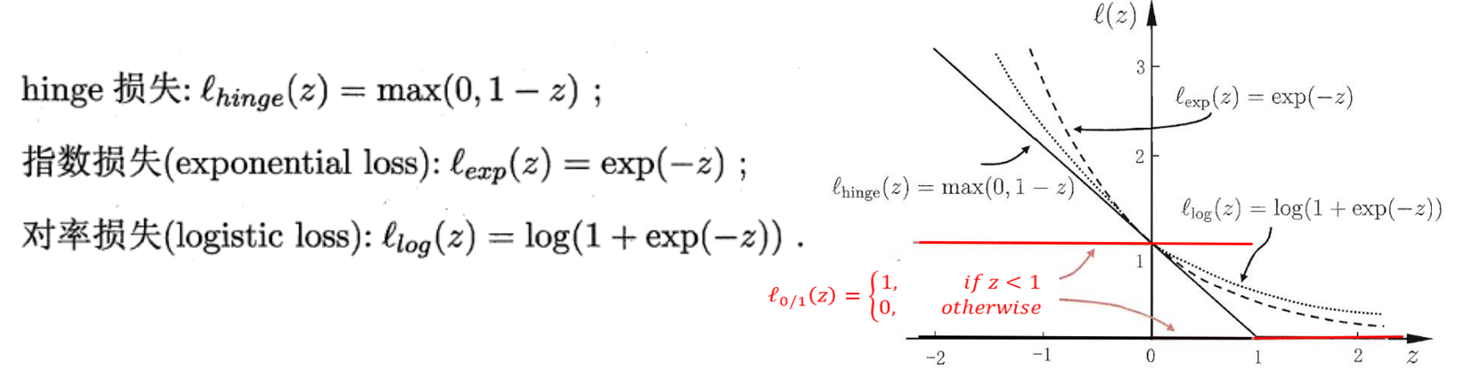
利用hinge 损失

将其写成一种“更自然”的形式
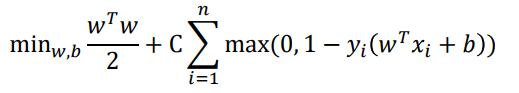
更一般形式的目标函数

使用(子)梯度下降求解目标函数
随机近似 (随机选择一个样本点)
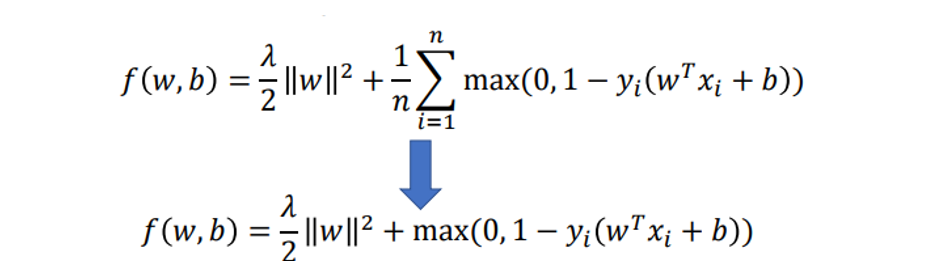
若 y i ( w T x i + b ) < 1 y_i(w^Tx_i+b)<1 yi(wTxi+b)<1:

若 y i ( w T x i + b ) ≥ 1 y_i(w^Tx_i+b)\ge 1 yi(wTxi+b)≥1:
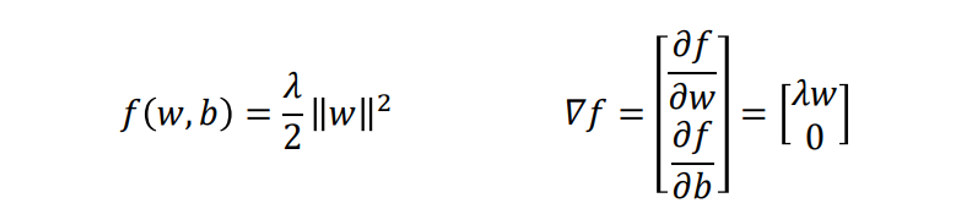
hinge loss子梯度
d
l
d
z
=
{
−
1
,
z
<
1
0
,
z
≥
0
\frac{d \mathscr{l}}{dz}=\begin{cases} -1,&z<1\\ 0,&z\ge0 \end{cases}
dzdl={−1,0,z<1z≥0
对于指数损失有:
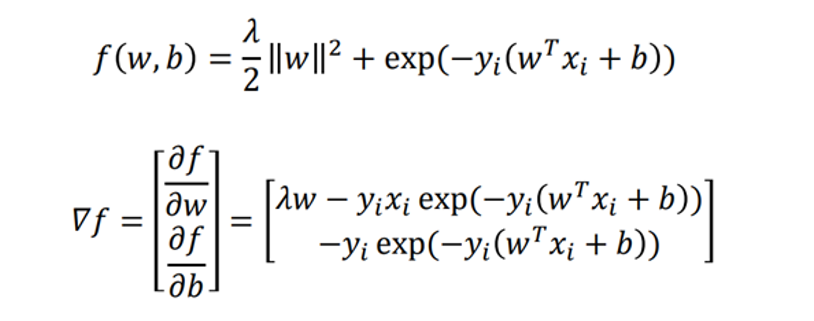
对于对率损失有:
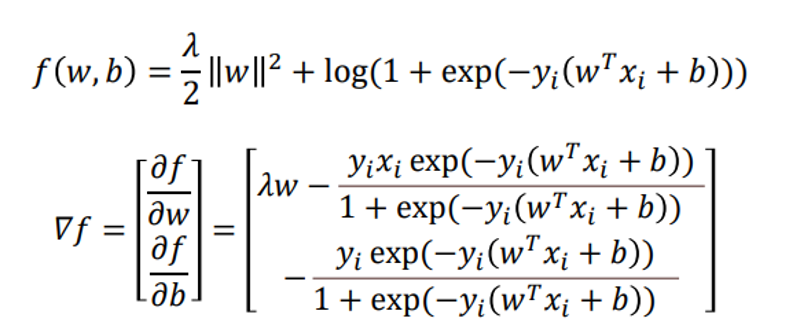
佩加索斯(Pegasos)算法

算法核心:下降步长 η t \eta_t ηt和下降方向(子梯度方向)
使用 Pegasos算法解SVM原始问题具有以下优点
简单、高效
适用于大规模训练样本问题
基于随机梯度下降,收敛速度较快,比SMO算法快很多
虽然是近似算法,但具有较高的精度
缺点:训练速度受样本向量维度影响
代码实现
SVM实现垃圾邮件分类
import numpy as np
import scipy.io
import math
def load_data():
# 读取数据
train_set = scipy.io.loadmat('./svm-data/spamTrain.mat') # 4000条
test_set = scipy.io.loadmat('./svm-data/spamTest.mat') # 1000条
train_x = np.mat(train_set['X']) # 4000*1899(每条数据是一个1899维的向量)
train_y = [] # 4000*1 代表标签
for item in train_set['y']:
if item[0] == 0:
train_y.append([-1])
else:
train_y.append([1])
train_y = np.mat(train_y)
test_x = np.mat(test_set['Xtest']) # 1000*1899
test_y = [] # 1000*1 代表标签
for item in test_set['ytest']:
if item[0] == 0:
test_y.append([-1])
else:
test_y.append([1])
test_y = np.mat(test_y)
# 源数据的标签y是1/0,需要转化成1/-1才能套用之前的公式
return train_x, train_y, test_x, test_y
def get_target_value(x_i, y_i, w, lmbda, b):
# 随机近似
max = 0 if 0 > 1-y_i*(w.T*x_i+b) else 1-y_i*(w.T*x_i+b)
value = lmbda*w.T*w/2+max
return np.array(value)[0][0]
class SVM_Pegasos:
def __init__(self, n):
# 初始化
self.w = np.zeros((n, 1)) # n*1
self.b = np.zeros((1, 1))
self.X_train, self.Y_train, self.X_test, self. Y_test = load_data()
def train_by_hinge(self, T, C, n):
"""
使用hinge损失函数
T:随机选取的数据长度
C:参数
n:向量维度
"""
X_train = self.X_train
Y_train = self.Y_train
w = self.w
b = self.b
choose = np.random.randint(low=0, high=4000, size=T)
# 产生一组长度为T的[0, 4000)随机自然数序列(有重复),用于随机挑选样本
t = 0
lmbda = 1 / (n * C)
target_function_value = []
for i in choose:
t += 1
x_i = X_train[i].T # .T表示转置
y_i = float(Y_train[i])
eta = 1.0/(lmbda*t)
constraint = y_i*(w.T*x_i+b)
if constraint < 1:
w = w - w/t + eta * y_i * x_i
b = b + eta * y_i
else:
w = w - w/t
# 求目标函数的值
value = get_target_value(x_i, y_i, w, lmbda, b)
target_function_value.append(value)
self.w = w
self.b = b
return target_function_value
def train_by_exp(self, T, C, n):
"""
使用指数损失函数
T:随机选取的数据长度
C:参数
n:向量维度
"""
X_train = self.X_train
Y_train = self.Y_train
w = self.w
b = self.b
choose = np.random.randint(low=0, high=4000, size=T)
t = 0
lmbda = 1 / (n * C)
target_function_value = []
for i in choose:
t += 1
x_i = X_train[i].T # .T表示转置
y_i = float(Y_train[i])
eta = 1.0/(lmbda*t)
constraint = -y_i*(w.T*x_i+b)
if constraint < 3: # 指数判断
partial_w = lmbda*w-y_i*x_i*math.exp(constraint)
partial_b = -y_i * math.exp(constraint)
w = w-eta*partial_w
b = b-eta*partial_b
# 求目标函数的值
value = get_target_value(x_i, y_i, w, lmbda, b)
target_function_value.append(value)
self.w = w
self.b = b
return target_function_value
def train_by_log(self, T, C, n):
"""
使用对率损失函数
T:随机选取的数据长度
C:参数
n:向量维度
"""
X_train = self.X_train
Y_train = self.Y_train
w = self.w
b = self.b
choose = np.random.randint(low=0, high=4000, size=T)
t = 0
lmbda = 1 / (n * C)
target_function_value = []
for i in choose:
t += 1
x_i = X_train[i].T # .T表示转置
y_i = float(Y_train[i])
eta = 1.0/(lmbda*t)
constraint = -y_i*(w.T*x_i+b)
if constraint < 3: # 对数判断
partial_w = lmbda*w-y_i*x_i * \
math.exp(constraint)/(1+math.exp(constraint))
partial_b = -y_i * \
math.exp(constraint)/(1+math.exp(constraint))
w = w-eta*partial_w
b = b-eta*partial_b
# 求目标函数的值
value = get_target_value(x_i, y_i, w, lmbda, b)
target_function_value.append(value)
self.w = w
self.b = b
return target_function_value
def test(self):
X_test = self.X_test
Y_test = self.Y_test
w = self.w
b = self.b
predict_result = []
for item in X_test:
y_pre = w.T*item.T+b
if y_pre[0][0] > 0:
predict_result.append(1)
else:
predict_result.append(-1)
count = 0
for i in range(len(predict_result)):
if(predict_result[i] == Y_test[i][0]):
count += 1
return count/len(predict_result)
非线性SVM
有些问题线性可分(文本分类),而有些线性不可分(图像)

在低维空间中不能线性可分的数据,在高维空间变得线性可分
对于不能在原始空间线性可分的数据
首先使用一个非线性变换z = 𝜙(𝑥)将x从低维空间映射到高维空间中(use features of features of features …);
在高维空间中使用线性 SVM 学习分类模型。
利用非线性映射把原始数据映射到高维空间中

例如:对于二维的数据
x
=
(
x
1
,
x
2
)
T
x=(x_1,x_2)^T
x=(x1,x2)T,线性SVM模型的数学表达式:
f
(
x
)
=
w
1
x
1
+
w
2
x
2
+
b
f(x)=w_1x_1+w_2x_2+b
f(x)=w1x1+w2x2+b
通过二次多项式基将 x → ϕ ( x ) = ( x 1 , x 2 , x 1 x 2 , x 1 2 , x 2 2 ) T x\rightarrow \phi(x)=(x_1,x_2,x_1x_2,x_1^2,x_2^2)^T x→ϕ(x)=(x1,x2,x1x2,x12,x22)T
参数从两个变成了5个
令新变量 z = ϕ ( x ) = ( x 1 , x 2 , x 1 x 2 , x 1 2 , x 2 2 ) T z=\phi(x)=(x_1,x_2,x_1x_2,x_1^2,x_2^2)^T z=ϕ(x)=(x1,x2,x1x2,x12,x22)T并在z形成的空间中学习SVM 模型

基于上述步骤,优化参数w 和 b 的模型为:

其对偶问题是

实际中计算量大:首先需要将𝑥映射到𝜙(𝑥) ;其次需要计算 𝑁2个 高维向量的内积 ϕ ( x i ) T ϕ ( x j ) \phi(x_i)^T\phi(x_j) ϕ(xi)Tϕ(xj),会造成维数灾难
而对偶问题的解为:
f
(
x
)
=
w
T
ϕ
(
x
)
+
b
=
∑
i
,
j
=
1
N
(
α
i
y
i
ϕ
(
x
i
)
T
)
ϕ
(
x
)
+
b
=
∑
i
,
j
=
1
N
α
i
y
i
(
ϕ
(
x
i
)
T
ϕ
(
x
)
)
+
b
f(x)=w^T\phi(x)+b=\sum_{i,j=1}^N(\alpha_iy_i\phi(x_i)^T)\phi(x)+b=\sum_{i,j=1}^N\alpha_iy_i(\phi(x_i)^T\phi(x))+b
f(x)=wTϕ(x)+b=i,j=1∑N(αiyiϕ(xi)T)ϕ(x)+b=i,j=1∑Nαiyi(ϕ(xi)Tϕ(x))+b
优化问题和解公式都是以内积形式出现
核方法
如果高维空间的内积,可以通过在原始空间获得,即
ϕ
(
x
i
)
⋅
ϕ
(
x
j
)
=
K
(
x
i
,
x
j
)
\phi(x_i)\cdot\phi(x_j)=K(x_i,x_j)
ϕ(xi)⋅ϕ(xj)=K(xi,xj)
有了核函数
K
(
x
i
,
x
j
)
K(x_i,x_j)
K(xi,xj),则不必计算高维空间的内积

既不用计算内积,又不用显示表示𝜙,没有增加计算量
举例

举例
现有5个一维数据

选择 二次多项式核: K ( x , z ) = ( x z + 1 ) 2 K(x,z)=(xz+1)^2 K(x,z)=(xz+1)2,求解 α i ( i = 1 , 2 , 3 , 4 , 5 ) \alpha_i(i=1,2,3,4,5) αi(i=1,2,3,4,5)
K ( x , z ) = ( x z + 1 ) 2 = x 2 z 3 + 2 x z + 1 = [ x z , 2 x z , 1 ] [ x z , 2 x z , 1 ] T K(x,z)=(xz+1)^2=x^2z^3+2xz+1=\begin{bmatrix}xz,\sqrt{2xz},1\end{bmatrix}\begin{bmatrix}xz,\sqrt{2xz},1\end{bmatrix}^T K(x,z)=(xz+1)2=x2z3+2xz+1=[xz,2xz,1][xz,2xz,1]T
即 ϕ ( x ) = x 2 + 2 x + 1 \phi(x)=x^2+\sqrt{2}x+1 ϕ(x)=x2+2x+1
对偶问题为:
max
∑
i
=
1
5
α
i
−
1
2
∑
i
=
1
5
∑
j
=
1
5
α
i
α
j
y
i
y
j
(
x
i
x
j
+
1
)
2
α
i
≥
0
,
∑
i
=
1
5
α
i
y
i
=
0
\max\sum_{i=1}^5\alpha_i-\frac{1}{2}\sum_{i=1}^5\sum_{j=1}^5\alpha_i\alpha_jy_iy_j(x_ix_j+1)^2\\ \alpha_i\ge0,\sum_{i=1}^5\alpha_iy_i=0
maxi=1∑5αi−21i=1∑5j=1∑5αiαjyiyj(xixj+1)2αi≥0,i=1∑5αiyi=0
通过二次规划求解,得到

支持向量为 { x 2 = 2 , x 4 = 5 , x 5 = 6 } \{x_2=2,x_4=5,x_5=6\} {x2=2,x4=5,x5=6}
判别函数即为:

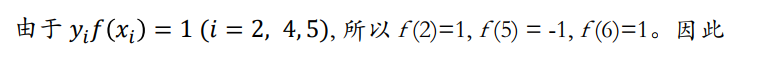


常用核函数
| 核函数 | 核函数 |
|---|---|
| 线性核 | K ( x i , x j ) = x i T x j K(x_i,x_j)=x_i^Tx_j K(xi,xj)=xiTxj |
| 多项式核 | K ( x i , x j ) = ( 1 + x i T x j ) d K(x_i,x_j)=(1+x_i^Tx_j)^d K(xi,xj)=(1+xiTxj)d |
| 高斯核 | $K(x_i,x_j)=e^{- |
| 拉普拉斯核 | $K(x_i,x_j)=e^{- |
对于非线性可分数据,若已知合适映射 𝜙(⋅) ,则可以写 出核函数K。但现实中通常不知道𝜙(⋅)
核函数的选取是SVM最棘手的地方
实际中,直接用常用核函数(高斯核,多项式核) 代入到对偶问题中,然后查看分类效果,再调整核函数的类型,这样就隐式地实现了低维到高维的映 射
借助先验知识。针对图像分类,通常使用高斯核; 针对文本分类,则通常使用线性核
核函数总结
通过非线性映射把低维向量映射到高维空间中,使向量 在高维空间中可以线性可分,以便在这个空间中构造线 性最优决策函数。
构造最优决策函数时,巧妙地利用原空间的核函数取 代了高维特征空间中的内积运算,从而避免了高维的计 算灾难。
由于实际中通常知道不知道非线性映射的具体形式,因 此“核函数选择”是核SVM的最大变数。通常使用高斯核和次数较低的多项式核
多分类SVM
将多分类问题转换为多个二分类问题
一对多法(one-versus-rest)
训练m 个分类器,如下图,学习3个二分类器
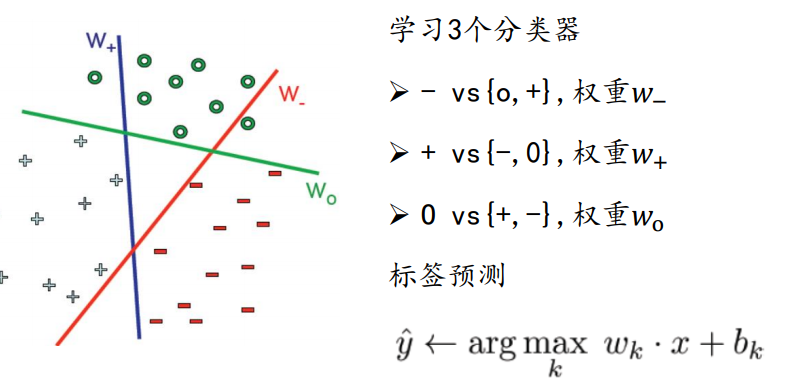
训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类,这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。
例如:假如我有四类要划分(也就是4个label),他们是A、B、C、D。
于是我在抽取训练集的时候,分别抽取
(1)A所对应的向量作为正集,B,C,D所对应的向量作为负集;
(2)B所对应的向量作为正集,A,C,D所对应的向量作为负集;
(3)C所对应的向量作为正集,A,B,D所对应的向量作为负集;
(4)D所对应的向量作为正集,A,B,C所对应的向量作为负集;
使用这四个训练集分别进行训练,然后的得到四个训练结果文件。
在测试的时候,把对应的测试向量分别利用这四个训练结果文件进行测试。最后每个测试都有一个结果 f 1 ( x ) , f 2 ( x ) , f 3 ( x ) , f 4 ( x ).于是最终的结果便是这四个值中最大的一个作为分类结果。
类别不平衡:不同类别训练样例数相差很大情况
极端情况:例如有3个正例, 997个负例,那 么分类器只需要将样本预测为负例,就能达到 99.7%的精度
改造目标函数:期望正类和负类之间的错误达到平衡

一对一法(one-versus-one )
训练 m ( m + 1 ) 2 \frac{m(m+1)}{2} 2m(m+1)个分类器

与一对多相比,看似训练分类器的数目更多。但在训练时,每个分类器仅用两个类的样例。因此训练时间成本差不多,但测试成本更大。
参考资料
[1]庞善民.西安交通大学机器学习导论2022春PPT
[2]KKT条件介绍
[3]SVM实现多分类








 本文详细介绍了支持向量机(SVM)从约束优化原理出发,探讨线性可分和不可分问题的处理,包括对偶问题、软间隔、核方法应用,以及多分类策略。通过实例演示和算法如SMO和Pegasos,深入浅出地展示了SVM的关键性质和实战技巧。
本文详细介绍了支持向量机(SVM)从约束优化原理出发,探讨线性可分和不可分问题的处理,包括对偶问题、软间隔、核方法应用,以及多分类策略。通过实例演示和算法如SMO和Pegasos,深入浅出地展示了SVM的关键性质和实战技巧。

















 653
653

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










