均方误差（Mean Squared Error, MSE，方差（Variance）、偏差的平方（Squared Bias）和误差的方差（Variance of Error）

在机器学习和统计学中，均方误差（Mean Squared Error, MSE可以分解为三个部分：方差（Variance）、偏差的平方（Squared Bias）和误差的方差（Variance of Error）。这种分解帮助我们理解模型的预测误差如何由模型的不同特性组成。

均方误差（MSE）的分解

均方误差（MSE）定义为预测值与真实值之间的平方差的期望值：
$$\text{MSE}=\mathbb{E}[(\hat{Y}-Y{)}^2]$$
其中，$\hat{Y}$ 是模型的预测值，Y 是真实值。这个误差可以分解为三部分：
$$\text{MSE}=\text{Var}(\hat{Y})+{\left(\text{Bias}(\hat{Y})\right)}^2+\text{Var}(ϵ)$$

1. 方差（Variance）：

方差衡量的是如果我们使用不同的训练集来估计模型时，预测结果的变化程度。换句话说，方差描述了模型的输出对于输入数据的敏感程度。如果方差很高，表示模型对训练数据的变化过于敏感，容易过拟合。
$$\text{Var}(\hat{Y})=\mathbb{E}[(\hat{Y}-\mathbb{E}[\hat{Y}]{)}^2]$$

2. 偏差（Bias）：

偏差表示模型预测的平均值与真实值之间的差距。偏差来源于模型对数据的近似，如果模型过于简单或者不够复杂，就可能无法正确捕捉数据的真实关系，导致较大的偏差。
$$\text{Bias}(\hat{Y})=\mathbb{E}[\hat{Y}]-Y$$
偏差的平方是对偏差的度量，其影响表现为：如果模型无法准确拟合数据的真实分布，偏差就会导致较大的误差。

3. 误差的方差（Variance of Error）：

这部分是由噪声（ϵ\epsilonϵ）引起的，即数据本身的随机性或噪声。这个项在很多情况下是无法控制的，它表示了数据中无法通过模型捕捉的部分。通常，误差的方差是给定的，并且无法通过改变模型来减少。
$$\text{Var}(ϵ)=\mathbb{E}[(ϵ{)}^2]$$
其中，ϵ 是数据中的噪声。

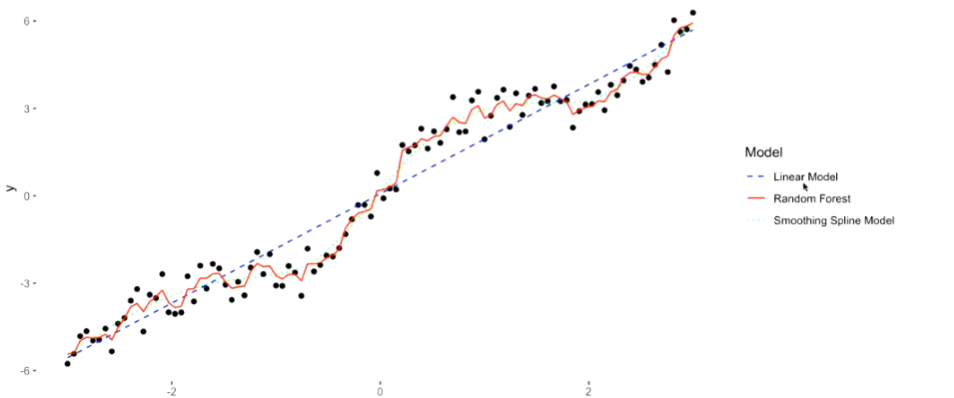
flexibility: linear < smoothing spline < random forest(high variance, low bias)