高等数学（第五章：多元微分学）

---

一、多元微分的概念

1. 二重极限

1）二重极限的概念

2）判断极限是否存在

注：若 m, n 全是偶数且 (a/m) + (b/n) ≤ 1 时，选取的路径为：y = k·x^(m-a)/b 。

① 证明极限不存在：（分子次数 ≤ 分母次数）

【方法】：

I、取直线 y = k·x^(m-a)/b ，代入，发现极限值与 k 有关（套公式）；

II、找两条极限不相等的具体的路径（找路径）。

【例题】：

• lim_x→0,y→0 (x·y) / (x²+y²)
  令 y = k·x ，有 lim_x→0,y→0 (x·k·x) / (x²+k²·x²) = k / (1+k²)
  极限取值依赖于 k 的取值，因此该极限不存在

• lim_x→0,y→0 (x·y²) / (x²+y⁴)
  令 y = k·√x ，有 lim_x→0,y→0 (x·k²·x) / (x²+k⁴·x²) = k² / (1+k⁴)
  极限取值依赖于 k 的取值，因此该极限不存在

② 证明极限存在：（分子次数 > 分母次数）

【例题】：

• lim_x→0,y→0 (x²+y²) / (|x|+|y|)
  0 ≤ (x²+y²) / (|x|+|y|) = (|x|·|x|) / (|x|+|y|) + (|y|·|y|) / (|x|+|y|) ≤ |x| + |y| → 0

• lim_x→0,y→0 [x·y²·sin(x·y)] / (x²+y⁴)
  0 ≤ |[x·y²·sin(x·y)] / (x²+y⁴)| = |(x·y²) / (x²+y⁴)| · |sin(x·y)| ≤ (1/2) · |sin(x·y)| → 0

2. 连续

二元函数连续：lim_{(x,y)→(x0,y0)} f(x, y) = f(x₀, y₀)

定义：若 lim_{(x,y)→(x0,y0)} f(x, y) = f(x₀, y₀) ，则称 f(x, y) 在点 (x₀, y₀) 处连续。

3. 偏导数

1）一阶偏导数定义

2）偏导数存在的几何意义

偏导数存在仅仅是沿着坐标轴方向趋向，如：f_x’(x₀, y₀) 是固定 y = y₀ ，而重极限存在要求是任意方向趋向，这也正是偏导数存在 --/–> 重极限存在的本质原因。

下面举一个例题：

3）高阶偏导数

下面举一个例题：

4. 可微（全微分 dz）

1）可微的定义

若函数 z = f(x, y) 在点 (x, y) 可微，且函数 z = f(x, y) 在点 (x, y) 的偏导数 ∂z/∂x , ∂z/∂y 存在，则 dz = (∂z/∂x)·dx + (∂z/∂y)·dy 。
注：只有当函数在该点可微时，全微分 dz = (∂z/∂x)·dx + (∂z/∂y)·dy 。

【注】：

2）可微的等价定义

3）可微的判定

写定义，就是取看极限是否等于 0 。

Δz = f(x, y) - f(x₀, y₀) = A·(x-x₀) + B·(y-y₀) + o(ρ)
⇒ f(x, y) - f(x₀, y₀) - A·(x-x₀) - B·(y-y₀) = o(ρ) = √[(x-x₀)²+(y-y₀)²]

其中 A = f_x’(x₀, y₀) 、B = f_y’(x₀, y₀) 。

可微的充要条件：

• 必要条件（结论推条件）：可微 ⇒ f_x’(x₀, y₀) 与 f_y’(x₀, y₀) 都存在

• 充分条件（条件推结论）：f_x’(x, y) 与 f_y’(x, y) 在 (x₀, y₀) 处连续 ⇒ 可微

下面举一个例题：

5. 偏导数连续

定义：f_x’(x₀, y₀) = lim_{x→x0,y→y0} f_x’(x, y) 且 f_y’(x₀, y₀) = lim_{x→x0,y→y0} f_y’(x, y) 。

易错：lim_x→0 f_x’(x, 0) = f_x’(0, 0) 不是偏导数连续。

6. 连续、偏导与可微的关系

详解二元之间的关系（见上图左）：

• 偏导数连续：f_x’(x₀, y₀) = lim_{x→x0,y→y0} f_x’(x, y) 且 f_y’(x₀, y₀) = lim_{x→x0,y→y0} f_y’(x, y)

• 可微：若函数在点 (x₀, y₀) 可微，则有 Δz = f(x, y) - f(x₀, y₀) = A·(x-x₀) + B·(y-y₀) + o(ρ)

• 连续：lim_{(x,y)→(x0,y0)} f(x, y) = f(x₀, y₀)

• 偏导数存在：f_x’(x₀, y₀) 与 f_y’(x₀, y₀) 存在

• 重极限存在：二重极限 lim_{(x,y)→(x0,y0)} f(x, y) 存在，要求点 (x, y) 在 D 内以任意方式趋近于点 (x₀, y₀) 时，函数 f(x) 都趋近于同一确定的常数 A ，否则该极限就不存在

【总结】：

【例题】：

类型一：

类型二：

类型三：

二、多元微分的计算

关于多元偏导符号：

• 若 x 仅为自变量，例如 z = f(x, y) ，有 ∂z/∂x = ∂f/∂x ；

• 若 x 既为自变量、也为中间变量，例如 z = f(x, u, v) 且 u = g(x) ，则 ∂z/∂x ≠ ∂f/∂x 。

1. 复合函数抽象函数求偏导

复合函数求导：

1）求具体函数的偏导数和全微分

具体的复合函数求偏导：对一个自变量求偏导，将其余自变量均看作常数，从而可利用一元函数的求导方法求解这类函数的偏导数。

方法 1：用定义（分段函数分段点，用偏导数定义求）；
方法 2：先代后求（如果是求二阶导，需要先正常求出一阶导，再去代入）。

【注】：不知道是否存在的题，先考虑利用导数定义，使用先代后求的收益并不大。

• 用定义：例如求 f_x’(a,b) 和 f_y’(a,b) ，有：
  f_x’(a,b) = lim_x→a [f(x,b)-f(a,b)] / (x-a) ;
  f_y’(a,b) = lim_y→b [f(a,y)-f(a,b)] / (y-b) 。

• 先代后求：对 x 求偏导，可以先将 y = b 代入；对 y 求偏导，可以先将 x = a 代入。
  例如：设 z = (y/x)^x/y ，求 ∂z/∂x|_(1,2) 时，可将 y = 2 代入 z ，使得 z = (2/x)^x/2 ，再对 x 求导。

例题：

2）求抽象函数的偏导数和全微分

抽象的复合函数求偏导数：若 z = f(x,y) 时，f_x’(x,y) = f₁’(x,y) ，f_y’(x,y) = f₂’(x,y) 。

3）求变上限积分的偏导数和全微分

2. 偏积分、变量替换

1）偏积分

注：对 x 作偏积分，结果中需要加 φ(y) ；对 y 作偏积分，结果中需要加 φ(x) 。

【例题】：若函数 z = f(x,y) 满足 ∂²z/∂y² = 2 ，且 f(x,1) = x+2 ，又有 f_y’(x,1) = x+1 ，则 f(x,y) = ？

【解析】：∂z/∂y = 2·y+φ(x) ，因为 f_y’(x,1) = 2+φ(x) = x+1 ⇒ φ(x) = x-1 ；
由 ∂z/∂y = 2·y+x-1 得到 z = y²+(x-1)·y+ψ(x) ，因为 f(x,1) = 1+x-1+ψ(x) = x+2 ⇒ ψ(x) = 2 ；
由上述分析可知 z = f(x,y) = y²+(x-1)·y+2 。

同类题：

• 若函数 f(x,y) 满足 f_xy’’(x,y) = 2·(y+1)·e^x ，f_x’(x,0) = (x+1)·e^x ，又有 f(0,y) = y²+2·y ，则 f(x,y) = ？
  【答案：f(x,y) = e^x·(y²+2·y+x)】

• 已知 ∂²z/∂x∂y = 1 ，且当 x = 0 时，z = siny 、当 y = 0 时，z = sinx ，则 z(x,y) = ?
  【答案：z(x,y) = x·y+sinx+siny】

2）变量代换

① 变量代换：

② 极坐标变换：

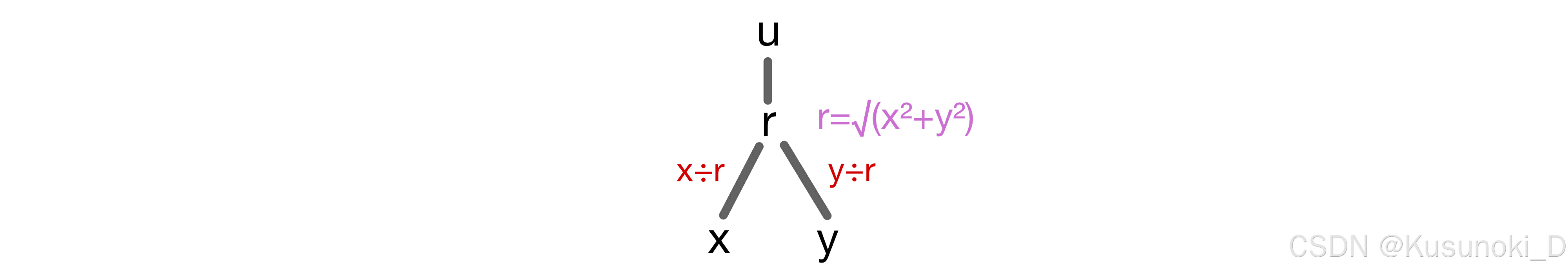
【总结】：

对微分方程作变量替换

自变量和因变量都改变的替换（对自变量和因变量都作变量替换）

3. 隐函数求偏导

1）隐函数存在定理

对于方程 F(x,y,z) = 0 ，若 F_x’ ≠ 0 ，则可以确定隐函数 x = x(y,z) ；
对于方程 F(x,y,z) = 0 ，若 F_y’ ≠ 0 ，则可以确定隐函数 y = y(x,z) ；
对于方程 F(x,y,z) = 0 ，若 F_z’ ≠ 0 ，则可以确定隐函数 z = z(x,y) 。

【做题步骤】：

• 移项、求偏导、将点带入；

• 谁的偏导不为 0 ，谁可确定隐函数。

【例题】：设方程 e^y·z + y² + z = 3 - x² ，则该方程在点 (1,-1,0) 的邻域内：可确定隐函数 x = x(y,z) 和 y = y(x,z) 。

【解析】：① 移项：e^y·z + y² + z + x² - 3 = 0 ；
② 求偏导：F_x’ = 2·x 、 F_y’ = z·e^y·z + 2·y 、F_z’ = y·e^y·z + 1 ；
③ 代点：将点 (1,-1,0) 代入偏导得到 F_x’(1,-1,0) = 2 、F_y’(1,-1,0) = -2 、F_z’(1,-1,0) = 0 ；
④ F_x’(1,-1,0) ≠ 0 且 F_y’(1,-1,0) ≠ 0 ，可确定隐函数 x = x(y,z) 和 y = y(x,z) 。

2）隐函数求导公式

① 二元隐函数的一阶偏导数计算：（公式法）

② 方程组形式的问题：

下面举几道例题：

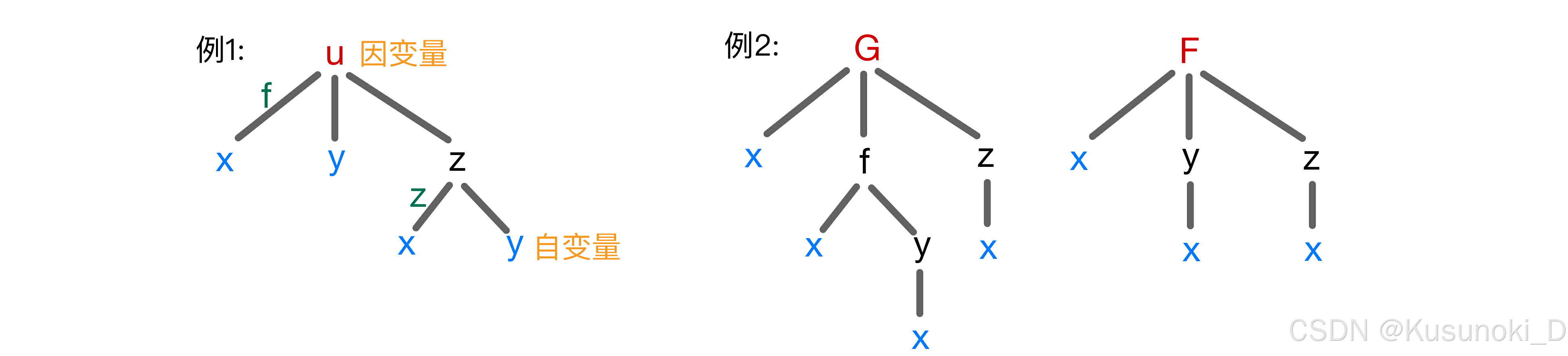
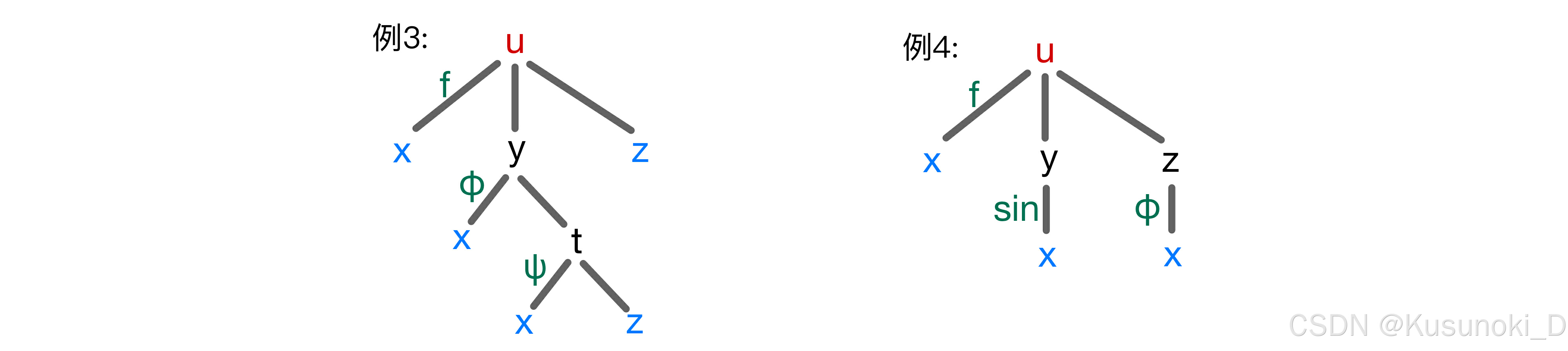
补充两道题：

【总结】：

三、无条件极值

1. 定义

设函数 z = f(x,y) 在点 P(x₀,y₀) 的某邻域内有定义，若对该去心邻域内任意的点 P(x,y) 均有 f(x,y) < f(x₀,y₀) ，则 (x₀,y₀) 为 f(x,y) 的极大值点，f(x₀,y₀) 为极大值。

总结：极值点可能在 ① 驻点（f_x’ = 0 且 f_y’ = 0）；② 不可导点。

2. 极值的充要条件

1）必要条件

设 z = f(x,y) 在点 (x₀,y₀) 处取得极值且一阶偏导数存在，则 f_x’(x₀,y₀) = 0 且 f_y’(x₀,y₀) = 0 。

2）充分条件（用于判定）

设 z = f(x,y) 在点 P(x₀,y₀) 的某邻域内有二阶连续偏导数，又 f_x’(x₀,y₀) = 0 、f_y’(x₀,y₀) = 0 。

记：A = f_xx’’(x₀,y₀) 、B = f_xy’’(x₀,y₀) 、C = f_yy’’(x₀,y₀) 。若：

• A·C - B² > 0 ⇒ 是极值（A < 0 为极大值，A > 0 为极小值）
• A·C - B² < 0 ⇒ 不是极值
• A·C - B² = 0 ⇒ 该法失效，另寻他法

3. 做题步骤

• 第一步：求偏导，解驻点；

• 第二步：求出 A、B、C ，利用 A·C - B² 进行判别。

注：在解方程中，要“放心同乘、小心同除”。例如 3x² - 6x = 0 这个式子不能写成 3x - 6 = 0 ，这样会遗弃 x = 0 这个解。

下面给出一道有关隐函数求极值的示例题：

1）选填做题技巧

看到 “极限值” + “极值” 的搭配，考虑使用保号性。

【例题】：设 z = f(x,y) 在点 (0,0) 处连续，且 lim_x→0,y→0 f(x,y)/sin(x²+y²) = -1 ，则：f(x,y) 在点 (0,0) 处取极大值。

【解析】：由 lim_x→0,y→0 f(x,y)/sin(x²+y²) 得到 f(x,y)/sin(x²+y²) < 0 且 f(0,0) = 0 ，从而得到：f(x,y) < 0 = f(0,0) ，则点 (0,0) 为极大值。

下面再给出一道选择题常考的题型：

从上题可以看出：由 ∂f/∂x > 0 可知 f(x,y) 关于 x 单增；由 ∂f/∂y < 0 可知 f(x,y) 关于 y 单减。

2）判别法失效

A·C - B² = 0 怎么办？判别法失效，用定义法。

• 选一条路径：已知 f(0,0) = 0 ，令 y = x ，有 f(x,y) = f(x,x) = -2x² ，得出点 (0,0) 不是极值（在点 (0,0) 附近可正可负）。

• 选两条路径：已知 f(0,0) = 0 ，令 y = x ，有 f(x,y) = f(x,x) = x² ；令 y = -x ，有 f(x,y) = f(x,-x) = -x² ，得出点 (0,0) 不是极值（在点 (0,0) 附近可正可负）。

• 保号性：已知 f(0,0) = 0 ，lim_x→0,y→0 f(x,y)/x² > 0 ⇒ f(x,y) > 0 = f(0,0) ，得出点 (0,0) 为极小值。

下面给出一道判别法失效的例题：（即 A·C - B² = 0）

4. 总结

利用极值定义和充分条件

四、条件极值与拉格朗日乘数法

1. 求条件极值和拉格朗日乘数法方法

求函数 z = f(x, y) 在条件 φ(x, y) = 0 下的极值

【方法】：

• 条件极值转换成无条件极值：将条件 φ(x, y) = 0 转变成 y = g(x) 这样的形式代入 f(x, y) 来消去条件；

• 但是很多情况是不好将条件变成 y = g(x) 这样的形式来消去条件，这个时候就需要利用拉格朗日乘数法。

【拉格朗日乘数法】：

【总结】：

• ① 构造拉格朗日函数 F(x,y,λ) = f(x,y) + λ·φ(x,y)；

• ② 将 F(x,y,λ) 分别对 x,y,λ 求偏导，构造方程组。

【技巧】：

• 要求 √u , ³√u（u > 0），就求 u 的最值；

• 要求 |u| ，就求 u² 的最值（因为 |u| = √(u)² ）；

• 要求 u₁·u₂·u₃（u_i > 0），就取对数（因为 ln(u₁·u₂·u₃) = lnu₁ + lnu₂ + lnu₃ ）。

2. 拉格朗日乘数法解方程

1）线代二次法

【特征】：目标和约束中出现的变量都是 “ 2 次” ，即 x² , y² , x·y , x·z , y·z 等。

【模板】：

• 第 1 步：式①·(x/2) + 式②·(y/2) = 0 ；

• 第 2 步：行列式为 0 ，求 λ 。

下面给出一道例题：

2）方程组讨论法

【方法】：通过 ① 式和 ② 式得到 x 与 y 之间的关系，再代入式 ③ 。

下面给出一道例题：

3）参数方程法

五、有界闭区域最值

连续函数在有界闭区域上的最值一般求法：

1. 方法

【理论总结】：

设 z = f(x,y) 在平面有界闭区域 D 上连续，则 f(x,y) 在 D 存在最大值 M 和最小值 m 。因次，能够取得最值的点可能是在 D 内满足 ∂f/∂x = 0 ，∂f/∂y = 0 ；可能是偏导数不存在的点；也可能是 D 的边界点上达到。

【求解步骤】：

• 求 f(x,y) 在 D 内可能取得极值（驻点和一阶偏导数不存在的点）的函数值。
  ① 求导；② 找可疑点（f_x’=0 , f_y’=0 和导数不存在的点）；③ 验证是否在边界内。

• 求 f(x,y) 在 D 的边界上的最大、最小值。
  ① 拉格朗日乘数法；
  ② 化为参数方程（圆、椭圆），适用于 x² , y² , x+y , 2·x ，没有交叉项 x·y 时；
  ③ 消去变量化为一元（三角形、矩形、圆）

• 将上面各函数值进行比较。

【题目类型】：边界为三角形、矩形 or 边界为圆、椭圆 。

2. 边界为三角形、矩形

求解方法一般为：① 消去变量化为一元；② 拉格朗日乘数法。

化为一元时，一定要标注 x 的范围！
需要代值的点有：驻点和端点。

3. 边界为圆、椭圆

求解方法一般为：① 消去变量化为一元；② 化为参数方程（无交叉项时）；③ 拉格朗日乘数法。

椭圆方程为：x²/a² + y²/b² = 1 ，化为参数方程时，为 x = a·cosθ 、y = b·sinθ 。