记余弦定理在实际工程计算中的一个典型案例（附加C++代码）

如图，这是地球🌏的竖剖面，向上为北极方向。黑点为地表上的某一测控站，红白二点表示同一海拔高度的两个空间目标。理想情况下，测控站向北延俯仰角为零看去刚好能观测到白点，显然，“白点-地心-黑点”所成的夹角是容易计算的。然而，由于山脉，树木等的遮挡，测控设备往往存在一个遮蔽角，即“白点-黑点-红点”夹角。此时，如何计算“红点-地心-黑点”夹角？这个问题可以归纳为纯几何问题，即——已知钝角三角形的钝角及其对边和另外任意一个边，求已知的这两个边的夹角。

犹记得，当年参加高考，刚拿到数学试卷，翻过来扫视一眼，马上就看到了一个大题——请证明余弦定理！比较庆幸的是高考前一个月，我们数学老师刚好在课堂上讲过用几何法证明余弦定理，所以这道题也帮助本人成功考上大学。为什么要说这个小故事呢？因为上面提出的问题正是用余弦定理解决工程问题的经典案例。下面详细介绍其原理和算法：

首先，什么是余弦定理？对于任意三角形，有以下表达式：

 

其次，定义“红点-地心”为边a, “黑点-地心”为边b，“红点-黑点”为边c，要计算的“红点-地心-黑点”夹角为γ。

将已知变量带入余弦定理，即公式（1），可以得到一个一元二次方程，这个方程的二次项系数、一次项系数、常数项分别为：

A = 1

B = -2b*cos(α)

C = b*b - a*a

注意，这里α为遮蔽角+90度。

然后，用求根公式计算边c：

 

显然，应该舍弃永远为负值的那个解，所以边c的唯一解为： 

既然已经知道了三角形的三个边长，那么带入余弦定理公式（3），即可求出“红点-地心-黑点”夹角γ。

C++代码实现如下：

#include <iostream>
#include <cmath>
using namespace std;

#define PI 3.1415926535897932384626433832795
#define DEG2RAD(x) ((x)/180.0*PI)
#define RAD2DEG(x) ((x)/PI*180.0)

//已知钝角三角形的钝角及其对边和另外任意一个边，求已知的这两个边的夹角
double CalAngle(double aLine, double bLine, double alphaDeg)
{
	//根据余弦定理求边长c
	double a = 1; //二元一次方程的系数
	double alphaRad = DEG2RAD(alphaDeg);
	double b = cos(alphaRad) * (-2) * bLine;  //二元一次方程的系数
	double c = bLine * bLine - aLine * aLine;  //二元一次方程的系数

	double tmp = sqrt(b * b - 4 * a * c);
	double x1 = ((-1 * b) + tmp) / (2 * a);
	//double x2 = ((-1 * b) - tmp) / (2 * a); //x2必然未负值，所以舍弃
	double cLine = x1;
	double gammaRad = acos((aLine * aLine + bLine * bLine - cLine * cLine) / (2 * aLine * bLine));
	double gammaDeg = RAD2DEG(gammaRad);
	return gammaDeg;
}

int main()
{
	double gamma = CalAngle(36371, 6371, 105);
	cout << "gamma = " << gamma << endl;
}

运行结果如下：

 为了验证该算法的正确性，用matlab输入三角形三个边长，计算三个角度，代码如下：

clear all;
a = 36371; b = 6371; c = 34197.667473781417;

A = acosd((b^2 + c^2 - a^2) / (2 * b * c));
B = acosd((c^2 + a^2 - b^2) / (2 * c * a));
C = acosd((a^2 + b^2 - c^2) / (2 * a * b));

disp(['A = ', num2str(A)]); disp(['B = ', num2str(B)]); disp(['C = ', num2str(C)]);

结果如下： 

 

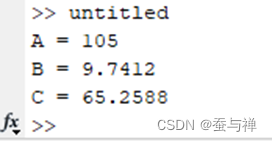
 总结：已知钝角三角形的钝角及其对边和另外任意一个边，求已知的这两个边的夹角。解决这个问题的核心思路是调用两次余弦定理公式，先通过解一元二次方程把第三个边长计算出来，再计算夹角。