@[TOC](文章预览:)
#1.直线趋势
#1.1定义
直线趋势法又称直线趋势预测法、线性趋势预测法,是对观察期的时间序列数据表现为接近一条直线,表现为近似值的上升和下降时采用的一种预测方法。
#1.2模型:
![]()
#1.3适用条件
直线趋势法满足且特点是一阶差分约为一个常数。
#1.4参数估计
利用最小二乘法对模型进行![]() 与
与![]() 的参数估计:
的参数估计:
目标: ![]()
对![]() 求偏导:
求偏导:
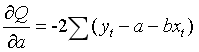
令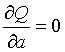 既:
既:
![]()
化简得:
![]()
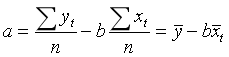
对![]() 求偏导:
求偏导:

令 即:
即:
![]()
![]()
![]()
若以时间序列中的中点为时间原点(对时间进行编号),即![]() 满足,可化简为下式:
满足,可化简为下式:
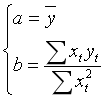
#1.5编号方法
编号方法:
如果时间序列有偶数项,则对称编号方式:
… , −5, −3,−1, 1, 3, 5, …
·如果时间序列有奇数项,则对称编号方式:
… , −2, −1, 0, 1, 2, …
#1.6实例
计算序列的一阶差分,列于表中,从计算结果可以看出,一阶差分大体接近。因此,可配合直线趋势模型来预测。

代入公式,解得:

所求直线预测模型为:
![]()
#2指数曲线法
#2.1定义
#2.3模型
![]()
上式中𝑎、𝑏为参数;𝑡为时间。
图像如下图:
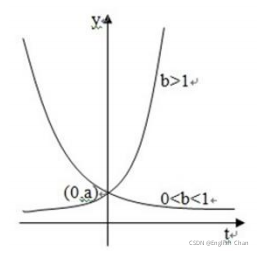
#2.4适用条件

#2.5参数估计
两边取对数,可以化成直线模型:
![]()
由上式观测可得知对数的一阶差分为一个常数,即:
![]()
同样的,可以用最小二乘法对式子![]() 进行与的参数估计:
进行与的参数估计:
![]()
要使上式目标取最小,对分别对![]() 与
与![]() 求偏导,令偏导等于0
求偏导,令偏导等于0
对![]() 求偏导:
求偏导:
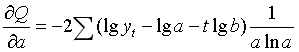
令 即:
即:
![]()
化简得:
![]() ①
①
对![]() 求偏导:
求偏导:

令 即:
即:
![]()
化简得:
![]() ②
②
合并①②式:
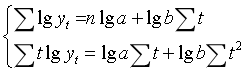
若以时间序列中的中点为时间原点,即满足![]() ,可化简为下式:
,可化简为下式:

再对其取反对数,即可估计出参数![]() 与
与![]()
#2.6实例
某市居民储蓄存款余额资料如下表所示,试预测2000年该市居民储蓄存款余额

分析:从结果可以看出,环比发展速度大体上接近,因此,可以配合 指数曲线预测模型进行预测。

求反对数得:
![]()
则指数曲线预测模型为:
![]()
将代入预测模型,可得2000年该市居民储蓄存款余额的预测值为:
![]()
#3修正指数曲线法
#3.1定义
采用指数曲线外推预测,存在预测随着时间推移无限增大的问题。这导致与客观事实是不一致的,因为任何事物的发展都有其一定的限度,不可能无限增长。例如,商品的销售量,在其市场成长期内可能会按照指数曲线增长,但随着时间的推移,其增长的趋势可能会减缓以至于停滞。对于这种情况,可以考虑改用修正指数曲线进行预测。
#3.2模型
![]()
其中k值表示对指数曲线模型进行某种修正
#3.3适用条件
由指数的一阶差分:
![]()
则一阶差分的环比

所以修正指数曲线预测模型的特征为一阶差分的环比为一个常数
#3.4图像
一阶导数决定函数的单调性性、二阶导数决定函数的凹凸性可得:
当k>0、 a<1、0<b<1时,![]() ,可得函数是一个单调递增且是一个凹函数。
,可得函数是一个单调递增且是一个凹函数。![]() 时
时![]() ,且
,且![]() 时,
时,![]() ,可知
,可知![]() 是一条渐近线。由上述可分析
是一条渐近线。由上述可分析![]() 会随着
会随着![]() 的增长从快到慢,最后不断接近
的增长从快到慢,最后不断接近![]() ,图像如下图:
,图像如下图:

同理其他情况也可以得出各种情况图像如下:

#3.5参数估计
由于修正指数模型过于复杂,所以不使用最小二乘法进行估计,而是用三段法。
设有![]()
![]()
将序列![]() 分成三段,每段有个数据,对各段分别求和,即:
分成三段,每段有个数据,对各段分别求和,即:


由![]() 再开
再开![]() 次方得:
次方得:

由④得:

由①得:

#3.6实例
某市居民存款余额最小二乘法计算表(单位:亿元)


求反对数得到:
![]()
则指数曲线预测模型为:
![]()
将各年的t值代入预测模型,可求得历年追溯预测值![]() 。
。
![]()
#4生长曲线
#4.1龚伯兹曲线
#4.1.1定义
龚伯兹曲线,是美国统计学家和数学家龚伯兹首先提出用作控制人口增长率的一种数学模型,50%随后被广泛应用于新产品的研制发展、成熟和衰退分析。工业产品寿命一般可分为四个时期:引入期、成长期、成熟期和衰退期。龚伯兹曲线特别适用于对处在成熟期的商品进行预测。
#4.1.2模型
龚伯兹曲线预测模型为:
![]()
上式中,k为待定参数,t为时间。 a、b的不同取值决定龚伯兹曲线的不同形式,用以描述不同产品生命周期的具体规律。
#4.1.3适用条件
其对数一阶差分的环比为一常数
#4.1.4图像
对模型进行一阶导数:
![]()
对模型进行二阶导数:

最终可求得曲线拐点的位置为:

根据![]() 取值的不同所得图像有以下四种
取值的不同所得图像有以下四种
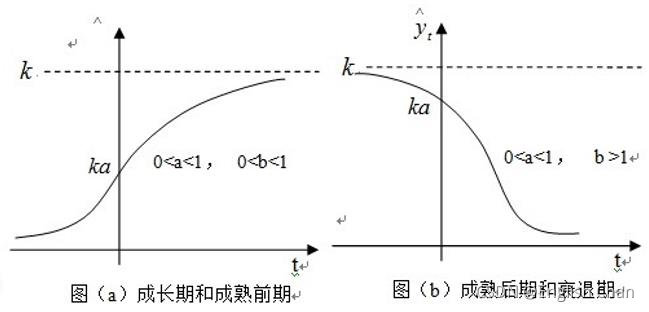

#4.1.5参数估计
为了确定模型中的参数,通常把模型改写为对数形式:
![]()
由于龚伯兹曲线的对数形式为修正指数曲线模型:![]()
因而根据修正指 数曲线预测模型的特点,可知龚伯兹曲线预测模型的特征是,其对 数一阶差分的环比为一常数。因此,当时间序列 𝑦𝑡 的对数一阶差 分的环比近似一常数时,可配合龚伯兹曲线预测模型来预测。
同理由于它在形式上与修正指数曲线模型相同。因此可以用修正指数曲线估计参数的方法,利用三段法求得参数k、a、b:



#4.1.6实例
已知某品牌平板电脑在甲地2005~2013年销售额如表所示,试预测2014年和2015年的销售额各为多少万元。
甲地某平板电脑2005~2013年销售额龚伯兹曲线预测计算表(单位:万元)

根据散点图,曲线的变化趋势是接近于一个S型的曲线,为了进一步确定合适的预测模型,需要计算序列数据的对数一阶差分及其环比指数,我们观察环比指数,除2007年和2011年,其他指数大体接近,因此可用龚伯兹曲线进行预测



![]()
#4.2罗吉斯蒂曲线
#4.2.1定义
罗吉斯蒂曲线又称逻辑曲线,是最早由比利时生物数学家维哈尔斯特(P. F. Verhulst)于1838年为研究人口增长过程而导出,但直至20世纪20年代才被美国生物学家及人口统计学家皮尔(R.Pearl)和里德(L. J. Reed)重新发现并应用于生物繁殖和生长过程。所以罗吉斯蒂曲线又通常被称为皮尔生长曲线(Pearl-ReedGrowth Curve),简称皮尔曲线(Pearl-Reed Curve),目前该曲线已被广泛应用于多领域的模拟研究。
#4.2.2模型

#4.2.3适用条件
根据修正指数曲线预测模型的特点,可知罗吉斯蒂曲线预测模型的特征是其倒数一阶差分的环比为一常数。因此,它适用于历史数据取倒数后的一阶差分环比较接近的预测对象。
#4.2.4图像
对模型求一、二阶导数,有:

令二阶导数等于0,可求得曲线拐点的位置为:

曲线拐点左侧呈上凹趋势,过了该拐点后曲线变为向下凹趋势。

#4.2.4参数估计
由于罗吉斯蒂曲线的倒数是修正指数曲线,因此仿照修正指数曲线估计参数的方法可得的![]() 计算公式
计算公式


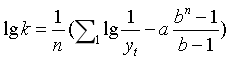
#4.2.5实例
我国1990~2001年私人汽车拥有量资料如表5-4所示,试采用罗吉斯蒂曲线模型对我国2004年私人汽车拥有量进行预测。
1990~2001年私人汽车拥有量罗吉斯蒂曲线计算表 (单位:万辆)


于是建立罗吉斯蒂曲线预测模型为:
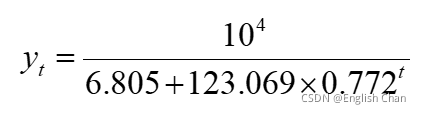
将各年的t值代入预测模型,可得各年的追溯预测值![]() 。最后, 用已建立的模型预测我国2004年私人汽车拥有量为:
。最后, 用已建立的模型预测我国2004年私人汽车拥有量为:
























 290
290

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








