互易对称性
若有 f ( t ) ↔ F ( j w ) f(t) ↔ F(jw) f(t)↔F(jw) , 则有 F ( t ) ↔ 2 π f ( − w ) F(t) ↔ 2πf(-w) F(t)↔2πf(−w)
若有 f ( t ) f(t) f(t) 是偶函数 , 则有 F ( t ) ↔ 2 π f ( w ) F(t) ↔ 2πf(w) F(t)↔2πf(w)
例子1: 求出H(w)=δ(w) 的傅里叶逆变化
解: 已知
δ
(
t
)
↔
1
δ(t) ↔ 1
δ(t)↔1
则有：
1
↔
2
π
δ
(
w
)
1 ↔ 2πδ(w)
1↔2πδ(w)
1
2
π
↔
δ
(
w
)
\frac{1}{2π} ↔ δ(w)
2π1↔δ(w)
例子2: 求出H(w)为门函数的傅里叶逆变化
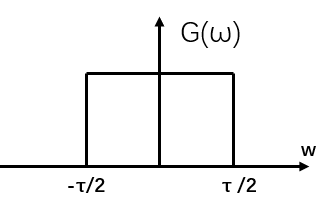
解： 已知门函数的傅里叶变化为Sa(w)函数：
因为：
g
(
t
)
↔
τ
S
a
(
w
τ
2
)
g(t) ↔ τSa(w\frac{τ}{2})
g(t)↔τSa(w2τ)
所以： τ S a ( t τ 2 ) ↔ 2 π G ( w ) τSa(t\frac{τ}{2})↔2πG(w) τSa(t2τ)↔2πG(w)
τ 2 π S a ( t τ 2 ) ↔ G ( w ) \frac{τ}{2π}Sa(t\frac{τ}{2})↔G(w) 2πτSa(t2τ)↔G(w)
扫一扫
4282
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
