【离散数学】 SEU - 28 - 2021/06/11 - Lattice and Boolean Algebra

Discrete Mathematical Structures (6th Edition)
2021/06/09 - Lattice and Boolean Algebra

---

Lattice and Boolean Algebra

Lattice

Homomorphism

Distributive Lattice

Distributive Lattice: $<L,\wedge ,\vee >$ is a lattice, $\forall a,b,c\in L$
$a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c)$
$a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c)$

Note: Actually, distributive lattice only needs to satisfy one of them.

Dimond lattice (not distributive lattice)

Pentagon lattice (not distributive lattice)

Theorem: A lattice $L$ is nondistributive if and only if it contains a sublattice that is isomorphic to the diamond lattice or the pentagon lattice.

Greatest (Least) Element

The greatest (least) element $a$：Given lattice $<L,\preccurlyeq >$, for any $b$, we have $b\preccurlyeq a(a\preccurlyeq b)$

The greatest (least) element of a lattice is unique, if it exists.
Denoted as $1(0)$.

Bounded lattice $<L,\preccurlyeq >$: $<L,\preccurlyeq >$ is a lattice and it has the greatest and least elements.
Denoted as $<L,\wedge ,\vee ,1,0>$.

Complement element

Definition: $<L,\wedge ,\vee ,0,1>$ is a bounded lattice, $a\in L$, if there exists $b\in L$
$$a\wedge b=0，a\vee b=1$$
$b$ is the complement element of $a$, denoted as $a^{\prime }$.

Definition: $<L,\wedge ,\vee ,1,0>$ is a bounded lattice, if for any $a\in L$, $a$ has a complement element $a^{\prime }$, then $L$ is a complemented lattice.

Theorem: $<L,\wedge ,\vee ,0,1>$ is bounded and distributive. If $a\in L$ and $a$ has its complement element $b$, then $b$ is the unique complement element of $a$.

Review

Boolean Algebra

Definition: A Boolean algebra is a lattice that is distributive and complemented.

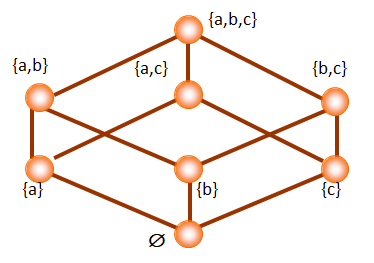
Example: $<P(A),\cup ,\cap ,\sim ,\varnothing ,A>$ is a Boolean algebra.

Theorem: In Boolean Algebra $B$, $a,b\in B$, if $a\preccurlyeq b$, then we have:
(1) $a\wedge b’=0$
(2) $a’\vee b=1$

Properties

Theorem: Given $<B,\wedge ,\vee {,}^{\prime },0,1>$
(1) For every $a\in B$, we have $(a^{\prime }{)}^{\prime }=a$
(2) For every $a,b\in B$, a and b have complements $a^{\prime },b^{\prime }$, then
$(a\wedge b{)}^{\prime }=a^{\prime }\vee b^{\prime },(a\vee b{)}^{\prime }=a^{\prime }\wedge b^{\prime }$

Theorem: $<B,\wedge ,\vee {,}^{\prime },0,1>$ is a Boolean algebra, the following laws hold:
(1) $a\wedge b=b\wedge a,a\vee b=b\vee a$
(2) $(a\wedge b)\wedge c=a\wedge (b\wedge c),(a\vee b)\vee c=a\vee (b\vee c)$
(3) $a\wedge a=a,a\vee a=a$
(4) $a\wedge (a\vee b)=a,a\vee (a\wedge b)=a$
(5) $a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c),a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c)$
(6) $a\vee 0=a,a\wedge 1=a$
(7) $a\vee 1=1,a\wedge 0=0$
(8) $a\vee a^{\prime }=1,a\wedge a^{\prime }=0$
(9) $a=a^{\prime \prime }$
(10) $(a\vee b{)}^{\prime }=a^{\prime }\wedge b^{\prime };(a\wedge b{)}^{\prime }=a^{\prime }\vee b^{\prime }$

Another Definition

$<B,\ast ,\oplus >$ is an algebraic system, if $\forall a,b,c\in B$ the following conditions hold
$$\text{H1: }a\ast b=b\ast a,a\oplus b=b\oplus a\text{\hspace{1em}(Commutative Laws)}$$
$$\text{H2: }a\ast (b\oplus c)=a\ast b\oplus a\ast c,a\oplus (b\ast c)=(a\oplus b)\ast (a\oplus c)\text{\hspace{1em}(Distributive Laws)}$$
$$\text{H3: for 0 and 1 in }B,\forall a\in B,a\ast 1=a,a\oplus 0=a\text{\hspace{1em}(Identity Laws)}$$
$$H4:\forall a\in B\text{, there exists }{a}^{\prime }\in B,s.t.a\oplus a^{\prime }=1,a\ast a^{\prime }=0\text{\hspace{1em}(Complementation Laws)}$$
then $<B,\ast ,\oplus ,0,1>$ is a Boolean algebra.

Sub-Boolean Algebra

Sub-Boolean algebra $H$: $<B,\wedge ,\vee {,}^{\prime },0,1>$ is an algebra
$H$ is a subset of $B$,
$H$ contains $0$ and $1$,
$H$ is closed w.r.t. $\wedge ,\vee {,}^{\prime }$

Homomorphism

Homomorphism $f$: $<B,\wedge ,\vee {,}^{\prime },0,1>$ and $<B,\oplus ,\otimes ,\overline{0},\alpha ,\beta >$ are two Boolean algebra. $f$ is a mapping from $B$ to $B^{\prime }$, satisfying

• $f(a+b)=f(a)\oplus f(b)$
• $f(a\cdot b)=f(a)\otimes f(b)$
• $f(a^{\prime })=\overline{f(a)}$
• $f(0)=\alpha ,f(1)=\beta$

Atom

$a$ covers $b$: $b\le a$ and $b\ne a$, there is no other element $c$，such that $b<c$ and $c<a$.
Atom: $<B,\wedge ,\vee {,}^{\prime },0,1>$ is a Boolean algebra，if $a\in B$ and $a$ covers $0$，then $a$ is an atom of $B$.

---

ALL RIGHTS RESERVED © 2021 Teddy van Jerry
This blog is licensed under the CC 4.0 Licence.

---

See also

Teddy van Jerry’s Personal Homepage
Teddy van Jerry’s CSDN Homepage
Teddy van Jerry’s GitHub Homepage