移动机器人视觉伺服轨迹跟踪控制论文复现 1

移动机器人视觉伺服轨迹跟踪控制论文复现 1

1.1 论文名称

《Visual Servoing Trajectory Tracking and Depth Identification for Mobile Robots With Velocity Saturation Constraints》发表于IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS期刊。

1.2 研究背景

与一般的轨迹跟踪任务不同，这里讨论的视觉伺服跟踪应用于一组给定的视频帧来表示期望的轨迹，并在线反馈视觉信息来表示移动机器人的实时定位。在开发轨迹跟踪控制器时，必须考虑由于视觉传感器不确定性引入的问题，如相机的视场角(FOV)，未知场景的深度。特别是单目视觉移动机器人系统，由于目标与机器人的相对位姿是根据二维图像估计得到的，场景深度信息一般无法获取。因此，基于该视觉系统的机器人模型不可避免地包含未知深度参数。视觉伺服轨迹跟踪的另一类挑战来自于移动机器人本身，其中非完整约束和速度饱和约束是两个重要的方面。特别地，由于机器人执行机构的物理限制，速度饱和是一种常见的现象，在追求快速响应时，产生的速度指令可能会超过执行器能力，导致系统性能下降，跟踪效果变差，甚至导致系统不稳定。尽管一些移动机器人的纯跟踪控制器能够很好地处理速度饱和问题，但耦合视觉不确定性时，这些控制器生成的速度指令的边界无法明确确定。因此，对于视觉伺服轨迹跟踪任务，在视觉相关参数未知的情况下，保证速度输入满足饱和约束仍然是一个具有挑战性的问题。这篇文章重点研究了移动机器人视觉伺服任务中耦合未知深度的速度输入饱和问题。

1.3 思路与贡献

在这篇文章中，针对具有速度饱和约束的移动机器人，提出了一种视觉伺服轨迹跟踪方法，能够在视觉伺服过程中同时实现深度辨识。具体地，利用单应性矩阵分解技术，得到缩放的平移误差和方向误差，从而构建非完整移动机器人的视觉跟踪误差模型。采用饱和函数来设计视觉伺服控制律，保证生成的速度指令在饱和限制内，其中提出一种自适应更新律来处理未知深度。而且，自适应更新律满足PE条件，未知深度能够在视觉伺服过程中进行辨识。此外，分析了所设计的速度控制器的有界性，并提供了相应参数的选择规则。最后，基于Lyapunov的稳定性分析表明视觉伺服轨迹误差渐进收敛于零。这篇文章的主要贡献：
（1）针对图像深度未知的非完整移动机器人，提出了一种满足速度饱和约束的自适应视觉伺服轨迹跟踪控制器。虽然控制律与未知深度耦合，但速度指令的有界性仍可明确确定。
（2）不仅可以在线自适应地更新未知深度，而且可以在视觉伺服过程中同时辨识。
（3）与现有的仅实现一致最终有界的饱和控制器相比，在同时存在饱和约束和未知深度的情况下，理论上实现了渐近稳定性，通过对比实验也验证了其实际有效性。

1.4 系统模型构建

下图是在视觉伺服跟踪任务中的坐标系，其中单目相机坐标系与机器人坐标系重合。令$F^{\ast }$表示全局参考位姿，$F_C$表示当前实际机器人位姿。$x^c$表示机器人航向，与相机光轴平行。$y^c$表示与车轮轴平行，$z^c$表示垂直于纸面向外。相应地，$F^D$表示在给定的机器人理想轨迹中当前理想位姿。而且$\theta \in (-\pi ,\pi ]$和${\theta }_d\in (-\pi ,\pi ]$分别是$F_C$和$F^D$相对于$F^{\ast }$的旋转角度。

不失一般性，假设一组至少4个同平面但不共线的静态特征点$P$位于平面$\pi$。此外，$d^{\ast }\in {\mathbb{R}}^{+}$是一个未知常数，表示$F^{\ast }$原点与平面$\pi$的距离。在视觉伺服跟踪任务中，坐标系$F^{\ast }$相对于平面$\pi$是静止的。
假设在参考坐标系$F^{\ast }$下$F_C$的坐标是$P(t)={\left[\begin{array}{ccc}x(t)& y(t)& z(t)\end{array}\right]}^T$。当移动机器人移动时，$F_C$的位姿相对于$F^{\ast }$产生相应的变化。就移动机器人运动学模型而言，其运动学公式如下所示：

由于机器人的实际速度受限于电机转矩，即

同样地，假设在参考坐标系$F^{\ast }$下$F_D$的坐标是$P_d(t)={\left[\begin{array}{ccc}{x}_d(t)& y_d(t)& z_d(t)\end{array}\right]}^T$。其运动学公式如下所示：

对于视觉伺服任务，期望地机器人轨迹表示为在预先给定的图像序列(如视频)，其中包含特征点集$P$。
视觉伺服跟踪控制的目标是在受到速度饱和限制的条件下，使当前的移动机器人位姿$F_C$与$F_D$重合。具体来说，机器人的实时位姿$F_C$是通过反馈的特征点图像获得的。由于只能记录2-D图像，所估计的位姿缺乏缩放信息。在这篇文章中，使用单应性矩阵分解方法来估计机器人的实时位姿。利用这个方法，计算相对于$F^{\ast }$的缩放位姿$F_C$如下：

同样地，根据给定的期望图像序列，在期望轨迹上的期望位姿$F_D$也可以计算如下：.

注意，由于$d^{\ast }$是未知的，因此从给定的期望图像序列中无法获得期望轨迹$v_d$的实际线速度。通过单应性矩阵分解方法得到缩放期望位姿后，滤波得到的期望位姿序列可以进一步估计每个时刻对应的缩放期望线速度$v_d^{\ast }$和角速度${\omega }_d$，其中$v_d^{\ast }=\frac{v_d}{d^{\ast }}$。结合式( 5 )，期望轨迹运动学可改写为：

轨迹跟踪误差可定义如下：

式中：$e_x=\frac{x_e}{d^{\ast }}$和$e_y=\frac{y_e}{d^{\ast }}$为缩放后的平移误差，$x_e$和$y_e$为欧氏空间中的真实平移误差，如上图所示。而对于旋转误差，有$e_{\theta }={\theta }_e$。显然，当$e_x$，$e_y$，$e_{\theta }$收敛到零时，$x_e$，$y_e$，${\theta }_e$也收敛到零，这意味着移动机器人成功地跟踪了期望的轨迹。对上式取时间导数可得

1.5 控制器设计

所提方法的闭环控制框图如下图所示。整个控制模块由速度饱和控制器和未知深度$d^{\ast }$的自适应更新律组成。此外，自适应更新律还可以在视觉伺服跟踪过程中实现深度辨识。

考虑跟踪误差模型，受李雅普诺夫控制设计方法的启发，线速度和角速度控制器可设计为

式中：$k1，k2，k3\in R^{+}$为正控制参数。该控制器的一个显著特点是引入了饱和函数$tanh(\cdot )$来重塑跟踪误差。由于$tanh(\cdot )\in [-1,1]$，生成的速度命令可以在一定的限制值内巧妙地设计。对于未知深度$d^{\ast }$的估计，设计自适应更新律为
式中：$\Gamma \in R^{+}$为正更新增益。$Projd(\cdot )$是一个投影函数，定义如下

其中$d_{\min }\in {\mathbb{R}}^{+}$和$d_{\max }\in {\mathbb{R}}^{+}$分别是未知深度的正下界和正上界。

1.6 论文的实验结果

实验A：对比追踪结果。在本实验中，机器人将跟踪一条蛇形运动轨迹。为了客观地比较所提出的方法与文献“Visual Servo Tracking of Wheeled Mobile Robots With Unknown Extrinsic Parameters”中的方法，设定机器人的初始位姿误差完全相同。下图从上到下的顺序依次表示移动机器人在跟踪期望轨迹时的位姿误差、在全局坐标系下期望轨迹和实际轨迹对比和机器人实际速度、期望速度与对比方法的速度比较图，$d^{\ast }$估计



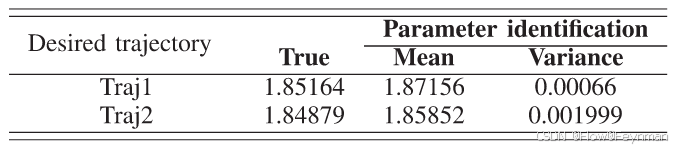
实验B：深度辨识。在本实验中，进一步验证了深度估计值$\hat{d}$可以同时收敛到$d^{\ast }$的真实值。为验证深度识别的有效性，取真值为1.876m。设置16组不同初始位姿和不同期望轨迹的跟踪实验，记录$\hat{d}$的稳态值，如下图所示。

1.7 复现的实验结果

本次复现这篇论文的速度控制器，将其用于期望轨迹（期望线速度为$tanh(t)$，期望角速度为$1.2\ast sin(t)$），控制器的参数为：$k_1=2.2,k_2=\pi /4,k_3=\pi /4,\Gamma =3$。复现的实验结果如下，

1.8 总结

这篇论文提出了一种具有速度饱和约束的视觉伺服跟踪控制器，能够实时估计未知深度。其实验结果表现得非常好，该控制器能够很好地将速度指令控制在速度饱和区域，而且需要调整的参数只有4个，对于实际应用非常友好。此外，基于Lyapunov技术和输入信号有界性分析了该系统的稳定性，证明了该系统全局渐进稳定。但是这个控制器在跟踪圆形轨迹的时候，前期(0~15s左右)跟踪效果不好，如下图所示。可以在该控制器中引入有限时间控制，使得该机器人在很短的时间收敛。
注意：本次复现的内容是通过python仿真实现的，所设计的期望轨迹并非是真实的图像序列，而是一个给定的期望机器人运动模型，通过该模型除以$d^{\ast }$来模拟期望机器人缩放的位姿信息。

其复现代码网站：论文复现，有需要的朋友可以参考。
参考文献：R. Wang, Z. Zhu, X. Zhang, Y. Fang and B. Li, “Visual Servoing Trajectory Tracking and Depth Identification for Mobile Robots With Velocity Saturation Constraints,” in IEEE Transactions on Industrial Electronics, vol. 71, no. 6, pp. 5950-5959, June 2024, doi: 10.1109/TIE.2023.3290254.