保姆级双目测距原理及代码

原创已于 2025-05-16 09:51:28 修改

· 3.6k 阅读

77 ·

版权

文章标签：

#深度学习 #机器学习 #人工智能 #双目测距

于 2025-03-16 12:14:01 首次发布

相机专栏收录该内容

4 篇文章

订阅专栏

一、双目测距基本流程

双目测距的大致流程就是：

双目标定 --> 立体校正（含消除畸变） --> 立体匹配 --> 视差计算 --> 深度计算(3D坐标)计算

下面将分别阐述每一个步骤并使用opencv-python来实现。

二、双目标定原理

2.1 相机标定目的

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。

摄像机标定的目的：求出相机的内、外参数，以及畸变参数。

相机内参包括：fx、fy、cx、cy

相机外参包括：R、T

畸变参数包括：径向畸变（k1, k2, k3）和切向畸变（p1, p2）

摄像机标定过程，简单的可以描述为：通过标定板可以得到n个对应的世界坐标三维点Xi（归一化后的平面）和对应的图像坐标二维点xi（畸变后的），这些三维点到二维点的转换都可以通过上面提到的相机内参K ，相机外参 R 和t，以及畸变参数 D ，经过一系列的矩阵变换得到。

2.2 理想相机成像原理（无畸变）

参考下面博客，里面详细记录了单目和双目相机的标定原理。

相机标定原理-CSDN博客摄像机标定过程，简单的可以描述为：通过标定板可以得到n个对应的世界坐标三维点Xi（归一化后的平面）和对应的图像坐标二维点xi（畸变后的），这些三维点到二维点的转换都可以通过上面提到的相机内参K ，相机外参 R 和t，以及畸变参数 D ，经过一系列的矩阵变换得到。https://blog.csdn.net/weixin_50174671/article/details/146291149?fromshare=blogdetail&sharetype=blogdetail&sharerId=146291149&sharerefer=PC&sharesource=weixin_50174671&sharefrom=from_link

2.3 Matlab双目相机标定过程

1、准备标定板、拍摄标定图像

首先，需要准备一个标定板，通常使用一个棋盘图案。标定板上有已知尺寸的正方形，用于估计相机的内外参数。使用双目相机分别从不同角度拍摄标定板的多张图片，确保标定板在每张图像中都有不同的视角。通常需要至少10张图片，且每张图像中的棋盘格应有不同的角度和位置。如下所示，分别为左图和右图：

2、利用matlab，对相机进行标定。

1、打开Matlab，点击APP，选择图像处理和计算机视觉模块中的Stereo Camera Calibrator，如下图所示：

2、然后点击Add Images，导入左右相机的图片，并且填入棋盘格的尺寸，标准的棋盘格尺寸一般都为25mm，点击确定，Matlab会自动检测每对图片的内角点，如下所示：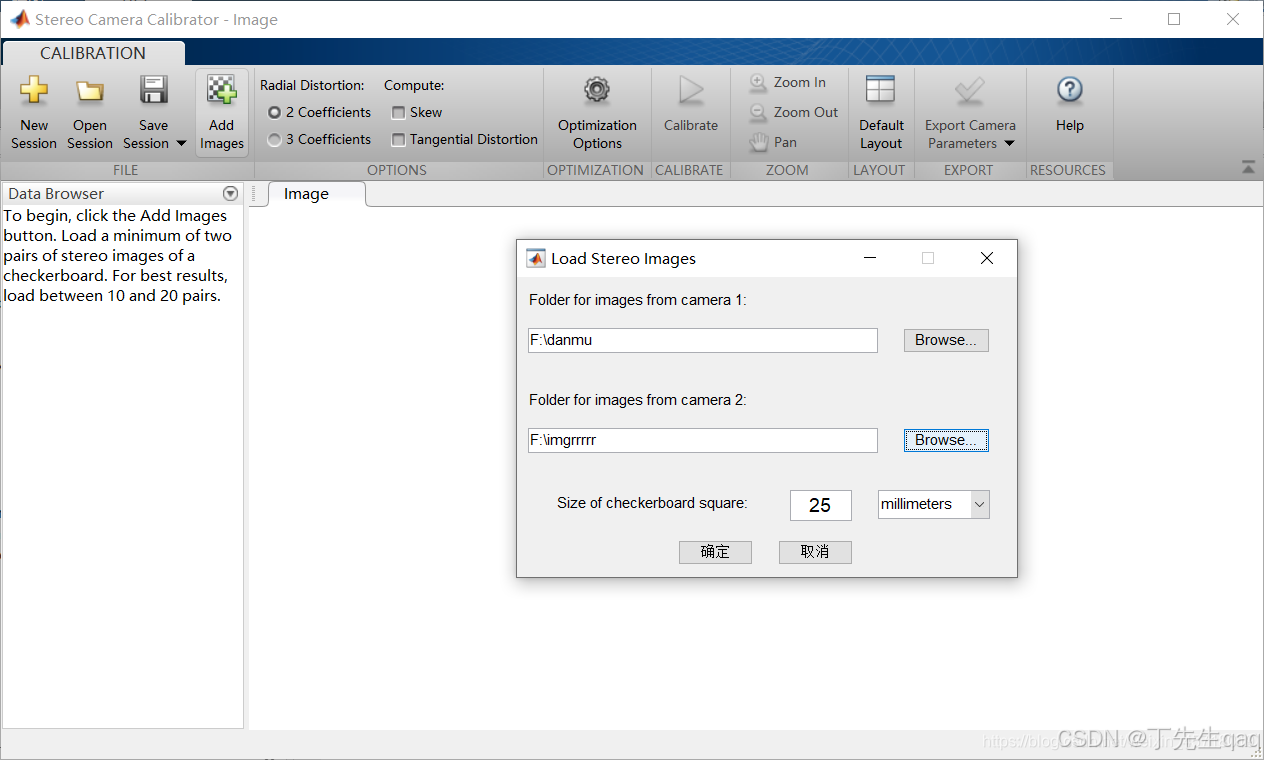

3、设置Radial Distortion，点击“Calibrate”开始标定：

Radial Distortion 为径向畸变。其中：

2 Coefficients选项的官方含义：使用四次多项式来估计透镜的径向畸变。
3 Coefficients选项的官方含义：使用六次多项式来估计透镜的径向畸变。此设置仅适用于大视场相机。

对于一般的相机选择2 Coefficients选项即可，对于大视场相机则选择3 Coefficients选项。

之后点击“Calibrate”开始标定，结果如下：

上图红色部分为标定误差，标定误差平均值小于0.3个像素，相机参数可用。（从标定误差中可以看出每张图片的误差，如果某张照片误差过大，可以在左侧图片列表中将其删除，会重新自动标注）。

3、标定完成，导出标定参数

标定完成后，点击Export Camera Paraeters，导出标定参数。如下图所示

然后双击下图红色框按钮，即可查看标定参数，参数的含义如下所示。

通过matlab标定后得到的旋转矩阵R和内参矩阵K，都需要转置以后才可以给OpenCV用，另外OpenCV畸变向量中前5个畸变系数的依次是：[k1, k2, p1, p2, k3]，由于切向畸变只标定了两个参数，则k3为0。

import numpy as np


# 双目相机参数
class stereoCamera(object):
    def __init__(self):

        # 相机分辨率
        self.width = 1920
        self.height = 1080

        # 左相机内参
        self.cameraMatrixL = np.array([[1.055680437718314e+03, 0, 9.413606455884707e+02],
                                         [0., 1.058770401061268e+03, 4.912941998043386e+02],
                                         [0., 0., 1.]])
        # 右相机内参
        self.cameraMatrixR = np.array([[1.054711146877877e+03, 0, 9.367704204123646e+02],
                                          [0., 1.058271948743051e+03, 4.916004426668275e+02],
                                          [0., 0., 1.]])

        # 左右相机畸变系数:[k1, k2, p1, p2, k3]
        self.distCoeffL = np.array(
            [[0.073021254486389, -0.062290081276031, 0.0, 0.0, 0.0]])
        self.distCoeffR = np.array(
            [[0.083500958126610, -0.165759745312155, 0.0, 0.0, 0.0]])

        # 旋转矩阵
        self.R = np.array([[0.999998470176857, -0.001725193865621, -2.887041248668339e-04],
                           [0.001724162019113, 0.999992258634731, -0.003536938781050],
                           [2.948037949908640e-04, 0.003536435597472, 0.999993703337170]])

        # 平移矩阵
        self.T = np.array([[-60.586970],	[-0.054678725657402],	[-0.140426987344030]])

三、立体校正（含消除畸变）

在介绍立体校正的具体方法之前，让我们来看一下，为什么要进行立体校正？

双目摄像机系统主要的任务就是测距，而视差求距离公式是在双目系统处于理想情况下推导的，但是在现实的双目立体视觉系统中，是不存在完全的共面行对准的两个摄像机图像平面的。所以我们要进行立体校正。立体校正的目的就是，把实际中非共面行对准的两幅图像，校正成共面行对准。（共面行对准：两摄像机图像平面在同一平面上，且同一点投影到两个摄像机图像平面时，应该在两个像素坐标系的同一行）,将实际的双目系统校正为理想的双目系统。

畸变矫正与立体校正流程如下所示：

读取相机标定参数（内参、畸变系数等）
使用 cv2.stereoRectify() 计算立体校正变换矩阵
使用 cv2.undistort() 对图像进行矫正
使用 cv2.initUndistortRectifyMap() 计算矫正映射
使用 cv2.remap() 进行映射变换

# 获取相机标定参数
camera_config = stereoconfig.stereoCamera()

# 极线校正
self.Rl, self.Rr, self.Pl, self.Pr, self.Q, self.validROIL, self.validROIR = cv2.stereoRectify(camera.cameraMatrixL, camera.distCoeffL, camera.cameraMatrixR, camera.distCoeffR,self.image_size, camera.R, camera.T, alpha=-1)

# 初始化畸变校正和映射表
self.mapLx, self.mapLy =cv2.initUndistortRectifyMap(camera.cameraMatrixL,camera.distCoeffL, self.Rl, self.Pl,self.image_size, cv2.CV_32FC1)

self.mapRx, self.mapRy = cv2.initUndistortRectifyMap(camera.cameraMatrixR,camera.distCoeffR, self.Rr, self.Pr,self.image_size, cv2.CV_32FC1)
 
 # 映射变换
 rectifiedL = cv2.remap(imgL, self.mapLx, self.mapLy, cv2.INTER_AREA)
 rectifiedR = cv2.remap(imgR, self.mapRx, self.mapRy, cv2.INTER_AREA)

经过这样的校正过程之后，两幅图中的极线就会完全水平，从而导致空间中的同一个点在左右两幅图中的像素位置位于同一行。这样寻找同名点对就可以只寻找同一行的像素，大大加快立体匹配速度。如下图所示，为校正完以在校正后的图片上画上一些等间距的平行线(也就是对极线)，利用这些平行线可以辅助我们来查看一下立体校正的结果是否准确。

四、立体匹配与深度图计算

4.1 立体匹配和视差图计算

立体匹配的目的是为左图中的每一个像素点在右图中找到其对应点（世界中相同的物理点），这样就可以计算出视差：（和分别是两个对应点在图像中的列坐标）。大部分立体匹配算法的计算过程可以分成以下几个阶段：匹配代价计算、代价聚合、视差优化、视差细化。

立体匹配是立体视觉中一个很难的部分，主要困难在于：1.图像中可能存在重复纹理和弱纹理，这些区域很难匹配正确；2.由于左右相机的拍摄位置不同，图像中几乎必然存在遮挡区域，在遮挡区域，左图中有一些像素点在右图中并没有对应的点，反之亦然；3.左右相机所接收的光照情况不同；4.过度曝光区域难以匹配；5.倾斜表面、弯曲表面、非朗伯体表面；6.较高的图像噪声等。

比较好用的是SGBM算法，它的核心是基于SGM算法，但和SGM算法又有一些不同，比如匹配代价部分用的是BT代价（原图+梯度图）而不是HMI代价等等。（SGM算法自行百度）

在立体匹配生成视差图之后，还可以对视差图进行滤波后处理，例如WLS、Guided Filter、Fast Global Smooth Filter、Bilatera Filter、TDSR等。视差图滤波能够将稀疏视差转变为稠密视差，并在一定程度上降低视差图噪声，改善视差图的视觉效果，但是比较依赖初始视差图的质量。

# SGBM算法初始化
self.sgbm = cv2.StereoSGBM_create(minDisparity=0, numDisparities=16 * 5, blockSize=3, P1=8 * 3 * 3, P2=32 * 3 * 3,disp12MaxDiff=12, uniquenessRatio=10, speckleWindowSize=50, speckleRange=32, preFilterCap=63)

# WLS滤波器配置
if use_wls:
  self.wls_filter = cv2.ximgproc.createDisparityWLSFilter(self.sgbm)
  self.wls_filter.setLambda(80000)
  self.wls_filter.setSigmaColor(1.3)
  self.right_matcher = cv2.ximgproc.createRightMatcher(self.sgbm)

4.2 深度图计算

到了视差图之后，就可以计算像素深度了，公式如下（推导略）：

其中 f 为焦距长度（像素焦距），b为基线长度，d为视差，（ $c_{xr}-c_{xl}$ ）为两个相机主点的列坐标的差，默认为0即可。

在opencv中使用StereoRectify()函数可以得到一个重投影矩阵Q，使用Q矩阵也可以将像素坐标转换为三维坐标。函数将视差图，通过投影矩阵Q，得到一副映射图，图像大小与视差图相同，且每个像素具有三个通道，分别存储了该像素位置在相机坐标系下的三维点坐标在x, y, z,三个轴上的值，即每个像素的在相机坐标系下的三维坐标。

points_3d = cv2.reprojectImageTo3D(dispL, self.Q)
# 可视化深度图
depth = points_3d[:, :, 2]
depth_colormap = self.get_visual_depth(depth)

不使用WSL滤波生成的深度图

使用WSL滤波生成的深度图

通过上面两幅图对比可见，使用WLS后，深度图的噪声明显减少，边缘部分更加平滑，细节保留得更好。相比未使用WLS的深度图，WLS可以有效抑制纹理区域的误匹配，同时增强边缘对比度，使得深度估算更加精准。此外，在低纹理区域（如墙面、天空等），WLS能够减少伪影，使视差过渡更加自然，提高双目测距精度。

五、整体代码介绍

双目立体视觉测距，包括畸变矫正、立体校正、视差计算和三维重建。首先，代码从 stereoconfig 读取相机标定参数，包括内外参、畸变系数等，并使用 cv2.stereoRectify() 进行立体校正，确保左右相机的图像对齐。接着，利用 SGBM（Semi-Global Block Matching） 计算视差图，并通过 WLS（加权最小二乘滤波） 进行优化，使视差图更加平滑，减少噪声。然后，使用 cv2.reprojectImageTo3D() 将视差图转换为 3D 坐标，获取每个像素点的真实三维位置。

程序提供两种模式：图片模式（image_mode）用于处理静态图像，相机模式（camera_mode）用于实时获取双目相机的视频流，并进行测距。用户可以点击深度图像查看对应点的 3D 坐标，最终可视化校正后的图像、视差图及深度图，为立体视觉应用（如机器人、AR/VR 及自动驾驶）提供了基础。代码仅仅依赖 numpy和opencv库，安装命令如下：


pip install numpy opencv-python -i https://pypi.tuna.tsinghua.edu.cn/simple

代码效果如下：

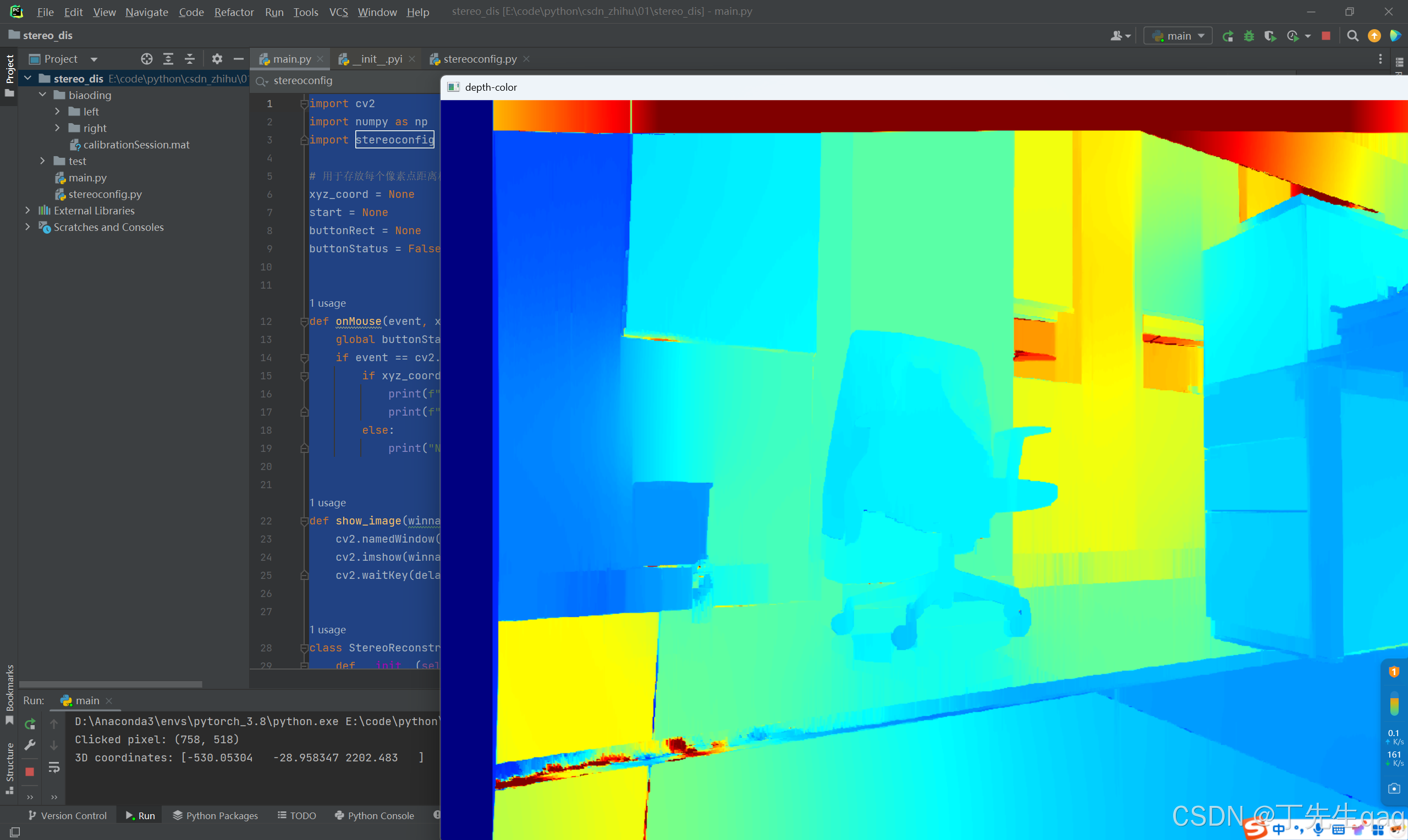
关于该系统涉及到的完整源码、UI界面代码、数据集、训练代码、测试图片视频等相关文件，均已打包上传，感兴趣的小伙伴可以通过下载链接自行获取。

【获取方式】：双目测距代码