探秘双重机器学习：因果推断新视角，揭开模型参数偏误之谜！

最新推荐文章于 2025-04-08 17:56:09 发布

不一样的邓先生

最新推荐文章于 2025-04-08 17:56:09 发布

阅读量6.1k

点赞数 20

分类专栏： python 文章标签：机器学习人工智能

本文链接：https://blog.csdn.net/weixin_50249953/article/details/137613423

版权

python 专栏收录该内容

10 篇文章

订阅专栏

本文介绍了双重机器学习在因果推断中的作用，强调了其在解决传统模型维度问题和提高参数估计准确性方面的优势，通过半参数模型示例展示了偏差的来源及内曼正交和交叉拟合的应用。同时，提到了在Stata中使用ddml命令的实践步骤和一篇实证应用论文的推荐。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

今天给大家分享的内容是双重机器学习知识，双重机器学习是因果推断领域发展起来的较新的研究内容，实现了机器学习和因果推断领域的结合，我们知道机器学习更加注重模型的预测，这在一定程度上会导致参数估计的偏误，双重机器学习在一定程度上纠正了这种偏误，从而实现了机器学习在因果推断领域的研究，对于双重机器学习的知识，我们主要借助于以下两篇论文：Double/debiased machine learning for treatment and structural parameters和 ddml: Double/debiased machine learning in Stata，其中第一篇文章是双重机器学习的理论介绍文章，该文章理论知识深厚，数学表达式丰富；第二篇文章是双重机器学习结合了stacking思想在stata中的实现，包含重要的理论知识和代码演示。

因果推断的开始和发展是从传统的计量模型中起步，既然传统的计量模型也可以进行因果推断，那么我们为什么还要发展出机器学习的方法来辅助因果推断呢？学术的发展都是讲究一定的效用和意义的，如果仅仅是换了种方法来实现同样的效果，那么该方法的认可度并不会太高，双重机器学习能够在学术界得到一定程度的认可，那么说明该方法相对于传统方法来说，是具备一定的突破性。

因此我们首先讲一讲双重机器学习在传统模型上面的突破，研究表明传统非参数模型会陷入维度诅咒，也就是说传统非参数模型在高纬数据上得到一个较差的估计量，而机器学习相关的算法是基于数据驱动，因此在高纬和非线性数据关系捕捉性能表现较好，因此使用机器学习的方法可以克服传统模型在维度上的诅咒，在这里我们提一下，计量经济学中的高维和机器学习中的高维的差别，首先，高纬是拥有大量的特征和变量，这个大量是多大我们不知道，但是在计量领域认为数据的维度大于数据的个数就称为高维数据，在机器学习的角度，是对数据量会有一定的要求，因此，仅仅从数据的特征数量来说是很少超过数据量的，高纬的情形不是很普遍，同时我们将特征与特征之间的关系或者高次方项，我们统一考虑为交互关系或者非线形关系，机器学习关注预测，因此在实际的建模过程中我们并不会特意构造类似的特征数据做为新的特征，但是传统的计量模型中注重模型的解释，因此，特征与特征的交互，特征的高次方、对数关系就显得尤为重要，我们在实际回归模型构建过程中经常会人工手动构建出一些非线形的特征来考虑对变量的影响，因此在论文中会出现特征随着数据量的增大而不断扩张，从而出现在传统模型中存在的维度诅咒，随着数据的不断增大，数据之间的关系也变得复杂，尽管原始的特征没有变化，但是由于数据之间的复杂关系，因此在传统模型中就必须考虑到特征之间的非线形关系等，例如：交互项、高次方等，然而机器学习在处理这些问题具有一定的优势。

OK，我们已经解决了我们提出的第一个问题，使用机器学习来进行建模不就可以了吗？如果是这么简单就好了，第二个问题出现了，既然这么好，那么为什么机器学习出现之后，传统经济模型在因果推断领域生生不息，大家可以去了解该方面的文章，因果推断还是传统模型居多，说明什么？机器学习在因果推断领域会有一定问题，当然这一方面我还没有过多的探究，其中一个方面的话，我个人认为是“黑盒理论”，机器学习缺乏可解释性，尤其是在经济领域，在一个复杂的问题研究，可能也需要较为复杂的模型来模拟现实情况才可能得到较为准确的结论，因此，集成模型等复杂模型等使用可能更为普遍，但是确定也十分明显，模型的解释性缺乏，只知道结果，不知道如何产生。第二个方面的话，就想文章中说到的机器学习来研究经济问题是存在偏误的，因果推断注重解释，因此在有限数据的情况下，模型的偏误越小越好，但是机器学习追求泛化能力，因此会要求牺牲训练数据的准确性，来实现泛化能力，如果将机器学习直接使用到参数估计，会参数较大的偏差，并且随着数据量的增大，这个偏差会不断增大的，后续会有公式推导。因此，作者提出了双重机器学习的方法来降低这个偏差，最终得到参数的一致估计。

我们先以半参数模型为例来讲述直接使用机器学习的方法会产生偏差的原理，经典的半参数模型如下：

其中D是我们的政策或者实验效应变量， $\theta_{0}$ 代表D的参数，也就是我们要估计的变量， $g(x)$ 代表我们要考虑的一系列控制变量，用非参数的形式表示，U是残差。我们可以构建一个机器学习模型 $D\hat{\theta_{0}}+\hat{g_{0}(x)}$ 与目标变量Y进行回归可以得到我们的估计量 $\theta$ ，得到下面公式：

我们将 $Y_{i}$ 带入，同时乘以 $\sqrt{n}$ ，可以得到下面结果：

显然右边第一部分公式服从正态分布，均值为0，右边第二部分公式为我们估计的量与真实值之间的差距，即偏差 $g_{0}(x)-\hat{g_{0}(x)}$ ，收敛速度为 $n^{-\varphi g}\sqrt{n} \rightarrow \propto$ ,大家应该可以理解，D是一个常数，因此收敛速度取决于 $g_{0}(x)-\hat{g_{0}(x)}$ ,我们假设收敛速度为 $n^{-\varphi g}$ ， $\varphi g<1/2$ ,因此整个表达式是趋近 $\propto$ ，换句话说，随着样本量的不断增大，我们估计的参数 $\hat{\theta_{0}}$ 由于偏差的存在，会越来越偏离我们的真实值。因此作者引入了内曼正交和交叉拟合较好的解决了这个问题，从而使得我们能够得到一致的估计量，引入内曼正交之后，模型变成了

我们求解得到估计量如下：

和上面一样，通过带入即可得到如下分解：

我们可以得到分解出来得到的a仍然是正态分布，均值为0，对于b就是我们得到的偏差项，主要有两部分组成，分别是 $V_{i}=\hat{m_{0}(x)}-m_{0}(x)$ 和 $g_{0}(x)-\hat{g_{0}(x)}$ ，在使用样本分割的情况下，使用辅助样本的情况下， $E(V|X)=0$ ,同时根据切比雪夫不等式，得到

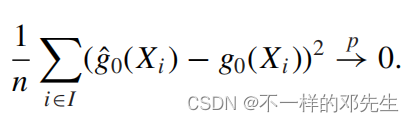
因此根据上面的条件我们分解得到的b项会以概率趋近于0，因此在对样本的进行分割的前提下，使用辅助样本来进行机器学习估计，使用主样本来进行参数估计，我们将会使得残差逐渐减小最终消失，从而得到一致的估计量，这里特别强调了一些要使用样本分割来进行参数估计和机器学习估计，因为如果说使用全样本来进行机器学习和参数估计的话，将不会得到一致的估计并且会产生较大的偏差，在上面公式中的呈现就是U和V存在相关，可能不一定满足均值为0的正态分布，但是如果不使用全样本进行估计，会导致一定效率损失，因此，作者提出的方法是使用交叉拟合的方法，对样本进行多折划分，使用其中的一部分得到机器学习估计量，剩余的样本得到参数估计，对不同选择下的参数估计求均值或者中文数得到最终的估计量。

对于上面辅助模型的构建，作者采用的是内曼正交的思想，具体关于内曼正交相关的知识作者在论文中有所呈现，大家感兴趣可以自行下载阅读，核心的作用就是，第一阶段的估计量的偏差不会对第二阶段估计量产生较大影响，我们对于参数 $\theta$ 的估计可以通过分数函数求期望得到，在传统模型下得到的分数函数为 $\varphi (x;\theta ;\beta )=(Y-D\theta -g(x))D$ ,对分数函数的期望求倒数得：

大家可以看到分数函数的一阶倒数不等于0，说明什么 $\theta$ 的估计对第一阶段的机器学习的估计量很明感， $g_{0}(x)$ 的微小变化也会引起 $\theta$ 估计的变化。我们引入内曼正交之后，分数函数变成了： $\varphi (x;\theta ;\eta )=(Y-D\theta -g(x))(D-m(x))$ , $\eta =(m,g)$ 分数函数期望的一阶导数变成了

也就是说机器学习g估计量误差的微小变化不会影响到最终参数的估计，参数的估计量保持稳定，第一阶段机器学习的估计偏差不会影响到第二阶段OLS参数估计，从而导致第二阶段参数的一致性。以上就是Double/debiased machine learning for treatment and structural parameters这篇论文相关的核心思想和理论，本来是想给大家结合第二篇文章进行一个讲解，突然发现也没有什么好讲的了，第二篇文章侧重于双重机器学习思想的实际应用，说明了算法的实际应用流程，并在stata中提供了命令，大家可以查看，我们就说一些比较重要的吧，stata中使用ddml命令需要借助python环境，因为很多机器学习模型都是使用python中scikit-learn中的模型，因此需要安装python和scikit-learn包，大家可以自行安装，这一块可以参考网上资料，安装完成之后在stata中引入python环境即可使用，步骤如下：

输入python search 获取python安装目录，使用python set exec 路径引入python环境，我接着按照论文中给出的部分线形模型使用stacking来进行操作，如果说大家中途有什么其他的问题基本就是包文件没有安装或者版本不适配等。

结果如下：

最后你给大家推荐一篇关于双重机器学习实证应用等论文，网络基础设施、包容性绿色增长与地区差距———基于双重机器学习的因果推断这一篇论文是发表在数量经济技术经济研究上面2023年的文章，还算是比较新的，大家可以借鉴学习，如果说不想去知网下载，可以关注我的公众号“明天科技屋”，回复数字关键词“0005”即可获得，上面的两篇文章也会一起发送！希望大家多多关注，并给公众号文章点点赞👍！