机器学习——词向量模型（纯理解）

挖坑…要么我来填坑，要么把我填坑
反正…闲着也是闲着，那就薅自己头发，虐自己脑袋
适度自虐，有助于身心健康，阿弥陀佛…

走了很多弯路，看了很多乱七八糟的word2vec，连潜在语义分析也看了，数学计算是整明白了，但为什么要这么算，这么算是什么个意思，我却迷迷糊糊
脑海里，并没有形成一个完整的思路，也没有一个系统的框架
但目前并没有打算完完全全地梳理，虽然说先有个宏观框架，更利于理解，但有时候我却感觉到，如果一个事物过于庞大且神秘时，宏观层面也只是浮光掠影，倒不如凿开硕大城堡的一个小墙角，钻进去才能窥见内里。
仔仔细细地看了下边这篇，写的很详实，很仔细，很好
前大半部分是可以看懂数学计算，但看不懂计算的意义
word2vec 中的数学原理详解
后半部分：啥都没看懂
估计还要重头再看几遍，或是找些其他的资料。。。唉。。。好难

下边这篇，让我大致理解了训练过程数据的变化，嗷。。。太牛了
举例说明CBOW训练时的数据变化

直到我看到这篇NLP笔记之word2vec算法（2）–Hierarchical Softmax原理+数学推导 - 张小彬的文章 - 知乎
我天呐。。。瞬间有种顿悟的通透感！
虽然还是有一些不明确的地方，但是朦胧之中，抓住了一丝丝的脉络

感觉可以键步如飞，自己梳理一下了
em。。。要从什么地方开始梳理呢

word2vec基础认识

看别人总结的关系，很清晰了。

在看各种文章的分析时，讲了很多的内容，由于内容过于庞大，导致我出现了很多混淆的地方，这里主要只讲解CBOW模型。

为了更方便自己理解，且减少工作量，只梳理【基于HierarchicalSoftmax模型下的CBOW模型】

先理解【基于HierarchicalSoftmax模型下的CBOW模型】，想必会让我脑子里炸掉的神经线，更清晰一些。

首先，CBOW是应用语料来训练出一个CBOW模型，
再根据上下文的词（如下方的cats likes和run and是上下文），应用训练好的CBOW模型，来预测出中间词的模型。

但实际上，CBOW模型在预测时，并不会考量上下文的词序，也就是说，词语的顺序并不影响最终的模型预测结果。
cat likes run and，run cat like and，and cat run likes这些乱序词预测出的，都是一样的结果
具体CBOW为什么无法考虑词序，这个后续再分析。
个人目前看法，待日后打脸再来改

在训练语料前，需要对语料进行分词处理（把句子拆分成单词），这样可以得到【一个不含重复词的词典D】以及【含有重复词且含语序的语料词库C】

例如，语料为这三个句子：
I like to eat pizza.
The sun is shining brightly.
The cat is sleeping peacefully on the cozy mat
整理成词典D：I, like, to, eat, pizza, The, sun, is, shining, brightly,
整理成语料库C：具体语料库C到底是什么样的，我还不确定，暂定如此，日后再改
[“I”, “like”, “to”, “eat”, “pizza.”]
[“The”, “sun”, “is”, “shining”, “brightly.”]
[“She”, “is”, “reading”, “a”, “book.”]

其中，假设统计出词典D里总共有N个词，从语料词库C中可以统计出这N个词的词频（就是每个单词在预料中出现的次数）

最终根据语料，完成训练，并根据上下文，对关键词进行预测

word2vec流程

这里参考了如何通俗地理解word2vec
模型训练有两个方向：正向传播、反向传播

• 正向传播：是从输入层开始，按照当前模型参数进行计算，最终在输出层得到计算结果
• 反向传播：是根据输出层的计算结果，来反向迭代模型的参数，使整个模型变得更好。

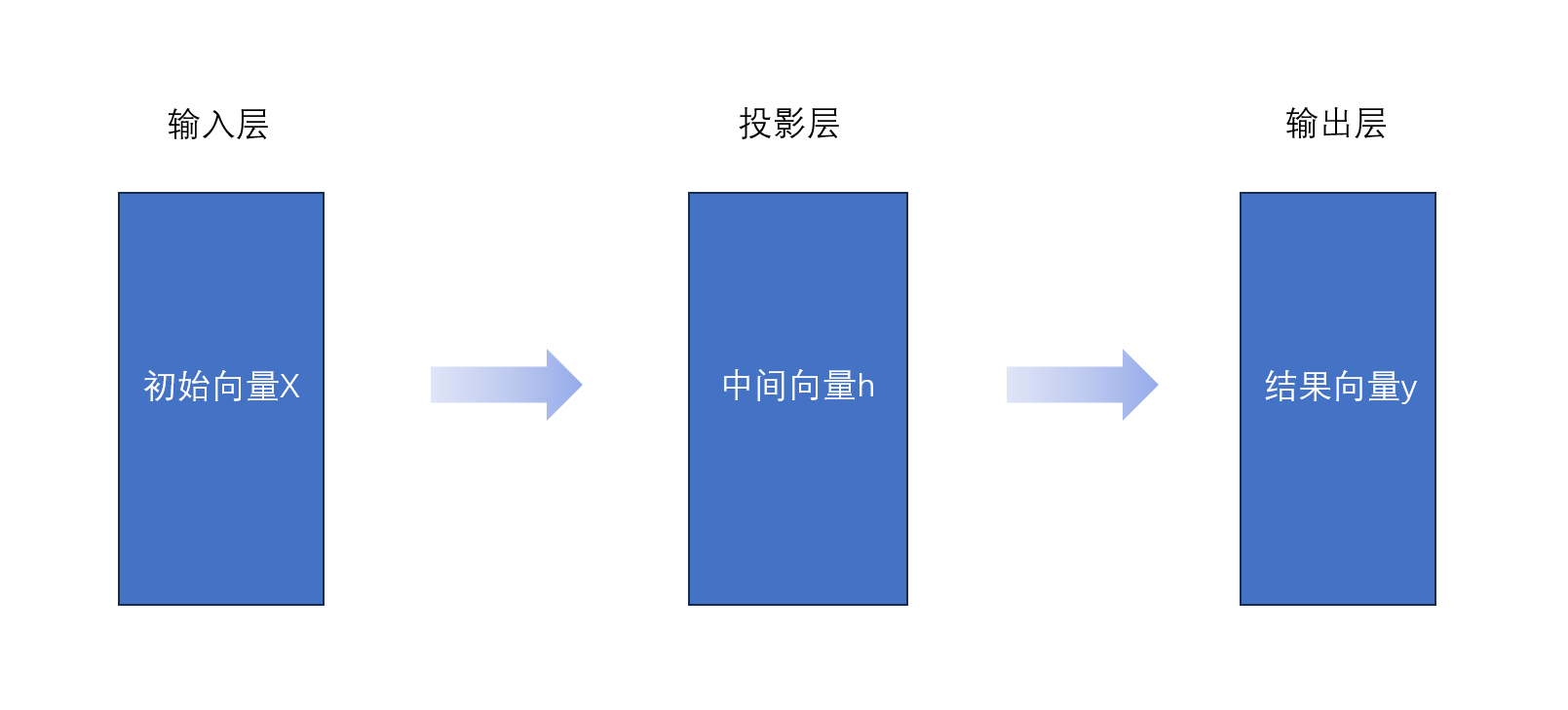
CBOW模型的三层：输入层、投影层（隐藏层）、输出层

【基于矩阵下的CBOW模型】和【基于HierarchicalSoftmax模型下的CBOW模型】，在输入层和投影层的操作，基本是一样的

这两者的区别在于输出层的处理上，以及反向传播时的迭代方式上

实际上输出层的处理，还有第三种方式：负采样，但考虑到一下子梳理太多东西，头发可能会默默变成地中海，还是算了，先梳理基础的两种

正向传播通用流程

首先是正向传播的两个环节：

正向传播过程

• 输入层：
  • 将词典D转换为one-hot独热编码，
  • 按规定上下文的长度k，来截取语库C里的上下文单词$x$和预测单词$y\ast$
  • 获取上下文单词x的独热编码向量$x1$,$x2$,$x3$,$x4$，作为初始输入矩阵X=[$x1$,$x2$,$x3$,$x4$]
• 投影层：
  • 将初始矩阵X乘以一个权重矩阵W，提取出各个初始向量$x1$,$x2$,$x3$,$x4$的权重系数$w1$、$w2$、$w3$、$w4$
  • 将这些权重系数加和，作为中间向量h=[$w1$+$w2$+$w3$+$w4$]，注意，这里的加和是按列加和
• 输出层：
  • 设计迭代模型，计算迭代式（这里的迭代模型，将是重难点）

正向传播的目的，就是根据当前的模型参数，按照各环节的模型函数进行计算

重点就在于正向传播过程中各环节所涉及的模型参数和模型函数，以及这些模型参数和函数的意义何在。

反向传播通用流程

• 迭代输出层的参数
• 迭代投影层的参数

模型参数和模型函数是什么，为什么，有什么用
接下来，根据输入层、投影层、输出层这三个环节来详细看看

CBOW模型流程1：输入层

输入层：

• 将词典D转换为one-hot独热编码，
• 按规定上下文的长度k，来截取语库C里的上下文单词$x$和预测单词$y\ast$
• 获取上下文单词x的独热编码向量$x1$,$x2$,$x3$,$x4$，作为初始输入矩阵X=[$x1$,$x2$,$x3$,$x4$]

转换独热编码

由于单词是无法进行数学计算的，因此，我们需要先将单词转换为独热编码，目的是用数学向量来单独表示某个单词。

首先是将词典D中的所有单词，都转换为独热编码。

词典D中总共有N个单词，那么每个单词的向量就总共有N个元素。
例如：词典D为
[“I”, “like”, “to”, “eat”, “pizza”, “The”, “sun”, “is”, “shining”, “brightly”, “cat”, “sleeping”, “peacefully”, “on”, “the”, “cozy”, “mat”]
共有17个单词，那么每个单词都是17个元素作为向量

I: [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
like: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
to: [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
eat: [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
pizza: [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
The: [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
sun: [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
is: [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
shining: [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
brightly: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
cat: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
sleeping: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]
peacefully: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
on: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
the: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]
cozy: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
mat: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
但需要将上述的行向量，全部转为列向量，因为数学中一般是以一列元素作为向量表示

获取上下文

获取上下文的2c个单词，一般称为背景词$x$
还要获取待预测的关键单词，$y\ast$

例如c=2时，就意味着要获取关键单词前、后各2个单词作为背景词，也就是背景词总共有4个
并将这4个背景词抽出对应的独热编码

待解决：其实也要考虑有时候，无法获取完整的背景词的情况，这需要用填充词代替，具体等之后再操作，先把主体的梳理干净

获取独热编码

记得将下列的向量转为列向量

例如the这个上文的单词向量$x1$如下，
$\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$
另外还有其他三个单词向量，均分别表示为$x2,x3,x4$

则输入向量就是X=[x1,x2,x3,x4]，X是$N\times 2c$的矩阵，N是向量的位数，2c是上下文获取的2c个单词
其中每一列表示的是每个单词的独热编码向量。

但要知道，我们是要对全部语料进行训练，因此就不可能只输入一个上下文来训练，而是输入所有的上下文，同时进行训练

所以，初始输入向量，应该是个三维的数据，

$X=[X1=[x1,x2,x3,x4]，X2=[x1,x2,x3,x4]，X3=[x1,x2,x3,x4].....]$

$X1$、$X2$、$X3$这些是每个上下文，总共有多个上下文（不需要数），里边的$[x1,x2,x3,x4]$表示的是每一个上下文对应的独热编码向量

CBOW模型流程2：投影层

投影层：

• 将初始输入的每一个上下文独热编码向量$X_i$乘以一个权重矩阵W，提取出各个初始向量$x1$,$x2$,$x3$,$x4$的权重系数$w1$、$w2$、$w3$、$w4$
• 将这些权重系数加和，作为中间向量h=[$w1$+$w2$+$w3$+$w4$]，注意，这里的加和是按列加和

将初始输入向量，转化为中间向量时，需要乘以一个权重系数矩阵W，但我一直很困惑，这个W的意义到底是什么？

百搜不得其解，so sad
于是我自己猜想，这个权重系数矩阵，保存的是每个单词隐藏的词性特征
比如一个单词的词性有：褒贬义、动名形容词等等词性，但是在数学中却不会明显地设计出来，而是通过多个特征数值来表示，但！由于训练过程，参数是自动迭代的，我们也不知道划分出来的特征到底是哪种词性。
就比如，我们要形容一个人，如果形容的维度越多，那么这个人也就更加具体：身高、体重、收入等等
同样的，如果我们给一个单词设定的特征数越多，那么描述这个单词的数据也就更丰富，对这个单词的词性可能也就更具体（依然不确定设定的特征到底是单词的哪个词性）

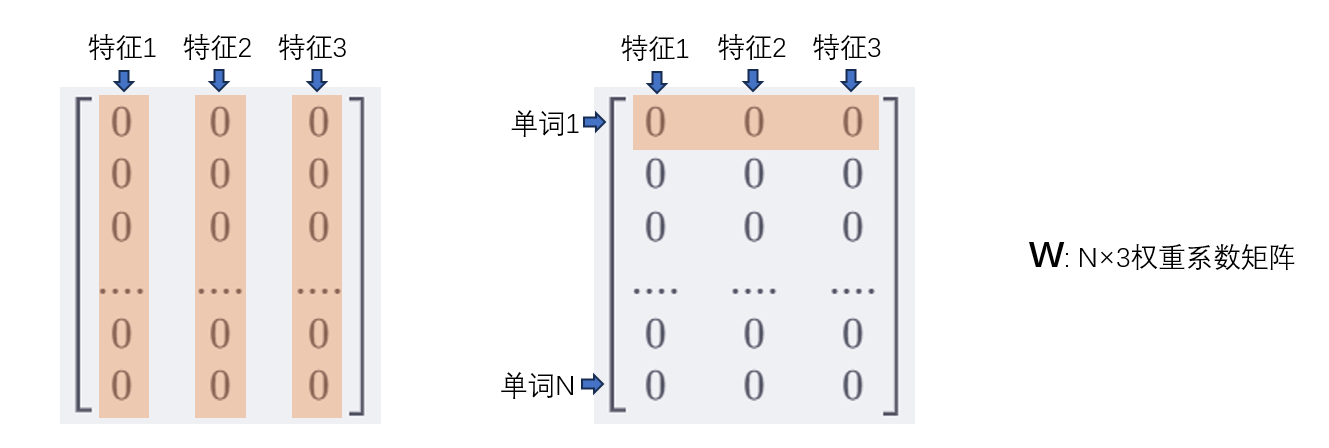
比如，给每个单词都设定3个特征，而词典D总共有N个单词，那么W就是一个N×3的矩阵
先将权重W矩阵初始化为0，后续在反向传播时再迭代更新
$\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$

这样，每个单词都有其各自对应的权重系数特征

现在要分别抽取出4个背景词对应权重系数特征，

而如果要让4个背景词，都获取到各自的权重系数特征，则只需用向量乘法 $W^T{X}_1$
即可得到一个3x4的矩阵，每一列对应的是各个上下文单词的权重系数特征

得到权重系数特征矩阵后，再将每个单词的权重系数特征，按相同特征加和（即按列加和），最终得到一个3×1的中间向量h

$h=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$+$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$+$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$+$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$=$\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$

所以，中间向量h实际上，是一个上下文背景词的各特征之和（不是所有特征都加一起，而是按特征来分别求和）。

但要注意，上边只是演示了一个上下文最终生成的中间向量，实际有很多个上下文，都会生成各自对应的向量

因此，就会有多个h

$H=[h_1,h_2,h_3....]$

另外，每个上下文都有唯一要预测的关键单词$y\ast$

所以，为了表示方便，我们可以将要预测的单词表示为$word$

$word$主要是为了后续计算表达方便，可以先暂时这么记

CBOW模型流程3：输出层

⭐【基于矩阵下的CBOW模型】流程

1. 构建矩阵U

首先，这个矩阵U到底有什么用？

矩阵U，其实算是上下文与关键词之间的关系参数

我们知道，在投影层中，每个上下文都会对应生成一个中间向量h

那么这个中间向量h其实就是一个上下文的数据表示

但这个上下文到底能够预测出哪个关键词呢？

这就需要上下文与关键词的关系参数来表示。

这个上下文的中间向量h，与每个关键词的关系参数的乘积，则可以设计为上下文与关键词的关系程度。

就好像h是一把钥匙，而词典D里的每一个关键词都是一把锁，h到底能开哪把锁呢？
我们可以自行设计规则，规则就是：h跟每个关键词的参数相乘，乘积最高的那个就是h预测出的关键词

• 那么在后续训练这个规则时，我们只要想办法多次迭代，让每个上下文的h向量和它对应的待预测关键词参数的乘积达到最高，这个规则不就形成了吗！

• 这个过程就像是社会教育，如果社会的目标是提高全民教育水平。
  为了达到这个目标，可以设置一个规则：高学历才能高薪
  那么要如何使规则成立呢？
  就是在日后招聘的时候，给高学历高薪，给低学历低薪，这样筛选机制下，让低学历的人回炉重造，这样就会让每个人都竞相追逐高学历
  于是整个社会就会在规则的奖惩下，逐渐提高了全民的教育水平
  这样的价值倡导是不对的！仅作举例

• 但要如何评价一个人是否是高学历呢？这也是我们设定的规定

  • 我们可以设置3个参考维度：毕业院校、学历水平、国内国外
  • 这一步相当于我们投影层计算出来的h
  • 如果这三个维度表现越强，则学历越高！薪资越高！越有助于我们达到目标

• 要衡量这三个维度的综合表现，我们需要让每个参考维度都有一个权重系数，这个权重系数，就相当于u向量

因此，我们让每个关键词，都有一个参数向量u，这个参数向量是和h向量相乘得到一个值，因此参数向量的系数个数是和中间向量h的值个数是一致的。

所有关键词的参数向量就会组成一个矩阵U

但通常我们是无法设计出具体的参数向量u的，所以采取初始化的方式，先初始化一个矩阵U

2. 计算关系值

我们说过，一个上下文的数据表示是h向量，这个上下文与每个关键词的乘积值，则表示它们的关系强弱

那应该用h去和每个关键词的u参数相乘，得到一个乘积值

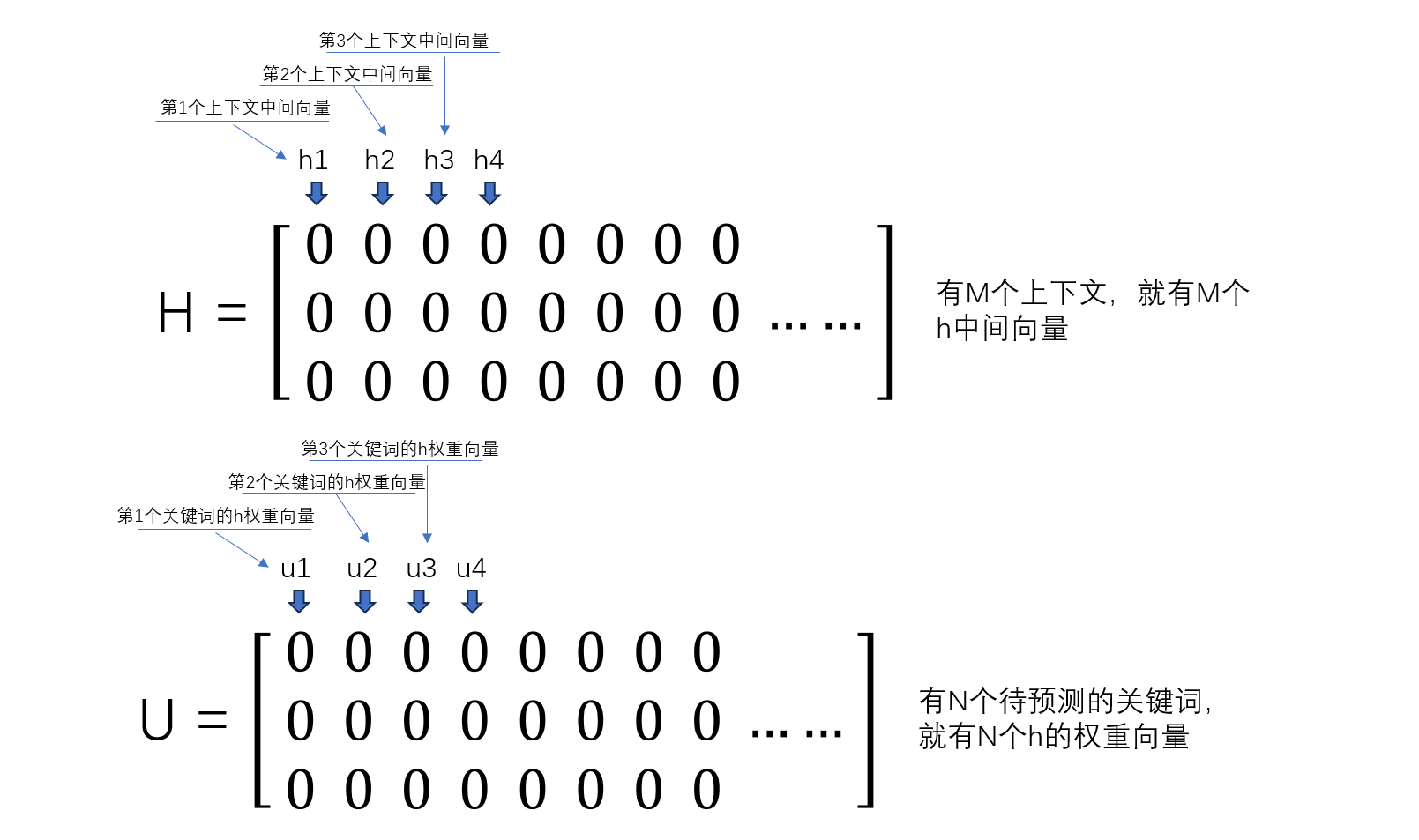
我们知道，投影层的中间向量h，表示的是上下文单词向量的三个特征数据分别之和，形状为3x1

而所有的上下文中间向量h，构成一个3xM的H矩阵

而要衡量上下文与每一个待预测的关键词之间的关系，需要一个参数矩阵$U$

参数矩阵$U$里的一个向量u中含有3个值，这三个值实际表示的是对中间向量h的特征1、特征2、特征3的权重系数，而u和h的点乘得到的单个值，实际上就是待预测的关键词与上下文的特征之和h的关系表示。

相当于，如果有一个上下文简称为context1的中间向量为h1，那么这个中间向量与哪个待预测的关键词关系最大呢？

这就需要我们让h1和所有关键词的向量u，逐一进行点乘

context1与第一个关键词的关系：值1 = h1u1
context1与第二个关键词的关系：值2 = h1u2
context1与第三个关键词的关系：值3 = h1u3
context1与第…个关键词的关系：
context1与第N个关键词的关系：值N = h1uN

这时得到的N个值，需要通过softmax函数来衡量，softmax(值)最大的，即为关系最大的待预测关键词。

那么，有M个上下文，每个上下文的中间向量h有3个特征值，因此，M个上下文构成的中间矩阵H为Mx3

而待遇测的关键词有N个，每个关键词都有3个值表示向量h的3个特征值的权重值，因此，U矩阵为Nx3

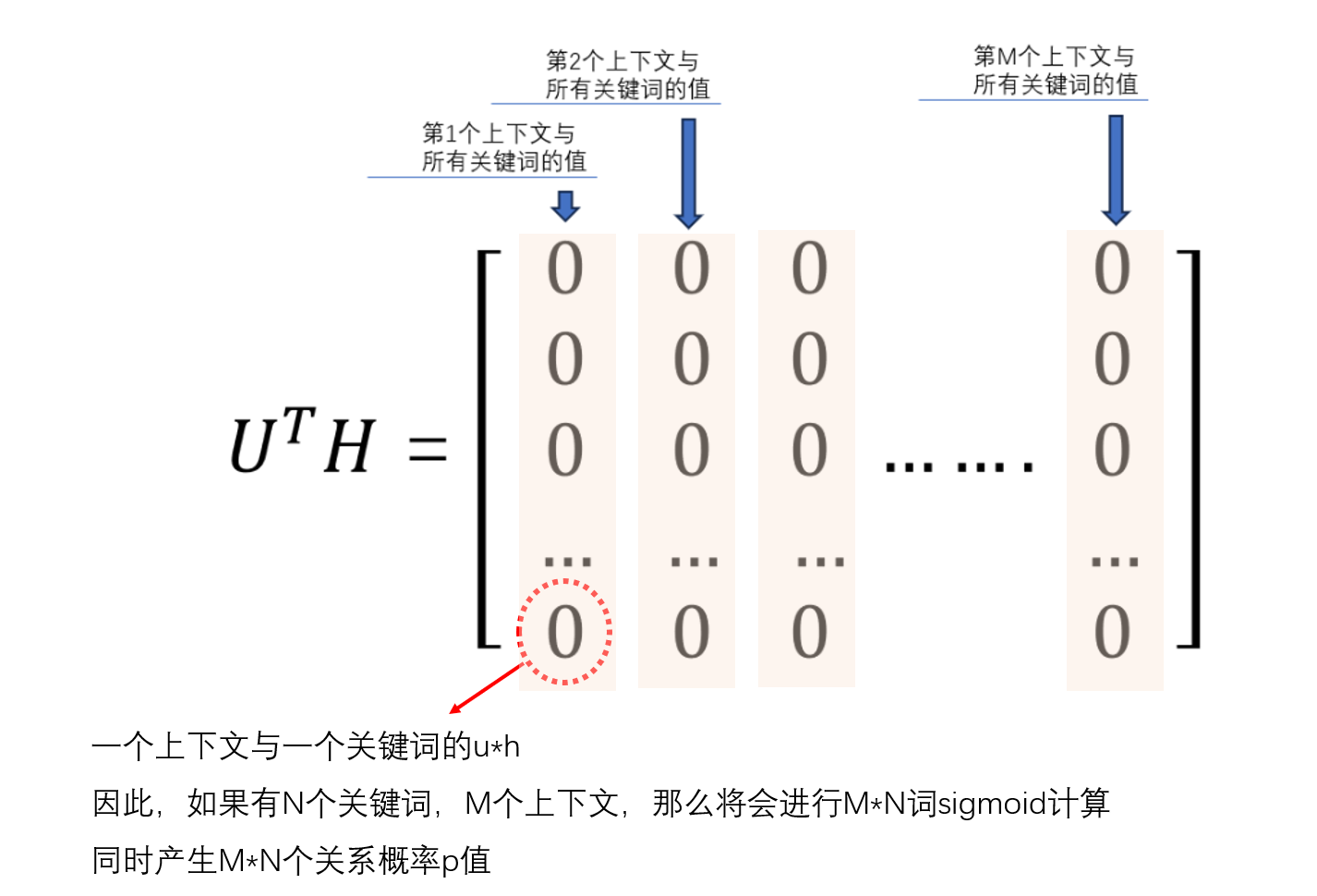
$U^{T}M$的结果是一个N×M的矩阵，N行M列，每一列表示每个上下文与N个上下文的值

3. 构建优化函数，计算sigmoid值

将每一个上下文，与所有的关键词的关系值，进行一个二分类的概率计算，即sigmoid计算

这个二分类的概率计算，是用于表示一个上下文与一个关键词是否为正确的待预测关键词的概率表示。

我们知道，一个上下文，对应唯一一个关键词，这个对应的关键词，我们姑且称为这个上下文的正确关键词

那么就有两种情况：一个上下文和一个关键词的对应关系

• 正确关键词（word=w*)：最好能尽可能提高上下文与正确关键词的关系值

  • 正确关键词的概率计算为：
  • ⏺$p=sigmoid(uh),当word=w^{\ast }$时
  • uh表示中间向量h和关键词的参数向量u的点乘，得到的是一个数值
  • 这样，当我们要提高p值时，就可以表示为尽可能提高正确关键词的概率

• 错误关键词（word=$\tilde{w}$)：最好能尽可能降低上下文与错误关键词的关系值

  • 错误关键词的概率计算为：
  • $p=sigmoid(uh),当word=\tilde{w}$时,$l(w)=1$
  • 但是，考虑到我们能够用一个函数式，表示同一个优化方向，即用函数式的极大值，来表示正确关键词概率的提升和错误关键词概率的降低。
  • 因此，我们可以不直接用错误关键词的概率直接计算，而是用下列概率参与计算：
  • ⏺$p=1-sigmoid(uh),当word=\tilde{w}$时,$l(w)=0$
  • 这样，当我们要提高p值时，就可以表示为尽可能降低错误关键词的概率

• 一个上下文与某个关键词的概率计算，就可以统一为：

  • $p=sigmoid(uh{)}^{l(w)}\ast (1-sigmoid(uh){)}^{(1-l(w))}$
    

• 一个上下文与所有关键词的概率计算，可以使用连乘$\prod$，把所有关键词与该上下文的概率乘起来

  • $P_{一个上下文}={\prod }_{w\in D}p={\prod }_{w\in D}sigmoid(uh{)}^{l(w)}\ast (1-sigmoid(uh){)}^{(1-l(w))}$
  • 相当于把每一列的p值相乘

• 所有上下文与所有关键词的概率计算，可以再增加一个连乘$\prod$，把所有关键词与所有上下文的概率乘起来

  • $P={\prod }_{所有上下文}{P}_{一个上下文}={\prod }_{所有上下文}{\prod }_{w\in D}sigmoid(uh{)}^{l(w)}\ast (1-sigmoid(uh){)}^{(1-l(w))}$
  • 相当于把整个MxN矩阵里的每一个p值相乘

• 为了更好的计算梯度，可以采用对数来进行求导迭代

  • $P_{final}=lnP=ln{\prod }_{所有上下文}{\prod }_{w\in D}p={\Sigma }_{所有上下文}{\Sigma }_{w\in D}[l(w)\ast ln(sigmoid(uh))+(1-l(w))\ast (1-ln(sigmoid(uh)))]$

  • 由此可以分别对每一个参数向量u求偏导，不是同一个u的偏导为0，因此可去掉${\Sigma }_{w\in D}$
    

  • $\frac{əP_{final}}{u_i}=\frac{ə{\Sigma }_{所有上下文}[l(w)\ast (1-sigmoid(u_{i}h))+(1-l(w))\ast (-ln(sigmoid(u_{i}h)))]}{u_i}$

  • 整理可得：$\frac{əP_{final}}{u_i}={\Sigma }_{所有上下文}[l(w)-sigmoid(u_{i}h)]h$

  • 同理，可对每一个中间向量h求偏导，不是同一个h的偏导为0，因此可直接去掉${\Sigma }_{所有上下文}$

  • $\frac{əP_{final}}{h_j}=\frac{ə{\Sigma }_{w\in D}[l(w)\ast (1-sigmoid(u{h}_j))+(1-l(w))\ast (-ln(sigmoid(u{h}_j)))]}{h_j}$

  • 整理可得：$\frac{əP_{final}}{h_j}={\Sigma }_{w\in D}[l(w)-sigmoid(u{h}_j)]u$

• 然后每一个关键词的参数向量u和每一个上下文的特征参数向量w，都会进行迭代

  • $u^{new}=u_i+\eta ({\Sigma }_{所有上下文}l(w)-sigmoid(u_{i}h))h$
    • ————需要迭代N个关键词
  • $w_{ci}^{new}=w_{ci}+\eta ({\Sigma }_{w\in D}[l(w)-sigmoid(u{h}_j)])u$,$w_{ci}是指上下文中的每一个单词的特征向量$
    • ————需要迭代M个上下文里的每一个单词特征参数向量
    • 即（M*2c个单词的特征参数向量w需要迭代）
  • 因为对h求导，h是上下文中的每一个单词的特征参数向量w之和，因此可以直接让每一个单词的特征参数向量w都以相同的迭代梯度（即h的偏导数）进行迭代
    

4. 反向传播-计算

对输出层的参数U，求梯度进行迭代
对投影层的参数W，求梯度进行迭代

对构造出的极大似然估计法里边的每一个u进行求偏导，计算出迭代式

再对每一个上下文的中间向量h求偏导，得到h的梯度，再去计算W的迭代式

这个过程其实跟HierarchicalSoftmax模型是差不多的，因此直接进入HierarchicalSoftmax的梳理！

⭐【基于HierarchicalSoftmax模型下的CBOW模型】流程

• 输出层：
  • 将词典D里的每个单词，按词频构建成huffman树，树的每个非叶子节点有一个θ参数向量
  • 再根据sigmoid函数分别计算从根节点到每个叶子节点的概率值$\widehat{y_1}$、$\widehat{y_2}$、$\widehat{y_3}$、$\widehat{y_4}$、$\widehat{y_5}$…$\widehat{y_N}$
  • 将对数似然函数作为损失函数$Loss=(1-y\ast )ln(1-\hat{y})+y\ast ln\hat{y}$，来计算出从根节点到叶子节点的损失值
    

反向传播过程：

• 输出层：迭代huffman非叶子节点上的θ参数
  • 求出θ的梯度值，进行θ迭代
• 投影层：迭代W矩阵权重系数
  • 求出W的梯度值，进行W迭代

1. 构建huffman树

首先，huffman树是什么？

已经有非常优秀的博主教学了，直接照搬照抄为上策。

至于怎么构建，也有非常优秀的博主做了很生动的教学讲解，一个字：抄！
NLP重铸篇之Word2vec:huffman树构造

2. 计算huffman树的路径概率

huffman树的作用，其实是将投影层中得到的中间向量$h$，从huffman树的根节点开始，逐层进行二分类，直到分到真实的预测关键词$y^{\ast }$
这样，当通过训练得到一棵huffman树后，实际用来预测时，就会根据huffman树来预测关键词
要想让预测的结果更准确，那就需要让预测到真实关键词的概率P提高到最大。
而预测到真实关键词之前，需要经过层层二分类，那就相当于每次二分类选择正确路径的概率都尽可能提高
那么每次二分类的概率要怎么衡量呢？
光有中间向量$h$是不够的，我们还需要维护每个节点的一个参数向量θ，根据$h$和θ的线性关系，来作为下一个节点的概率表示，具体要如何表示呢，需要先了解huffman树的相关参数和函数

而在CBOW模型中，是将词典D中的每一个单词，按照词频来构建一棵huffman树。
并且，huffman树是有参数θ的，这个参数θ一开始由我们初始化设定，后续反向传播时，再迭代更新。
具体整个huffman树的参数如下：

d：

• 表示每个节点的编码，根节点没有编码，因此d1为无
• 左子树为𝑑_𝑙𝑒𝑓𝑡=1，右子树为𝑑_right =1- 𝑑_𝑙𝑒𝑓𝑡 =0

θ：表示每个非叶子节点的参数向量，向量元素与特征元素个数相同（即θ也是3×1的向量），主要用于表示在不同分裂节点中，h向量所对应的特征的权重值表示
θ和中间向量h的乘积$h^T\theta$，最终是一个数值，这个数值进行sigmoid函数运算后，用于表示选择下一个节点的概率（用sigmoid函数来表示）

• 规定如下：
  下一个节点选左子树的概率p为 $1-sigmoid(h^T\theta )$
  下一个节点选右子树的概率p为 $sigmoid(h^T\theta )$
• 但为了避免区分左右节点的概率公式计算，可以将左右节点的概率计算统一为
  $p=(1-d_{下个节点left})(1-sigmoid(h^T\theta ))+d_{下个节点right}sigmoid(h^T\theta )$
  • 当下个节点选择左子树时，$d_{下个节点}=1$，$p=1-sigmoid(h^T\theta )$
  • 当下个节点选择右子树时，$d_{下个节点}=0$，$p=sigmoid(h^T\theta )$
  • 那么无论下一个节点选择的是左子树还是右子树，都可以用一个式子来表示其概率
  • 即 $p=(1-sigmoid(h^T\theta ){)}^{(1-d_{下个节点})}\ast sigmoid(h^T\theta {)}^{d_{下个节点}}$
    

另外，
$pat{h}^{\ast }$，表示从从根节点走到带预测关键词$y^{\ast }$的路径
$l^{\ast }$，表示从根节点走到待预测关键词$y^{\ast }$的路径，所经过的总节点数

那么最终的$P=p_1\ast p_2...p_{l^{\ast }-1}={\prod }_{i=2}^{l^{\ast }}(1-sigmoid(h^T{\theta }_{i-1}{)}^{(1-d_i)}\ast sigmoid(h^T{\theta }_{i-1}{)}^{d_i}$

即，$P={\prod }_{i=2}^{l^{\ast }}[(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}{)}^{(1-d_i)}\ast {\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}}^{d_i}]$，$\prod$是连乘符号

以上是单个上下文预测正确的概率

3. 计算预测概率

我们要让单个上下文的预测正确概率P尽可能达到最大，但连乘下的P求极值，比较复杂

因此可以使用对数函数，在不改变其单调性情况下，求极值，并将连乘变为累加

即将求$P$的极值，转化为求$lnP$的极值

$lnP=ln{\prod }_{i=2}^{l^{\ast }}[(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}{)}^{(1-d_i)}\ast {\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}}^{d_i}]$

$={\Sigma }_{i=2}^{l^{\ast }}[(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}]$

这只是单个上下文的预测概率求极值的表示

但这还不够，我们还要同时考虑所有上下文的预测概率，因此为了综合提升整个模型的相关参数W和θ

每个上下文，都可以求出一个P值，通过对单个上下文的P值进行huffman参数θ的迭代和W特征权重系数的迭代，使得模型对单个上下文的训练效果得到强化
W特征权重系数这个还比较简单，因为每个上下文中的多个背景单词，都有唯一对应的特征权重系数向量
但θ却不一样，因为θ是huffman树上非叶子节点上的参数，而huffman树是全局唯一的树，也就意味着每个叶子节点上的θ也是全局的，这意味着一个θ会对多个上下文产生影响，相应的多个上下文都可能会对一个非叶子节点上的θ产生影响。
因此，基于huffman树上的θ参数对多个上下文有影响的情况下，需要思考以下问题：

• P是对单个节点上的θ求偏导，但为了避免一个上下文的P对θ迭代后，另一个上下文的P对这个θ又再次迭代，导致θ优化的方向与前一个上下文不符合（就好像是，我把空调调到24度适合我睡觉，但你为了自己舒服又把空调调到28度，我就变得不舒服了）
  因此，应采取多个上下文同时对θ产生一次迭代即可。（大家协商好后，再调个合适的空调温度）
  当我们同时训练多个上下文时，会产生多个P，那么要同时衡量多个上下文的训练效果，这多个P是累加还是累乘，才能表示多个上下文的训练效果呢？
  • 累乘

但由于我们采用了对数，来对整体的P进行不改变单调性的求极值，因此累乘在对数函数的改造后，就变成了累加

我们需要同时将所有上下文的预测概率加和，综合进行优化迭代

将所有上下文的概率值加和，其实可以用${\Sigma }_{word\in c}$来简单表示

这是看公式时，对${\Sigma }_{word\in c}$含义的猜测
但如果是我猜测的意思，那我觉得${\Sigma }_{word\in c}$的表示，还是不够恰当的
因为word既然表示待预测的关键词，但关键词是有重复的，但关键词重复不代表上下文重复
我们是要加和所有上下文的预测正确概率，那${\Sigma }_{word\in c}$并不代表所有上下文
不过，先暂时这么着吧

即最终要提升的总概率值为
P = ${\Sigma }_{word\in c}{\Sigma }_{i=2}^{l^{\ast }}[(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}]$

CBOW模型反向传播

基于矩阵-输出层：迭代U

基于矩阵的CBOW的输出层，是对矩阵U，这个表示上下文和关键词关系权重的参数矩阵，进行迭代

类似于对θ的迭代，因此直接看θ的迭代。

基于huffman树-输出层：迭代θ

hierarchicalsoftmax模型是基于huffman树构建的，它的反向传播，主要是通过P总概率值，对参数进行求偏导

我们要让P达到极大值，那就沿着梯度的方向，迭代参数

整个模型中，有两个参数，一个是投影层的W，另外一个是矩阵U或huffman树上的θ

对θ求偏导，是对非叶子节点上的每一个θ变量求偏导，那么其他非叶子节点的θ求偏导为0，因此对累加符号${\Sigma }_{i=2}^{l^{\ast }}$即可消掉（因为非该节点上的θ，求偏导均为0）

按理来说，最终求出的偏导应该要保留${\Sigma }_{word\in c}$这个累加符号，这是所有上下文的累加表示，最终的偏导应该是这样的
$\frac{əP}{ə{\theta }_{i-1}}=\frac{ə{\Sigma }_{word\in c}{\Sigma }_{i=2}^{l^{\ast }}[(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}]}{ə{\theta }_{i-1}}={\Sigma }_{word\in c}(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})h$

但是！！！网上的推导，都是直接去掉了θ的两个累加符号，我非常不李姐！！！！！

$\frac{əP}{ə{\theta }_{i-1}}=\frac{ə[(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}]}{ə{\theta }_{i-1}}=(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})h$

因此θ的更新公式，可以写为 ${\theta }_{i-1}^{new}={\theta }_{i-1}+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})h$

注：这里的${\theta }_{i-1}$是对每个上下文的每个非叶子节点上的θ

η是提前设置好的学习率

投影层：迭代W

看看P的原式子，P = ${\Sigma }_{word\in c}{\Sigma }_{i=2}^{l^{\ast }}[(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}]$

式子里根本没有W，要怎么求W的偏导进行迭代呢？

其实，W最终会影响到中间向量h：$h=W^{T}X$，因此，可以让P先对h求偏导，再让h的偏导数称为W的迭代元素

$\frac{əP}{əh}=\frac{ə\Sigma word\in c{\Sigma }_{i=2}^{l^{\ast }}[(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}]}{əh}$

对θ和对h求偏导稍有不同，对于同一个上下文，它们的h都是一致的，因此属于同一个上下文贯穿的path路径上的h偏导，不为0，需保留累加同一个上下文huffman路径下的累加符${\Sigma }_{i=2}^{l^{\ast }}$。

但对于不是同一个上下文的h，是不同的，因此不属于同一个上下文的h偏导为0，所以可以去掉上下文的累加符$\Sigma word\in c$，

所以最终$\frac{əP}{əh}={\Sigma }_{i=2}^{l\ast }(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}){\theta }_{i-1}$

注：这里的$h$是对每个上下文的各特征之和的偏导

参考word2vec的数学原理详解

可知，h是同一个上下文里不同单词的各特征分别之和，因此要让不同的单词的不同特征进行迭代，只需将h的偏导数同时作用于各个单词的特征向量上。最终每个上下文里的单词，对应的词向量W 的迭代式子为

$W_{上下文词1}^{\ast }=W_{上下文词1}^{\ast }+\eta {\Sigma }_{i=2}^{l\ast }(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}){\theta }_{i-1}$
$W_{上下文词2}^{\ast }=W_{上下文词1}^{\ast }+\eta {\Sigma }_{i=2}^{l\ast }(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}){\theta }_{i-1}$
$W_{上下文词3}^{\ast }=W_{上下文词1}^{\ast }+\eta {\Sigma }_{i=2}^{l\ast }(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}){\theta }_{i-1}$
$W_{上下文词4}^{\ast }=W_{上下文词1}^{\ast }+\eta {\Sigma }_{i=2}^{l\ast }(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}){\theta }_{i-1}$

周末看这些东西，比较痛苦。。。还是上班摸鱼的时候再看吧

【矩阵】VS【HierarchicalSoftmax】

这俩的区别，用一张图，简单认识

未解的困惑

还有几个待思考的问题：

• 为什么θ的偏导，去掉了两个累加【重点】
• ${\Sigma }_{word\in c}$的含义，究竟是所有上下文，还是所有关键词？
• 为什么换用huffman树后，会节省计算
• 为什么迭代终止条件没有明确，是一次性就迭代好了吗？不可能，因为有学习率，应该是一步步迭代的
• 为什么偏导一定是极大值，有没有可能是极小值呢？

困惑1：为什么θ的偏导，去掉了两个累加？

先来解决第一个问题：为什么θ的偏导，去掉了两个累加？

众里寻他千百度，就是没人具体说明那两个累加符号的含义，以及求偏导后，为什么要舍弃
后来转念一想，想明白了
嗷。。。可能是太简单了。。。别人压根就不屑于解释。。。

其实去掉了两个累加，和我原想的保留一个累加，迭代的方式不同，但最终结果是一样的

按理来说，最终求出的偏导应该要保留${\Sigma }_{word\in c}$这个累加符号，这是所有上下文的累加表示，最终的偏导应该是这样的
$\frac{əP}{ə{\theta }_{i-1}}=\frac{ə{\Sigma }_{word\in c}{\Sigma }_{i=2}^{l^{\ast }}[(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}]}{ə{\theta }_{i-1}}={\Sigma }_{word\in c}(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})h$

这种情况下，对于整个huffman树某个节点的${\theta }_{i-1}$而言，${\Sigma }_{word\in c}$是将所有上下文经过这个θ的偏导数都求和了，因此只需对这个节点的${\theta }_{i-1}$进行一次迭代，代表了同时受所有上下文的影响。

即${\theta }_{i-1}={\theta }_{i-1}+\eta {\Sigma }_{word\in c}(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})h$

但很多文章都是去掉了${\Sigma }_{word\in c}$累加符，这是因为它们是单独对单个上下文对应的某个huffman节点θ进行求偏导，
即原本P的计算式里是有两个累加符号的
$P={\Sigma }_{word\in c}{\Sigma }_{i=2}^{l^{\ast }}[(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}}]$

但为了计算方便，将$P_{i-1}^{\ast }=(1-d_i)ln(1-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})+d_{i}ln\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}}$

$P_{i-1}^{\ast }$代表的是关键词为*的上下文，在huffman树上的第$i-1$个节点上的概率值。

$P_{i-1}^{\ast }$对${\theta }_{i-1}^{\ast }$求偏导，得到的是没有累加符号的$(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$

则${\theta }_{i-1}^{\ast }$的迭代公式为${\theta }_{i-1}^{\ast }={\theta }_{i-1}^{\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$

但这是单个上下文*，对huffman上第$i-1$个节点上的θ迭代，即${\theta }_{i-1}^{\ast }$

如果有20个上下文，分别对huffman上第$i-1$个节点上的θ迭代，相当于要迭代20次，

那么就是
第一个上下文对${\theta }_{i-1}^{\ast }$的迭代：${\theta }_{i-1}^{1\ast }={\theta }_{i-1}^{\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$
第二个上下文对${\theta }_{i-1}^{\ast }$的迭代：${\theta }_{i-1}^{2\ast }={\theta }_{i-1}^{1\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$
第三个上下文对${\theta }_{i-1}^{\ast }$的迭代：${\theta }_{i-1}^{3\ast }={\theta }_{i-1}^{2\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$
第四个上下文对${\theta }_{i-1}^{\ast }$的迭代：${\theta }_{i-1}^{4\ast }={\theta }_{i-1}^{3\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$
…
第二十个上下文对${\theta }_{i-1}^{\ast }$的迭代：${\theta }_{i-1}^{20\ast }={\theta }_{i-1}^{19\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$

最终${\theta }_{i-1}^{\ast }$的迭代值，其实是所有上下文的累加${\theta }_{i-1}^{20\ast }={\theta }_{i-1}^{\ast }+\eta {\Sigma }_1^{20}(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$

那么，假设所有的上下文累加用${\Sigma }_{word\in c}$表示，那么${\theta }_{i-1}^{\ast }$的迭代就可以写成我原本设想的那样
${\theta }_{i-1}={\theta }_{i-1}+\eta {\Sigma }_{word\in c}(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})h$

因此，对于θ的不同迭代式，只是迭代的方式不同，但本质结果是一致的：

• 所有上下文同时迭代：${\theta }_{i-1}={\theta }_{i-1}+\eta {\Sigma }_{word\in c}(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})h$
• 每个上下文依次迭代：${\theta }_{i-1}^{\ast }={\theta }_{i-1}^{\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$

但这里要考虑一个非常现实的问题：不同的上下文，可能对应路径上的θ是不同的
我们应该对同一路径下（同一个关键词）的上下文偏导数进行累加，才能得到正确的θ值
因为，如果是不同路径，那么有可能会求不到偏导数，比如boy路径下，就无法对θ3进行求偏导
因此，我原本设想的${\theta }_{i-1}={\theta }_{i-1}+\eta {\Sigma }_{word\in c}(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}})h$，实现起来比较困难，因为还要加一层判断，判断某个上下文路径上，是否有该θ，才能进行累加，这太麻烦了
不如原本人家公式里来的简单，就是对每个上下文对应的huffman上的每个θ，依次进行迭代
所以，还是遵照前人的公式，会更好！！！！！！

• 每个上下文依次迭代：${\theta }_{i-1}^{\ast }={\theta }_{i-1}^{\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$
  

困惑2： ${\Sigma }_{word\in c}$的含义，究竟是所有上下文，还是所有关键词？

这个问题，原本很困惑，众里寻他千百度，也没有答案
百度百度，当初为啥不叫千百度呢

实际上，${\Sigma }_{word\in c}$表示的是所有关键词，但它对迭代θ和W，毫无影响

当我们迭代某个θ值时，${\Sigma }_{word\in c}$对迭代结果无影响：${\theta }_{i-1}^{\ast }={\theta }_{i-1}^{\ast }+\eta (1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}^{\ast }}})h$

但当我们迭代W时，${\Sigma }_{word\in c}$也没有产生影响，因为

$W^{\ast }=W^{\ast }+\eta {\Sigma }_{i=2}^{l\ast }(1-d_i-\frac{1}{1+e^{-h^T\ast {\theta }_{i-1}}}){\theta }_{i-1}$

困惑3：为什么换用huffman树后，会节省计算？

这就要跟原本不用huffman树的方法作对比了

原本不用huffman树时，是采用了一个参数矩阵$U$的方式，来保存每个待预测关键词word与上下文的关系数据。

我们知道，投影层的中间向量h，表示的是上下文单词向量的三个特征数据分别之和，形状为3x1

而所有的上下文中间向量h，构成一个3xM的H矩阵

而要衡量上下文与每一个待预测的关键词之间的关系，需要一个参数矩阵$U$

参数矩阵$U$里的一个向量u中含有3个值，这三个值实际表示的是对中间向量h的特征1、特征2、特征3的权重系数，而u和h的点乘得到的单个值，实际上就是待预测的关键词与上下文的特征之和h的关系表示。

相当于，如果有一个上下文简称为context1的中间向量为h1，那么这个中间向量与哪个待预测的关键词关系最大呢？

这就需要我们让h1和所有关键词的向量u，逐一进行点乘

context1与第一个关键词的关系：值1 = h1u1
context1与第二个关键词的关系：值2 = h1u2
context1与第三个关键词的关系：值3 = h1u3
context1与第…个关键词的关系：
context1与第N个关键词的关系：值N = h1uN

这时得到的N个值，需要通过softmax函数来衡量，softmax(值)最大的，即为关系最大的待预测关键词。

那么，有M个上下文，每个上下文的中间向量h有3个特征值，因此，M个上下文构成的中间矩阵H为Mx3

而待遇测的关键词有N个，每个关键词都有3个值表示向量h的3个特征值的权重值，因此，U矩阵为Nx3

$U^{T}M$的结果是一个N×M的矩阵，N行M列，每一列表示每个上下文与N个上下文的值

要对$U^{T}M$的每一列，进行softmax计算，得到N个值，而每一列都要进行进行N次softmax计算，因此计算总次数为M×N次，语料库非常大的情况下，计算量也会非常大

而如果采用hierarchicalsoftmax的huffman树，每个上下文只需与每条路径下的θ值进行一次计算，那每条路径下总共的θ值是远远小于N的，理想状态下是一个均衡满二叉树的huffman，那么每个关键词的路径上总共有多少个θ，取决于这个均衡满二叉树有多少层，这个层数的计算，其实就是$lo{g}_{2}N$

所以，M个上下文分别与$lo{g}_{2}N$个进行计算，计算量为M×$lo{g}_{2}N$

所以hierarchicalsoftmax的huffman树的计算量M×$lo{g}_{2}N$，与原始的矩阵U的计算量M×N，可谓是大大减少了啊！

困惑4：为什么迭代终止条件没有明确，是一次性就迭代好了吗？

百度不得其解，我是否可以把P值不再改变作为终止条件，应该可以吧

困惑5：为什么偏导一定是极大值，有没有可能是极小值呢？

唉。。。不知道鸭，是不是还要证明矩阵是半正定啥啥啥的。。。
我对半正定这个东西，还没理解呢唉
学了个寂寞属于是
先暂时理解到这吧，已经非常透彻了，很透彻了
嗷，我后来觉得，应该是跟对数似然函数本身就是一个凸函数有关吧
不管了

以后有时间，再试着自己搞个程序看看效果