模型可解释性 DeepLIFT 论文解析

黄金贵

已于 2022-11-29 14:46:18 修改

阅读量4.7k

点赞数 3

分类专栏：模型可解释性文章标签：深度学习人工智能

于 2022-11-29 12:11:06 首次发布

本文链接：https://blog.csdn.net/weixin_50396183/article/details/128034297

版权

模型可解释性专栏收录该内容

1 篇文章 0 订阅

订阅专栏

论文标题：Learning Important Features Through Propagating Activation Differences

论文作者：Avanti Shrikumar, Peyton Greenside, Anshul Kundaje

论文发表时间及来源：Oct 2019，ICML

论文链接：http://proceedings.mlr.press/v70/shrikumar17a/shrikumar17a.pdf

DeepLIFT方法

1. DeepLIFT理论

DeepLIFT解释了目标输入、目标输出与“参考(reference)”输入、“参考”输出间的差异。“参考”输入是人为选择的中性的输入。

用 $x_{i}$ 表示单层神经元或多层神经元的集合， $x^{0}$ 为 $x_{i}$ 对应的“参考”，有 $\Delta x_{i}=x_{i}-x^{0}$ 。用 $t$ 表示目标输入经过 $x_{i}$ 的输出（当 $x_{i}$ 为全部神经元的集合时， $t$ 为目标输出）， $t^{0}$ 表示“参考”输出，有 $\Delta t=t-t^{0}$ 。如（1）式， $\Delta t$ 为各个输入贡献分数的加和。

$\sum_{i=1}^{n}C_{\Delta x_{i}\Delta t}=\Delta t\qquad(1)$

2. 乘数(Multiplier)与链式法则

$(multiplier)\quad m_{\Delta x\Delta t}=\frac{C_{\Delta x\Delta t}}{\Delta x}\qquad(2)$

乘数与偏导数类似：偏导数 $\frac{\partial t}{\partial x}$ 是指 $x$ 产生无穷小变化时， $t$ 的变化率；而乘数是指 $x$ 产生一定量的变化后， $t$ 的变化率。

$m_{\Delta x_{i}\Delta t}=\sum_{j}^{}m_{\Delta x_{i}\Delta y_{j}}m_{\Delta y_{j}\Delta t}\qquad(3)$

这里 $\Delta y_{j}$ 可理解为中间层的 $\Delta t$ 。给定每个神经元与其直接后继的乘数，即可计算任意神经元与目标神经元的乘数。

3. 定义“参考”

MNIST任务中，使用全黑图片作为“参考”。

CIFAR10任务中，使用原始图像的模糊版本能突出目标输入的轮廓，而全黑图片作为参考时产生了一些难以解释的像素。

DNA序列分类任务中，以ATGC的期望频率作为“参考”。即目标输入是四维的one-hot编码，“参考”输入是相同维度的ATGC期望频率。这里还有一种方法没有看懂，见Appendix J。

4. 区分正、负贡献

$\Delta y=\Delta y^{+}+\Delta y^{-}\qquad(4)$

$C_{\Delta y\Delta t}=C_{\Delta y^{+}\Delta t}+C_{\Delta y^{-}\Delta t}\qquad(5)$

当应用RevealCancel规则时，区分正、负贡献非常重要。

5. 分配贡献分数的规则

线性规则

用于Dense层，卷积层，不可用于非线性层。定义线性函数 $y=b+\sum_{i}^{}\omega _{i}x_{i}$ ，则 $\Delta y=\sum_{i}^{}\omega _{i}\Delta x_{i}$ 。

$\Delta y^{+}=\sum_{i}^{}1\left \{ \omega _{i}\Delta x_{i}> 0 \right \}\omega _{i}\Delta x_{i}=\sum_{i}^{}1\left \{ \omega _{i}\Delta x_{i}> 0 \right \}\omega _{i}\left \{ \Delta x_{i}^{+}+\Delta x_{i}^{-} \right \}\qquad(6)$

$\Delta y^{-}=\sum_{i}^{}1\left \{ \omega _{i}\Delta x_{i}< 0 \right \}\omega _{i}\Delta x_{i}=\sum_{i}^{}1\left \{ \omega _{i}\Delta x_{i}< 0 \right \}\omega _{i}\left \{ \Delta x_{i}^{+}+\Delta x_{i}^{-} \right \}\qquad(7)$

$C_{\Delta x_{i}^{+}\Delta y^{+}}=1\left \{ \omega _{i}\Delta x_{i}> 0 \right \}\omega _{i}\Delta x_{i}^{+}\qquad(8)$

$C_{\Delta x_{i}^{-}\Delta y^{+}}=1\left \{ \omega _{i}\Delta x_{i}> 0 \right \}\omega _{i}\Delta x_{i}^{-}\qquad(9)$

$C_{\Delta x_{i}^{+}\Delta y^{-}}=1\left \{ \omega _{i}\Delta x_{i}< 0 \right \}\omega _{i}\Delta x_{i}^{+}\qquad(10)$

$C_{\Delta x_{i}^{-}\Delta y^{-}}=1\left \{ \omega _{i}\Delta x_{i}< 0 \right \}\omega _{i}\Delta x_{i}^{-}\qquad(11)$

$m_{\Delta x_{i}^{+}\Delta y^{+}}=m_{\Delta x_{i}^{-}\Delta y^{+}}=1\left \{ \omega _{i}\Delta x_{i}>0 \right \}\omega _{i}\qquad(12)$

$m_{\Delta x_{i}^{+}\Delta y^{-}}=m_{\Delta x_{i}^{-}\Delta y^{-}}=1\left \{ \omega _{i}\Delta x_{i}<0 \right \}\omega _{i}\qquad(13)$

$if \Delta x_{i}=0\quad m=0.5\omega _{i}\qquad(13)$

公式有点复杂，举例说明。“参考”输入 $\left [ 0, 0 \right ]\cdot \left [ 3, 4 \right ]^{T}=0$ ，目标输入 $\left [ 1, 2 \right ]\cdot \left [ 3, 4 \right ]^{T}=11$ ，则由式（6）得 $\Delta y^{+}=(1-0)*3+(2-0)*4=11$ ，由式（8）得 $\left [ 1, 2 \right ]$ 两个特征贡献分数分别为3和8，由式（12）得两个神经元的乘数分别为3和4。乘数的作用是，如果神经网络有两层线性函数， $\left [ 3, 4 \right ]^{T}$ 为第一层神经元， $\left [ 5 \right ]$ 为第二层神经元，则第二层的乘数为5，由式（3）得整个神经网络第一个特征的乘数为15，第二个特征的乘数为20，每个位置的输入乘以乘数就是其贡献分数。

Rescale规则

用于非线性层，如ReLU，tanh或sigmoid等。由于非线性函数 $y=f\left ( x \right )$ 只有一个输入，则 $C_{\Delta x\Delta y}=\Delta y$ ， $m_{\Delta x\Delta y}=\frac{\Delta y}{\Delta x}$ ， $\Delta y^{^{+}}$ 和 $\Delta y^{^{-}}$ 分别为：

$\Delta y^{^{+}}=\frac{\Delta y}{\Delta x}\Delta x^{^{+}}=C_{\Delta x^{^{+}}\Delta y^{^{+}}}\qquad(14)$

$\Delta y^{^{-}}=\frac{\Delta y}{\Delta x}\Delta x^{^{-}}=C_{\Delta x^{^{-}}\Delta y^{^{-}}}\qquad(15)$

$m_{\Delta x^{+}\Delta y^{+}}=m_{\Delta x^{-}\Delta y^{-}}=m_{\Delta x\Delta y}=\frac{\Delta y}{\Delta x}\qquad(16)$

当 $x\rightarrow x^{0}$ 时， $m_{\Delta x\Delta y}$ 可用梯度代替。Rescale规则解决了梯度饱和问题和值域问题，例子见论文。

RevealCancel规则

这里说明为何 $\Delta y^{^{+}}$ 和 $\Delta y^{^{-}}$ 需分开计算。下图是一个计算最小值的操作，假定 $i_{1}^{0}=i_{2}^{0}=0$ ，目标输入 $i_{1}=3$ ， $i_{2}=1$ ，则 $h_{1}=(3-1)=2>0$ ， $h_{2}=max(0, h_{1})=2$ 。根据线性规则，可知 $C_{\Delta i_{1}\Delta h_{1}}=i_{1}=3$ ， $C_{\Delta i_{2}\Delta h_{1}}=-i_{2}=-1$ 。根据Rescale规则， $m_{\Delta h_{1}\Delta h_{2}}=\frac{\Delta h_{2}}{\Delta h_{1}}=1$ ， $C_{\Delta i_{1}\Delta h_{2}}=m_{\Delta h_{1}\Delta h_{2}}C_{\Delta i_{1}\Delta h_{1}}=i_{1}=3$ ， $C_{\Delta i_{2}\Delta h_{2}}=m_{\Delta h_{1}\Delta h_{2}}C_{\Delta i_{2}\Delta h_{1}}=-i_{2}=-1$ 。则 $i_{1}$ 总贡献分数为 $C_{\Delta i_{1}\Delta o}=\Delta i_{1}m_{\Delta i_{1}\Delta o}=\Delta i_{1}(1+m_{\Delta i_{1}\Delta h_{1}}m_{\Delta h_{1}\Delta h_{2}}m_{\Delta h_{2}\Delta o})=0$ ， $i_{2}$ 总贡献分数为 $C_{\Delta i_{2}\Delta o}=\Delta i_{2}m_{\Delta 2_{1}\Delta o}=\Delta i_{2}m_{\Delta i_{2}\Delta h_{1}}m_{\Delta h_{1}\Delta h_{2}}m_{\Delta h_{2}\Delta o}=1$ 。

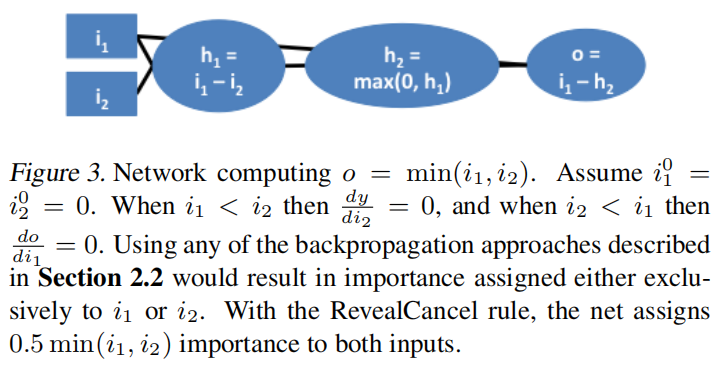
同样地，梯度，输入*梯度方法也会赋予其中一个特征0的贡献分数，这忽略了特征间的相互依赖性。 $\Delta y^{^{+}}$ 和 $\Delta y^{^{-}}$ 分开计算的公式为：

$\Delta y^{+}=\frac{1}{2}(f(x^{0}+\Delta x^{+})-f(x^{0}))+\frac{1}{2}(f(x^{0}+\Delta x^{-}+\Delta x^{+})-f(x^{0}+\Delta x^{-})) (17)$

$\Delta y^{-}=\frac{1}{2}(f(x^{0}+\Delta x^{-})-f(x^{0}))+\frac{1}{2}(f(x^{0}+\Delta x^{+}+\Delta x^{-})-f(x^{0}+\Delta x^{+}))(18)$

$m_{\Delta x^{+}\Delta y^{+}}=\frac{C_{\Delta x^{+}\Delta y^{+}}}{\Delta x^{+}}=\frac{\Delta y^{+}}{\Delta x^{+}}; m_{\Delta x^{-}\Delta y^{-}}=\frac{\Delta y^{-}}{\Delta x^{-}}\qquad(19)$