元器件基础学习笔记——电容定义、特性和基本参数

一、电容的定义及计算

1.1 电容的定义

        电容是电路中的一种基本元件，用于存储电荷和能。它是指在给定电压下，电容器所带电量Q与电容器两极间的电压U的比值，叫电容器的电容。电容的单位是法拉（F）。

1.2 电容的计算公式

1.2.1 电容的定义式

        电容的定义式是通过电容器的性质和电场的概念推导得到的。根据电场的定义，电场强度E等于电场中的电荷量Q与电场中的电势差V之比，即：

E = Q / V

        在电容器中，当施加电压时，正极和负极之间会形成电场，导致正极和负极之间产生电势差。根据电场的性质，我们可以得到电容的定义式：

C = Q / U

        C—表示电容，单位是法拉（F）

        Q表示导体上的电荷量，单位是库仑（C）

        U表示导体上的电势差，单位是伏特（V）

1.2.2 电容的决定式

        电容的决定式是通过电容器的几何形状和介质特性来确定的。根据电容器的结构和材料，可以得到不同类型的电容器，如平行板电容器、球形电容器、圆柱形电容器等。

1.2.2.1 平行板电容器

        平行板电容器由两块平的金属板构成，中间通过绝缘介质（如空气或者电介质）隔开。其中一块金属板带有正电荷，另一块金属板带有等量的负电荷，形成了电场。

        对于一个平行板电容器，其决定式可以表示为：

C = ε0 * εr * A / d

        C—表示电容，单位是法拉（F）

        εr—表示介质的相对介电常数，表示物质相对于真空的电场效应能力

        ε0—表示真空中的介电常数（ε0＝8.854187817 × 10-12F/m，近似值）

        A—表示电容器的极板面积，单位是平方米（m²）

        d—表示极板之间的距离，单位是米（m）

        实际介电常数（Dielectric Constant，简称Dk，通常用符号εr表示）

        实际介电常数是指物质在电场中的响应力，也称为相对介电常数或相对电容率。它是一个无量纲的物理量，用εr表示。实际介电常数描述了物质在电场中相对于真空的电容性质。

        实际介电常数可以通过以下公式计算得到：

εr = ε/ε0

        因此上述平行板电容器的决定式也可以简化为：

C = ε * A / d

        常见材料的介电常数如下图：

        多层板电容器的电容计算

        多层板电容器是由多个层状的金属电极和绝缘层交替堆叠而成。以下图为例：

        现在我们有五块板连接到一根引线 （A），四块板连接到另一根引线 （B）。然后连接到引线 B 的四块板的两侧都与电介质接触，而连接到 A 的每个外板只有一侧与电介质接触。那么如上所述，每组板的有用表面积仅为8，因此其电容计算公式为：

C = 8 * ε * A / d

1.2.2.2 球形电容器

        球形电容器由两个形导体构成，中间通过绝缘介质隔开。其中一个球形导体为正极，另一个球形导体作为负极，而绝缘介质则起到隔离两个导体的作用。

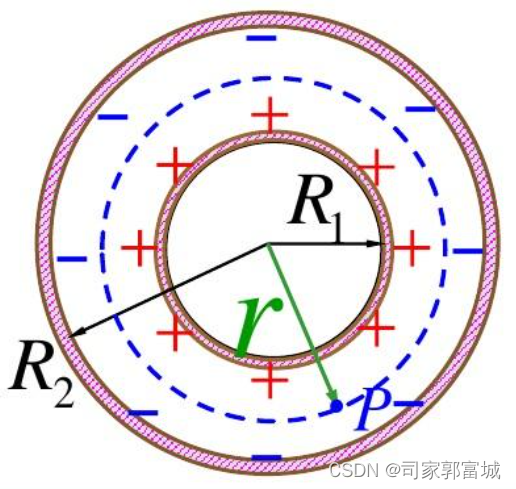
        对于一个球形电容器，其决定式可以表示为：

C=4πεR1R2/（R2-R1）

        R1—球形电容器的内半径，单位是米（m）

        R2—球形电容器的外半径，单位是米（m）

1.2.2.3 圆柱形电容器

        圆柱形电容器由两个平行的金属圆柱体构成中间通过绝缘材料（如空气或介质）隔开。其中一个金属圆柱体作为正极（称为内极），另一个金属圆柱体作为负极（称为外极）。两个金属圆柱体之间的空间形成电场，用于存储电荷。

        对于一个球形电容器，其决定式可以表示为：

C = (2πεl) / ln(RB/RA)

        l—表示圆柱长度，单位是米（m）

        RA—圆柱电极外径，单位是米（m）

        RB—圆柱电极内径，单位是米（m）

二、电容的特性

2.1 电容有储存电荷的能力

        当电容器连接到电源时，正极板上的电荷会被推入电容器，而负极板上的电荷则会被吸引到电源。这样，电容器内部就会储存起电荷。充放电过程如下图所示：

        时间常数τ

        电容充放电时间常数是指电容器在充电或放电过程中所需的时间，用于描述电容器充放电速度的快慢，它表示电容器充电或放电至其初始值的63.2%所需的时间。时间常数取决于电容器的电容值以及与之并联的电阻值。公式如下：

τ = R * C

        τ—电容充放电时间常数，单位是秒（s）

        R—电路中的电阻值，单位是欧姆（Ω）

        C—电路中的电电值，单位是法拉（F）

        电容两端电压与充放电时间的关系（估算时）可以参考下图：

        电容上积蓄的能量

        电容器在充放电过程中可以积蓄能量。电容器充电时，电荷从电源流入电容器，电场能量被存储在电场中。当电容器放电时，电荷从电容器流出，电场能量被释放出来。

2.2 阻直流，通交流

        电容器的电极被电介质阻隔，施加直流电压后，在充电过程中电流瞬间流过导线，但不会流到电介质的内部。即在两块板之间的非导电介质不能使两种电荷相互转移并接触，完成电荷流动。简单的说，主要是因为板间没有可导电物质，直流电才无法通过。这就是我们常说的隔直流。

        连接交流电源，则电极板周期性地反复进行充电与放电，电场方向也会相应地发生改变。虽然不是在绝缘体内部出现电子移动，但实际上与流过交流电流相同，因此可视为电容器使交流电流通过，从而使得电容器可以传递交流信号。相对于通常的电流（传导电流），我们将该电流称为位移电流。

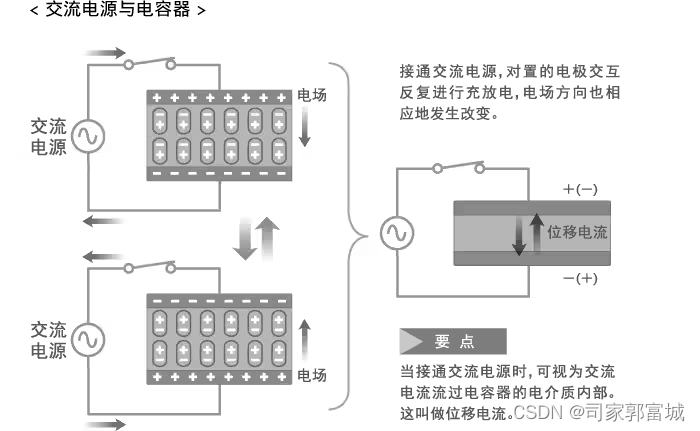
        交流电下理想电容电流超前电压90°

        电流与电压的相位关系是，电流超前电压90°，或电压落后电流90°。电容器电流超前电压90°的条件：

        ① 交流电源：使用交流电源作为电容器的电压源，因为交流电源的电压是周期性变化的。

        ② 纯电容负载：电容器是纯电容负载，没有其他元件（如电阻或感性元件）与之并联或串联。

        电容器的电流与电压之间存在以下关系：

i(t) = C * du(t) / dt

        i(t)—表示时间t时刻的电流

        C—表示电容器的电容量

        u(t)—表示时间t时刻的电压

        du(t)/dt—表示电压随时间的变化率。

        这个公式可以解释为：电流的大小与电容器的电容量以及电压随时间的变化率成正比。当电压变化率较大时，电流也会相应增大；当电压变化率较小或为零时，电流也会减小或为零。

        当加在电容两端的电压为 u = Umsinωt = U√2sinωt 时，可得电容电路的电流为：

i = Imsin(ωt+90°) = I√2sin(ωt+90°)

        交流电下，理想电容电压与电流波形如下图所示：

        从上面的波形中，我们可以看到电流领先电压 1/4 个周期或 90 个周期。

三、电容的参数

1.3.1 额定电压

        额定电压定义为可连续施加于电容器的最大电压。额定电压通常以直流电压（DC）或交流电压（AC）表示，单位为伏特（V）。当交流电压叠加在直流电压上时，峰值到峰值或零到峰值，以两者中较大者为准，应用时应保持电容两端的电压在额定电压范围内。

1.3.2 耐压

        耐压也称为电容介质耐电强度，是指在满足一定条件下的最大可承受电压，长时间超过这个电压工作，就很有可能导致电容损坏。

        通常，电容器的耐压是以额定电压的倍数来表示。具体倍数取决于电容器的类型和规格。一般来说，电解电容器的耐压通常是额定电压的1.5倍到2倍，而固体电解电容器的耐压通常是额定电压的2倍到3倍。而对于其他类型的电容器，如陶瓷电容器和聚合物电容器，耐压通常是额定电压的2倍到5倍。

        下图是murata一款贴片电容手册中给出的耐压参数，并注明了相应的测试条件：

1.3.3 绝缘电阻和漏电流

       因为电容器的电极之间是绝缘的，所以理论上电阻值是无穷大的。然而，在实际应用中，由于电容极板间的介质材料并非绝对绝缘，总会有少量电流通过这些区域，形成所谓的漏电流。这种不完全的绝缘特性导致电容表现出一定的电阻，这个电阻被称为绝缘电阻。

        当直流电压直接施加在电容器后，突入电流（也称充电电流）的流量如下图所示。随着电容器逐渐被充电，电流呈指数降低。

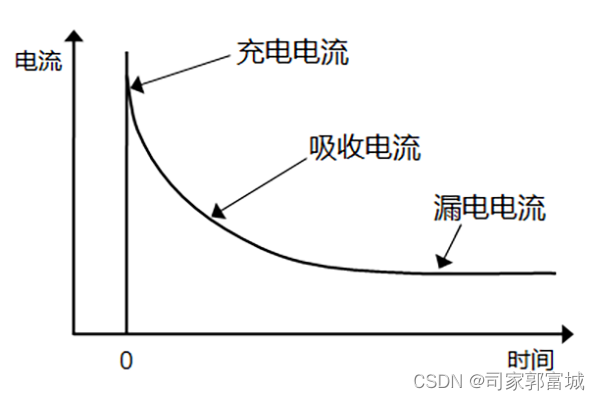
        电流I(t)随时间的增加而分为三类，即充电电流Ic(t)、吸收电流Ia(t)和漏电电流Ir，公式如下：

I(t) = Ic(t) + Ia(t) + Ir

        充电电流表明电流通过一个理想的电容器。与充电电流相比，吸收电流有一个延迟过程，并且在低频范围内伴随有介电损耗、造成高介电常数电容器（铁电性电容器）极性相反并在陶瓷与金属电极界面上发生肖特基障垒。

        漏电电流是在吸收电流的影响降低后，在一定阶段出现的常数电流。因此，下述电流值随施加在电容器上的时间电压量而变化。这意味着，只有在指定电压用途下的定时测量才能确定电容器的绝缘电阻值。 

        绝缘电阻的单位表示为电阻［MΩ］或CR乘积［MΩ･F］。CR乘积［MΩ･F］是标称电容和绝缘电阻的乘积，例如：CR产品为500Ω･F或更高，电容为1μF时绝缘电阻 500ΩF/1μF＝500MΩ。

        绝缘电阻越大表明直流电压下的漏电电流越小。一般情况下，绝缘电阻值越大，电路的准确性越高。

1.3.4 损耗角、损耗角正切值、品质因数

        电容等效模型

        理想电容模型假设电容器是一个完全理想的元件，没有任何损耗和内阻。它只有一个参数——电容值（C），用来表示电容器的存储能量的能力。

        实际电容模型考虑了电容器的内部损耗和结构特性，通常由ESR（等效串联电阻）、C、ESL（等效串联电感）组成，如下图所示：

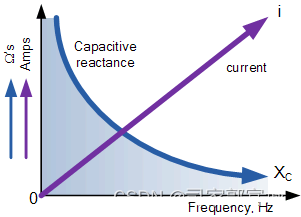
        容抗

        容抗是电容器对交流电的阻抗，用符号Xc表示，单位是欧姆（Ω）。容抗的计算公式如下：

Xc = 1 / (2πfC)

        f—表示交流电的频率，单位是赫兹（Hz）

        C—表示电容器的电容值，单位是法拉（F）

        从上面的容抗公式可以看出，如果频率或电容中的任何一个要增加，则总容抗会降低。当频率接近无穷大时，电容器的电抗将降低到零，就像一个完美的导体。，当频率接近零或直流时，电容器的电抗将增加到无穷大，就像一个非常大的电阻。容抗与频率的关系如下图所示：

        损耗角δ（Dissipation Factor）

        损耗角δ是指电容器内部的能量损耗与电容器存储的能量之间的相位。它是一个无量纲的角度，通常用度（°）表示。理想状况下，电路上不存在电容器内部的能量消耗，但实际上，电容器的介电损耗、电极、导线、电极的电阻成分（ESR：等效串联电阻）都会引发能量损耗。这以流过电容器的电流的相移进行表示。损耗角δ越大，表示电容器内部的能量损耗越大。

        损耗角正切值tanδ（Tangent of Loss Angle）

        以三角函数tan（正数）表示该滞后的角度（损耗角）δ，称为tanδ或介质损耗角正切值。它是一个无量纲的值，通常用小数表示。tanδ越大，表示电容器内部的能量损耗越大。

         tanδ可以通过以下公式计算得出：

tanδ = ESR / |Xc| = 1/2πfRC

        损耗角正切值tanδ的计算不包含ESL部分的损耗，是因为ESL主要与电感成分相关，而不是与能量损耗。在计算tanδ时，一般只考虑电阻性损耗，如果需要更准确地描述材料或元件的损耗特性，可以考虑同时考虑ESL和电阻性损耗的影响。（一般厂家给出的规格书中，损耗角都是在120Hz条件下的。120Hz频率较低，感抗很小，可以忽略。）

        品质因数（Quality Factor）

        电容的品质因数也称为Q值，描述了电容器在储存和释放能量时的损耗程度，即能量储存效率的高低。Q值越低，表示电容器的能量储存效率越低，损耗越大。

        Q值可以通过以下公式计算得出：

Q = 1/tanδ = 2πfRC

1.3.5 电容的温度特性

        电容的温度特性是指电容器在不同温度下的电容值变化情况。一般来说，电容的温度特性可以分为两种情况：正温度系数和负温度系数。

        ① 正温度系数：当电容器的电容值随着温度的升高而增加时，称为正温度系数。这种情况下，电容器的电容值会随着温度的升高而增大。

        ② 负温度系数：当电容器的电容值随着温度的升高而减小时，称为负温度系数。这种情况下，电容器的电容值会随着温度的升高而减小。

        电容的温度特性要受到以下几个因素的影响：

        ① 介质特性：不同的介质对温度的响应不同，导致电容器的温度特性也不同。例如，铝电解电容器通常具有负温度系数，而陶瓷电容器通常具有正温度系数。

        ② 电解液：对于铝电解电容器来说，其电解液的性质也会对温度特性产生影响。不同的电解液会导致不同的温度特性。

        ③ 结构设计：电容器的结构设计也会对温度特性产生影响。例如，电容器的内部结构和材料的选择都会对温度特性产生影响。

        ④ 工作条件：电容器在不同的工作条件下，如电压、频率等，其温度特性也可能会有所变化。

        常用的滤波电容为瓷介质电容，瓷介质电容器有超稳定型：COG或NPO，稳定型：X7R，和通用型：Y5V或Z5U三种。不同介质的电容器的温度特性如下图所示：

        

        从图中可以看到，COG电容器的容量几乎随温度没有变化，X7R电容器的容量在额定工作温度范围变化12%以下，Y5V电容器的容量在额定工作温度范围内变化70%以上。这些特性是必须注意的，否则会出现滤波器在高温或低温时性能变化而导致设备产生电磁兼容问题。

　　COG介质虽然稳定，但介质常数较低，一般在10～100，因此当体积较小时，容量较小。X7R的介质常数高得多，为2000 ～ 4000，因此较小的体积能产生较大的电容，Y5V的介质常数最高，为5000 ～ 25000。

　　在选用电容器时，注意不要片面追求电容器的体积小，这种电容器的介质虽然具有较高的介质常数，但温度稳定性很差，这会导致设备的温度特性变差。

1.3.6 电容的直流偏压特性

        陶瓷电容器的静电容量还会因所施加的电压而发生变化，在直流电压下被称为直流偏压特性，多用于电子设备的积层陶瓷电容器。

        根据电介质的种类大致分为低电容率类(种类1)与高电容率类(种类2)，并根据温度特性进一步细分。温度特性由JIS（日本工业标准）与EIA（美国电子工业协会）标准规定。

        陶瓷是由众多晶粒(grain)构成的多晶体。在强电介质中，晶畴(domain)的自发极化是朝着向不同的方向，相互抵消，整体不表现出自发极化。但是，如果所施加的直流电场的强度增高，则最初自发极化的朝向会定向为电场的朝向，电容率增大。如果进一步提高电场，则会终止定向，达到饱和状态，电容率降低。因此，在施加直流偏压的情况下，需要考虑到电介质的特性、使用电压与耐圧从而进行选择。此外，存在这样的趋势，即越是小型尺寸的电容器，因直流偏压所引发的静电容量的减少越大。

1.3.7 电容的阻抗-频率特性

        电容的阻抗-频率特性是指电容器在交电路中的阻抗随频率变化的规律。实际电容的阻抗可以用以下公式表示：

        电容器具有频率交流越高越易通过的性质。理想的电容器随着频率增高，阻抗会无限接近于零，但是在现实的电容器中，阻抗会以某个频率为临界升高。因此，阻抗-频率特性呈V字型(或U字型)曲线。这是因为电容器所具有的ESL (等效串联电感)与电容器之间形成了LC 谐振电路。

        与V字曲线的底部相对应的频率叫做自谐振频率(SRF)，在该频率以下都作为电容器发挥作用，在此以上的频率范围内则作为电感器发挥作用。

        电容的自谐振频率

        电容的自谐振频率是指在特定电容值和电感值下，电容与电感之间的振荡频率。当电容与电感串联时，形成一个谐振回路，当外加交流信号的频率等于自谐振频率时，谐振回路会发生共振现象。计算公式如下：

        

        对于电容的自谐振频率，一般来说并没有直接的危害，但在实际应用中需要注意以下几点：

        ① 电压过高：当电路中的电容达到自谐振频率时，会导致电压在电容上升高，可能会超过电容的额定电压，从而引发电容击穿或破坏

        ② 电流过大：在自谐振频率附近，电路中的电感和电容会形成共振回路，导致电流增大。如果电流过大，可能会对电路中其他元件产生不良影响，如损坏其他元件或引起过热等问题

        ③ 信号失真：自谐振频率附近的信号可能被增强或衰减，可能导致信号失真或系统不稳定

        为了避免或减小电容的自谐振带来的不良影响，可以采取以下几种方法：

        ① 选择合适的电容器：选择具有较高自谐振频率的电容器，使其自谐振频率远高于实际工作频率。这样可以确保在实际工作频率下，电容器的阻抗仍然较大，不会引起共振现象

        ② 添加阻尼电阻：在电容器的并联或串联位置添加适当的阻尼电阻，可以增加电路的阻尼，减小共振幅值。这样可以有效地抑制自谐振现象

        ③ 使用多个电容器并联：将多个电容器并联使用，可以增加总的等效电容量，从而提高自谐振频率。通过合理选择并联电容器的数值和数量，可以使自谐振频率远高于实际工作频率，避免自谐振问题