主成分分析（PCA）及葡萄酒数据集示例代码

是远阿_

已于 2023-11-01 14:20:26 修改

阅读量679

点赞数 3

文章标签： python

于 2023-11-01 10:19:28 首次发布

本文链接：https://blog.csdn.net/weixin_50684911/article/details/134147391

版权

一、主成分分析的主要步骤

主成分分析（PCA）是一种无监督的线性变换技术，广泛地应用于不同的领域，特别是特征提取和降维。他的应用领域包括股票市场交易的探索性数据分析和去噪，以及生物信息学的基因组数据和基因表达水平分析。

PCA帮助我们根据特征之间的相关性来识别数据中的模型。PCA旨在寻找高维数据中存在的最大方差的方向，并将数据投影到维度小于或等于原始数据的新子空间。假设新特征轴彼此正交，该空间的正交轴（主成分）可以解释为方差最大的方向，如下图所示。其中x1、x2为原始特征轴，而PC1和PC2为主成分方向。

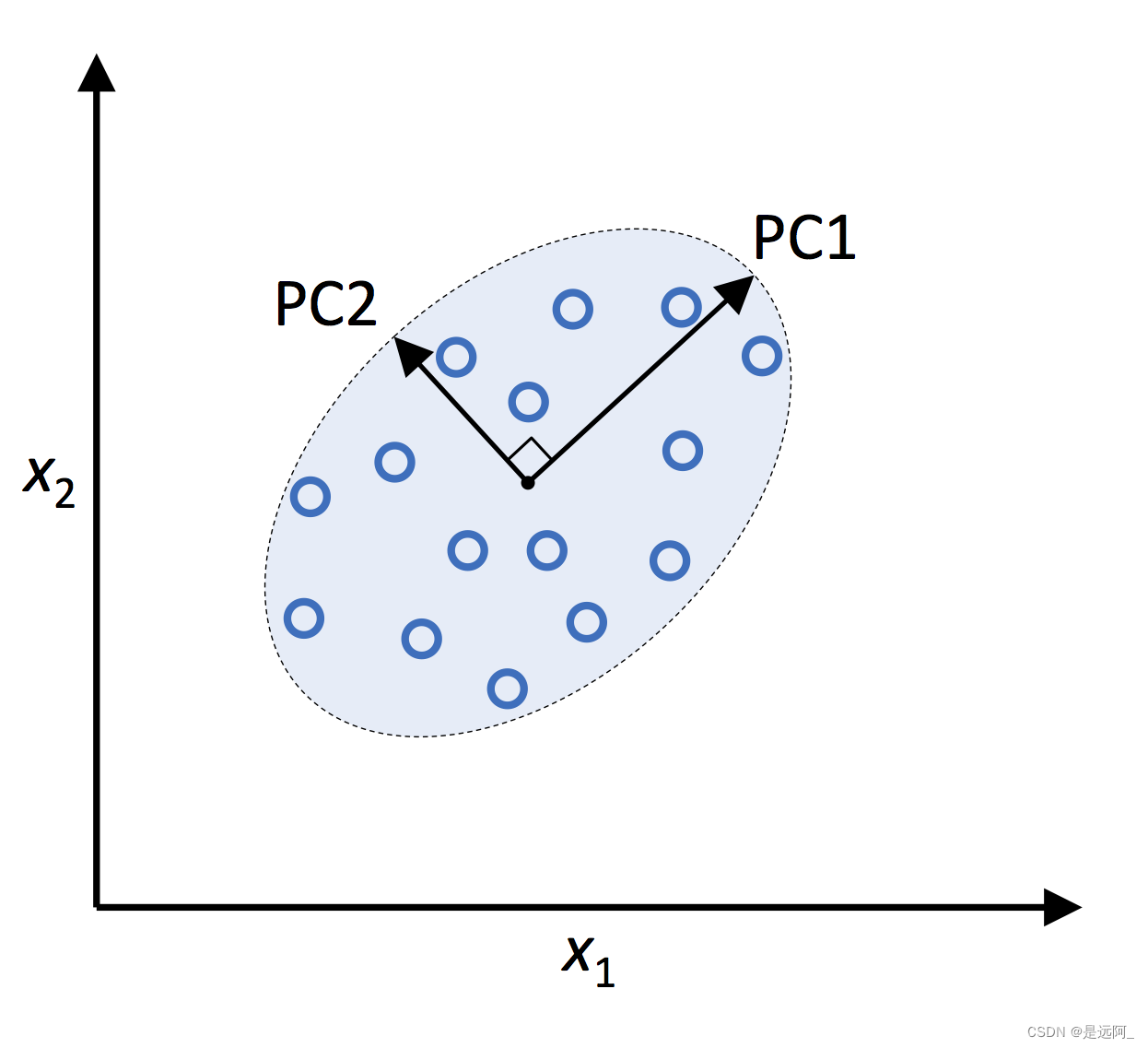
如果用PCA降维，我们可以构建d $\times$ k维的变换矩阵W，它能把训练样本的特征向量x映射到新的k维特征子空间，该空间的维数比原来的d维特征空间要少。
例如，假设我们有一个特征向量x：

$x=[x_{1,}x_{2... ,} x_{d}],x\in \mathbb{R}^{d}$
接着通过一个变换矩阵 $W\in \mathbb{R}^{d\times k}$ 进行变换：

$xW=z$

结果以向量方式表达如下：

$z=[z_{1,}z_{2,}...,z_{k}], z\in \mathbb{R}^{k}$
在原高维数据转换到k维新子空间（通常k≤d）的结果中，第一主成分的方差最大。另外，PCA 的方向对数据尺度非常敏感，需要在进行PCA之前对特征进行标准化。

假设我们只取一个主成分，则 $w\in R^{d\times 1}$ ，该主成分为 $z=xw$ ， $x\in \mathbb{R}^{1\times d}$

$var(z)=var(xw)=w^{T}cov(x)w=w^{T}\Sigma w$

因为 $\Sigma$ 为正定阵，所以有分解 $\Sigma =Q\Lambda Q^{T}$ ，其中 $Q$ 为单位对称矩阵， $\Lambda$ 中的特征值降序排列。于是又有：

$var(z)=w^{T}\Sigma w=w^{T}Q\Lambda Q^{T}w$

取 $w$ 为 $\Sigma$ 的最大特征根 $\lambda _{1}$ 对应的特征向量 $q_{1}$ ， $q_{1}\in \mathbb{R}^{d\times 1}$ ，则有：

$var(z)=w^{T}Q\Lambda Q^{T}w=q_{1}^{T}Q\Lambda Q^{T}q_{1}=\lambda _{1}$ $(q_{1}^{T}q_{i}=0,i=2,...d)$

同理，若取两个主成分分析，有 $w_{2}=q_{2}$ ，第二个主成分 $z_{2}=xq_{2}$

此时， $var(z+z_{2})$ 是最大的，且 $var(z+z_{2})=\lambda _{1}+\lambda _{2}$

基于此可构造： $w=[q_{1},q_{2}]$

PCA步骤简单概括如下：
1）标准化d维数据集。
2）构建协方差矩阵。
3）将协方差矩阵分解为特征向量和特征值。
4）以降序对特征值排序，从而对相应的特征向量排序。
5）选择对应k个最大特征值的k个特征向量，其中k为新特征子空间的维数（k≤d）。
6）由前k个特征向量构造投影矩阵W。
7）用投影矩阵W变换d维输入数据集X以获得新的k维特征子空间。

二、提取主成分

以下讨论 PCA 的前四个步骤：
1）标准化数据集。
2）构建协方差矩阵。
3）获取协方差矩阵的特征值和特征向量。
4）以降序対特征值排序，从而对特征向量排序。

首先，加载葡萄酒数据集。

import pandas as pd

df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/'
                      'machine-learning-databases/wine/wine.data',
                      header=None)

df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
                   'Alcalinity of ash', 'Magnesium', 'Total phenols',
                   'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
                   'Color intensity', 'Hue',
                   'OD280/OD315 of diluted wines', 'Proline']

df_wine.head()

按照7：3的比例划分训练集、测试集，标准化为单位方差。

from sklearn.model_selection import train_test_split

X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values

X_train, X_test, y_train, y_test = \
    train_test_split(X, y, test_size=0.3, 
                     stratify=y,
                     random_state=0)

from sklearn.preprocessing import StandardScaler

sc = StandardScaler()  #标准化
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)

然后，构造协方差矩阵。

其中，特征 $x_{j}$ 和 $x_{k}$ 之间的整体协方差计算公式如下：

$\sigma _{jk }=\frac{1}{n}\sum_{i=1}^{n}(x_{j}^{(i)}-\mu _{j})(x_{k}^{(i)}-\mu _{k})$

特征向量v满足以下条件：

$\Sigma v=\lambda v$

$\lambda$ 是特征值。

调用Numpy的linalg.eig函数来获得葡萄酒数据集协方差矩阵的特征向量和特征值。

import numpy as np
cov_mat = np.cov(X_train_std.T)  #计算标准化训练集的协方差矩阵
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)   #用np.linalg.eig完成特征分解

print('\nEigenvalues \n%s' % eigen_vals)   #eigen_vals特征值

产生13个特征向量eigen_vals，及对应的特征向量储存在13 $\times$ 13维矩阵eigen_vecs的列中。

三、总方差和解释方差

因为我们要降低维度，所以要找出前k个最重要的特征向量。在这之前，先把特征值的方差解释比计算出来。特征值 $\lambda _{j}$ 的方差解释比就是 $\lambda _{j}$ 与特征值总和之比：

方差解释比 = $\frac{\lambda _{j}}{\sum_{j=1}^{d}\lambda _{j}}$

调用Numpy的cumsum函数，可以计算出解释方差和，然后使用Matplotlib的step函数绘图。

tot = sum(eigen_vals)  #计算特征值的总和
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]  #计算每个特征值所占的方差解释比例
cum_var_exp = np.cumsum(var_exp) #对方差解释比例进行累积求和

import matplotlib.pyplot as plt


plt.bar(range(1, 14), var_exp, alpha=0.5, align='center',
        label='Individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid',
         label='Cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()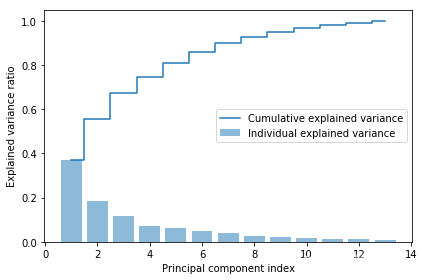

结果表明，第一主成分本身占方差的40%左右，前两个主成分合起来可解释数据集中几乎60%的方差。

四、特征变换

在把协方差矩阵分解为特征向量之后，接着完成最后的三个步骤，将葡萄酒数据集变换到新的主成分轴。

其余的步骤如下：
5）选择与前k个最大特征值对应的k个特征向量，其中k为新特征子空间的维数（k≤d）。
6）用前k个特征向量构建投影矩阵W。
7）用投影矩阵W变换d维输入数据集X以获得新的k维特征子空间。

把特征向量按特征值降序排列，从所选的特征向量构建投影矩阵，用投影矩阵把数据变换到低维子空间。
把特征向量按特征值降序排列：

eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
               for i in range(len(eigen_vals))]   #将每个特征值的绝对值与对应的特征向量组成一个元组。

eigen_pairs.sort(key=lambda k: k[0], reverse=True)
#通过lambda k: k[0]指定按照元组中的第一个元素进行排序，reverse=True表示降序排列。

收集对应前两个最大特征值的特征向量，从数据集中捕获大约60%的方差。这里只选择两个特征向量来进行说明。

w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
               eigen_pairs[1][1][:, np.newaxis]))
#eigen_pairs[0]表示第一个特征值-特征向量对，eigen_pairs[0][1]表示该特征值对应的特征向量。通过[:, np.newaxis]将其转换为列向量。
#使用np.hstack()函数将这两个列向量水平拼接起来，形成投影矩阵W。
print('Matrix W:\n', w)
#每一列都是一个主成分

依据前两个特征向量创建一个13 $\times$ 2维的投影矩阵W。

用投影矩阵将x（表示13维的行向量）变换到PCA子空间（主成分1和2），从而获得x’，即由两个新特征组成的二维实例向量：

$x' =xW$

X_train_std[0].dot(w)  #X_train_std的第一条样本数据，使用投影矩阵W进行线性变换。

通过计算矩阵点积，将整个训练集变换成两个主成分：

$X'=XW$

X_train_pca = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']

for l, c, m in zip(np.unique(y_train), colors, markers):
    plt.scatter(X_train_pca[y_train == l, 0],    #属于标签为l的样本在第一和第二个主成分上的投影。
                X_train_pca[y_train == l, 1], 
                c=c, label=l, marker=m)

plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

可视化后，由散点图可以看出与第二主成分（y轴）相比，数据更多地沿着x轴（第一主成分）传播，与前面方差解释比的结论一致。

五、使用sklearn进行实现

计算13个解释方差比。

from sklearn.decomposition import PCA

pca = PCA()
X_train_pca = pca.fit_transform(X_train_std)
pca.explained_variance_ratio_  #每个方差比例

解释方差比可视化。

plt.bar(range(1, 14), pca.explained_variance_ratio_, alpha=0.5, align='center')
plt.step(range(1, 14), np.cumsum(pca.explained_variance_ratio_), where='mid')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')

plt.show()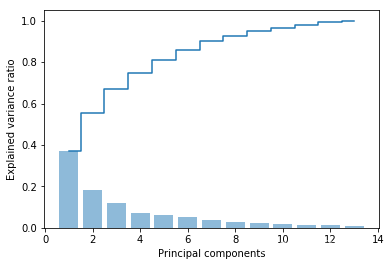

定义降维后维度并标准化。

pca = PCA(n_components=2)  #降维后的特征数为2
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)

plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1])
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.show()

PCA 是scikit-learn 的一个转换器类，我们首先用训练数据来拟合模型，然后用相同模型参数转换训练数据和测试数据。将PCA 类应用到葡萄酒训练数据集上，通过逻辑回归对转换后的样本进行分类，调用 plot_decision_regions函数实现决策区域的可视化。

from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, resolution=0.02):

    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])  #colors[:len(np.unique(y))] 的意思是根据类别数量选择对应数量的颜色。

    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1  #X[:, 0] 表示提取特征向量 X 的所有行（样本），并只保留第一个维度的数值。
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),  #x1_min 到 x1_max 步长为 resolution 的一维数组
                           np.arange(x2_min, x2_max, resolution))
    #np.meshgrid 函数生成一个二维的网格坐标矩阵。
    
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)  #将 xx1 和 xx2 的二维网格坐标矩阵展平为一维
    #利用分类器的 predict 方法对展平后的特征向量进行预测，得到对应的类别标签。对于每个网格点，都得到了一个预测值。
    
    Z = Z.reshape(xx1.shape)
    
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    for idx, cl in enumerate(np.unique(y)):  #表示对于每个唯一值 cl，使用变量 idx 来追踪它在数组中的索引
        plt.scatter(x=X[y == cl, 0], 
                    y=X[y == cl, 1],
                    alpha=0.6, 
                    color=cmap(idx),
                    edgecolor='black',
                    marker=markers[idx], 
                    label=cl)

from sklearn.linear_model import LogisticRegression

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)

lr = LogisticRegression(multi_class='ovr', random_state=1, solver='lbfgs')
lr = lr.fit(X_train_pca, y_train)

plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

训练数据的决策区域减少为两个主成分轴。

在测试数据集上同样绘制决策区域，可以得到样本的分类效果较好。

plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

将参数 n_components 设置为 None来初始化 PCA类，这样就可以保留所有的主成分，系统将返回排过序的所有主成分而不是进行降维。然后通过调用 explained_variance_ratio_属性访问解释方差比。

pca = PCA(n_components=None)
X_train_pca = pca.fit_transform(X_train_std)
pca.explained_variance_ratio_

是远阿_

关注

3
点赞
踩
12

收藏

觉得还不错? 一键收藏
2
评论
主成分分析（PCA）及葡萄酒数据集示例代码

主成分分析（PCA）是一种无监督的线性变换技术，广泛地应用于不同的领域，特别是特征提取和降维。他的应用领域包括股票市场交易的探索性数据分析和去噪，以及生物信息学的基因组数据和基因表达水平分析。PCA帮助我们根据特征之间的相关性来识别数据中的模型。PCA旨在寻找高维数据中存在的最大方差的方向，并将数据投影到维度小于或等于原始数据的新子空间。假设新特征轴彼此正交，该空间的正交轴（主成分）可以解释为方差最大的方向，如下图所示。其中x1、x2为原始特征轴，而PC1和PC2为主成分方向。
复制链接

扫一扫