48、Consistent Video Depth Estimation

简介

主页：https://roxanneluo.github.io/Consistent-Video-Depth-Estimation/

提出了一种从随机捕获的视频中估计时间相干和几何一致深度的系统。

传统的多视点立体方法，如COLMAP，通常会对移动的物体产生不完整的深度或纹理较差的区域。

基于学习的方法预测了每一帧的密集深度，但视频重建是闪烁的和几何不一致的。

论文视频深度估计是完全密集的，全局尺度一致的，并能够处理动态移动的物体，因此能添加视频特效。

论文提出一种算法，用于重建单目视频中所有像素的密集、几何一致的深度。利用传统的运动结构重建来建立视频像素的几何约束。与经典重构中的特殊先验不同，论文使用了基于学习的先验，即为单幅图像深度估计训练的卷积神经网络。在测试时，对这个网络进行微调，以满足特定输入视频的几何约束，同时保留它在受约束较少的部分视频中合成似是而非的深度细节的能力。

这种算法能够处理具有挑战性的手持捕获输入视频与支持少量的动态场景运动，如挥手，不能用于极端的物体运动。

深度视频质量和一致性的提高使得有趣的新应用成为可能，全自动视频特效与密集的场景内容相互作用

实现流程

将单目视频作为输入，为每一视频帧估计一个摄像机姿态以及一个密集的、几何一致的深度图(达到比例模糊度)。

几何一致性这一术语不仅意味着深度图不会随着时间的推移而闪烁，而且还意味着所有深度图都是相互一致的。因此，可以通过它们的深度和相机姿势在帧之间精确地投射像素，例如：一个静态点的所有观测都应该映射到世界坐标系中的一个公共3D点上，而不漂移

以单眼视频作为输入，采样了一对(可能很远的)帧，并使用预训练的单幅图像深度估计模型估计深度，以获得初始深度图。从这对图像中，使用光流和前后一致性检查建立对应关系。然后，利用这些对应关系和相机姿势提取三维几何约束。将三维几何约束分解为两个损失:1)空间损失和2)视差损失，并利用它们通过标准反向传播对深度估计网络的权重进行优化。这个测试时间训练强制网络在这个特定的视频的多个帧之间最小化几何不一致的错误。经过微调阶段，视频最终深度估计结果由微调模型计算。

PRE-PROCESSING

使用基于运动的结构和多视点立体重建软件COLMAP来估计N帧视频中的每一帧i的内部摄像机参数 $K_i$、外部摄像机参数($R_i,t_i$)以及半密集深度图$D_i^{MVS}$。对于没有定义深度的像素，将这些值设置为零。

由于动态对象在重构过程中经常会导致错误，应用Mask R-CNN 在每一帧中独立地分割出人(视频中最常见的“动态对象”)，并抑制这些区域的特征提取(COLMAP提供了这个选项)

SfM和基于学习的重构的尺度通常不匹配，因为这两种方法都是尺度不变的。这体现在两种方法生成的深度图的值范围不同。为了使尺度与几何损失兼容，调整了SfM尺度，因为可以通过将所有相机平移乘以一个因子来简单地做到这一点。

设 $D_i^{NN}$为基于学习的深度估计方法产生的初始深度图。首先计算图像 i 的相对比例为

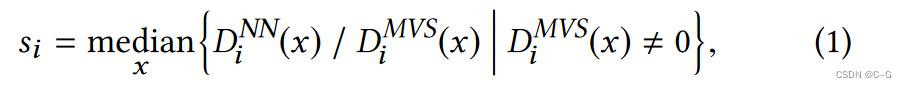
D(x) 为像素 x 处的深度

然后可以计算全局尺度调整因子 s

更新所有的camera translations

下一步，将计算特定帧对的密集光流。对于视频中所有的 O($n^2$)对帧，这一步的计算成本非常高。因此，使用一个简单的层次结构方案来修剪帧对集，直到O(N)。

层次结构的第一层包含所有连续的帧对

更高的级别包含越来越稀疏的帧采样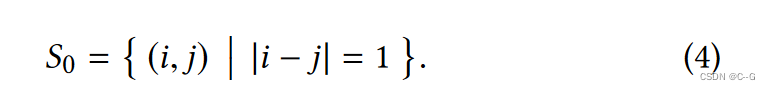
最后一组采样帧是所有级别的对的并集

对于 S 中的所有帧对 (i, j)，需要计算一个密集光流场 $F_{i\to j}$。因为当帧对尽可能对齐时，流量估计工作得最好

首先使用同源曲(用基于ransac的拟合方法计算)对齐(可能遥远的)帧，以消除两帧之间的主导运动(例如，由于相机旋转)。然后使用FlowNet2 计算对齐帧之间的光流。考虑到移动对象和遮挡/不遮挡(因为它们不满足几何约束或不可靠)，应用前后向一致性检查并删除前后向误差大于1像素的像素，生成一个二进制映射$M_{i\to j}$。此外，观察到对于重叠较少的帧对，流量估计结果并不可靠。因此，排除了|$M_{i\to j}$|小于图像面积20%的任何帧对。

TEST-TIME TRAINING ON INPUT VIDEO

对于给定的帧对 (i, j) ∈S，光流场 $F_{i\to j}$描述了哪些像素对显示相同的场景点。可以使用流来测试当前深度估计的几何一致性:如果流是正确的，且流移位的点$f_{i\to j}(x)$与深度重新投影的点$p_{i\to j}(x)$相同(下面定义了这两个术语)，那么深度必须是一致的。

可以把它变成一个几何损失 $L_{i\to j}$，并通过网络反向传播任何一致性误差，从而迫使它产生比以前更一致的深度。$L_{i\to j}$包含两个项，图像空间损耗 $L_{i\to j}^{spatial}$和视差损耗$L_{i\to j}^{difference}$。为了定义它们，首先讨论一些符号。

设 x 为坐标系i中的二维像素坐标，流位移点为

为了计算深度重投影点 $p_{i\to j}(x)$，首先使用摄像机的本征 $K_i$ 和当前的深度估计$D_i$，将2D坐标提升到帧i的摄像机坐标系中的3D点 $c_i(x)$，

其中，$\tilde{x}$为 x 的齐次增广。我们进一步将点投影到另一帧j的摄像机坐标系中，

最后把它转换回坐标系 j 中的像素位置，

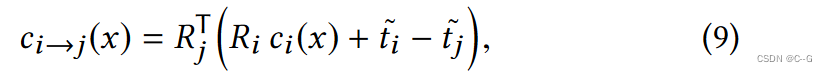
其中$\pi ([x,y,z{]}^T)=[\frac{x}{z},\frac{y}{z}]$
这惩罚了流位移点和深度重投影点之间的图像空间距离

视差损失同样对摄像机坐标系中的视差距离进行惩罚:

其中$U_I$是坐标系i的焦距，$z_i$和$z_{i\to j}$分别是$c_i$和$c_{i\to j}$的标量z分量。

因此，对流有效的所有像素的总体损失只是这两种损失的组合，

λ = 0.1是平衡系数。

效果