【408精华知识】并查集考点大总结！

一、定义

并查集(Union-find) 是一种数据结构，用于维护一些不相交的集合，支持合并两个集合以及判断两个元素是否属于同一个集合。

并查集可以使用树来实现，每个集合可以看做是一棵树，代表元素是根节点。使用路径压缩可以减少查找操作的时间复杂度，使用按秩合并可以减少合并操作的时间复杂度，使得并查集的时间复杂度可以达到近乎常数级别，因此在一些算法中广泛应用，比如 Kruskal 算法。

二、操作

1. 初始化：将每个元素初始化为单独的集合，每个集合的代表元素就是自己；
   把数组初始化为“-1”：
   

2. 查找：给定一个元素，找到它所属的集合的代表元素；
   不进行路径压缩，目的是找到结点的根结点：
   

3. 合并：将两个集合合并成一个集合，即将其中一个集合的代表元素作为另一个集合的代表元素的子节点。
   找到各自的祖先，将一个合并到另一个上边：
   

三、优化

1. 小树合并到大树：每次合并时都把小树合并到大树身上，就可以尽量让树不长高；
   

2. 路径压缩：查找谁就去压缩哪条路径；
   

总结：

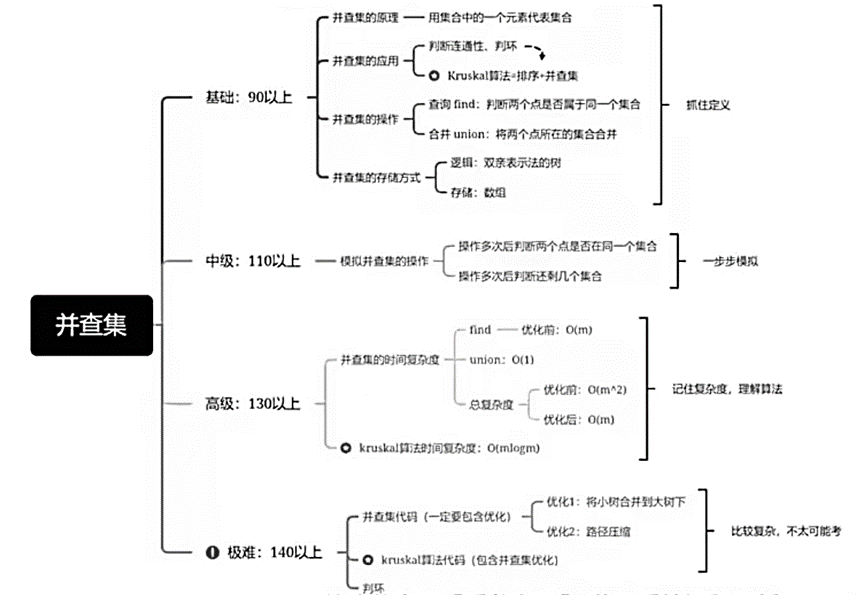
并查集的常见应用：
①克鲁斯卡尔算法求最小生成树；
②求无向图的连通分量；
③判断无向图的连通性。

注意，并查集不会用于迪杰斯特拉算法。

写在后面

这个专栏主要是我在学习408真题的过程中总结的一些笔记，因为我学的也很一般，如果有错误和不足之处，还望大家在评论区指出。希望能给大家的学习带来一点帮助，共同进步！！!

参考资料
[1]王道408教材（2025版）
[2]王道课程资料