RMQ维护区间最大值 O(nlogn)

AcWing 1273. 天才的记忆

Source：AcWing or 《信息学奥赛一本通》

从前有个人名叫 WNB，他有着天才般的记忆力，他珍藏了许多许多的宝藏。

在他离世之后留给后人一个难题（专门考验记忆力的啊！），如果谁能轻松回答出这个问题，便可以继承他的宝藏。

题目是这样的：给你一大串数字（编号为 1 到 N，大小可不一定哦！），在你看过一遍之后，它便消失在你面前，随后问题就出现了，给你 M 个询问，每次询问就给你两个数字 A,B，要求你瞬间就说出属于 A 到 B 这段区间内的最大数。

一天，一位美丽的姐姐从天上飞过，看到这个问题，感到很有意思（主要是据说那个宝藏里面藏着一种美容水，喝了可以让这美丽的姐姐更加迷人），于是她就竭尽全力想解决这个问题。

但是，她每次都以失败告终，因为这数字的个数是在太多了！

于是她请天才的你帮他解决。如果你帮她解决了这个问题，可是会得到很多甜头的哦！

输入格式
第一行一个整数 N 表示数字的个数。

接下来一行为 N 个数，表示数字序列。

第三行读入一个 M，表示你看完那串数后需要被提问的次数。

接下来 M 行，每行都有两个整数 A,B。

输出格式
输出共 M 行，每行输出一个数，表示对一个问题的回答。

数据范围
1≤N≤2×105,
1≤M≤104,
1≤A≤B≤N。

输入样例：

6
34 1 8 123 3 2
4
1 2
1 5
3 4
2 3

输出样例：

34
123
123
8

关于维护区间最大值有很多种解法，RMQ只能是离线操作，而线段树可以动态维护和查询，in a word ,
线段树可以支持边修改边查询，而RMQ只能生成ST表之后离线查询 这里先介绍RMQ算法 也就是 ST表 O(nlogn)

RMQ算法，实际上是基于动态规划预先处理数据，查询时时间复杂度是常数级。
f[i][j] 意思是从第i个开始长度为 2^j 区间中的最大值
那么f[i][j]的转移方程也就是 f[i][j] =max( f[i][j-1], f[i+2^(j-1)][j-1])

处理完ST表 接下来就是查询了

给定左边界l，右边界r 求区间最大值
首先我们可以确定区间长度len = r-l+1
设 2^k <= len
我们可以求出满足该条件的最大的k 那么 2 * 2^k >= len
然后取 max(f[l][k],f[r-2^k+1][k])

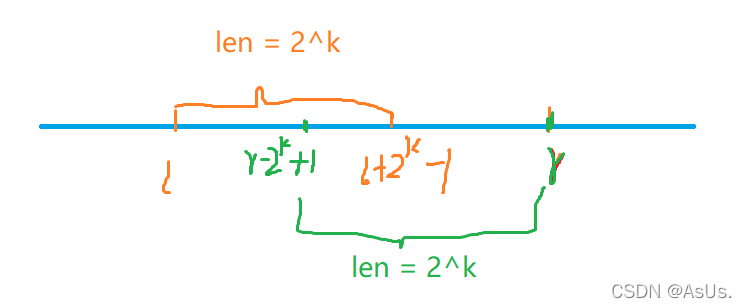
虽然可能有交叉但是两个子区间完全覆盖了父区间，取两子区间最大值即可

#include<bits/stdc++.h>
using namespace std;
const int N=200010,M=18;//取能覆盖题目最大范围的二进制M
int s[N];	
int n;
int f[N][M];
void RMQ(){
	for(int j=0;j<=M;j++){
		for(int i=1;i+(1<<j)-1<=n;i++){//i+(1<<j)-1<=n是因为右边界不能大于n
			if(!j) f[i][j]=s[i];//如果区间长度是1（2^0）那么该区间最大值就是这个数
			else f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
		}
	}
	return ;
}
int ask(int l,int r){
	int len=r-l+1;// 2^k<=len k<=log2(len)  
	//int mk=log(len)/log(2);换底公式
	int mk=log2(len);//直接求也未尝不可
	return max(f[l][mk],f[r-(1<<mk)+1][mk]);
}
int main(){
	//cout<<(1<<17);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>s[i]; 
	RMQ();
	int q;
	cin>>q;
	while(q--){
		int l,r;
		cin>>l>>r;
		cout<<ask(l,r)<<endl;
	}
	return 0;
}