多分类问题中评价指标F1-Score 加权平均权重的计算方法

多分类问题中评价指标F1-Score 加权平均权重的计算方法

    众所周知，F1分数（F1-score）是分类问题的一个衡量指标。在分类问题中，常常将F1-score作为评价分类结果好坏的指标。它是精确率和召回率的调和平均数，值域为[0,1]。
$$F_1=2\ast \frac{P\ast R}{P+R}$$
    其中，P代表着准确率（Precision），R代表召回率（Recall）。

1 准确率、召回率计算方法

介绍与二分类问题有关的常见几个变量概念。
    TP：实际为正类，预测为正类。
    FN：实际为正类，预测为负类。
    FP：实际为负类，预测为正类。
    TN：实际为负类，预测为负类。
$$P=\frac{TP}{TP+FP}R=\frac{TP}{TP+FN}$$
然而在多分类问题中，这些变量的概念有所改变。假设有{A,B,C}三个类别。
    TP：实际为A类，预测为A类。
    FN：实际为A类，预测为非A类。(也就是BC类)
    FP：实际为非A类，预测为A类。
    TN：实际为非A类，预测为非A类。
    针对多分类问题，首先需要构建一个真实结果和分类结果数据之间的列联表。举个例子：
    x={0,1,1,1,2,2} – 真实情况
    y={0,1,0,2,1,1} – 预测情况
   其列联表如下：

   
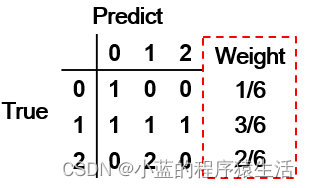
   TP = co.diag() = [1,1,0]
   FN = co.sum(axis=1)-TP = [0,2,2]
   FP = co.sum(axis=0)-TP = [1,2,1]
   TN=np.sum(co)-TP-FN-FP = [4,1,3]
   这是如果按照二分类方式计算F1分数的话，最终结果为一个向量。因此，需要对向量进行计算，本文主要介绍加权平均方法，其他方法较为简单，自行检索。
   加权平均的权重通过列联表中每行真实类别的数量除以变量长度计算出，即计算每行的和（axis=1）除以总长度。（见上图）
$$F_{1}weight=\frac{2PR}{P+R}\times weight=\frac{2}{3}\times \frac{1}{6}+\frac{1}{3}\times \frac{1}{2}+0\times \frac{1}{3}=0.2778$$