文章介绍了公平赌博的概念，通过一个硬币投掷的例子阐述了期望效用在决策中的作用。参与者会基于效用函数来判断是否接受赌博，这涉及到风险态度的三种类型：风险厌恶、风险中性和风险偏好。接着，文章讨论了在选择风险资产时如何利用效用函数的一阶导数来指导决策，并介绍了绝对风险系数和相对风险系数作为衡量厌恶程度的指标。
01案例引入：公平赌博
投掷一个硬币，head则获得1元，tail则失去1元。无论头还是尾，投掷到任意一个的概率为1/2，因此，总的期望值为0.
影响是否进入或者拒绝这个赌博的因素是参与者的效用。
如果参与者现在有5元，而他拒绝进入这个赌博的原因可以表示为：
u（5）>1/2u(6)+1/2u(4)
或者：u(6)-u（5）<u(5)-u(5-1)
简而言之，获得一块钱的期望效用小于失去一元钱的效用。
02期望效用函数
当我们使用期望效用函数这种偏好。我们需要考虑两个因素，第一个因素是所有可能出现的结果，第二个是出现这些结果的概率。
在这个理论中，状态独立，时间可加。
但事实上，一个情况发生时，我们需要考虑expected payoff(期望增益)和expected utility（期望效用）。
03 风险态度risk attitude
风险厌恶：risk aversion
风险中性：risk neutral
风险偏好：risk seeking
04 风险资产的选择
原理：在风险资产的份数为0时，查看效用函数的一阶导数的值，如果一阶导数>0,说明增加风险资产的份数，整体效用函数值上升，可以进行风险资产的投资。
05绝对风险系数和相对风险系数
绝对风险系数函数：
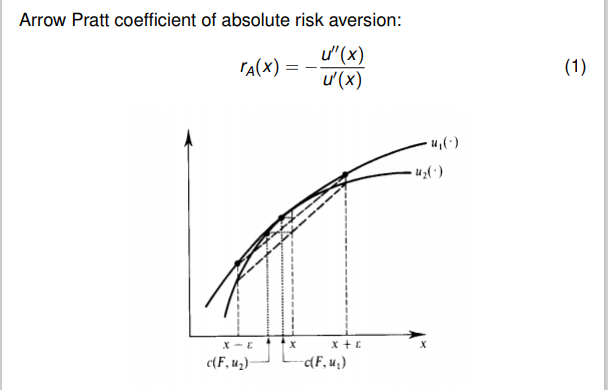
除以一阶导数：抵消效用函数一阶导后的常数值。一阶导函数图像弯曲程度越大，厌恶程度越大。
相对效用函数：
绝对效用函数，效用函数值是一个绝对的值。相对效用函数，期望回报占投入资产恒定比例。（存疑，不懂）
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
