使用Python实现DBSCAN聚类算法及可视化

目录

实战过程

数据准备

DBSCAN模型

聚类结果评估

可视化展示

运行结果

总结

---

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，可以发现任意形状的簇，并且能够在噪声数据的情况下不受干扰地识别出核心对象。本篇文章将介绍如何使用Python实现DBSCAN聚类算法及可视化。

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚类算法适用于以下情况：

1. 数据分布具有密度区别：对于密度高的数据点，会被分为一个簇；而对于密度低的数据点，会被认为是噪声点。

2. 数据分布多样化：DBSCAN能够发现任意形状的簇，不需要预先知道簇的数量和形状。

3. 噪声数据较多：DBSCAN能够正确区分噪声数据和有效数据，有效避免噪声数据对聚类结果的影响。

4. 聚类效果需求较高：相对于传统的K-Means聚类算法，DBSCAN能够处理复杂的非球形簇，并且具有更好的鲁棒性。

因此，如果在聚类任务中，数据分布具有明显的密度区别，且需要发现任意形状和数量的簇，同时希望聚类结果具有更好的鲁棒性，那么就可以考虑使用DBSCAN聚类算法。然而，对于高维度和高斯分布的数据，DBSCAN表现不如传统的聚类算法，并且需要合理设置参数才能得到好的聚类效果。

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚类算法的主要步骤如下：

1. 选择一个未访问的数据点作为起始点，找到该数据点的半径范围内的所有数据点。

2. 如果半径范围内的数据点数量大于等于阈值min_samples，则认为这些数据点属于同一个簇，并进行标记。如果数量小于阈值，则将该数据点标记为噪声点。

3. 对于半径范围内的所有数据点，递归地进行相同的操作，直到所有相邻的点都被访问。

4. 将未被访问的数据点作为起点，重复执行上述步骤，直到所有数据点都被访问。

5. 所有被标记为同一簇的数据点构成一个簇，所有未被标记的数据点构成噪声点。

6. 最终得到若干个簇和若干个噪声点，可以通过可视化方法来展示聚类结果。

需要注意的是，DBSCAN算法中的核心参数是半径范围内数据点的数量阈值min_samples和邻域半径eps。这两个参数的设置对于聚类效果具有重要影响，需要根据实际情况进行调整。同时，在处理高维度数据时，可以使用降维算法来减少数据的维度，提高聚类效率。

优点：

（1）能够发现任意形状的簇，对异常值的鲁棒性较好。

（2）不需要预先设置簇的数量。

（3）能够正确区分噪声数据和有效数据。

（4）相对于其他聚类算法，计算复杂度较低，容易实现。

缺点：

（1）结果可能受参数的选择影响，如eps和min_samples等。

（2）对于不同密度的簇效果并不完全一致，如高密度簇和低密度簇。

（3）在处理高维数据时，由于维数灾难的存在，可视化效果很差，且聚类效果不理想。

（4）对于高斯分布的数据，效果不如K-Means等传统聚类算法。

实战过程

数据准备

首先，需要准备一个数据集。本文以银行客户数据为例，根据客户的信息包括性别、年龄、信用分数、地理位置、是否有信用卡、账户余额等，将客户划分到不同的群组中。

部分数据样例 

DBSCAN模型

使用sklearn中的DBSCAN模型来实现DBSCAN聚类算法，需要调整两个参数：eps和min_samples。eps表示样本点的邻域半径，min_samples表示样本点在eps半径内的最小数量。代码如下：

# 定义 DBSCAN 模型，设置 eps 和 min_samples 参数
dbscan_model = DBSCAN(eps=0.6, min_samples=2)

# 对数据进行拟合
dbscan_model.fit(data)

聚类结果评估

聚类结果评估通常可以采用Silhouette score、Calinski-Harabasz score和Davies-Bouldin Index等指标来评估聚类效果。

# 输出 Silhouette score
print("Silhouette score:", silhouette_score(data, dbscan_model.labels_))

# 输出 Calinski-Harabasz score
print("Calinski-Harabasz score:", calinski_harabasz_score(data, dbscan_model.labels_))

# 输出 Davies-Bouldin Index
print("Davies-Bouldin Index:", davies_bouldin_score(data, dbscan_model.labels_))

可视化展示

使用t-SNE算法将数据降维到三维，并将DBSCAN聚类结果与降维后的数据合并。最终使用matplotlib绘制3D散点图，不同颜色的点表示不同的簇。

# 使用 PCA 进行降维和映射
# 使用 t-SNE 进行降维
tsne = TSNE(n_components=3, random_state=42)
reduced_data = tsne.fit_transform(data)
# 将 DBSCAN 结果与降维后的数据合并
clustered_data_df = pd.DataFrame(reduced_data, columns=['Dimension 1', 'Dimension 2', 'Dimension 3'])
clustered_data_df['Cluster'] = dbscan_model.labels_

from mpl_toolkits.mplot3d import Axes3D

# 创建三维坐标轴
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')

# 根据聚类标签绘制散点图
colors = ['red', 'green', 'blue', 'purple', 'orange', 'brown', 'pink', 'gray', 'olive']
for label in set(dbscan_model.labels_):
    if label == -1:
        cidx = -1
    else:
        cidx = label % len(colors)
    ax.scatter(clustered_data_df.loc[clustered_data_df['Cluster']==label, 'Dimension 1'],
               clustered_data_df.loc[clustered_data_df['Cluster']==label, 'Dimension 2'],
               clustered_data_df.loc[clustered_data_df['Cluster']==label, 'Dimension 3'],
               c=colors[cidx], marker='.', label='Cluster '+str(label))

# 添加坐标轴标签和图例
ax.set_xlabel('Dimension 1')
ax.set_ylabel('Dimension 2')
ax.set_zlabel('Dimension 3')
ax.set_title('DBSCAN Clustering (TSNE)')

plt.legend()
plt.show()

运行结果

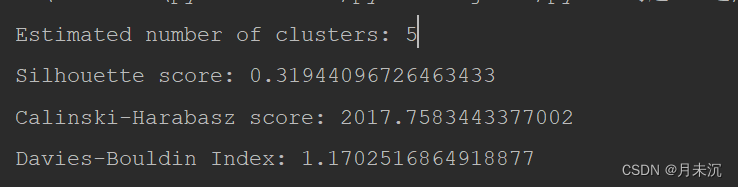
从 Silhouette score、Calinski-Harabasz score和Davies-Bouldin Index等指标，以及可视化图可以看出DBSCAN的聚类效果较好。

总结

本文介绍了如何使用Python实现DBSCAN聚类算法及其可视化展示。DBSCAN算法是一种基于密度的聚类算法，相对于传统的聚类算法具有更强的可扩展性和适应性。通过实现这个过程，读者可以更好地理解聚类算法的工作原理，为实际项目提供参考。

完整代码

# -*- coding = utf-8 -*-
# @Time : 2023/5/18 16:48
# @Author : xx
# @File : .py
# @Software: PyCharm

import pandas as pd
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn.manifold import TSNE
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt

df = pd.read_csv("select-data.csv")

data = []
for i in range(0, len(df["EstimatedSalary"])):
    mid = []
    mid.append(df["Geography"][i])
    mid.append(df["Gender"][i])
    mid.append(df["EB"][i])
    mid.append(df["Age"][i])
    mid.append(df["EstimatedSalary"][i])
    mid.append(df["NumOfProducts"][i])
    mid.append(df["CreditScore"][i])
    mid.append(df["Tenure"][i])
    mid.append(df["HasCrCard"][i])
    data.append(mid)
data = np.array(data)

# 定义 DBSCAN 模型，设置 eps 和 min_samples 参数
dbscan_model = DBSCAN(eps=0.6, min_samples=2)

# 对数据进行拟合
dbscan_model.fit(data)

# 输出模型估算的聚类数量
print("Estimated number of clusters:", len(set(dbscan_model.labels_)) - (1 if -1 in dbscan_model.labels_ else 0))
# 注意需要排除噪音点

# 输出 Silhouette score
print("Silhouette score:", silhouette_score(data, dbscan_model.labels_))

# 输出 Calinski-Harabasz score
print("Calinski-Harabasz score:", calinski_harabasz_score(data, dbscan_model.labels_))

# 输出 Davies-Bouldin Index
print("Davies-Bouldin Index:", davies_bouldin_score(data, dbscan_model.labels_))

# 使用 PCA 进行降维和映射
# 使用 t-SNE 进行降维
tsne = TSNE(n_components=3, random_state=42)
reduced_data = tsne.fit_transform(data)
# 将 DBSCAN 结果与降维后的数据合并
clustered_data_df = pd.DataFrame(reduced_data, columns=['Dimension 1', 'Dimension 2', 'Dimension 3'])
clustered_data_df['Cluster'] = dbscan_model.labels_

from mpl_toolkits.mplot3d import Axes3D

# 创建三维坐标轴
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')

# 根据聚类标签绘制散点图
colors = ['red', 'green', 'blue', 'purple', 'orange', 'brown', 'pink', 'gray', 'olive']
for label in set(dbscan_model.labels_):
    if label == -1:
        cidx = -1
    else:
        cidx = label % len(colors)
    ax.scatter(clustered_data_df.loc[clustered_data_df['Cluster']==label, 'Dimension 1'],
               clustered_data_df.loc[clustered_data_df['Cluster']==label, 'Dimension 2'],
               clustered_data_df.loc[clustered_data_df['Cluster']==label, 'Dimension 3'],
               c=colors[cidx], marker='.', label='Cluster '+str(label))

# 添加坐标轴标签和图例
ax.set_xlabel('Dimension 1')
ax.set_ylabel('Dimension 2')
ax.set_zlabel('Dimension 3')
ax.set_title('DBSCAN Clustering (TSNE)')

plt.legend()
plt.show()