【对称分量法应用】已知A、B、C三相电压或电流幅值和相位，求某一相的正序、负序、零序分量。

最新推荐文章于 2024-02-21 09:40:13 发布

张云闲

最新推荐文章于 2024-02-21 09:40:13 发布

阅读量2.9k

点赞数 13

文章标签：学习笔记

本文链接：https://blog.csdn.net/weixin_53070219/article/details/135086917

版权

前置条件：由电工基本原理可知，一组不对称的电气量可分解为正序、负序、零序三组电气分量，FA=FA1+FA2+FA0,FA1为正序分量，FA2为负序分量，FA0为零序分量，例：

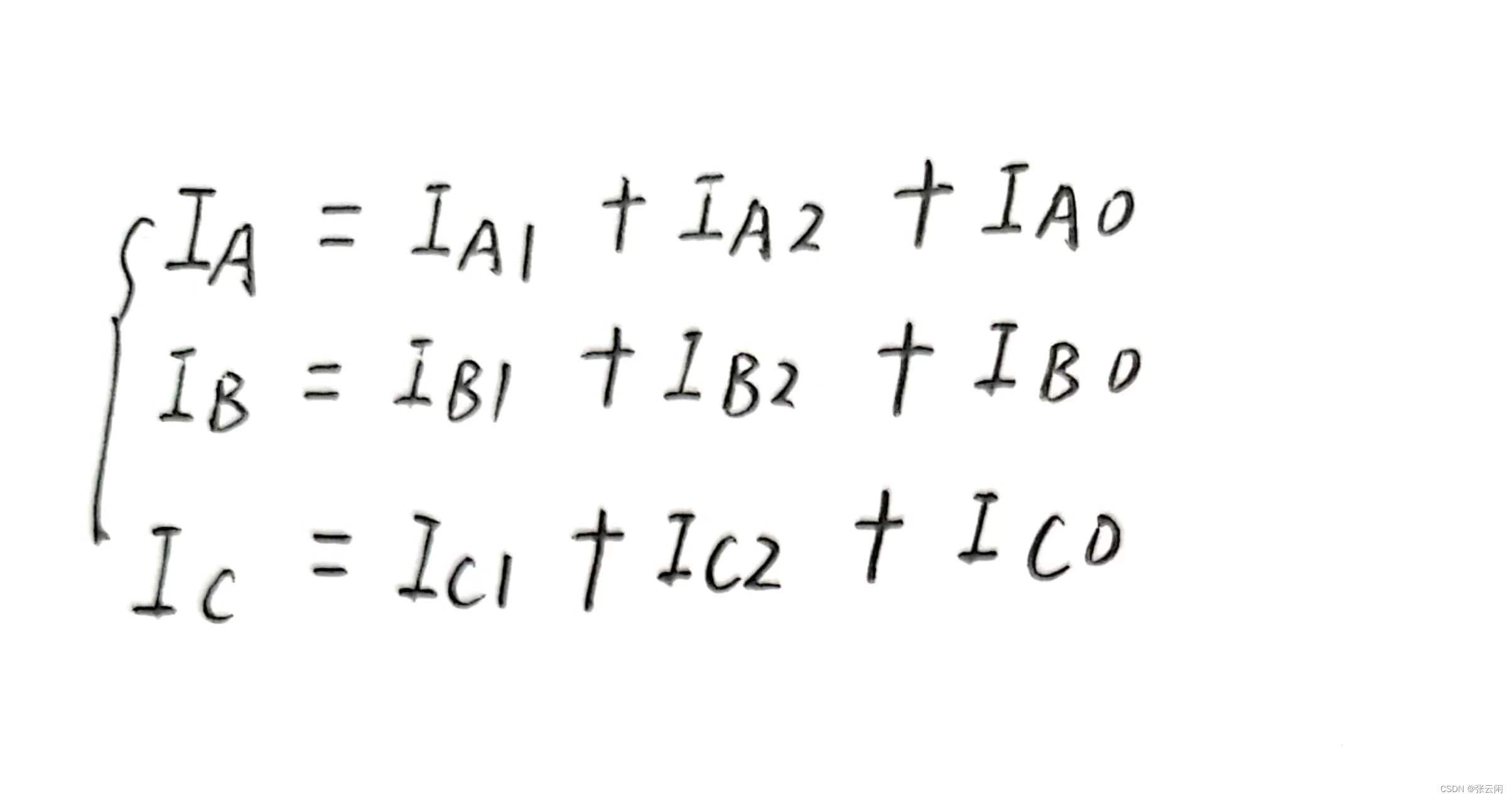
另外我们知道当A、B、C三相幅值相等，且按正序排列时，如下所示

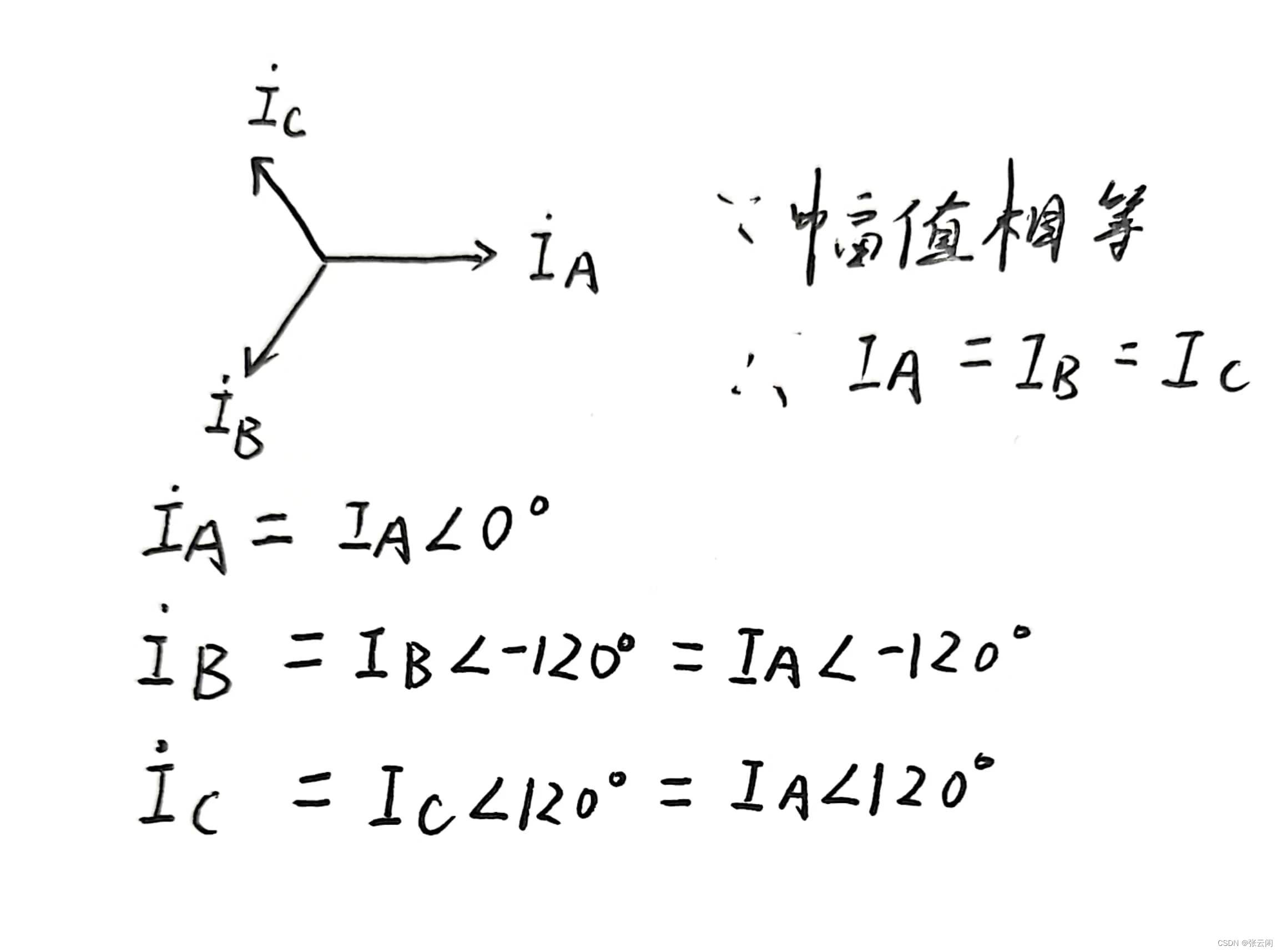
所以 $\dot{I_{B}}= \alpha ^{2}\dot{I_{A}}$ ， $\dot{I_{C}}= \alpha \dot{I_{A}}$ ， $\alpha$ 为单位相量算子， $\alpha = e^{^{j120^{\circ}}}$ 。

又 $\because$

$\therefore I_{A}=I_{A1}+I_{A2}+I_{A0}$

$\begin{matrix} \\ I_{B}=I_{B1}+I_{B2}+I_{B0}=\alpha^{2} I_{A1}+\alpha I_{A2}+I_{A0} \\ I_{C}=I_{C1}+I_{C2}+I_{C0}=\alpha I_{A1}+\alpha^{2} I_{A2}+I_{A0} \end{matrix}$

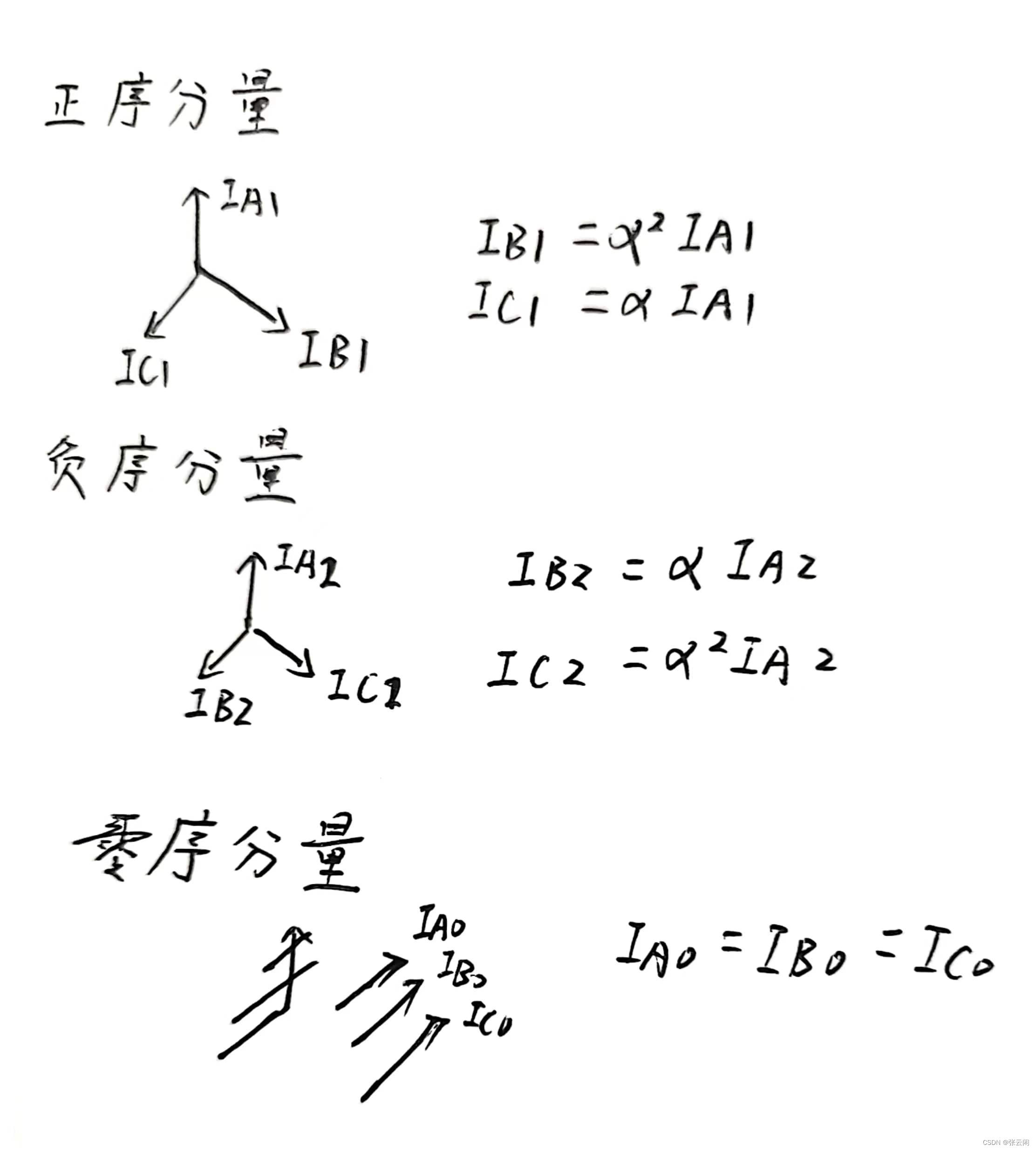
因此，当知道A、B、C三相的幅值和相位时，即可求得其各序分量。如下：

因此，我们可以推导出：

$\left\{\begin{matrix} \\ 3I_{A0}=I_{A}+I_{B}+I_{C} \\ 3I_{A1}=I_{A}+\alpha I_{B}+\alpha^{2} I_{C} \\ 3I_{A0}=I_{A}+\alpha^{2} I_{B}+\alpha I_{C}\end{matrix}\right.$

也就是各序分量的值，另外从中可以看出，当全量电流为零时，其中的分量并不为零。

并且可以从相量图的角度来理解，零序相量图中，三相相位相同，直接相加除以3即为A相零序分量；正序相量图中，B相滞后A相120°，C相超前A相120°，所以B相乘以 $\alpha$ ，C相乘以 $\alpha ^{2}$ ，与A相同相位后，除以3即为A相正序分量；负序相量图中，C相滞后A相120°，B相超前A相120°，所以C相乘以 $\alpha$ ，B相乘以 $\alpha ^{2}$ ，与A相同相位后，除以3即为A相负序分量。