本文介绍了高斯核函数的感性理解,以及从线性代数角度求解、推导高斯核函数、基函数的公式,并用pyhon实现了其函数以及图像绘制。
如何理解高斯核函数呢?我建议从用途入手。
作为机器学习中的一种算法,在解决分类问题中,高斯核函数便可发挥用途,当数据集不是线性可分的时候,需要利用核函数将数据集映射到高维空间,使其线性可分。
举个简单的例子:

在一维的线上,类似一条绳子上,有 红 红 蓝 蓝 红 红 串了六个小球,怎样才能用切一刀把原本的绳子切的只剩蓝色小球?
显然一刀是无法完成,我们需要用二维的思想来解决一维的问题,就需要把绳子映射到二维平面。此时再横着切一刀,就可以分类出蓝色小球。这就是高斯核函数解决问题的思想。

深入理解首先看定义
高斯核函数 (Gaussian kernel),也称 径向基 (RBF) 函数,是某种沿径向对称的标量函数,用于 将有限维数据映射到高维空间。形式如下:
 PRML教材公式(6.23)
PRML教材公式(6.23)
简而言之x’为核函数中心,||x-x'||为任意一点x到某一中心点x'之间的欧式距离(L2范数),我们选中一个中心点,假设蓝色小球之间的点,就会发现蓝色小球到中心的距离与红色小球到中心的距离是不同的,这可以在一定程度上解释径向基函数构建L2范数的原因。
上面的例子仅仅是一维到二维上的展示,那么样本的特征如果有n个,高斯核函数能不能解决呢?为了进行映射,我们要证明高斯核函数可以在无穷维度上应用:

如果样本点总共有P个,就要进行p次处理,如果x有m个特征,则Φ(x)基函数要展开到m维度。
各基函数形式为如下,参数为L2范数:

由于距离是径向同性的,因此称为径向基函数。由基函数表示的高斯核函数为:
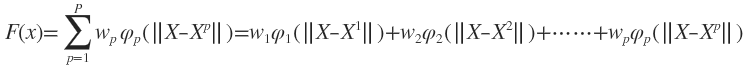
或者写成我们教材定义的形式
画图结果和代码如下:(下图分别为基函数和核函数)

基函数、核函数以及画图的python代码如下
from re import X
import matplotlib.pyplot as plt
import numpy as np
import numpy.linalg as la
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return (n*factorial(n-1))
def gaussiankernel(sigma,x,x0):
y=[]
for i in x:
y0=np.exp(-(la.norm(i-x0)**2) / (2 * sigma ** 2))
y.append(y0)
return y
def gaussianji(sigma,x,n,x_di):
y=[]
for i in range(0,n):
x_new=(x-x_di[i])
y0=(np.exp(-(x_new**2)))#*((x_new/sigma)**i)*np.sqrt((2**i)/factorial(i))
y.append(y0)
y=np.array(y)
return y
N=11
x_di=np.linspace(-1,1,N)
x=np.linspace(-1,1,N)
j=-10
color=['red', 'black', 'blue', 'brown', 'green','red', 'black', 'blue', 'brown', 'green','red', 'black', 'blue', 'brown', 'green']
plt.subplot(2,3,2)
for k in x:
y=gaussianji(1,k,N,x_di)
plt.plot(x_di,y,linewidth=0.5,color=color[abs(j)])
j=j+1
plt.subplot(2,3,5)
y=gaussiankernel(1,x,0)
plt.plot(x,y,linewidth=0.5,color='blue')
plt.show()























 2506
2506

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










