锁相环（PLL）的原理

1.何为锁相环

       锁相环在工作过程中，当输出信号的频率与输入信号的频率相等时，输出电压与输入电压保持固定的相位差值，即输出电压与输入电压相位被锁定，此即为锁相环名称的由来。

       锁相环是一个相位误差的控制系统，通过比较参考信号和输出信号之间的相位，产生相位误差来调整输出信号，达到与参考信号同频的目的。锁相环系统框图如下所示。

2.硬件锁相环 

       硬件锁相环主要由鉴相器(PD-Phase Detector)、环路滤波器(LF-Loop Filter)和压控振荡器(VCO-Voltage Controlled Oscillator)这三部分组成。

2.1鉴相器(PD-Phase Detector)

       鉴相器通过比较输入信号和压控振荡器输出信号的相位，输出一个关于该信号相位差的函数。

2.2环路滤波器(LF-Loop Filter)

       环路滤波器可以理解成一个低通滤波器，滤除鉴相器输出电压中的高频分量和噪声，只保留低频分量。

2.3压控振荡器(VCO-Voltage Controlled Oscillator)

       压控振荡器受环路滤波器输出电压控制，压控振荡器的振荡频率向输出信号的频率靠拢，直到两者频率相等。同时使压控振荡器的输出信号和输入信号之间的相位保持特定的关系，用以锁相。

2.4锁相环各部分基本原理

2.4.1鉴相器(PD-Phase Detector)原理分析

       鉴相器的形式多种多样，目前常用的是正弦波鉴相器，用乘法器实现。假设鉴相器的输入信号为：

       压控振荡器的输出信号为：

       一般情况下，ωi和ωo不相等，为了便于比较两者之间的相位差，将两者统一为ωo作为参考。因此，输入信号的形式变换为： 

 其中表示输出信号角频率与输入信号角频率的差，属于固有的频率差。

        为简化分析，相位q统一用φ表示，因此改写之后的压控振荡器输出信号为：

       此时，经过变换之后的鉴相器输入信号和压控振荡器的输出信号分别为：

其中，

       由前述分析可知，鉴相器常用理想的模拟乘法器来实现。因此将鉴相器输入信号和压控振荡器的输出信号相乘得到：

其中Am为乘法器的增益。

       利用如下所示的积化和差公式：

       因此乘积结果化为：

 2.4.2环路滤波器(LF-Loop Filter)原理分析

 环路滤波器是线性电路，主要由电阻、电容和电感元件组成，有时还包含运算放大器。由鉴相器部分所述，它是一个低通滤波器，主要用于滤除鉴相器输出的高频分量。PLL中常用的环路滤波器有:

（1）RC积分滤波器：

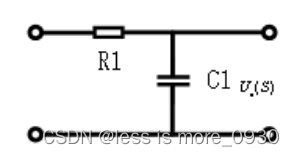
（2）无源比例积分滤波器：

（3）有源比例积分滤波器：

       无源比例积分滤波器和有源比例积分滤波器对电压进行积分，可以生成很大的VCO控制电压。

       由鉴相器乘积输出结果可知，前半部分为高频分量，后半部分为低频分量。因此需要通过环路滤波器（线性电路，主要由电阻、电容和电感元件组成，有时还包含运算放大器。常用的环路滤波器：RC积分滤波器、无源比例积分滤波器、有源比例积分滤波器）将高频分量滤除，输出低频分量，环路滤波器传递函数为：

其中Klpf是滤波器的增益，Tlpf是滤波器的时间常数。 

       滤除高频成分后，环路滤波器输出信号为：

式中，为常数，φ(t)=φi(t)-φo(t)。由该式子能清楚的了解鉴相器和环路滤波器的作用，本质上是将两个信号的相位差φ(t)转化成电压Ud(t)输出。 

       由极限的知识可知：

       因为φ(t)=φi(t)-φo(t)很小，考虑当φ(t)=φi(t)-φo(t)≤30°时，令：

       因此环路滤波器的输出变为：

       因此，当φ(t)=φi(t)-φo(t)≤30°时，鉴相器的输入和环路滤波器的输出可以看成是线性关系，输出电压与相位差成正比。

       

2.4.3压控振荡器(VCO-Voltage Controlled Oscillator)基本原理分析

       压控振荡器能够根据环路滤波器输出电压的控制，将振荡器的频率向输入信号的频率靠拢，直到两者的频率相同，使得VCO的输出信号和输入信号的相位保持一定，从而达到相位锁定。它本质上就是一种电压-频率变换器。在实际电路中，压控元件一般由变容二极管构成，环路滤波器输出的电压加到压控振荡器回路上的变容二极管上，使得变容二极管的结电容发生改变，从而使振荡器的频率发生改变。

       用压控振荡器输出信号的瞬时振荡频率ωo(t)与环路滤波器的输出电压Uc(t)之间的关系表示压控振荡器的调频特性，如下图所示。

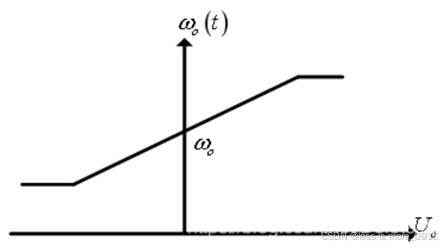
       上图表明在特定范围内，ωo(t)和Uc(t)成正比，因此可以写ωo(t)关于Uc(t)的一次函数为：

其中，ωo表示VCO的中心频率。

       在锁相环中，我们需要的是相位的变化，根据相位是频率的积分关系，可以将上式ωo(t)输出变换为瞬时相位φ1(t)，即：

        由环路滤波器输出电压引起的相位变化量为： 

2.5状态空间方程

       定义状态向量为：

       根据相位误差和滤波器输出电压的动态关系，可以写出状态方程：

       输出方程输出信号为相位误差：

2.6总结

       基本原理：当没有输入信号时，VCO以自由频率ωo振荡。如果环路有了一个输入信号Ui(t)，开始时，输入频率总是不等于自由振荡频率，即ωi≠ωo。若两者频率相差不大，在适当范围内鉴相器输出误差电压，经过环路滤波器变换后控制VCO的频率，使得输出频率变化到接近ωi，且环路输入输出信号相位误差为固定值φ。

3.软件锁相环

3.1基于同步旋转坐标系的锁相环

       基于同步旋转坐标系的锁相环等效原理图如下图所示。

       对称三相电压表达式为：

其中，θ=ωt，ω为电网同步角频率。

       Clark变换（abc→αβ）：

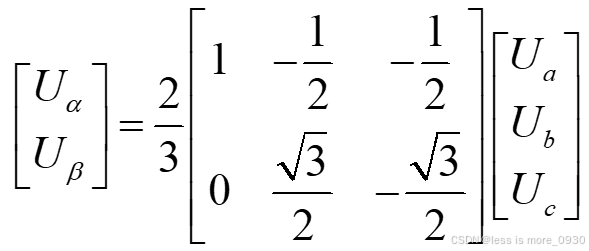
       Park变换（αβ→dq）：

       所以等幅值3r/2s变换矩阵为：

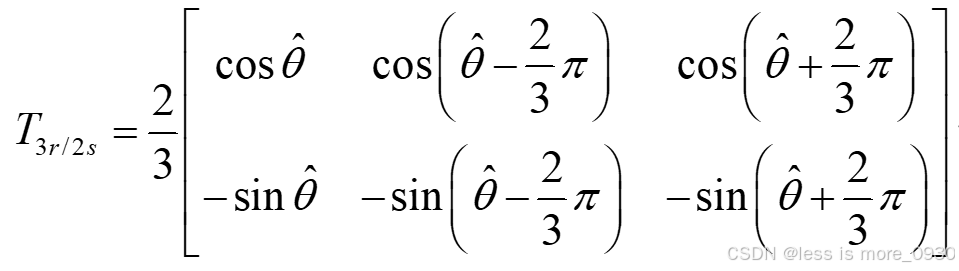
推导过程为：

其中，θ为三相电压合成矢量与α轴之间的夹角，θ-hat（θ¢）是d轴与α轴之间的夹角即PLL输出的相角，趋近于θ，但两者不相等。

       因此，可得q轴的电压分量为：

推导过程为：

       当角度θ足够小时，sinθ≈θ，因此有（非线性化的原因）：

       闭环传递函数为：

       当dq坐标系与三相电压合成矢量Uδ旋转角速度相同时，Ud、Uq幅值恒定，表现为直流量。设置初始条件Uq=0，通过PI调节器将Uq=控制到零，即Uδ与d轴重合，则此时d轴和α轴的夹角即为Uδ的相位，锁相环的角频率即为系统频率ωc。

3.2软件锁相环仿真分析

       仿真电路如下图所示：

其中，激励具体实现为：

其中，基于同步旋转坐标系的锁相环具体实现为：

（1）当三相电压对称时。

       由Clark变换可知，Va和Vb的初值分别为0和−2202-220√2。初始时锁相环输出的相角为0，且此时三相电压初相位也为0，故Vq的初始幅值为-2202 ，√2  ，输出频率为负的最大值。因此在仿真初始阶段频率为负，相角先减后增。

（2）当三相电压对称，但相位跳变时。

       当A相和B相相位跳变时，Ud和Uq在相位跳变的瞬间存在一个尖峰，相位跳变完成后，重新达到稳态。

（3）当三相电压对称，但电压跌落时。

       在0.1s三相电压跳变成完全一致，由Ud和Uq的表达式可知，此时Ud和Uq均为0，由锁相环原理可知， 锁相环仍能锁出相位和频率。

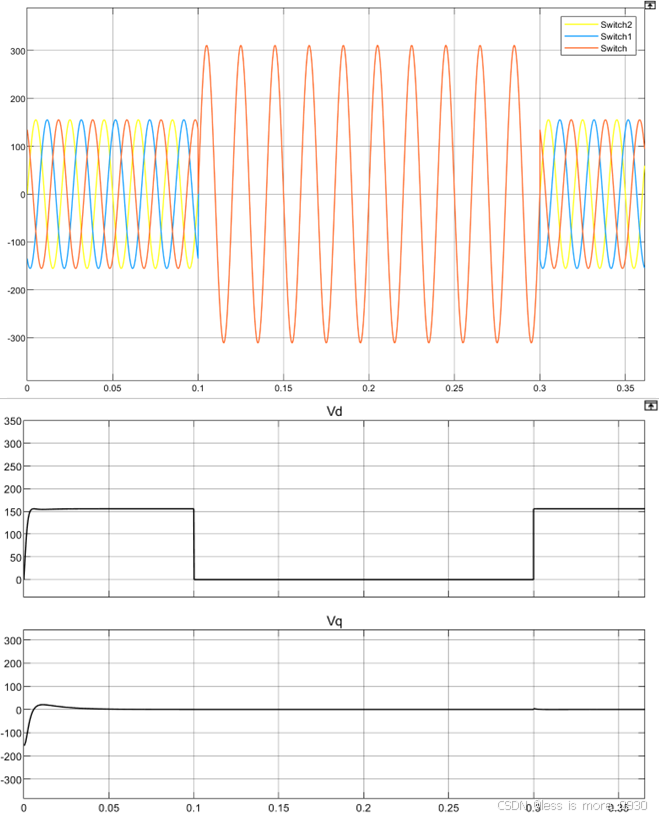
（4）三相电压对称+正序扰动。

       A相存在频率为120Hz的正序扰动，由Ud和Uq的表达式可知在稳态下，均由稳态值和一个正（余）弦分量组成，因此Ud、Uq和f均存在脉动，ωt存在畸变。

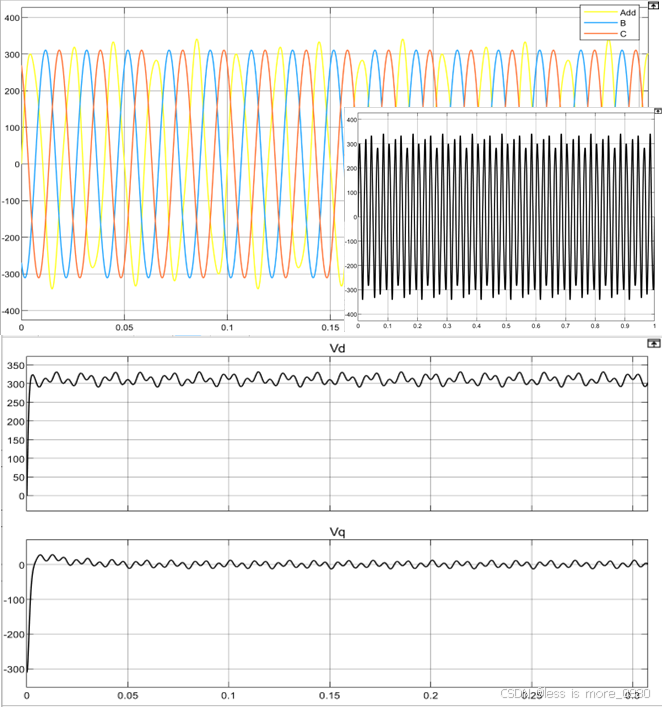
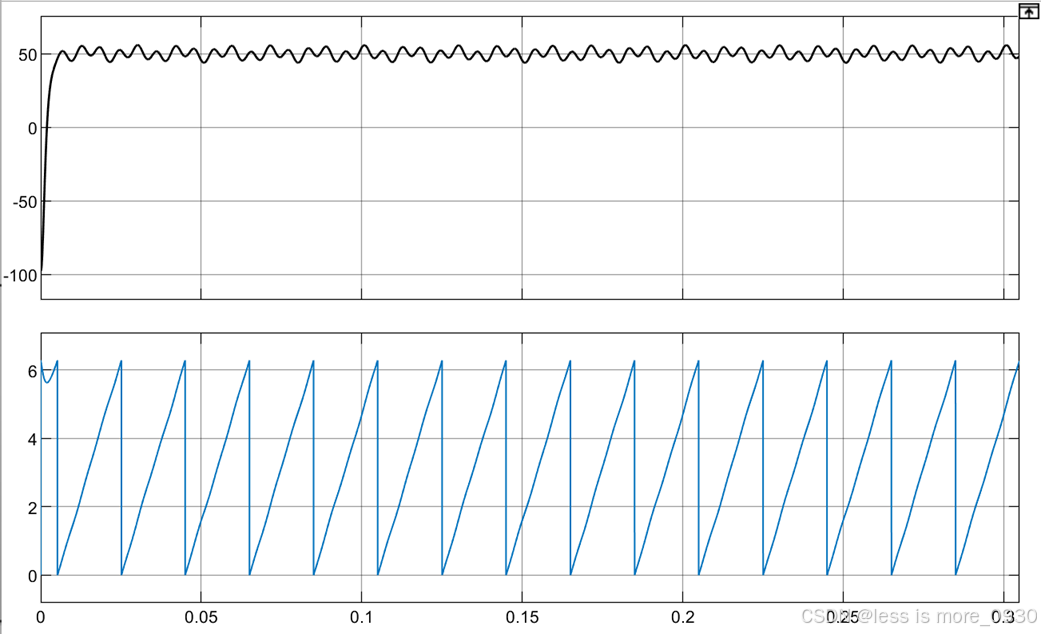
（5）电压跌落造成三相不对称。

       由Ud和Uq的表达式可知，当三相电压不对称时，Ud和Uq由一个恒定量和一个余弦分量组成，因此Ud、Uq和f均存在脉动，ωt存在畸变。

参考文献

[1]Dai Z, Li G, Fan M, et al. Global stability analysis for synchronous reference frame phase-locked loops[J]. IEEE Transactions on Industrial Electronics, 2021, 69(10): 10182-10191.