风力发电机输出功率模型

less is more_0930

于 2024-12-23 15:10:26 发布

阅读量1.9k

点赞数 33

分类专栏：《新型电力系统》文章标签：学习笔记

本文链接：https://blog.csdn.net/weixin_53126442/article/details/144667189

版权

《新型电力系统》专栏收录该内容

11 篇文章

订阅专栏

风力发电机输出功率模型主要包括风力发电机基本功率方程模型和风力发电机功率曲线模型。选择合适的风力发电机输出功率模型对发电系统的设计至关重要。

1.双馈异步风力发电系统原理

图3为基于双馈发电机的变速风力发电系统示意图。

双馈风力发电机的定子绕组直接与电网相连，转子绕组通过变频器与电网连接，转子绕组电源的频率、幅值和相位按运行要求由变频器自动调节，机组可以在不同的转速下实现恒频发电，满足用电负载和并网的要求。在双馈异步风力发电机中，转子和定子都参与励磁，并且都可以与电网进行能量的交换。

转子绕组相对于定子磁场的机械旋转频率，可以通过转速换算得到：

式中，fm为转子机械旋转频率；np为DFIG极对数；nr为转子机械转速。

电机运行的核心是，转子磁场的旋转频率相对于定子磁场必须保持为同步频率fs，即两者之间的相对运动必须同步。

转差率s是衡量转子速度不足的量，反映了转子转速与同步转速的偏差，定义为：

式中，s为转差率；ns为同步转速；ne为转子电气转速。

不考虑转差率时，转子的机械角速度ωm和电气角速度ωe满足下式：

式中，ωe为不考虑转差率时的转子电气角速度；np为DFIG极对数；ωm为转子机械角速度。

考虑转差率时，转子的机械角速度ωm和电气角速度ω¢e满足下式：

式中，ωe为不考虑转差率时的转子电气角速度；ω¢e为考虑转差率时的转子电气角速度；np为DFIG极对数；ωm为转子机械角速度。

在额定负载下运转的异步电动机，其转差率一般为0.01~0.06，因此在额定负载下分析时，可近似认为转子的机械角速度ωm和电气角速度ωe满足不考虑转差率时的关系式。

磁场旋转速度：为了使定子产生的电流保持电网频率，转子的磁场必须相对于定子以同步速度旋转。假设同步转速是1500 RPM，而当前转子转速是1200 RPM，那么转子磁场需要以300 RPM的相对速度旋转，这样在定子看来，总的磁场旋转速度仍然是1500 RPM。

当发电机转速低于同步转速时，转子励磁电流产生的旋转磁场与转子转速方向相同，此时需要增加转子励磁电流的频率来补偿转速的不足，以保持定子输出电能的频率恒定。
当发电机转速高于同步转速时，转子励磁电流产生的旋转磁场与转子转速方向相反，此时需要降低转子励磁电流的频率来保持定子输出电能的频率恒定。
当发电机的转速等于气隙旋转磁场的转速时，发电机处于同步速运行，变频器应向转子提供直流励磁，此时，转子的制动转矩与转子的机械转速方向相反，与转子感生电流产生的转矩方向相同，定子和转子都向电网馈送电功率。

定子磁场转速就等于转子电气转速与转子励磁磁场转速之和，用数学表达式表示即为：

式中，ns为同步转速；nr为转子励磁磁场转速；ne为转子电气转速。

用机械转速来表达为：

式中，ns为同步转速；nr为转子励磁磁场转速；np为DFIG极对数；nm为转子机械转速。

用频率的形式来表示为：

式中，fs为定子频率，也为电网频率；fr为转子电流频率；np为DFIG极对数；fm为转子机械旋转频率。

2.双馈异步风力发电系统基本功率传递关系

动能定理：

式中，Ek是物体的动能，m是物体的质量，v是物体的速度。

在流体力学中，如果要计算某一瞬间、某一截面上气流的动能，可以将其视为一个连续流体微元（或称为流体质点）的集合，每个微元都具有一定的质量和速度。对于每个微元，其动能可以表示为：

式中，Ek是气流微元流体的动能，m是微元的质量，v是微元的速度。

在流体力学中，我们更常用的是体积流量（Q）和质量流量（）来描述气流的流动状态。体积流量是单位时间内通过某一截面的气体体积，而质量流量则是单位时间内通过某一截面的气体质量，两者的关系可以通过气体密度（ρ）来表示：

式中，为质量流量，ρ为气体密度，Q为体积流量。

体积流量（Q）的表达式为：

Q=Av

式中，Q为体积流量，A为流体通过的横截面面积，v为流体通过截面时垂直平均速度。

因此，联立上三式可得，一个体积为Q，密度为ρ、速度为v的流体的动能为：

式中，Ek是流体动能，ρ为气体密度，A为流体通过的横截面面积，v为流体通过截面时垂直平均速度。

风力发电机的基本功率方程依据风能功率方程（理论可获得的最大风能，在单位时间内流过垂直于风速截面积A的风能即风功率。）：

式中，ρa为空气的质量密度；V为垂直风速；A为风力发电机风轮扫过的面积。

由圆的面积可得，风力发电机风轮扫过的面积为：

式中，D为风轮直径。

风力发电机安装地的空气密度是影响风力发电机输出功率的一个重要因素，一般与当地的大气压力、环境温度和海拔高度等因素有关，其基本方程为：

式中，p为大气压力；T为环境温度；h为海拔高度；Rc为摩尔气体常量，287.05 J/(K·mol)；g为重力加速度。

在计算风功率时，选取的风速与高度有关。有许多复杂的公式被用来体现风速随高度的变化，但过于复杂，对一般的工程研究没有任何用处。许多研究人员致力于寻找更简单的表达式，即使它们在理论上可能不精确，也会产生令人满意的结果。这些简单的表达式中最常见的是幂律，表示为：

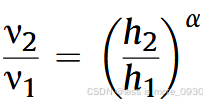
式中，v2为换算得到的轮毂高度处的风速；v1为风速计高度测得的风速；h2为轮毂所处的高度；h1为风速计所处的高度。

从上式中能发现，风速，即风机产生的输出能量，取决于风机所处的高度和地形的粗糙度。轮毂高度和地形粗糙度（以地面摩擦系数a衡量）的影响如图4所示。从图4可以看出，轮毂高度和地面摩擦系数对风速的影响较大。因此，为了计算风力机的性能，必须将风速计高度测得的风速按上式换算为轮毂高度处的风速。

风能转换系统（WECS）的基本功率级如图5所示。

在垂直于风速为v（m/s）、空气密度为ρ的气流的横截面积A内可用的瞬时风力表示为：

式中，Pw为风功率；ρ为空气密度；A为横截面积；v为截面上的垂直风速。

该风功率通过风力机转化为机械功率Pm：

式中，Pm为风功率转化而来的机械功率；Cp为风能利用系数；Pw为风功率。

然后将这种机械动力提供给机械传动系统（齿轮等），机械传动系统的输出，即Pt作为输入馈送给发电机：

式中，Pt为机械传动系统的输出功率；hm为机械传动系统的传输效率；Pm为风功率转化而来的机械功率。

然后得到发电机的输出功率为：

式中，Pe为风力发电机输出的电功率；hg为风力发电机的发电效率；Pt为机械传动系统的输出功率。

综上所示，双馈异步风力发电机的输出功率为：

3.基本功率方程模型

由上一节的风力发电机的基本功率传递关系，以及各参数的表达式可得：

式中，Po为风力发电机输出的电功率；Pw为风功率；Cp为风能利用系数；ht为机械传动系统的传输效率；hg为风力发电机的发电效率；ρa为空气密度；A为横截面积；V为截面上的垂直风速；P为大气压力；T为环境温度；h为海拔高度；Rc为摩尔气体常量，287.05 J/(K·mol)；g为重力加速度；D为风轮直径。