博客:Alex Chin, & Tony Qin. (2023.02.25). Quantifying Efficiency in Ridesharing Marketplaces. Link: https://eng.lyft.com/quantifying-efficiency-in-ridesharing-marketplaces-affd53043db2
论文:Chin, Alex, and Zhiwei Qin. “A Unified Representation Framework for Rideshare Marketplace Equilibrium and Efficiency.” SIGSPATIAL 2023 (2023).
推文作者:郭王懿,陈泰劼,张云天
编者按:
共乘出行极大地改变了人们的日常出行方式。如何高效运营背后的双边平台是极具挑战性的工作。滴滴出行、Lyft公司是其中的佼佼者。本专题将探讨双边平台运营中的一个关键问题:如何科学度量双边平台的运营效率?
本专题分为上下两篇,递进推出。其中,上篇围绕滴滴出行、上海财经大学发表在统计学“四大”期刊之一《Journal of the American Statistical Association》的一篇文章 [1] 展开(https://mp.weixin.qq.com/s/kfMGWrqXwEmhzOLuG9nxVw);下篇关注解读Lyft公司的一篇优质技术博客 [2] 和SIGSPATIAL 2023录用的一篇论文 [3](https://sigspatial2023.sigspatial.org/)。
[1] Zhou, F., Luo, S., Qie, X., Ye, J., & Zhu, H. (2021). Graph-based equilibrium metrics for dynamic supply–demand systems with applications to ride-sourcing platforms. Journal of the American Statistical Association, 116(536), 1688-1699.
[2] Alex Chin, & Tony Qin. (2023.02.25). Quantifying Efficiency in Ridesharing Marketplaces. Link: https://eng.lyft.com/quantifying-efficiency-in-ridesharing-marketplaces-affd53043db2
[3] Chin, Alex, and Zhiwei Qin. “A Unified Representation Framework for Rideshare Marketplace Equilibrium and Efficiency.” SIGSPATIAL 2023 (2023).
引言
通常共乘出行的供需市场健康取决于乘客和司机的时空分布,但是在时空分布较为复杂的双边平台中,我们很难定义“市场效率”和“供需平衡”。比如,“我们有足够的司机吗?”可以有很多种理解方式:
- 在当前地点下是否有足够的司机来保证服务质量?
- 在整个系统中是否有足够的司机可以满足任意地点的乘客订单?
- 是否有足够的收入来维持司机的收益率?
为了更好的描述市场状态,我们必须研究监测市场状态的指标或方法。本文主要关注以下三个主要的问题:
- 指标过多难以选择:现有的市场运行指标非常繁多,有乘客方面的指标包括取消率、预计到达时间、履约率等,司机方面的指标有司机在线时长,司机服务率(时间利用率)和收入等,平台方面的指标有乘车数量、财务指标等。同时监控大量指标是非常困难的,很难找到侧重点;并且这些指标通常容易受到外部变化(交通、天气、机场延误)的冲击影响。
- 缺乏决策输出:指标的变化无法指导下一步的最佳决策,平台有很多工具可以改善市场状况,包括定价、调度、激励政策等,但是需要决策如何进行市场调整。
- 指标信息冗杂:包含大量噪音的指标表示的信息通常非常复杂, 分析师很难从指标中掌握核心发生的事情。此外这些指标的单位通常异构,因此协调不同指标的方法并不直观。
目前共乘出行双边市场迫切需要一个供需状态的简洁表示方法,同时需要一个共乘出行市场效率的表征方法和数值测试。本文提出了一个基于GEM的供需时空状态度量方法和双边市场效率评估统一框架。
一、基于图结构的均衡度量方法(GEM)回顾
我们在 共乘出行(上)中详细介绍了GEM框架。
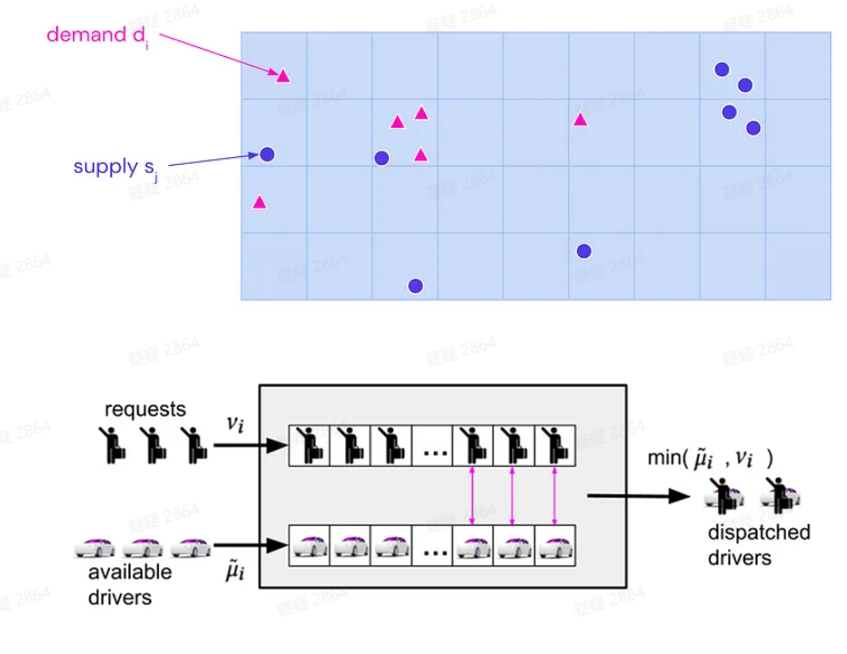
这里我们同样将城市划分为 N N N个区域,构建图 G = ( V , E ) G =(\mathbb{V},\mathbb{E}) G=(V,E),其中 v ∈ V v\in\mathbb{V} v∈V分别代表 N N N个节点, ∣ V ∣ = N |\mathbb{V}|=N ∣V∣=N,每个边$e_{ij}=(vi, vj)∈ \mathbb{E} 都有一个对应的运输成本 都有一个对应的运输成本 都有一个对应的运输成本w_{ij} ,代表从 ,代表从 ,代表从i 区域转移到 区域转移到 区域转移到j 区域需要的成本。从图 区域需要的成本。从图 区域需要的成本。从图G 和权重矩阵 和权重矩阵 和权重矩阵W=(w_{ij}) 可以定义两种额外的属性:邻居节点 可以定义两种额外的属性:邻居节点 可以定义两种额外的属性:邻居节点N_i 和成本矩阵 和成本矩阵 和成本矩阵C =(c_{ij}) 。邻居节点 。邻居节点 。邻居节点N_i 是与节点 是与节点 是与节点i 直接相连的节点集合,成本矩阵定义为 直接相连的节点集合,成本矩阵定义为 直接相连的节点集合,成本矩阵定义为c_{i j}=\inf_{\text {paths } p} \sum_{(k, \ell) \in p} w_{k \ell} ,用于描述节点之间的最小转移成本。每个节点都有对应的供应和需求数目分别用测度 ,用于描述节点之间的最小转移成本。每个节点都有对应的供应和需求数目分别用测度 ,用于描述节点之间的最小转移成本。每个节点都有对应的供应和需求数目分别用测度\mu 和测度 和测度 和测度\nu 表示,比如 表示,比如 表示,比如\mu_i 就表示节点 就表示节点 就表示节点i 中可供调度的司机的数量, 中可供调度的司机的数量, 中可供调度的司机的数量,\nu_i 就表示节点 就表示节点 就表示节点i$中呼叫司机的乘客的数量。
1. GEM优化问题
根据上述定义,下面回顾一下GEM优化问题,GEM定义的优化问题由供需不匹配程度和转移成本两部分构成,同时需要满足供需平衡的调度约束:
ρ λ ( μ , v ) = min γ ∈ Γ { ∥ v − μ ~ ∥ 1 + λ ∑ v i ∈ V ∑ v j ∈ V c i j γ i j } s . t . ∑ v j ∈ N i γ i j = μ i , ∑ v j ∉ N i γ i j = 0 , μ ~ i = ∑ v i ∈ N j γ j i , for all v i ∈ V . \begin{gathered} \rho_\lambda(\mu, v)=\min _{\gamma \in \Gamma}\left\{\|v-\tilde{\mu}\|_1+\lambda \sum_{v_i \in \mathcal{V}} \sum_{v_j \in \mathcal{V}} c_{i j} \gamma_{i j}\right\} \\ s.t.\sum_{v_j \in \mathcal{N}_i} \gamma_{i j}=\mu_i, \quad \sum_{v_j \notin \mathcal{N}_i} \gamma_{i j}=0, \quad \tilde{\mu}_i=\sum_{v_i \in \mathcal{N}_j} \gamma_{j i}, \quad \text { for all } v_i \in \mathcal{V} . \end{gathered} ρλ(μ,v)=γ∈Γmin⎩
⎨
⎧∥v−μ~∥1+λvi∈V∑vj∈V∑cijγij⎭
⎬
⎫s.t.vj∈Ni∑γij=μi,








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








