机器学习（五）SVM--机器学习中最美推导

支撑向量机建模

问题描述

给定训练数据集训练数据集：训练数据集： D = { x i , y i } i=1...n ； y i ∈ { − 1 , 1 } ( { 0 , 1 } ) D=\overset{\text{}}{% \left\{x_i,y_i \right\}% }% \underset{\text{i=1...n}}{}；y_i\in \{-1,1\}(\{0,1\})% D={xi​,yi​}​i=1...n​；yi​∈{−1,1}({0,1})
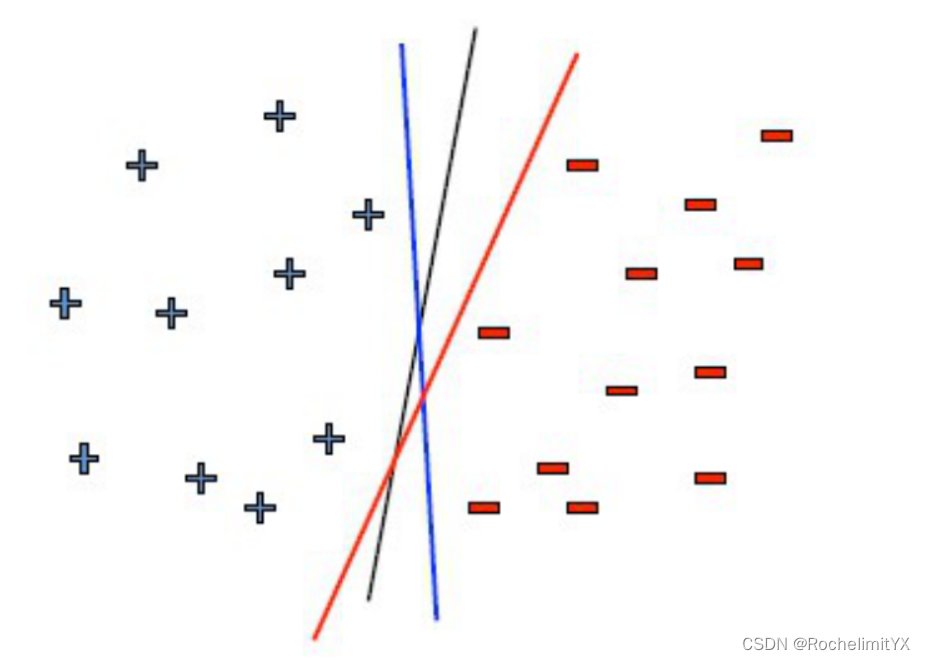分类器学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面将不同类别的样本分开，但是，如上图所示，能够将训练样本分开的划分超平面可能有很多，哪个分类器更好呢？
朴素自然的，直观上我们会选择位于两类训练样本正中间的划分你超平面，也就是具有最大分隔区间的，这样可以保证分类精度相同时，推广能力更佳，潜在认为当我有一个新的数据时分类器也能把它分好，即使数据有一定的噪声，这根线分的也是最稳定的；总的来说，就是我们要找能完美把数据分开，且往两边拉开间隔最大的超平面，以保证对未来数据泛化能力最强

Large Margin

学习机：$f_w(x)=w^{T}x+b$

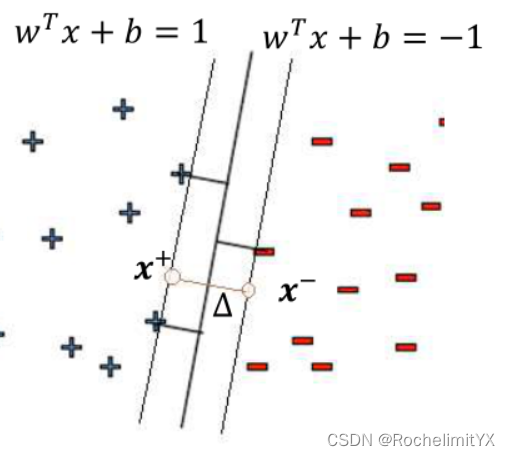
假设间隔最大的那个分类面往两边拉开得到的直线是$w^{T}x+b=1$和$w^T+b=-1$；也可以设为$w^{T}x+b=c$和$w^T+b=-c$，两边同时除以c，把制度变换放在w和b中，反正这两是变量；接下来，我们就开始找寻符合两个要求的超平面
首先，如何刻画每个样本都分对了？
对于每一个$x_i$,$y_i$都分对了，则有$f_w(x_i)y_i\ge 0$,这是我们在感知机模型里提到的线性可分假设；那么在上述的假设下，对于每个样本，分对了，有：
$$(w^T{x}_i+b)y_i\ge 1$$
因为
$$\{\begin{array}{ll}\text{当该样本是正类时}{y}_i=1& w^{T}x+b\ge 1\\ \text{当该样本是负类时}{y}_i=-1& w^{T}x+b\ge -1\end{array}$$，将二者相乘，无论正负样本都有$(w^T{x}_i+b)y_i\ge 1$；
第二，如何表示Margin？
如图所示，我们假设$x^{+}$位于直线$w^{T}x+b=1$上，$x^{-}$位于直线$w^{T}x+b=-1$上，这是肯定的，如果正样本还在这条线的左边或者负样本还在这条线的右边，我们将$w^{T}x+b=1$往左边拉，或者将$w^{T}x+b=-1$往右边拉，直到碰到相应的边界点为止，其实这两个点就是我们所说的支撑向量的一种，支撑向量机有了这些支撑向量的样本，其它的样本有没有都无所谓了
$$△=||x^{+}-x^{-}||=？$$
等式右边$$w^{T}x+b-(w^T{x}^{-}+b)=w^T(x^{+}-x^{-})=1-(-1)=2$$$x^{+}$位于直线$w^{T}x+b=1$上，$x^{-}$位于直线$w^{T}x+b=-1$上
又有$w^T$代表了$w^x+b=c$的垂线，显然是和直线$x^{+}-x^{-}$平行的，所以有
$$||w^T(x^{+}-x^{-})||=||w^T||.||(x^{+}-x^{-})||cos0=||w^T||.||(x^{+}-x^{-})||=2$$
$$△=||x^{+}-x^{-}||=\frac{2}{||w^T|{|}_2}=\frac{2}{||w|{|}_2}$$

接下来我们就是要在样本分类准确的前提下最大化Margin
我们试图把样本在严格分类准确的前提下最大化Margin；Margin内在含义：分类面能把间隔拉开
即$$$\max \frac{2}{||w||}$$
为了好算，等价于$$\underset{w,b}{\min }\frac{1}{2}{w}^{T}w$$
$$s.t.(w^T{x}_j+b)y_j\ge 1,forallj=\mathrm{1...}n$$
现在问题就转化为了上述的QP问题<–显然目标函数对于w而言是凸函数，约束对w和b是线性的

当数据非线性可分怎么玩

以上SVM算法是基于线性可分假设的，当有一些错落的电视整个算法将崩溃，因为正类里面混有负类，负类里面混有正类，导致可行域是空集，故而我们找不到一个线性分类面把所有的数据分开
对于有些样本分不开的情况，如何让它继续可行？
加入松弛，允许分类误差；
则上述问题可描述为
$$\underset{w,b,{\xi }_j}{\min }\frac{1}{2}{w}^{T}w+C\sum _j{\xi }_j$$
$$s.t.(w^T{x}_j+b)y_j\ge 1-{\xi }_j,forallj=\mathrm{1...}n$$
$${\xi }_j\ge 0,forallj=\mathrm{1...}n$$
其中${\xi }_j$为松弛变量，C为惩罚因子,可见，如此描述的问题仍为QP问题，因为对于增加的${\xi }_j$，增加的是${\xi }_j$线性的目标函数，线性的约束，仍然可以保证全局极优，同时要注意，尽管我们允许了松弛，但是也要让我的松弛尽可能的小；在我们的可行域中，为了让分不开的数据尽量影响小，否则的话，${\xi }_j$都会走向正无穷，显然失去了意义

优化策略–对偶优化

对于上述两个QP问题，我们如何求解呢？
当然我们可以直接调用现成的QP工具包求解，但是采用对偶优化，能让我们清晰地看到SVM深刻地机器学习方法的内涵
（1）$$\underset{w,b}{\min }\frac{1}{2}{w}^{T}w$$
$$s.t.(w^T{x}_j+b)y_j\ge 1,forallj=\mathrm{1...}n$$
（2）$$\underset{w,b,{\xi }_j}{\min }\frac{1}{2}{w}^{T}w+C\sum _j{\xi }_j$$
$$s.t.(w^T{x}_j+b)y_j\ge 1-{\xi }_j,forallj=\mathrm{1...}n$$
$${\xi }_j\ge 0,forallj=\mathrm{1...}n$$

对偶问题

$$\underset{x}{\min }f(x)$$
$$s.t.g(x)\le 0$$
$$h(x)=0$$
等价于求解以下两层优化（解释见后述）：$$\underset{x}{\min }\underset{\alpha \ge 0,\beta }{\max }L(x,\alpha ,\beta )$$
$L(x,\alpha ,\beta )$为拉格朗日函数：
$L(x,\alpha ,\beta )=f(x)+\alpha g(x)+\beta h(x),其中\alpha \ge 0（不等式乘子有约束）,\beta （等式乘子无约束）:为拉格朗日乘子$
推论：
$$\underset{\alpha \ge 0,\beta }{\max }L(x,\alpha ,\beta )=\{\begin{array}{ll}f(x),& \text{if }x在可行域时\\ +\infty ,& \text{if }otherwise：h(x)\ne 0org(x)>0的时候\end{array}$$
为什么这个约束问题会等价于求解两层优化的无约束问题呢？
对于拉格朗日函数$L(x,\alpha ,\beta )=f(x)+\alpha g(x)+\beta h(x)$，其中的等式约束来说，因为乘子$\beta$,其正负没有约束，无论取得x是使得$h(x)$大于0还是小于0；$\beta$都可以取对应的正无穷或者负无穷使得内层的max $\beta h(x)$正无穷大，那么外层的min根本就不起作用了，所有必须有$\beta h(x)=0$，同时，若g（x）大于0，其乘子$\alpha$大于等于0；也可以选$\alpha$正无穷大使得内层max正无穷大，这样外层的min也不起作用了，肯定不是原问题的解

强对偶:

充分条件，当原问题是凸的时候，它一定是满足强对偶的，一定可以取到等号
$$d^{\ast }=\underset{\alpha \ge 0,\beta }{\max }\underset{x}{\min }L(x,\alpha ,\beta )=\underset{x}{\min }\underset{\alpha \ge 0,\beta }{\max }L(x,\alpha ,\beta )=p^{\ast }$$

成立条件 — KKT条件

$${\nabla }_{x}L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0$$
$${\alpha }^{\ast }\ge 0$$
$$g(x^{\ast })\le 0$$
$$h(x^{\ast })=0$$
上述四个条件分别表示拉格朗日函数对x的梯度为0；${\alpha }^{\ast }\ge 0$是乘子约束要求显然是要满足的，剩下两个为解在可行域里的要求，这也是朴素自然的
所以最重要的是下面这个条件，$${\alpha }^{\ast }g(x^{\ast })=0$$
它表示了
$$\{\begin{array}{ll}{\alpha }^{\ast }>0& \text{==> }g(x^{\ast })=0约束被激活\\ g(x^{\ast })<0& \text{==> }{\alpha }^{\ast }=0约束未被激活\end{array}$$

SVM原问题与对偶问题求解

SVM模型凸优化的KKT条件成立，凸优化问题与原问题等价
原问题：
$$\underset{w,b}{\min }\frac{1}{2}{w}^{T}w$$
$$s.t.(w^T{x}_j+b)y_j\ge 1,forallj=\mathrm{1...}n$$
拉格朗日函数：
$$L(w,b,\alpha )=\frac{1}{2}{w}^{T}w-\sum _j{\alpha }_j[(w^T{x}_j+b)y_j-1]$$
$$\alpha \ge 0,\forall j$$
拉格朗日对偶函数：是拉格朗日函数关于x取得的最小值
$$L(\alpha ）={\text{inf}}_{w,b\in D}L(w,b,\alpha )=\frac{1}{2}{w}^{T}w-\sum _j{\alpha }_j[(w^T{x}_j+b)y_j-1]$$
$$\alpha \ge 0,\forall j$$
即如果拉格朗日函数关于w，b无下界，则对偶函数取值为负无穷，对偶函数构成了原问题最优值p*的下界，即对于任意的$\alpha \ge 0$都有$L(\alpha ）\le p^{\ast }$

拉格朗日函数讨论

$$\underset{x}{\min }\underset{\alpha \ge 0,\beta }{\max }L(x,\alpha ,\beta )$$为广义拉格朗日函数的极小极大问题：即线max拉格朗日乘子之后再min x；化为对偶问题，拉格朗日极大极小问题，想将两步优化的顺序倒过来，先min x，再max拉格朗日乘子，那么目标函数值是变大了还是变小了呢？
我们说是变小了，有弱对偶保证其成立
$$d^{\ast }=\underset{\alpha \ge 0,\beta }{\max }\underset{x}{\min }L(x,\alpha ,\beta )\le \underset{x}{\min }\underset{\alpha \ge 0,\beta }{\max }L(x,\alpha ,\beta )=p^{\ast }$$
证明如下：
$$记g(x)=\underset{y}{\min }f(x,y)，显然它\le f(x,y)$$
$$故有g(x)\le f(x,y)\forall y$$
$$\underset{x}{\max }g(x)\le \underset{x}{\max }f(x,y),\forall y,因为对所有的y都小于等于，故而：$$
$$\underset{x}{\max }g(x)\le \underset{y}{\min }\underset{x}{\max }f(x,y)$$
将记的g（x）代会可得：
$$\underset{x}{\max }\underset{y}{\min }f(x,y)\le \underset{y}{\min }\underset{x}{\max }f(x,y)$$
所有弱对偶条件必然成立：
$$d^{\ast }=\underset{\alpha \ge 0,\beta }{\max }\underset{x}{\min }L(x,\alpha ,\beta )\le \underset{x}{\min }\underset{\alpha \ge 0,\beta }{\max }L(x,\alpha ,\beta )=p^{\ast }$$

对偶求解

线性可分条件下

原问题：
$$\underset{w,b}{\min }\underset{\alpha \ge 0}{\max }L(w,b,\alpha )=\frac{1}{2}{w}^{T}w-\sum _j{\alpha }_j[(w^T{x}_j+b)y_j-1]$$
$$\alpha \ge 0,\forall j$$
对偶问题：
$$\underset{\alpha \ge 0}{\max }\underset{w,b}{\min }L(w,b,\alpha )=\frac{1}{2}{w}^{T}w-\sum _j{\alpha }_j[(w^T{x}_j+b)y_j-1]$$
$${\alpha }_j\ge 0,\forall j$$

先对对偶问题的内层进行优化：
$$\frac{\partial L(w,b,\alpha )}{\partial w}=w-\sum _j{\alpha }_j{x}_j{y}_j=0\to w=\sum _j{\alpha }_j{x}_j{y}_j$$
$$\frac{\partial L(w,b,\alpha )}{\partial b}=-\sum _j{\alpha }_j{y}_j=0\to \sum _j{\alpha }_j{y}_j=0$$
将内层优化的驻点代入对偶问题：
$$\underset{\alpha \ge 0}{\max }L(\alpha )=\frac{1}{2}(\sum _i{\alpha }_i{x}_i{y}_i{)}^T(\sum _j{\alpha }_j{x}_j{y}_j)-\sum _j{\alpha }_j[((\sum _i{\alpha }_i{x}_i{y}_i{)}^T{x}_j+b)y_j-1]$$
$$=\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j-\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j-\sum _j{\alpha }_j{y}_{j}b+\sum _j{\alpha }_j$$
此处${\sum }_j{\alpha }_j{y}_{j}b=0$
$$\underset{\alpha \ge 0}{\max }L(\alpha )=-\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j+\sum _j{\alpha }_j$$
亦即：
$$\underset{\alpha \ge 0}{\min }L(\alpha )=\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j-\sum _j{\alpha }_j$$
$$s.t.\sum _j{\alpha }_j{y}_j=0,{\alpha }_j\ge 0$$

线性可分情况下对偶问题：
$$\underset{\alpha \ge 0}{\max }L(\alpha )=-\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{\text{x}}_i^T{\text{x}}_j+\sum _j{\alpha }_j$$
$$s.t.\sum _j{\alpha }_j{y}_j=0,{\alpha }_j\ge 0$$
对于$\alpha$而言也是QP问题，可直接调程序包求解
那么如何求w和b呢？【这个问题等到描述完线性不可分情况再里阐述】

线性不可分条件下

$$\underset{w,b,{\xi }_j}{\min }\frac{1}{2}{w}^{T}w+C\sum _j{\xi }_j$$
$$s.t.(w^T{x}_j+b)y_j\ge 1-{\xi }_j,forallj=\mathrm{1...}n$$
$${\xi }_j\ge 0,forallj=\mathrm{1...}n$$
原问题：
$$\underset{w,b,\xi }{\min }\underset{{\alpha }_j,{\gamma }_j\ge 0}{\max }L(w,b,,\xi ,\alpha ,\gamma )=\frac{1}{2}{w}^{T}w+C\sum _j{\xi }_j-\sum _j{\alpha }_j[(w^T{x}_j+b)y_j+{\xi }_j-1]-\sum _j{\gamma }_j{\xi }_j$$
$${\alpha }_j,{\gamma }_j\ge 0,\forall j$$
对偶问题：
$$\underset{{\alpha }_j,{\gamma }_j\ge 0}{\max }\underset{w,b,\xi }{\min }L(w,b,,\xi ,\alpha ,\gamma )=\frac{1}{2}{w}^{T}w+C\sum _j{\xi }_j-\sum _j{\alpha }_j[(w^T{x}_j+b)y_j+{\xi }_j-1]-\sum _j{\gamma }_j{\xi }_j$$
$${\alpha }_j,{\gamma }_j\ge 0,\forall j$$
先对对偶问题的内层进行优化：
$$\frac{\partial L(w,b,,\xi ,\alpha ,\gamma )}{\partial w}=w-\sum _j{\alpha }_j{x}_j{y}_j=0\to w=\sum _j{\alpha }_j{x}_j{y}_j$$
$$\frac{\partial L(w,b,,\xi ,\alpha ,\gamma )}{\partial b}=-\sum _j{\alpha }_j{y}_j=0\to \sum _j{\alpha }_j{y}_j=0$$
$$\frac{\partial L(w,b,,\xi ,\alpha ,\gamma )}{\partial {\xi }_j}=C-{\alpha }_j-{\gamma }_j=0\to C={\alpha }_j+{\gamma }_j$$
将内层优化的驻点代入对偶问题：
$$\underset{\alpha ,\gamma \ge 0}{\max }L(\alpha ,\gamma )=\frac{1}{2}(\sum _i{\alpha }_i{x}_i{y}_i{)}^T(\sum _j{\alpha }_j{x}_j{y}_j)+C\sum _j{\xi }_j-\sum _j{\alpha }_j[((\sum _i{\alpha }_i{x}_i{y}_i{)}^T{x}_j+b)y_j+{\xi }_j-1]-\sum _j{\gamma }_j{\xi }_j$$
$$=\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j-\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j-\sum _j{\alpha }_j{y}_{j}b+\sum _j{\alpha }_j+C\sum _j{\xi }_j-\sum _j{\alpha }_j{\xi }_j-\sum _j{\gamma }_j{\xi }_j$$
【此处${\sum }_j{\alpha }_j{y}_{j}b=0,C-{\alpha }_j-{\gamma }_j=0$
$C{\sum }_j{\xi }_j-{\sum }_j{\alpha }_j{\xi }_j-{\sum }_j{\gamma }_j{\xi }_j$
$C{\sum }_j{\xi }_j-{\sum }_j({\alpha }_j+{\gamma }_j){\xi }_j={\sum }_j(C-{\alpha }_j+{\gamma }_j){\xi }_j=0$】
亦即
$$\underset{\alpha ,\gamma }{\min }L(\alpha ,\gamma )=\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j-\sum _j{\alpha }_j$$
$$s.t.\sum _j{\alpha }_j{y}_j=0,{\alpha }_j\ge 0$$
$$s.t.\sum _j{\alpha }_j{y}_j=0,{\alpha }_j,{\gamma }_j\ge 0,C-{\alpha }_j-{\gamma }_j=0$$
等价于：
$$\underset{\alpha ,\gamma }{\min }L(\alpha ,\gamma )=\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j-\sum _j{\alpha }_j$$
$$s.t.\sum _j{\alpha }_j{y}_j=0,C\ge {\alpha }_j\ge 0$$
显然，上述问题仍为QP问题，对于乘子变量全是线性约束，目标函数是二次函数，可直接调程序包求解；那么如何求w和b呢？

求解w，b

线性可分条件下

求解对偶问题：$$\underset{\alpha \ge 0}{\max }L(\alpha )=-\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{\text{x}}_i^T{\text{x}}_j+\sum _j{\alpha }_j$$
$$s.t.\sum _j{\alpha }_j{y}_j=0,{\alpha }_j\ge 0$$
可以解得所有的$\alpha$,我们在对对偶问题的内层进行优化时有：
$$\frac{\partial L(w,b,\alpha )}{\partial w}=w-\sum _j{\alpha }_j{x}_j{y}_j=0\to w=\sum _j{\alpha }_j{x}_j{y}_j$$
所以可得w的求法$\text{w}={\sum }_j{\alpha }_j{\text{x}}_j{y}_j$
那么b咋求?
这就需要回到我们上面说要重点关注的KKT条件的第五个
$${\alpha }^{\ast }g(x^{\ast })=0$$
它表示了
$$\{\begin{array}{ll}{\alpha }^{\ast }>0& \text{==> }g(x^{\ast })=0约束被激活\\ g(x^{\ast })<0& \text{==> }{\alpha }^{\ast }=0约束未被激活\end{array}$$
在SVM模型中，也就是必有：
$${\alpha }_j((w^T{x}_j+b)y_j-1)=0$$
$$\{\begin{array}{ll}{\alpha }_j>0& \text{==> }(w^T{x}_j+b)y_j=1约束被激活\\ (w^T{x}_j+b)y_j>1& \text{==> }{\alpha }_j=0约束未被激活\end{array}$$
所以我们选择[一个即可]对于${\alpha }_j>0$的样本，例如${\alpha }_k>0$,其对应的样本为$(x_k,y_k)$;
有$(w^T{x}_k+b)y_k=1$,两边同时乘以$y_k$,可得：
$$w^T{x}_k+b=y_k$$
$$b=y_k-w^T{x}_k$$

求解对偶问题的意义–SVM机器学习内涵所在

如前所述，我们原问题本身就是一个QP问题，直接调用相应的求解程序包即可求解，接下来，我们从求解w，b的方式来看为什么需要转换为对偶问题：

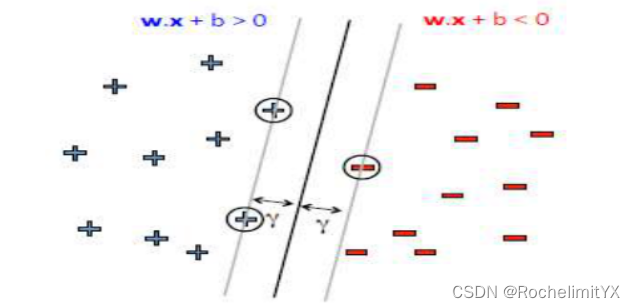
由上述，必有以下式子成立：
$${\alpha }_j((w^T{x}_j+b)y_j-1)=0$$
根据线性可分假设，如果分对了，也就是样本点在分类面类，$(w^T{x}_j+b)y_j>1$,此时样本$(x_j,y_j)$对应的${\alpha }_j=0$，根据线性可分假设，它不可能有分错的，所以当${\alpha }_j>0$样本$(x_j,y_j)$位于分类面上;由$\text{w}={\sum }_j{\alpha }_j{\text{x}}_j{y}_j$可知，对于那些${\alpha }_j=0$对应的样本，是不会出现在上述求和计算式中的，对w的值没有任何影响，同时根据计算b的讨论，想要算出b也必须使用一个${\alpha }_k>0$,其对应的样本为$(x_k,y_k)$,所以说但凡是${\alpha }_j=0$对应的样本来说，他们对ＳＶＭ模型的确定是无用的，只有落在Ｍａｒｇｉｎ上的样本点才是可能有用的，即支撑向量，只留下支撑向量，其它的数据都可以丢掉，如果我们预先能找到数据的支撑，就可以把很多的数据都丢掉，而结果是完全一样的

线性不可分条件下

求解对偶问题：
$$\underset{\alpha ,\gamma }{\min }L(\alpha ,\gamma )=\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j-\sum _j{\alpha }_j$$
$$s.t.\sum _j{\alpha }_j{y}_j=0,C\ge {\alpha }_j\ge 0$$
可以解得所有的$\alpha$和$\gamma$，我们在对对偶问题的内层进行优化时有：
$$\frac{\partial L(w,b,,\xi ,\alpha ,\gamma )}{\partial w}=w-\sum _j{\alpha }_j{x}_j{y}_j=0\to w=\sum _j{\alpha }_j{x}_j{y}_j$$
所以可得w的求法$\text{w}={\sum }_j{\alpha }_j{\text{x}}_j{y}_j$
那么b咋求?
这一样需要回到我们上面说要重点关注的KKT条件的第五个
$${\alpha }^{\ast }g(x^{\ast })=0$$
它表示了
$$\{\begin{array}{ll}{\alpha }^{\ast }>0& \text{==> }g(x^{\ast })=0约束被激活\\ g(x^{\ast })<0& \text{==> }{\alpha }^{\ast }=0约束未被激活\end{array}$$
在非线性可分SVM模型中，也就是必有：
$${\alpha }_j((w^T{x}_j+b)y_j-1+{\xi }_j)=0$$
$${\gamma }_j{\xi }_j=0$$

所以我们选择[一个即可]对于$C>{\alpha }_j>0$的样本，例如$C>{\alpha }_k>0$,此时可知${\gamma }_j=C-{\alpha }_j\ne 0;又{\gamma }_j{\xi }_j=0;{\xi }_j=0$其对应的样本为$(x_k,y_k)$;
有$(w^T{x}_k+b)y_k=1$,两边同时乘以$y_k$,可得：
$$w^T{x}_k+b=y_k$$
$$b=y_k-w^T{x}_k$$

求解对偶问题的意义–SVM机器学习内涵所在

和讨论线性可分条件下的支撑向量一样，我们现在来讨论非线性可分条件下的支撑向量是啥？

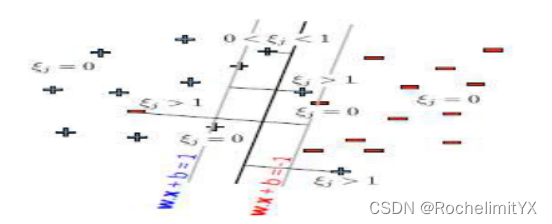
由上述，必有以下式子成立：
$${\alpha }_j((w^T{x}_j+b)y_j-1+{\xi }_j)=0$$
$${\gamma }_j{\xi }_j=0$$
对于训练数据集中的每一个样本$(x_j,y_j)$,针对解得的${\alpha }^{\ast }$，总有当${\alpha }_j=0$时，这个样本不会对f（x）有任何影响，因为由$\text{w}={\sum }_j{\alpha }_j{\text{x}}_j{y}_j$可知，对于那些${\alpha }_j=0$对应的样本，是不会出现在上述求和计算式中的，对w的值没有任何影响，同时根据计算b的讨论，想要算出b也必须使用一个$C>{\alpha }_k>0$,其对应的样本为$(x_k,y_k)$,所以说但凡是${\alpha }_j=0$对应的样本来说，他们对ＳＶＭ模型的确定是无用的，当${\alpha }_{j}neq0$时，必有$(w^T{x}_j+b)y_j-1+{\xi }_j=0$,显然这样的样本对w和b都有影响，是所谓支撑向量；
而且进一步有，如果${\alpha }_j<C$时，由$C={\alpha }_j+{\gamma }_j$,${\gamma }_j>0$,又${\gamma }_j{\xi }_j=0$，
所以$(w^T{x}_j+b)y_j=1$,也就是这个样本位于最大间隔的边界上；
如果${\alpha }_j=C$时，由$C={\alpha }_j+{\gamma }_j$,${\gamma }_j=0$,此时如果解得的对应样本的对应的${\xi }_j\le 1$，根据$(w^T{x}_j+b)y_j=1-{\xi }_j$,即$1\ge (w^T{x}_j+b)y_j\ge 0$根据线性可分假设，这样的样本也是分对了的，但是位于最大间隔的内部；如果解得的对应样本的对应的${\xi }_j>1$,根据$(w^T{x}_j+b)y_j=1-{\xi }_j$,即$(w^T{x}_j+b)y_j<0$根据线性可分假设，这样的样本也是分错了的；
综上，我们得到支撑向量，位于最大间隔边界上的点，位于边界内的点，分错了的点
依然地只留下支撑向量，其它的数据都可以丢掉，如果我们预先能找到数据的支撑，就可以把很多的数据都丢掉，而结果是完全一样的

再看SVM目标函数

可将目标函数视为损失加正则的模式；$$\underset{w,b,{\xi }_j}{\min }\frac{1}{2}{w}^{T}w+C\sum _j{\xi }_j$$
$$s.t.(w^T{x}_j+b)y_j\ge 1-{\xi }_j,forallj=\mathrm{1...}n$$
$${\xi }_j\ge 0,forallj=\mathrm{1...}n$$
且可以将上述问题用hinge损失重写为
$$\underset{w,b,{\xi }_j}{\min }\frac{1}{2}{w}^{T}w+C\sum _j\max (0,1-(w^T{x}_j+b)y_j)$$
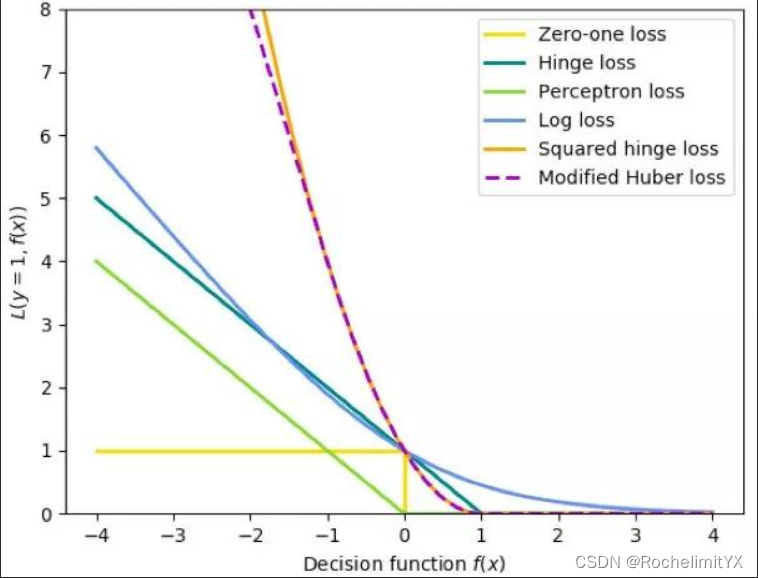
此处损失还可以为其它形式：

核化技巧

如数据非线性可分时，该怎样使用SVM？
朴素自然的思想：变非线性为线性–核方法
在低维空间计算获得高维空间的计算结果，满足高维，才能在高维下线性可分。 我们需要引入一个新的概念：核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。这样我们就可以使用原来的推导来进行计算，只是所有的推导是在新的空间，而不是在原来的空间中进行，即用核函数来替换当中的内积。

对偶问题

$$\underset{\alpha ,\gamma }{\min }L(\alpha ,\gamma )=\frac{1}{2}\sum _i\sum _j{\alpha }_i{y}_i{\alpha }_j{y}_{j}K(x_i,x_j)-\sum _j{\alpha }_j$$
$$K(x_i,x_j)=\Phi (x_i).\Phi (x_j)$$
$$s.t.\sum _j{\alpha }_j{y}_j=0,C\ge {\alpha }_j\ge 0$$
即通过一个非线性转换后的两个样本间的内积。具体地，𝐾(𝑥, 𝑧)是一个核函数，或正定核，
意味着存在一个从输入空间到特征空间的映射，对于任意空间输入的𝑥, 𝑧 有:𝐾(𝑥, 𝑧) = 𝜙(𝑥) ⋅ 𝜙(𝑧)
注记：原问题或者对偶问题的x不能是单一出现的，只能是以内积的形式
典型核函数：

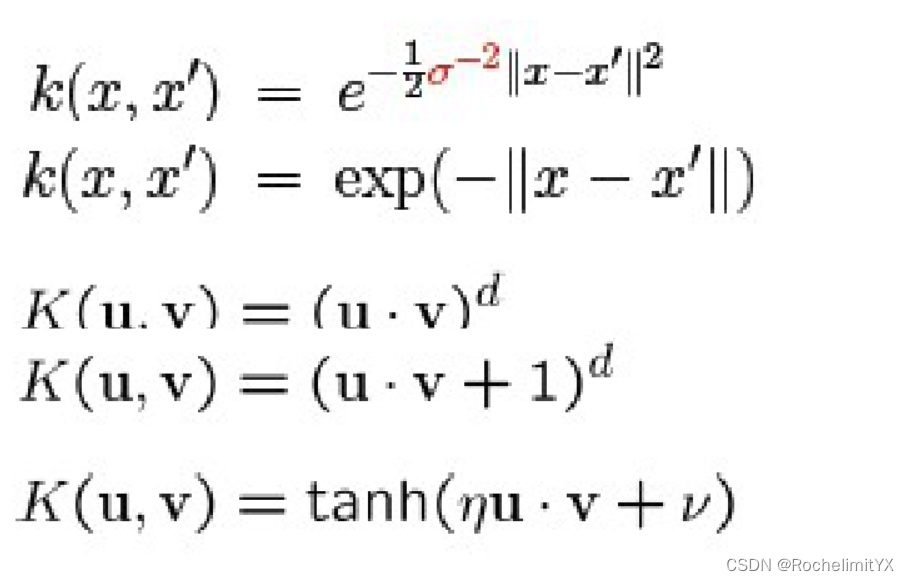
求解w，b

$\text{w}={\sum }_j{\alpha }_j{y}_j\Phi (x_j)$
$b=y_k-w.\Phi (x_j),其中k满足,C>{\alpha }_k>0,任选一个样本即可$
$f(x)=sign(\text{w}.\Phi (x)+b)$

小结

支撑向量机作为传统机器学习方法的集大成者，其在数学理论的正确性核优美性是我们所追求的，在对偶问题下看清SVM作为机器学习方法的本质内涵，更应该是我们所推崇的，接下来的一篇将继续SVM，探讨由核函数引出的超参数调整方法以及其引发的统计学习理论的快速发展，使得机器学习有了深刻的理论支持，就如那支撑向量之于训练数据集的重要性一样。