Pytroch光流基础（forward_flow、backward_flow、遮挡掩码 occlusion mas、光流warp、forward-backward consistency check）

Reference：Opencv、UnFlow、RAFT、GMFlow、Back to Basics、AccFlow

本文仅讨论稠密光流（对图像中的每个像素点都计算光流），而不讨论那些基于特征点的稀疏光流（仅计算图像中特征点的光流）。如果想了解两者的区别看这篇。本文的代码注意来自gmflow。

0. 前置知识 Image Warping

推荐阅读：
关于Image Warping的理解与实现
【video frame interpolation系列1】背景知识: forward and backward image warping （图像扭曲/变换）
【VFI系列2】视频内插帧中基于optical flow的 backward/forward warping

在理解flow_warping之前，需要先学习Image Warping（一种图像Transform的算法）：

• Forward Warping的原理（正变换：把source_image中点的值直接warp到destination_image中对应点上）：遍历source image中的每个点p_source，乘以从source image到destination image的affine matrix，将其投影到destination image中得到p_destination，如果p_destination的坐标不是整数，则进行四舍五入取整，这必然会产生问题：**destination image中有的位置没有从source image中投影过来的点，有的位置有多个从source image中投影过来的点，所以会产生很多空洞，产生类似波纹的效果。
  
  

• Backward Warping的原理（反变换+插值：把destination_image中的点warp到source_image对应点上，找最近的点的值）：遍历destination image中的每个点p_destination，乘以destination image到source image的affine matrix，得这个点在source image中的对应点p_source，令p_destination的像素值等于p_source的值，如果p_source的坐标不是整数，则采用插值逼近的方法进行近似，因此不会产生的Forward Warping的问题。

1. 光流定义（optical flow）

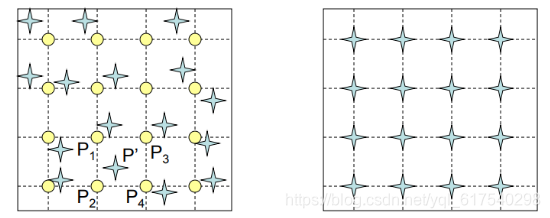
光流是一个二维速度场，表示 每个像素pixel 从参考图像到目标图像的运动偏移。光流的数学定义如下：给定两个图像$img1,img2\in R^{H\times W\times 3}$，$flow\in R^{H\times W\times 2}$，其中channel=2分别描述 img1和 img2之间的水平和垂直图像像素的位移值。光流的表示也是数字化的。它一般使用一个三维数组(H, W, 2) 表示，其中H表示图像的高度，也就是数组中的行数，W表示图像的宽度，也就是数组中的列数，2表示x,y两个方向。

举个例子，第 t 帧的时候A点的位置是(x1, y1)，那么我们在第t+1帧的时候再找到A点，假如它的位置是(x2,y2)，那么我们就可以确定A点的运动了：(ux, vy) = (x2, y2) - (x1,y1)。

• 在光流数组的第三维上，第一通道（即[height,width,0]）表示图像在x方向的偏移方向和大小。这里的x方向是水平方向，即图像数组中的行向量方向；
• 第二通道（即[height,width,1]）表示图像在y方向的偏移方向和大小。这里的y方向是竖直方向，即图像数组中的列向量方向。

这里还要注意的一点：像素坐标偏移量的大小当然就是通过光流数组中的数值大小体现出来的，而偏移的方向是通过光流数组中的正负体现出来的。在x方向上，正值表示物体向左移动，而负值表示物体向右移动；在y方向上，正值表示物体向上移动，而负值表示物体向下移动。

至于为什么是这样的，后面我们在backward warp中的源码中进行解释。

为了能真实感受光流，以及它的格式。这里写了一个小代码来生成一个由一个点向四周扩散的光流，这里的光流数组的shape为[ 11 , 11 , 2 ]，如下图（光流的可视化下面讲解）：

# 第一通道
[[ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]
 [ 2.5  2.   1.5  1.   0.5  0.  -0.5 -1.  -1.5 -2.  -2.5]]
# 第二通道
[[ 2.5  2.5  2.5  2.5  2.5  2.5  2.5  2.5  2.5  2.5  2.5]
 [ 2.   2.   2.   2.   2.   2.   2.   2.   2.   2.   2. ]
 [ 1.5  1.5  1.5  1.5  1.5  1.5  1.5  1.5  1.5  1.5  1.5]
 [ 1.   1.   1.   1.   1.   1.   1.   1.   1.   1.   1. ]
 [ 0.5  0.5  0.5  0.5  0.5  0.5  0.5  0.5  0.5  0.5  0.5]
 [ 0.   0.   0.   0.   0.   0.   0.   0.   0.   0.   0. ]
 [-0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5]
 [-1.  -1.  -1.  -1.  -1.  -1.  -1.  -1.  -1.  -1.  -1. ]
 [-1.5 -1.5 -1.5 -1.5 -1.5 -1.5 -1.5 -1.5 -1.5 -1.5 -1.5]
 [-2.  -2.  -2.  -2.  -2.  -2.  -2.  -2.  -2.  -2.  -2. ]
 [-2.5 -2.5 -2.5 -2.5 -2.5 -2.5 -2.5 -2.5 -2.5 -2.5 -2.5]]

光流提取

• 相邻帧光流：为了提取光流，一般就需要输入视频中的相邻两帧，或者图像序列中的相邻两张图像，然后通过算法提取出光流。算法包括传统方法（OpenCV内置算法），也有目前基于深度学习的方法，比如FlowNet、RAFT、GMFlow等。由于提取光流的算法不是本文的重点，这里就不进行赘述。

# 可以通过Opencv的函数cv2.calcOpticalFlowFarneback寻找稠密光流，我们得到的一个两个通道的向量(u,v)。得到的该向量的大小和方向。用不同的颜色编码来使其可视化。
import cv2 as cv
import numpy as np
output_video_path = "flow.mp4"
cap = cv.VideoCapture("/home/yzr/data/Cartoon2Real/test1.mp4")
fourcc = cv.VideoWriter_fourcc(*'mp4v')  # 使用 MP4V 编码器
fps = cap.get(cv.CAP_PROP_FPS)  # 获取源视频帧率
frame_width = int(cap.get(cv.CAP_PROP_FRAME_WIDTH))  # 获取源视频宽度
frame_height = int(cap.get(cv.CAP_PROP_FRAME_HEIGHT))  # 获取源视频高度
out = cv.VideoWriter(output_video_path, fourcc, fps, (frame_width, frame_height))

ret, frame1 = cap.read()
prvs = cv.cvtColor(frame1, cv.COLOR_BGR2GRAY)
hsv = np.zeros_like(frame1)
hsv[..., 1] = 255
while True:
    ret, frame2 = cap.read()
    if not ret:
        break
    next = cv.cvtColor(frame2, cv.COLOR_BGR2GRAY)
    # 返回一个两通道的光流向量，实际上是每个点的像素位移值
    flow = cv.calcOpticalFlowFarneback(prvs, next, None, 0.5, 3, 15, 3, 5, 1.2, 0)
    # 笛卡尔坐标转换为极坐标，获得极轴和极角
    mag, ang = cv.cartToPolar(flow[..., 0], flow[..., 1])
    hsv[..., 0] = ang * 180 / np.pi / 2  # 角度
    hsv[..., 2] = cv.normalize(mag, None, 0, 255, cv.NORM_MINMAX)
    bgr = cv.cvtColor(hsv, cv.COLOR_HSV2BGR)
    # 将处理后的帧写入输出视频
    out.write(bgr)
    prvs = next

cap.release()
out.release()
cv.destroyAllWindows()

• 跨帧光流：估计间隔多帧的两张图像之间的长程光流，特别是在复杂的物体变形和大运动遮挡下十分困难，目前的解决方案是显式或隐式地累积相邻帧的光流，以获得所需的长程光流，如AccFlow。

光流可视化

使用 flow_to_image 实现 flow_array 的可视化。这里放一个make_color_wheel代码的运行结果，还是上面展示的那个光流，唯一区别就是这里的光流数组大小为[101, 101, 2]， 这个也是Color Wheel，它的作用就是给你一个由该代码生成的光流可视化图，你参考这个Color Wheel就会知道物体的偏移方向和大小，例如绿色就代表往右上角偏移，而颜色的深度就表示偏移的大小：

def make_color_wheel():
    """
    Generate color wheel according Middlebury color code
    :return: Color wheel
    """
    RY = 15
    YG = 6
    GC = 4
    CB = 11
    BM = 13
    MR = 6

    ncols = RY + YG + GC + CB + BM + MR

    colorwheel = np.zeros([ncols, 3])

    col = 0

    # RY
    colorwheel[0:RY, 0] = 255
    colorwheel[0:RY, 1] = np.transpose(np.floor(255*np.arange(0, RY) / RY))
    col += RY

    # YG
    colorwheel[col:col+YG, 0] = 255 - np.transpose(np.floor(255*np.arange(0, YG) / YG))
    colorwheel[col:col+YG, 1] = 255
    col += YG

    # GC
    colorwheel[col:col+GC, 1] = 255
    colorwheel[col:col+GC, 2] = np.transpose(np.floor(255*np.arange(0, GC) / GC))
    col += GC

    # CB
    colorwheel[col:col+CB, 1] = 255 - np.transpose(np.floor(255*np.arange(0, CB) / CB))
    colorwheel[col:col+CB, 2] = 255
    col += CB

    # BM
    colorwheel[col:col+BM, 2] = 255
    colorwheel[col:col+BM, 0] = np.transpose(np.floor(255*np.arange(0, BM) / BM))
    col += + BM

    # MR
    colorwheel[col:col+MR, 2] = 255 - np.transpose(np.floor(255 * np.arange(0, MR) / MR))
    colorwheel[col:col+MR, 0] = 255

    return colorwheel

def compute_color(u, v):
    """
    compute optical flow color map
    :param u: optical flow horizontal map
    :param v: optical flow vertical map
    :return: optical flow in color code
    """
    [h, w] = u.shape
    img = np.zeros([h, w, 3])
    nanIdx = np.isnan(u) | np.isnan(v)
    u[nanIdx] = 0
    v[nanIdx] = 0

    colorwheel = make_color_wheel()
    ncols = np.size(colorwheel, 0)

    rad = np.sqrt(u**2+v**2)

    a = np.arctan2(-v, -u) / np.pi

    fk = (a+1) / 2 * (ncols - 1) + 1

    k0 = np.floor(fk).astype(int)

    k1 = k0 + 1
    k1[k1 == ncols+1] = 1
    f = fk - k0

    for i in range(0, np.size(colorwheel,1)):
        tmp = colorwheel[:, i]
        col0 = tmp[k0-1] / 255
        col1 = tmp[k1-1] / 255
        col = (1-f) * col0 + f * col1

        idx = rad <= 1
        col[idx] = 1-rad[idx]*(1-col[idx])
        notidx = np.logical_not(idx)

        col[notidx] *= 0.75
        img[:, :, i] = np.uint8(np.floor(255 * col*(1-nanIdx)))

    return img

def flow_to_image(flow):
    """
    Convert flow into middlebury color code image
    :param flow: optical flow map
    :return: optical flow image in middlebury color
    """
    u = flow[:, :, 0]
    v = flow[:, :, 1]

    maxu = -999.
    maxv = -999.
    minu = 999.
    minv = 999.
    UNKNOWN_FLOW_THRESH = 1e7
    SMALLFLOW = 0.0
    LARGEFLOW = 1e8

    idxUnknow = (abs(u) > UNKNOWN_FLOW_THRESH) | (abs(v) > UNKNOWN_FLOW_THRESH)
    u[idxUnknow] = 0
    v[idxUnknow] = 0

    maxu = max(maxu, np.max(u))
    minu = min(minu, np.min(u))

    maxv = max(maxv, np.max(v))
    minv = min(minv, np.min(v))

    rad = np.sqrt(u ** 2 + v ** 2)
    maxrad = max(-1, np.max(rad))

    u = u/(maxrad + np.finfo(float).eps)
    v = v/(maxrad + np.finfo(float).eps)

    img = compute_color(u, v)

    idx = np.repeat(idxUnknow[:, :, np.newaxis], 3, axis=2)
    img[idx] = 0
    return np.uint8(img)
    
img = flow_to_image(flow)
plt.imshow(img)
plt.show()

【通俗易懂】详解torch.nn.functional.grid_sample函数：可实现对特征图的水平/垂直翻转

Unsupervised Optical Flow

由于真实数据的Optical flow的label很难得到，成本大，目前，一般在非真实的生成数据上进行监督训练（生成数据的Optical flow的label比较容易生成）。基于这个原因，研究如何在真实数据上通过unsupervised方式来直接训练，是有意义的。

• 前提假设：在前后两帧图片里面，物体的外形没有发生太大的变化。

• 模型：设计一个CNN模型来预测前后两帧之间的flow。

• 训练：通过模型计算出来的flow，对图片进行warp变换，来跟另外一张图片匹配，计算出某种loss，通过loss来训练。
  

• Naive的 Loss：给定相邻2帧 图片0 $I^{(0)}$, 图片1 $I^{(1)}$，模型预测得到图像$I^{(0)}$中每个像素对于图像$I^{(1)}$的偏移量$F_{0\to 1}=f_{\theta }(I^{(0)},I^{(1)})$。当我们已知 $I^{(0)}$和$F_{0\to 1}=f_{\theta }(I^{(0)},I^{(1)})$时，我们就可以warp得到一个假的图片1：$warp(I^{(0)},F_{0\to 1})$，这样就可以计算loss了：$L(warp(I^{(0)},F_{0\to 1}),I^{(1)})$
  

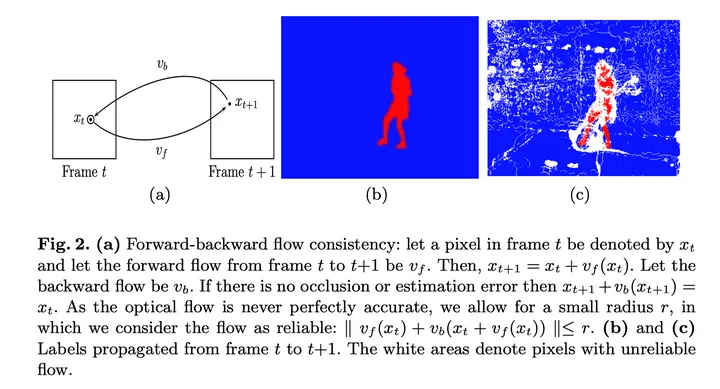
• 考虑Occlusion mask的 Loss：在计算loss时，为了只计算有效像素点的loss而忽略哪些无效的像素点，还需要训练一个额外的模型来学习occlusion mask，来标记每个像素的有效性：因为在实际情况下，由于遮挡的问题（一些像素只在 图片0 $I^{(0)}$ 里面存在，而在图片1 $I^{(1)}$ 中没有对应的像素），这类像素，在计算loss时，是不应该考虑的。 由于我们的遮挡检测还需要反向光流$F_{1\to 0}$，因此通过使所有loss项对称（即，为两个flow方向计算它们）来联合估计双向光流。这样就可以用前后一致性假设forward-backward consistency check 得到双向的occlusion mask：$O_f,O_b=g(F_{0\to 1},F_{1\to 0})$，对于I0未遮挡的像素x，使用forward_flow warp到I1相应像素处，再使用backward_flow warp回来，像素应该回到该像素位于原图的原先位置。 每当这两个流之间的不匹配时，我们将像素标记为被遮挡。
  

2. 双向光流 bidirectional flow（forward_flow, backward_flow）

前向光流 forward_flow，后向光流 backward_flow 都是以当前帧$I_t$做参考帧，所以在可视化的时候，前向和后向应该物体轮廓的位置都一样,可视化效果是差不多的。

• 前向 forward flow： $I_t\to I_{t+1}$的像素偏移，以$I_t$为基坐标
• 后向 backward flow：$I_t\to I_{t-1}$的像素偏移，以$I_t$为基坐标
  

3. 光流映射 backward warp

Pytorch实现warping操作
Pytorch光流warp函数解读（grid_sample函数的使用)

通过输入的两个参考帧$I_0$, $I_1$，基于光流估计算法得到双向光流（bi-directional optical flow），forward_flow记为$F_{0\to 1}$和backward_flow记为$F_{1\to 0}$：

根据本文最开始的Image Warping可知（backward warp）：

• 有了$I_0$和$F_{1\to 0}$，我们可以将$I_0$和反向光流$F_{1\to 0}$进行warping操作，得到$I_1$。
• 有了$I_1$和$F_{0\to 1}$，我们可以将$I_1$和前向光流$F_{0\to 1}$进行warping操作，得到$I_0$。

注意：backward warp和是否使用backward_flow无关，backward warp指的是从图像A warp 到图像B, 使用从B到A的光流$F_{A\to B}$!!!

warp算法的基础就是光度一致性：$I_1(x,y)=I_2(x+u,y+v)$，相邻帧之间的光流对应像素值相同：

• input：img2，forward_flow
• output：warped_img2 (如果flow完全正确，warped_img2应该与img1相同)

def flow_warp(feature, flow, mask=False, padding_mode='zeros'):
	'''
    backward warp: use flow to warp feature
        feature : [B, C, H, W]
        flow : [B, 2, H, W]
        if feature 来自前一帧的image/feature：flow 使用backward_flow
        	grid + flow: img1的每个像素坐标 + 光流flow = 即为img1中该像素点对应在img2的坐标
        if feature 来自后一帧的image/feature：flow 使用forward_flow
        	grid + flow: img2的每个像素坐标 + 光流flow = 即为img2中该像素点对应在img1的坐标
    '''
    b, c, h, w = feature.size()  # feature/image size [B, C, H, W]
    assert flow.size(1) == 2  # x flow and y flow

    # 1. get coords grid
    y, x = torch.meshgrid(torch.arange(h), torch.arange(w))  # [H, W]
    grid = torch.stack([x, y], dim=0).float()  # [2, H, W]
    grid = grid[None].repeat(b, 1, 1, 1)  # [B, 2, H, W]

    # 2. vgrid = grid + flow
    vgrid = grid.to(flow.device) + flow  # sample_coords: [B, 2, H, W] in image scale

    # 3. bilinear sampling
    if vgrid.size(1) != 2:  # [B, H, W, 2]
        vgrid = vgrid.permute(0, 3, 1, 2)  # [B, 2, H, W]
    # scale grid to [-1,1] : 2*coords/(coords_max_value-1) - 1 in [-1,1]
    x_grid = 2 * vgrid[:, 0] / (w - 1) - 1
    y_grid = 2 * vgrid[:, 1] / (h - 1) - 1
    vgrid = torch.stack([x_grid, y_grid], dim=-1)  # shape=[B, H, W, 2] for grid_sample
    img = F.grid_sample(img, vgrid, mode='bilinear', padding_mode=padding_mode, align_corners=True)
    if mask:  # mask过滤超出边界的点，并非occ_mask
        mask = (x_grid >= -1) & (y_grid >= -1) & (x_grid <= 1) & (y_grid <= 1)  # [B, H, W]
        return img, mask
    return img

将meshgrid加上光流后的grid记作vgrid, 代表第二帧每个像素对应第一帧上的那个位置（这个位置可能是小数、甚至超出图像边界）：如img1中(i,j)位置的像素 = img2中 (vgrid[0][i][j], vgrid[1][i][j])位置的像素

	def warp(x, flo):
        """
        warp an image/tensor (im2) back to im1, according to the optical flow
        x: [B, C, H, W] (im2)
        flo: [B, 2, H, W] flow
        """
        B, C, H, W = x.size()
        # mesh grid 
        xx = torch.arange(0, W).view(1,-1).repeat(H,1)
        yy = torch.arange(0, H).view(-1,1).repeat(1,W)
        xx = xx.view(1,1,H,W).repeat(B,1,1,1)  # (B,1,H,W)
        yy = yy.view(1,1,H,W).repeat(B,1,1,1)  # (B,1,H,W)
        grid = torch.cat((xx,yy),dim=1).float()  # (B,2,H,W)
        x, grid = x.cuda(), grid.cuda()
        
        # img2的每个像素坐标 + 光流flo = 即为该像素点对应在img1的坐标
        vgrid = Variable(grid) + flo  # (B,2,H,W)
		 # scale grid to [-1,1] 
		 # 取出光流v这个维度，原来范围是0~W-1，再除以W-1，范围是0~1，再乘以2，范围是0~2，再-1，范围是-1~1
        vgrid[:,0,:,:] = 2.0*vgrid[:,0,:,:].clone()/max(W-1,1)-1.0 
        # 取出光流u这个维度，，原来范围是0~H-1，再除以H-1，范围是0~1，再乘以2，范围是0~2，再-1，范围是-1~1
        vgrid[:,1,:,:] = 2.0*vgrid[:,1,:,:].clone()/max(H-1,1)-1.0 
		
		# reshape (B,2,H,W) -> (B,H,W,2) 为什么要这么变呢？是因为要配合grid_sample这个函数的使用
        vgrid = vgrid.permute(0,2,3,1)
        output = nn.functional.grid_sample(x, vgrid,align_corners=True)
        mask = torch.autograd.Variable(torch.ones(x.size())).cuda()
        mask = nn.functional.grid_sample(mask, vgrid,align_corners=True)

		 ##2019 author
        mask[mask<0.9999] = 0
        mask[mask>0] = 1

		 ##2019 code
		 # mask = torch.floor(torch.clamp(mask, 0 ,1))

		 return output*mask

可选的有两种分别是nearest 或者 bilinear。 就是两种插帧方式，为什么需要插值？是因为坐标变换后，很多坐标上并没有相应的原始像素与之对应，需要通过插值来处理

grid_sample

output=torch.nn.functional.grid_sample(input, grid, mode='bilinear', padding_mode='zeros')
	input [N,C=3,H,W]
	output [N,H,W,2]
	output [N,C=3,H,W]

对于output上的每一点，(x, y)坐标处的三个通道的像素值，采集自input上某一点(x0,y0)坐标三个通道的像素值，采集的点存在于grid最低维，也就是(N, H, W, 2)中的2分别是x坐标的索引和y坐标的索引, [0]索引到input的x坐标，[1]索引到input的y坐标。在grid[0]中查找x0，在grid[1]中查找y0。

即对于output的每个位置output[:,x,y]的三通道像素值，是由grid[x,y]指定的x0,y0坐标，去input中对应的位置插值input[:,x0,y0]得到的三通道像素值。

对于output中的每一个像素(x, y)，它会根据flow流值在input中找到对应的像素点(x+u, y+v)，并赋予自己对应点的像素值，这便完成了warp操作。但这个对应点的坐标不一定是整数值，因此要用到插值或者使用邻近值，也就是选项mode的作用。

那么如何找到对应像素点呢？ 关键的过程在于grid，若grid(x,y)的两个通道值为( x0, y0 )，则表明output(x,y)的对应点在input的(x0, y0)处。但这里一般会将x0和y0的取值范围归一化到[-1, 1]之间，[-1, -1]表示input左上角的像素的坐标，[1, 1]表示input右下角的像素的坐标，对于超出这个范围的坐标，函数将会根据参数padding_mode的设定进行不同的处理。

4. 遮挡掩码 occlusion mask

遮挡掩码（Occlusion Mask）：遮挡掩码用于表示图像中被其他物体或者场景元素遮挡的区域（在前一帧中存在，但在后一帧中不存在的像素）。在光流估计中，由于物体的运动和相机的移动，可能会出现遮挡现象，即某些像素在连续帧中被其他物体或场景遮挡，导致无法准确计算其光流，光流Flow和遮挡Occlusion的“鸡蛋相生”关系（光流估计需要了解遮挡，而遮挡又与光流相关）。为了排除这些遮挡区域对光流估计的影响，需要使用遮挡掩码来标记这些区域，在后续处理中将其排除。遮挡掩码通常是一个二进制图像，其中被遮挡的区域被标记为1，未被遮挡的区域被标记为0。occlusion mask可以使用双向光流的一致性检验进行计算，具体在第5节中介绍。

因为遮挡会导致warp算法模糊错位：根据所示的流程，将顶部图像扭曲到底部图像。前景对象（阴影区域）生成一个较大的位移（由红线跟踪），而背景则保持静止（由蓝线跟踪）。然而，一个前景物体的副本在扭曲后仍然停留在被遮挡的区域。因此使用Occlusion Mask来辅助光流warp就十分必要了！

5. 前后一致性检查（forward-backward consistency check）

普遍认为基于前向和反向光流(双向光流)的 forward-backward consistency assumption 可以很好地将遮挡区域occlusion mask标出来，部分论文也称 forward-backward consistency check。

最上面图 (e) 绿色的线是 forward flow，用 $v_f(x^t)$ 表示；图 (g) 紫色的线是 backward flow，用 $v_b(x^t)$ 表示；$x^t$ 指图片中的某一个像素，图 (a) 和图 (b) 是连续两帧。

对于 (a) 中未遮挡的像素x，使用forward_flow warp到 (b) 相应像素处，再使用backward_flow warp回来，像素应该回到该像素位于原图的原先位置。 每当这两个流之间的不匹配时，我们将像素标记为被遮挡：

6. 代表模型：RAFT vs GMFlow

先前以RAFT为代表的模型 vs GMFlow：

• RAFT基于CNN的局部特征提取光流，而GMFlow基于Transformer的全局特征提取光流

• 计算双向光流时（bidirectional flow：forward_flow和backward_flow），RAFT需要对调输入图片的顺序进行2次模型推理，分别计算forward_flow和backward_flow；而GMFlow只需要1次模型推理(通过直接转置方程式中的全局相关矩阵来简化backward_flow计算)，即可得到forward_flow和backward_flow。（双向光流可以根据forward-backward consistency check，来计算occlusion mask）
  
  

7. 跨帧光流 AccFlow

假设现在有一个T帧的视频，并有T-1个预先获得的帧间光流 { F t → t + 1 ∣ t = 1 , . . . , T − 1 } \{F_{t\to t+1}|t=1,...,T-1\} {Ft→t+1​∣t=1,...,T−1} 。我们这些帧间光流不断累加即可获得长距离的跨帧光流。现在考虑两个光流的累加过程，可以分为两个步骤：首先，将两个光流向量的起点对齐；然后，将两个向量的值相加。这两个步骤中，难度较大的是对齐的过程，因为这其中存在由warping操作导致的遮挡问题。

如上图所示，我们将累积看作是红色箭头与蓝色箭头的相加。而黄色的虚线箭头，则代表着对齐距离。如果需要对齐的两帧在时间上的跨度较大，通常运动也就越大，而更大的运动则会导致更大的遮挡问题。因此，前向累积的遮挡问题随着时间的增加而逐渐增加。相比之下，反向累积的过程，我们发现对齐距离与时间无关，并始终保持最小值。我们统计了5000个数据下的遮挡比例，给出不同帧间间隔下（Δ）遮挡比例的统计如下: