使用多元线性回归和时间序列模型对人口老龄化进行分析
摘 要: 本文对计划生育之后的中国人口老龄化进行了研究分析,研究影响人口老龄化的因素。为此,从国家统计局官网中国统计年鉴中整理出了1990-2019年的连续的人口增长率及其相关指标数据,如国民总收入(亿元),居民消费支出(元),人口老龄化(%)和公共预算收入增长率(%)。对数据进行了描述性分析和相关分析,并用R语言建立了多元线性回归模型,并对建立的模型进行分析,并处理的模型的多重共线性问题。最终得出结论,揭露了一些因素对人口老龄化的影响,其中显著性的因素是居自然增长率 和国民总收入。
1研究背景
21世纪是人口老龄化的时代。目前,我国65岁及以上老人所占比重已经接近10%,人口老龄化问题关乎我国未来经济社会的长远发展,必须对当前我国人口老龄化的趋势及可能带来的影响进行深入分析,以便及时调整相应的政策和措施加以应对。
2数据来源
全部数据来源于国家统计局官网中国统计年鉴,通过整理收集获得,数据是1990-2019年的连续的人口增长率及其相关指标数据,如国民总收入(亿元),居民消费支出(元),人口老龄化(%)和公共预算收入增长率(%)。
收集的网址是:http://www.stats.gov.cn/tjsj/ndsj/
收集到的信息整理成如下图2.1所示:

图2.1 数据集
根据搜集的数据,为了更加全面的了解人口增长率的影响因素,选择人口自然增长率为解释变量,以此来反映人口增长。选择国民总收入(亿元),居民消费支出(元),人口老龄化(%)和公共预算收入增长率(%)作为增长的指标。鉴于收集到的数据,暂且考虑这些影响因素。根据以上数据,建立中国自然增长率的多元线性回归模型。
3描述性分析
3.1统计分析
基于收集到的数据,通过R语言的psych包中的describe进行统计分析,它可以计算非缺失值的数量、平均数、标准差、中位数、截尾均值、绝对中位差、最小值、最大值、值域、偏度、峰度和平均值的标准误差,如表3.1 所示。
图3.1 统计分析表

基于上表可以得出1990-2019年的人口增长率的平均值是7.44,标准差是2.88,最小值是3.32、最大值14.39等相关信息。
3.2趋势可视化
基于人口增长率(%),国民总收入(亿元),居民消费支出(元),人口老龄化(%)和公共预算收入增长率(%)都是不同年份的指标,因此可以绘制对应的趋势图来查看近几年的变化趋势。上述指标的变化趋势绘制的图形在表3.2整理而出。
图3.2变量趋势表

从表3.2得出,和人口老龄化的趋势相同(或者趋势相反的)的指标分别是国民总收入,居民消费支出和人口增长率,因此初步分析人口老龄化和国民总收入,居民消费支出和人口增长率的因素相关,和公共预算收入增长率无关。
3.3散点图矩阵
基于上面的趋势分析,绘制了相关的散点图矩阵,通过PerformanceAnalytics包中的 chart.Correlation函数就可以绘制出来。

图3.1 散点相关图
通过图3.1,可以分析得出人口老龄化与国民总收入和居民消费支出的相关系数分别是0.98,0.99。相关程度比较大,属于强正相关。人口老龄化与公共预算收入增长率和人口自然增长率相关系数是-0.43和-0.78,属于强负相关。
4 回归分析
回归通指那些用一个 或多个预测变量(也称自变量或解释变量)来预测响应变量(也称因变量、效标变量或结果变量) 的方法。通常,回归分析可以用来挑选与响应变量相关的解释变量。
本文使用的数据均来自中国统计年鉴1990-2019当年的各项数据。结合影响人口老龄化的主要因素,笔者选取了我国人口自然增长率,国民总收入,居民消费支出和公共预算收入增长率共四个指标进行多元回归分析,考虑到 国民总收入和居民消费支出比较大,都进行除以1000000的处理。因变量人口老龄化取对数操作。
将获得的数据带入模型中,并且利用R语言进行数据分析,最终得出的多元线性回归模型的结果,如下图4.1所示。

图4.1 线性模型结果
当预测变量不止一个时,回归系数的含义为:一个预测变量增加一个单位,其他预测变量保持不变时,因变量将要增加的数量。例如本例中,人口自然增长率的回归系数为-0.0239938,表示国民总收入,控制居民消费支出和公共预算收入增长率不变时,人口自然增长率上升1个单位,人口老龄化预计将会减小1.024284,它的系数系数p是显著不为0(p=0.0000)。
对老龄化系数与各影响因素的多元回归结果进行整理,结果如下表4.1所示。
表4.1 老龄化系数与各影响因素的多元回归结果

最终得出的多元线性回归模型为:
总体来看,拟合优度是0.9923,校正拟合优度是0.9911。所有的预测变量解释了人口老龄化99.11%的方差。线性模型结果告诉了,显著的因素是人口自然增长率和居民消费支出。主要是根据Pr(>|t|)是否小于0.05判断的,其中人口自然增长率和国民总收入的系数的p值是小于0.05,因此认为是显著的,而居民消费支出和公共预算收入增长率的估计的系数的p值是大于0.05,因此认为是不显著的。
人口老龄化与人口自然增长率有关是因为,自然增长率=出生率-死亡率,所以自然增长率反映了国家或地区的新增人口的比例,自然增长率越高,说明青少年比例大。人口老龄化会在短期内使劳动年龄人口减少而消费性的人口相对增多,但前者创造财富,从而导致居民消费率的短期内增加。老龄化会促进“银发经济”的快速发展,老龄人口的消费倾向较高,人口老龄化的加快会带来医疗、卫生、养老、健康消费方面支出的增加。从模型的实际意义分析,要想降低人口老龄化需要鼓励生育。适当放开计划生育政策,鼓励人们生养二胎,从根本上增加劳动力人口数量,本质上的提高人口自然增长率,解决老龄化问题。另外一个方面,需要大力发展经济,通过经济的增长抵消人口老龄化给社会发展带来的不利影响。发展老龄产业。布局老龄产业,开发老年人产品市场,既满足了老年人的需求,同时可以更好地为老年人服务。
5时间序列
5.1平稳性检验
为了验证时间序列的平稳性,可以使用单位根检验(Unit Root Test)。在这里,我们使用了Augmented Dickey-Fuller(ADF)检验来检验时间序列数据的平稳性。
根据所进行的单位根检验(ADF检验),我们对时间序列数据进行了不同差分阶数下的平稳性检验。以下是对每个差分阶数的检验结果:
表5.1 平稳性检验
差分阶数 (d) Dickey-Fuller 统计量 p-value
0 -1.7017 0.6873
1 -1.8762 0.6201
2 -3.9803 0.0235
1.差分阶数为0时,Dickey-Fuller统计量为-1.7017,p-value为0.6873。由于p-value大于通常设定的显著性水平(如0.05),我们无法拒绝原假设,即原始时间序列可能是非平稳的。
2.差分阶数为1时,Dickey-Fuller统计量为-1.8762,p-value为0.6201。同样地,p-value大于显著性水平,我们无法拒绝原假设,表明一阶差分后的时间序列可能仍然是非平稳的。
3.差分阶数为2时,Dickey-Fuller统计量为-3.9803,p-value为0.0235。在这种情况下,p-value小于显著性水平,我们可以拒绝原假设,即二阶差分后的时间序列是平稳的。
5.2 ARIMA模型
ARIMA模型是自回归移动平均模型(Autoregressive Integrated Moving Average Model)的缩写。它是一种常用的时间序列分析方法,用于对时间序列数据进行建模和预测。
根据您提供的代码,使用自动ARIMA模型拟合了二阶差分后的时间序列对象y,并得到了以下模型结果:
ARIMA(0,2,1)
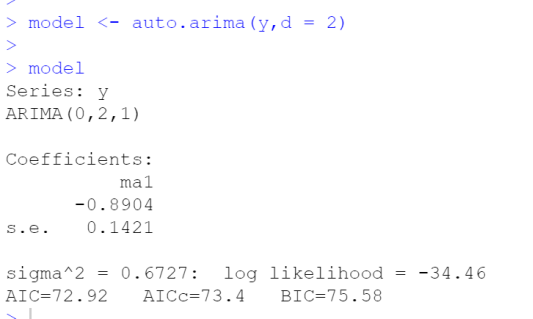
图5.1 ARIMA模型结果
模型的公司(Coefficients)如下:
ma1(滞后项1的移动平均系数):-0.8904,标准误差(s.e.)为0.1421。
其他模型的评估指标如下:
1.sigma^2(模型的方差估计):0.6727
2.对数似然值(log likelihood):-34.46
3.AIC(赤池信息准则):72.92
4.AICc(经过校正的赤池信息准则):73.4
5.BIC(贝叶斯信息准则):75.58
综合这些指标,我们可以看出模型的AR部分为0,差分阶数为2,MA部分为1。这意味着模型是一个二阶差分的移动平均模型。模型的参数估计结果显示滞后项1的移动平均系数(ma1)为-0.8904。
对模型进行了准确度评估和残差的Ljung-Box检验。以下是对结果的解释:
X-squared(卡方统计量):1.0297
p-value(p值):0.3102
Ljung-Box检验用于检查残差序列中是否存在自相关性。在这里,p-value为0.3102,大于通常设定的显著性水平(如0.05),表明残差序列可能是独立的,没有显著的自相关性。
这意味着模型的残差序列在时间上是随机分布的,没有留下未被模型捕捉的系统性模式。因此,该ARIMA模型的残差序列表现良好,符合模型假设。
通过使用ARIMA模型对时间序列进行预测,我们得到了未来一段时间的预测结果。使用plot函数将预测结果可视化展示出来。该图形显示了预测值及其相应的置信区间。

图5.2 ARIMA模型预测图
6结论和建议
本文从国家统计局官网中国统计年鉴中整理出了1990-2019年的老龄化及其相关指标数据, 分析和建模分析以人口老龄化的影响因素,笔者选取了我国人口自然增长率,国民总收入,居民消费支出和公共预算收入增长率共四个指标进行多元回归分析,其中显著性的因素分别有自然增长率 和国民总收入。
通过对人口自然增长率的时间序列分析,使用了差分阶数(d)为2的自回归移动平均模型(ARIMA(0,2,1))。最后,对模型的残差进行了Ljung-Box检验,结果显示p值为0.3102。根据Ljung-Box检验的结果,残差序列可能是独立的,没有显著的自相关性,时间序列结果拟合非常的好。
由于人口老龄化的影响因素有很多,因此再未来的研究中可以考虑在模型中加 入更多因素, 比如就业率,物价指数,自然灾害,经济贸易等等。另外,若要将模型推广到 东西部,还要进一步考虑东西部特有因素(如:在城市是否为发达等),因此本文的分析不能以偏概全。
























 2097
2097

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










