工程力学(16)—弯曲应力

一：梁弯曲的正应力

1：纯弯曲：只有弯矩没有剪力

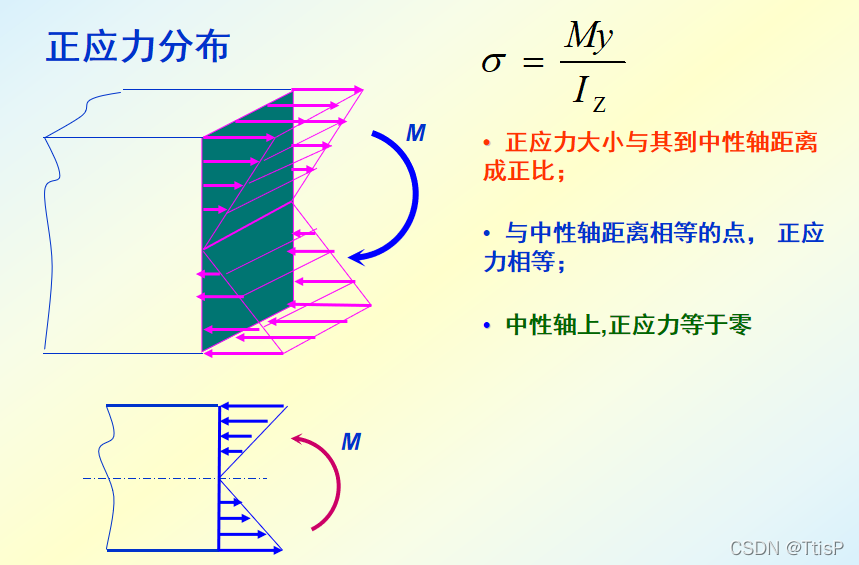
2：纯弯曲时的正应力

平面假设：横截面变形后保持为平面，且仍然垂直于变形后的梁轴线，只是绕截面内某一轴线偏转了一个角度。

做一个小小的比较：

拉伸和压缩：平面假设—变形前原为平面的横截面，变形后仍保持为平面且仍垂直于轴线。

圆轴扭转：平面假设变形前原为平面的横截面，变形后仍保持为平面，形状和大小不变，半径仍保持为直线；且相邻两截面间的距离不变。

变形几何关系

弯曲前：oo=aa=bb=dx

物理关系

静力学关系：纯弯曲，没有剪力

微元上的内力构成空间平行力系，合成的结果有Fn,My和Mz三项，但外力只有Me,所以Fn和My要为零。

对Y轴的力偶矩为0，Fn为0。
从式子Sz=0，可知：中性轴过形心
（原本只知道中性轴存在，但是不知道中性轴在那个位置，通过这样的计算我们知道中性轴是形心的。）

综上：

从这个式子可得

二：梁弯曲的强度计算

例题：

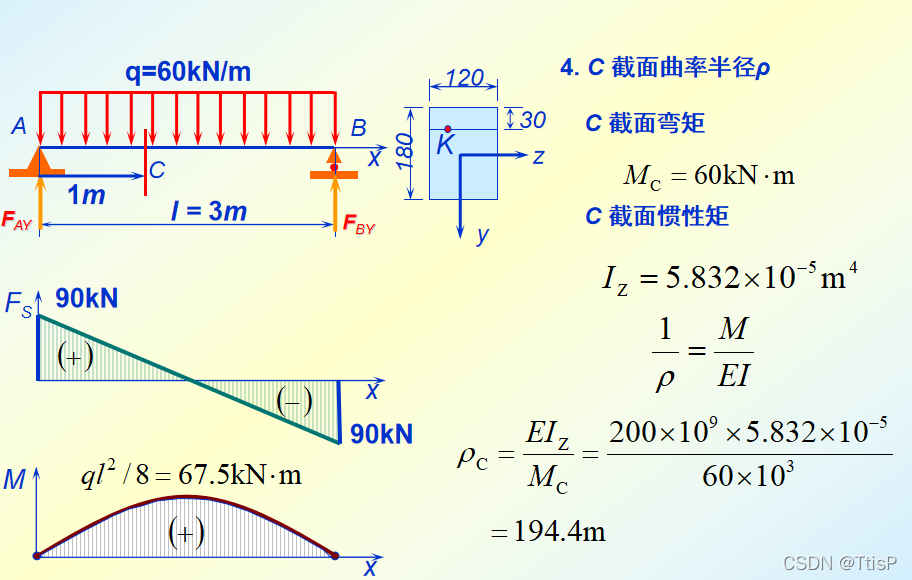
先画剪矩图，弯矩图
求得是C截面处的正应力，根据公式所需条件，先算出C截面处的M，所以在这之前得算出两个约束力的大小，再算出对Z轴的惯性矩，算出k到Z轴的距离，代入公式求解最大正应力。

C截面的力偶矩找到距离最大的位置，代入公式即可。

全梁上：找出力偶矩最大的位置

例题：

C截面校核一下拉的强度极限就OK，因为对应的ρ增大了。