工程力学(14)—弯曲内力

一：受弯杆件的简化

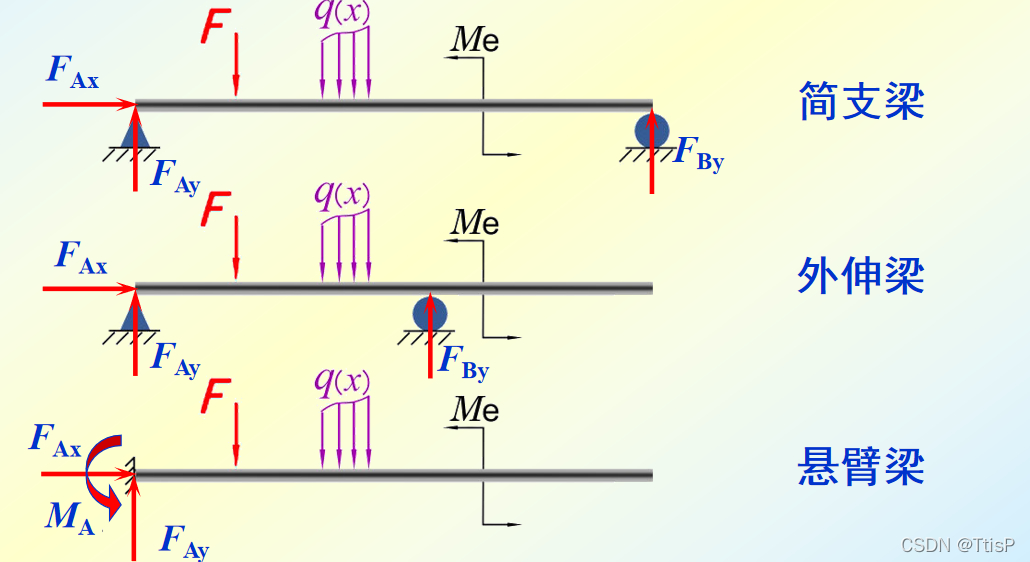
静定梁：简支梁，外伸梁，悬臂梁

简支梁，即指梁的两端搁置在支座上
外伸梁：梁一端或两端伸出支座之外
悬臂梁：梁的一端为不产生轴向、垂直位移和转动的固定支座，另一端为自由端。

二：剪力和弯矩

1：定义

剪力：平行于横截面的内里合力
弯矩：垂直于横截面内力系的合力偶矩

2：方向的判断

对于剪力：左上右下为正。（对所选梁段上任意一点的矩为顺时针转向）

对于弯矩：即左顺右逆为正。(使得梁向下凹为正)

for example:

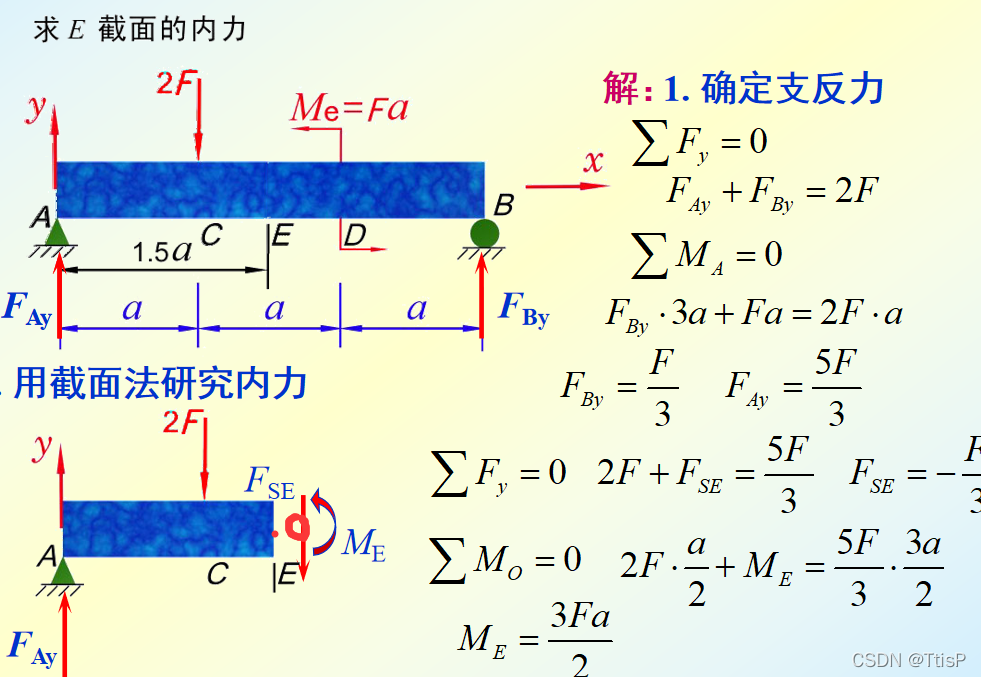
首先利用空间任意力平衡的条件列出方程：解出各个力的大小，然后通过截面法进行分析，判断方向即可。
注意：比如对于左半部分，因为剪力的正方向左上右下，所以假设剪力的方向向下，得到上图方程，当然也可以利用三平行力平衡算出，右侧剪力的大小，然后根据他的方向判断正负号。
弯矩的方程也是如此，先假设要求弯矩的截面，弯矩为正，列出方程，得出结果

左右截面得出的结果必定相同。

三：剪力方程和弯矩方程，剪力图与弯矩图

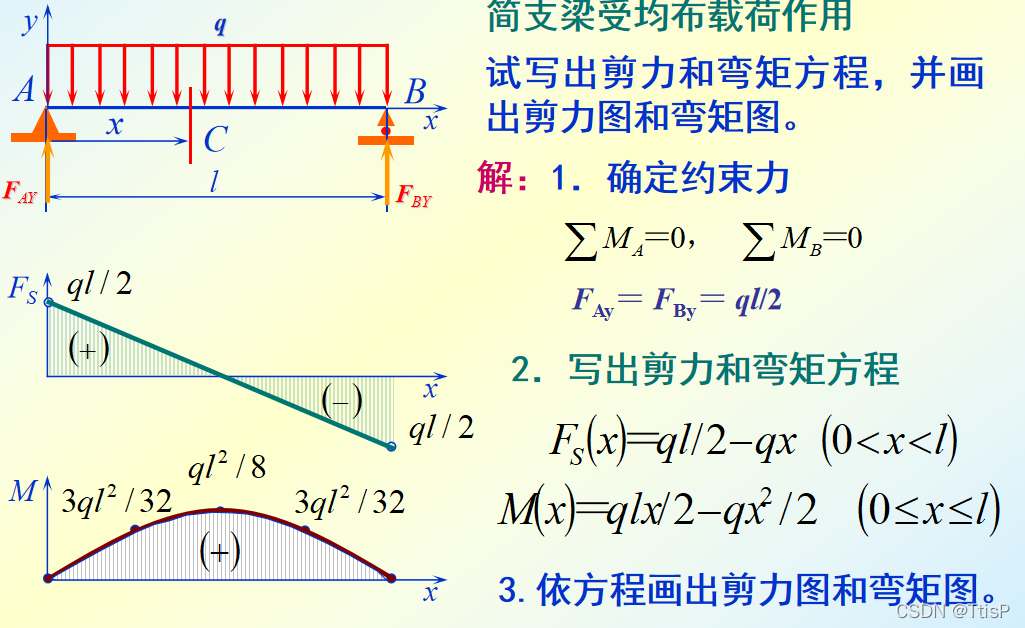
exempli gratia1：

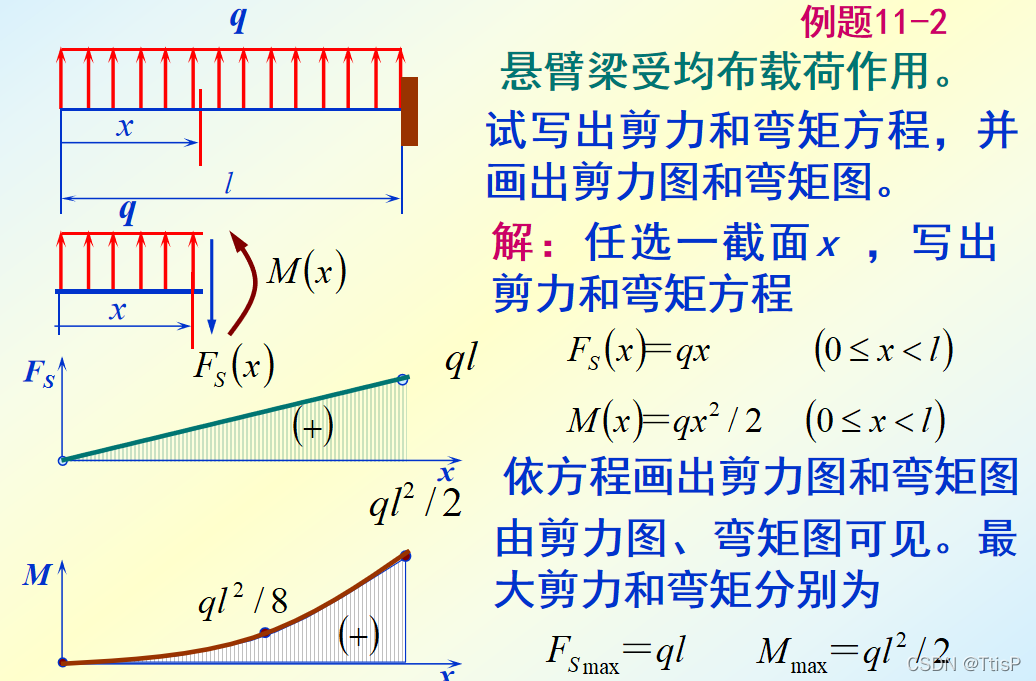
第一步：任选一截面分析剪力和弯矩
第二步推广：即可得到对应表达式子
第三：画图，得到剪力图和弯矩图

注：显而易见，弯矩方程的求导等于剪力方程（很重要）

exempli gratia2：

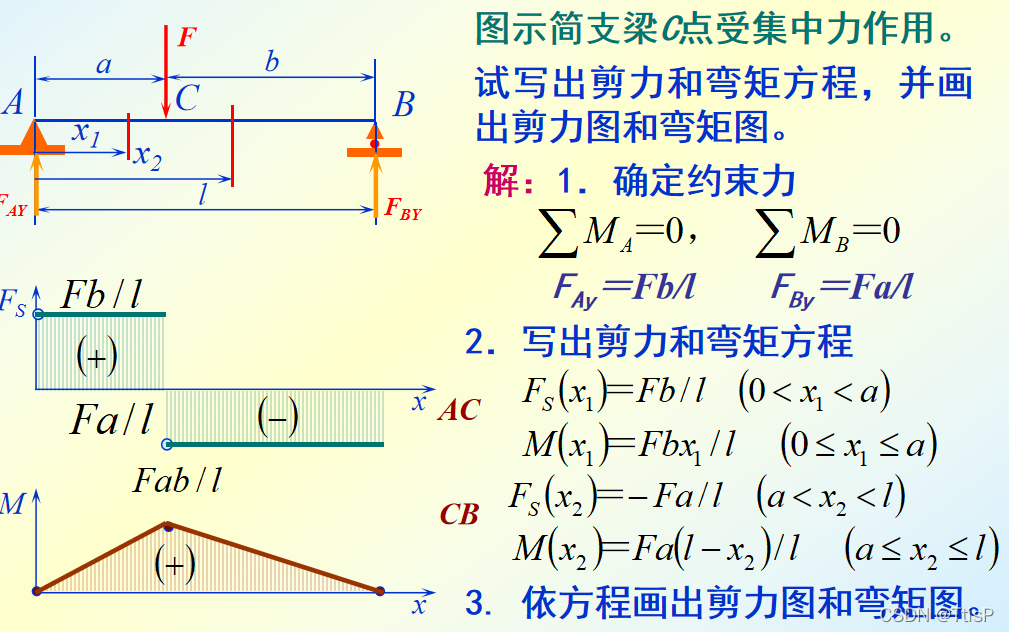
第一步：利用平衡方程确定约束力
第二步：分段表示他的剪力与弯矩
第三步：画出图像，标明极值
（应力集中的位置，弯矩图不发生突变）

exempli gratia3：

同样的
第一步：利用平衡方程确定约束力
第二步：分段表示他的剪力与弯矩
第三步：画出图像，标明极值
（力偶的作用不改变剪力图像，弯矩图像此时发生突变，力偶为顺时针时增大，逆时针时减小。同样的我们可以知道，弯矩方程的导数就是剪力方程。通过对剪力方程积分得到通解，利用截面分析某点的弯矩大小代入这一点的数值，得到弯矩方程）

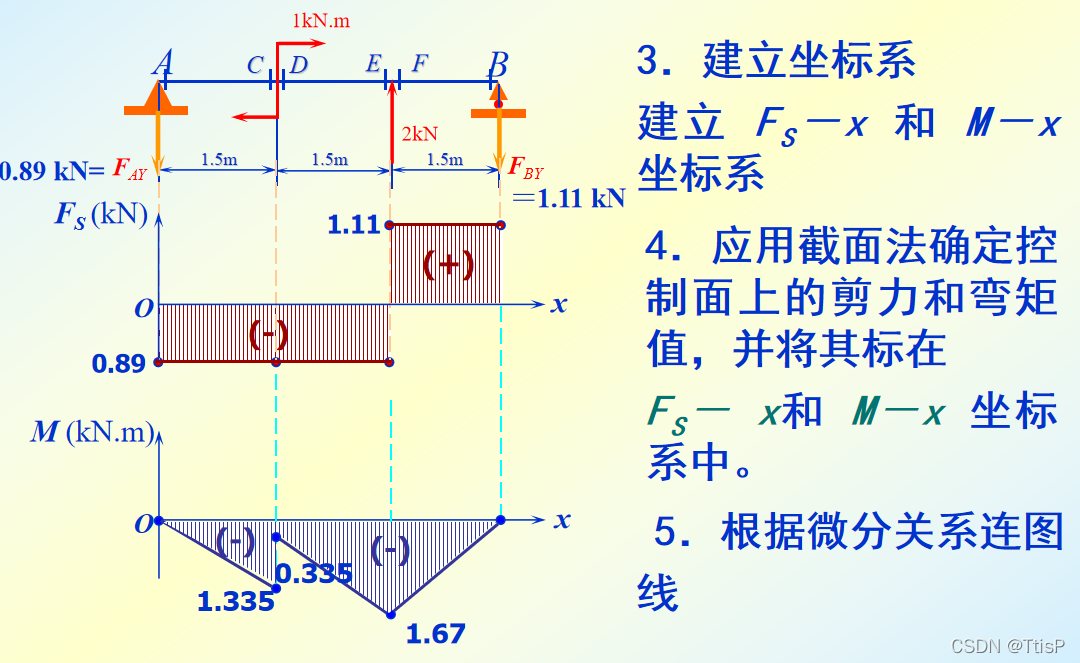
exempli gratia4：

同样的
第一步：利用平衡方程确定约束力
第二步：表示他的剪力与弯矩
第三步：画出图像，标明极值
通过对剪力方程积分得到通解，利用截面分析某点的弯矩大小代入这一点的数值，得到弯矩方程

总结：

1：剪力方程是弯矩方程的导数
2：集中力只会造成剪力图的突变。
3：力偶不会改变剪力图，只会改变弯矩图，且对弯矩图产生突变。

例题：

例题：

注意：Fay，Fby不是截面上剪力的方向

例题：