LCL滤波器电容阻尼选择

LCL滤波器的传递函数：

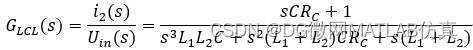
没有加入阻尼时，系统的开环极点位于S平面的虚轴上，系统处于临界稳定状态，稍有波动就会使得系统变成不稳定状态；加入阻尼电阻RC后，系统的极点移向s平面的左边，系统处于稳定状态RC通常取一个谐振频率下与电容阻抗的二分之一。

 

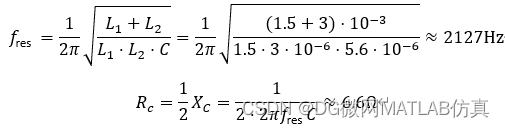
 此处取Rc=5Ω

首先忽略Rc ，LCL滤波器传递函数波特图为：  

 

 取Rc=5Ω

 

 在高频段，由于电容的容抗很小，串联电阻会增大电容支路的阻抗，从而LCL滤波器的高频谐波衰减能力有所削弱；在低频段，由于电容的容抗远大于串联电阻的阻值，串联电阻可以忽略，因此对LCL滤波器的低频段增益几乎没有影响。无源阻尼法简单可靠，能够很好抑制谐振尖峰，且不需要改变原系统的控制结构，减少控制难度，因此在工业界得到了广泛的应用。

int main()
{
    double  x, y, a;
    for (y = 1.5; y > -1.5; y -= 0.1)
    {
        for (x = -1.5; x < 1.5; x += 0.05)
        {
            a = x * x + y * y - 1;
            char ch = a * a * a - x * x * y * y*y <= 0.0 ? '*' : ' ';
            putchar(ch);
        }
        system("color 0c");   //修改颜色
        printf("\n");
    }
    printf("感谢");
    return 0;
}