【LLM 论文】Least-to-Most Prompting 让 LLM 实现复杂推理

论文：Least-to-Most Prompting Enables Complex Reasoning in Large Language Models
⭐⭐⭐
Google Research, ICLR 2023

论文速读

Chain-of-Thought（CoT） prompting 的方法通过结合 few-show prompt 的思路，让 LLM 能够挑战更具复杂性的问题。但是 CoT 的方法存在一个关键限制：它在需要泛化性来解决比 demonstration examples 更困难的问题的 task 上，通常表现不佳。

为了克服这个缺点，本论文提出了 least-to-most prompting 的方法，它先让 LLM 将原来的问题分解为多个需要预先解决的 sub-questions，然后依次按顺序让 LLM 去解决这些 sub-questions，在解决每个 sub-question 的时候，LLM 可以看到之前的每个 sub-question 以及回复。如下图：

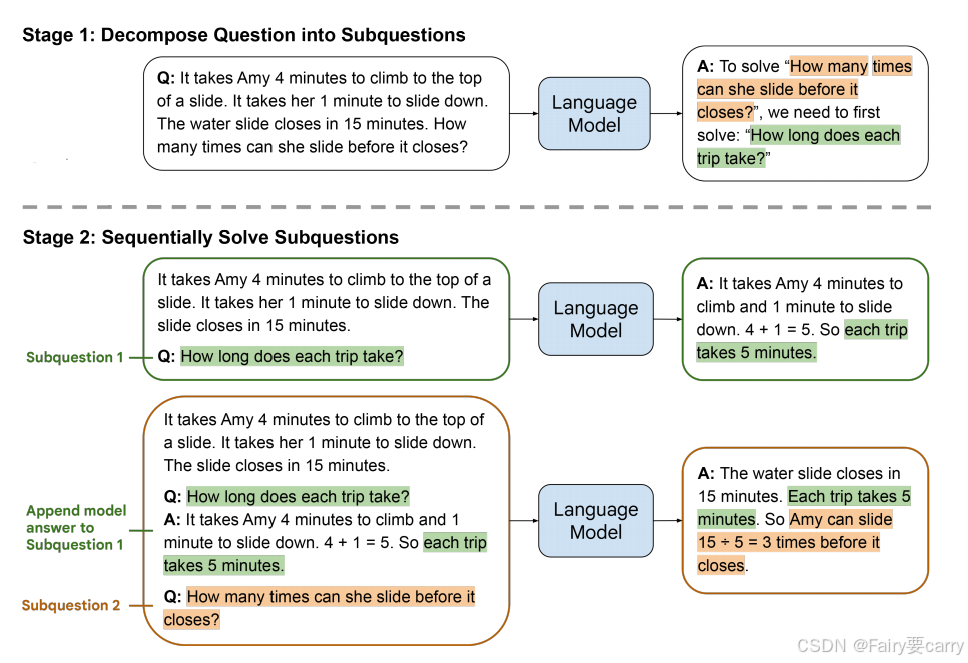
可以看到，它包含两个 stage，每个 stage 都是通过 few-shot prompt 来实现的，并且整个过程没有任何 model 被训练：

阶段 1: 问题分解（Decomposition）

• 在这个阶段，目标是将一个复杂的问题分解成几个更小、更易于解决的子问题。这个过程通常通过提供几个示例来演示如何将问题分解。例如，如果问题是“Amy 可以在滑水道关闭前滑几次？”这个问题可以被分解为两个子问题：

每次上滑和下滑的总时间是多少？
滑水道关闭前有多少时间？

• 在提供的示例中，问题被分解为第一个子问题：“每次来回需要多长时间？”通过计算上滑和下滑的时间（4分钟上滑 + 1分钟下滑 = 5分钟），我们得到了每次来回所需的时间。

阶段 2: 子问题解决（Subproblem solving）:

• 在这个阶段，目标是使用已经解决的子问题的答案来解决原始问题。这个过程包括以下几个部分：

• 示例：提供几个已经解决的子问题和答案的示例，以展示如何解决类似的子问题。【用于演示子问题如何被解决的 few-shot examplers】
  已知子问题和答案：展示之前已经回答的子问题及其答案，例如，每次来回需要5分钟。
  原始问题：然后，使用这些已知的子问题的答案来解决原始问题。在这个例子中，我们知道滑水道将在15分钟后关闭，而每次来回需要5分钟，所以Amy可以在滑水道关闭前滑3次（15分钟 / 5分钟/次 = 3次）。

实验

论文做了 symbolic manipulation、compositional generalization 和 math reasoning tasks 三个实验，并主要与 CoT 进行了对比。

总的来说，本文提出的 Least-to-Most Prompting 相比于 CoT 的优势主要在于：

在长度泛化方面更好。面对比 few-shot exemplars 更长的问题，比 CoT 解决地更好
在困难泛化方面更好。面对比 few-shot exemplars 更困难的问题，也比 CoT 解决地更好

总结与分析

论文指出，该方法的 decomposition prompt 不能很好地跨域泛化，在一个 domain 上 decomposition 的示例无法有效地用在另一个 domain（task）上。

总的来说，本工作提出了 least-to-most prompting 的方法，通过自顶向下的问题分解和自底向上的子问题解决实现了最终的解决问题。在该方法中，prompt 由以前的单向与 LLM 交流变成了双向的互动。通过双向交互来指导 LLM 仍然值得探索。
pt 由以前的单向与 LLM 交流变成了双向的互动。通过双向交互来指导 LLM 仍然值得探索。