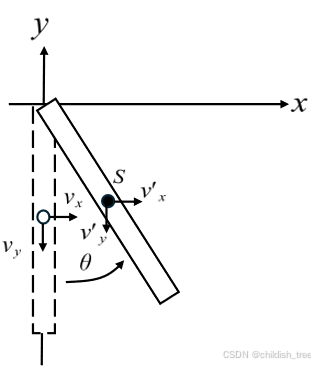
一、动力学建模
1.1 动力学公式推导过程


1.2 Matlab数值仿真
涉及单摆的动力学建模,PD控制器的设计等。
PenMain.m(主程序)
%% PenMain.m
% 单摆系统动力学仿真与PD控制
% 作者: childish_tree
% 日期: 2025/03/30
% 功能:
% 1. 求解单摆动力学方程
% 2. 生成摆杆运动动画
% 3. 绘制角度和角速度曲线
% 4. 验证动能计算等效性
close all;
clear; clc;
%% 参数设置
% 单位: kg (质量), m (长度), rad (角度), s (时间)
global m l g J
m = 1; % 摆杆质量
l = 1; % 摆杆长度
g = 9.8; % 重力加速度
J = m*(l^2)/3; % 绕旋转轴的转动惯量 (均质杆)
J_mc = m*(l^2)/12; % 绕质心的转动惯量 (均质杆)
% 仿真时间设置
stopTime = 5; % 总仿真时间
tspan = [0, stopTime]; % 时间区间
x0 = [0; 0]; % 初始状态 [theta; dtheta]
% ODE求解器选项
options = odeset('AbsTol', 1e-6, 'InitialStep', 1e-7); % 提高数值精度
%% 求解动力学方程
% 使用ode45求解微分方程,调用myDyn.m计算角加速度
[t, x] = ode45(@myDyn, tspan, x0, options);
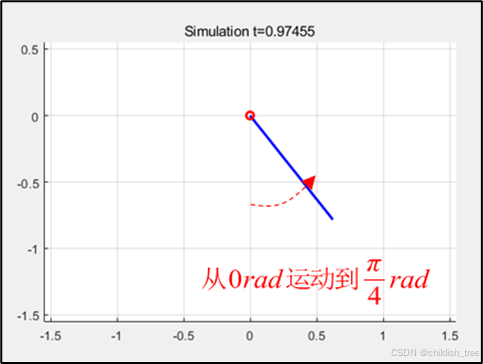
%% 生成动画
figure(1);
set(gca, 'nextplot', 'replacechildren'); % 避免内存累积
v = VideoWriter('Pen.avi'); % 创建视频文件
open(v);
x0 = 0; y0 = 0; % 旋转轴坐标(原点)
j = 1; % 动画帧索引
% 每隔200步绘制一帧动画(减少计算量)
for k = 1:200:length(t)
% 计算摆杆端点坐标
x1(j) = l*sin(x(k, 1)); % x = l*sin(theta)
y1(j) = -l*cos(x(k, 1)); % y = -l*cos(theta)(y轴向下为负)
% 绘制摆杆
link1_x = [x0, x1(j)];
link1_y = [y0, y1(j)];
line(link1_x, link1_y, 'linewidth', 2, 'color', 'b'); % 摆杆线条
% 设置坐标系显示范围
axis equal;
axis([-1.55 1.55 -1.55 0.55]); % 固定坐标范围
title(['Simulation t=', num2str(t(k))]);
grid on;
hold on;
% 绘制旋转轴(红色圆点)
plot(x0, y0, 'o', 'linewidth', 2, 'color', 'r');
% 捕获当前帧并写入视频
frame = getframe(gcf);
writeVideo(v, frame);
clf; % 清空当前图形,准备下一帧
j = j + 1;
end
close(v); % 关闭视频文件
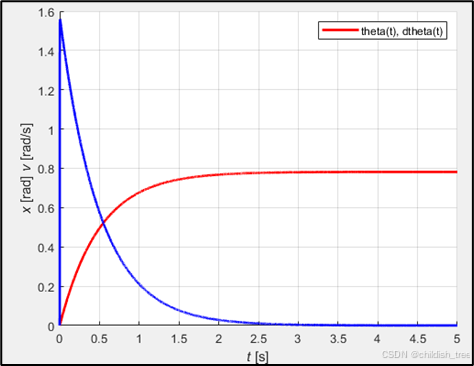
%% 绘制状态量随时间变化曲线
figure(2);
grid on; hold on;
plot(t, x(:,1), 'r-', 'linewidth', 2); % 角度曲线(红色)
plot(t, x(:,2), 'b-', 'linewidth', 2); % 角速度曲线(蓝色)
xlabel('{\itt} [s]');
ylabel('{\itx} [rad] {\itv} [rad/s]');
legend('theta(t)', 'dtheta(t)');
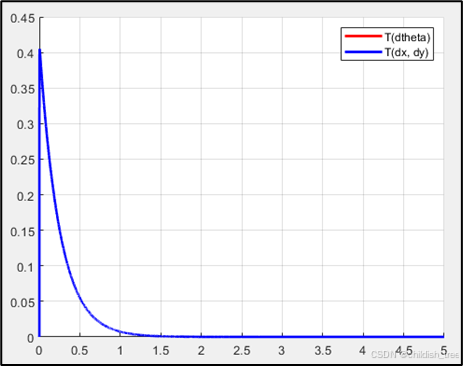
%% 动能等效性验证
figure(3);
grid on; hold on;
% 动能计算方式1: 绕旋转轴的转动动能
T1 = 0.5*J*x(:,2).^2;
% 动能计算方式2: 平移动能 + 绕质心的转动动能
dx = 0.5*l*cos(x(:,1)).*x(:,2); % 质心x方向速度
dy = 0.5*l*sin(x(:,1)).*x(:,2); % 质心y方向速度(修正后的正确符号)
T2 = 0.5*m*(dx.^2 + dy.^2) + 0.5*J_mc*x(:,2).^2;
% 绘制动能曲线
plot(t, T1, 'r-', 'linewidth', 2);
plot(t, T2, 'b-', 'linewidth', 2);
legend('T(dtheta)', 'T(dx, dy)');
title('动能等效性验证');
myDyn.m(动力学方程)
%% myDyn.m
% 单摆动力学方程计算
% 输入:
% t: 当前时间 (未直接使用)
% x: 当前状态向量 [theta; dtheta]
% 输出:
% dx: 状态导数向量 [dtheta; ddtheta]
% 公式:
% ddtheta = 3*(tau - 0.5*m*g*l*sin(theta))/(m*l^2)
function dx = myDyn(t, x)
global m l g
% 状态变量
theta = x(1); % 当前角度
dtheta = x(2); % 当前角速度
% 调用PD控制器计算控制力矩
tau = PIDController(t, x);
% 角加速度计算(动力学方程核心)
% 公式推导: J*ddtheta = tau - tau_gravity
% 其中 J = (1/3)*m*l^2, tau_gravity = 0.5*m*g*l*sin(theta)
dd_q = 3*(tau - 0.5*m*g*l*sin(theta)) / (m*l^2);
% 构建状态导数向量
dx = [dtheta; % d(theta)/dt = dtheta
dd_q]; % d(dtheta)/dt = ddtheta
t; % 显示时间(调试用,可删除)
end
PIDController.m(PD控制器)
%% PIDController.m
% PD控制器设计(动力学反问题)
% 输入:
% t: 当前时间(未使用)
% x: 当前状态向量 [theta; dtheta]
% 输出:
% tau: 控制力矩
% 控制律:
% tau = Kp*(theta_desired - theta) + Kd*(dtheta_desired - dtheta)
% 注: 此控制器为比例-微分(PD)型,缺少积分项可能导致稳态误差
function tau = PIDController(t, x)
% 目标状态
x1_desire = pi/4; % 期望角度(π/4 rad = 45°)
x2_desire = 0; % 期望角速度(静止)
% 控制增益(需根据系统特性调整)
Kp = 1000; % 比例增益:决定对角度误差的响应强度
Kd = 500; % 微分增益:抑制振荡,增加阻尼
% PD控制律计算力矩
tau = Kp*(x1_desire - x(1)) + Kd*(x2_desire - x(2));
% 注:
% 1. 当 Kp 极大时,稳态误差可忽略但可能导致超调
% 2. 实际应用中需考虑力矩幅值限制(如 |tau| ≤ tau_max)
end
运行结果如图2、3,4所示。
二、Simscape验证
2.1 创建SolidWroks单摆模型
2.2 Simscape仿真过程
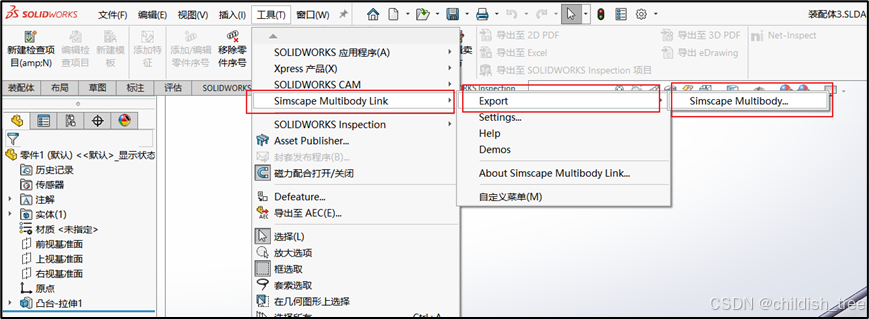
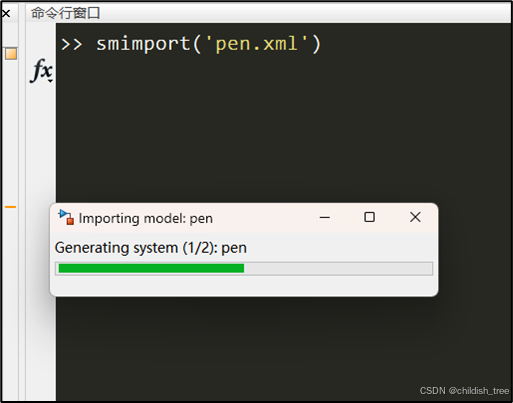
打开SW装配体模型,依次点击顶部菜单栏:工具 - Simscape Multibody Link – Export – Simscape Multibody…,导出xml格式的simcape模型。在Matlab中使用simimport(‘xxx.xml’)打开模型。具体步骤如图5,6所示。
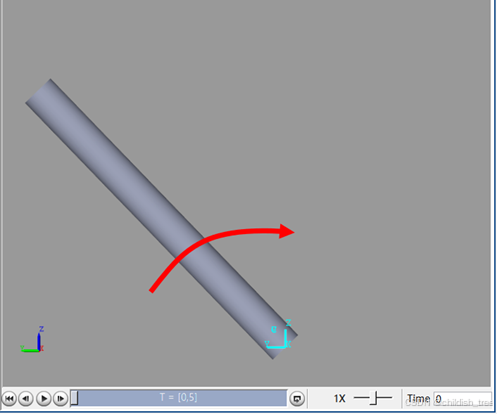
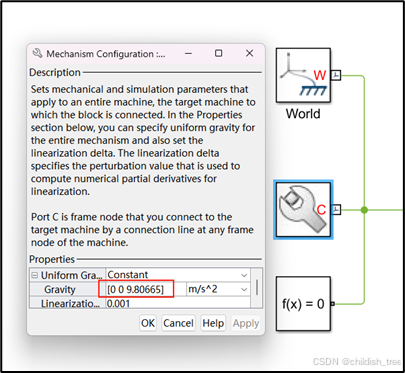
设置仿真时间(simulation stop time)为5s,初始状态杆与y轴正向呈45°。点击右下角play/pause![]() 按钮,杆在ZY全平面内运动,说明重力加速度在y轴负半轴方向。根据拉格朗日动力学建模分析知,在没加任何状态下,初始角度为45°,杆应该在ZY平面(Z>0)内运动,即重力加速度的方向应在Z轴正方向。修改Mechanism Configuration模块
按钮,杆在ZY全平面内运动,说明重力加速度在y轴负半轴方向。根据拉格朗日动力学建模分析知,在没加任何状态下,初始角度为45°,杆应该在ZY平面(Z>0)内运动,即重力加速度的方向应在Z轴正方向。修改Mechanism Configuration模块![]() 中的重力加速度参数,如下图所示。
中的重力加速度参数,如下图所示。
点击在![]() 中
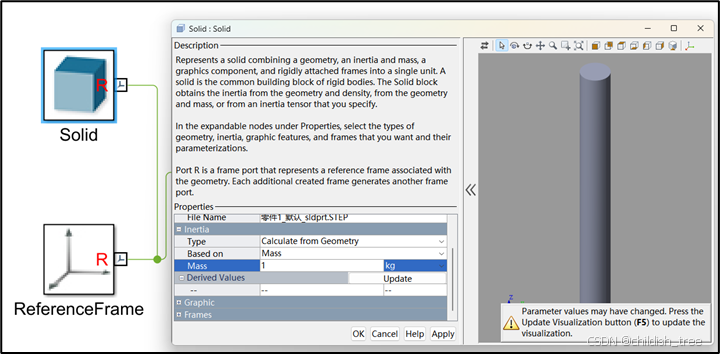
中![]() 的修改刚体属性,与拉格朗日动力学仿真匹配,如下图所示。选择从几何中计算刚体的转动惯量,手动指定刚体的质量。
的修改刚体属性,与拉格朗日动力学仿真匹配,如下图所示。选择从几何中计算刚体的转动惯量,手动指定刚体的质量。
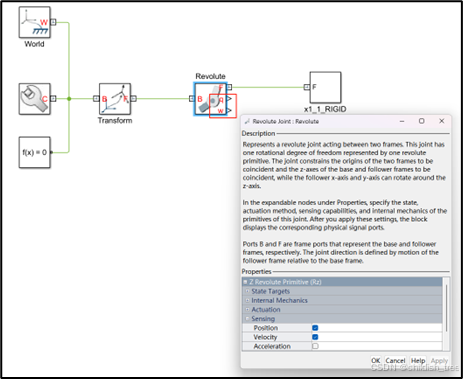
双击![]() 打开“Sensing”,选择Position和Velocity,导出角度和角速度,如下图所示。
打开“Sensing”,选择Position和Velocity,导出角度和角速度,如下图所示。
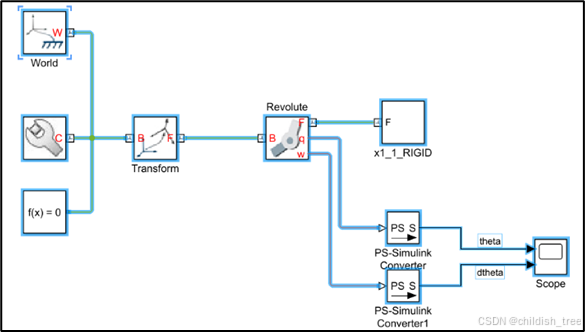
添加Scope示波器组件,并使用 PS-Simulink Converter / Simulink-PS Converter组件进行无量纲/有量纲转换,Scope组件用于显示角速度和角加速度。双击scope的输入线上添加名字,用于scope输出图像时添加图例,操作步骤如下图所示。
双击scope![]() 组件,并点击运行按钮,查看角度和角加速度关系,如下图所示。
组件,并点击运行按钮,查看角度和角加速度关系,如下图所示。
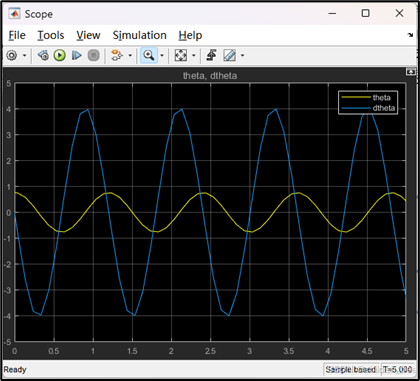
从图中可以看出,初始时,theta为pi/4,这与我们用拉格朗日动力学建模不同,使用constant模块和sum模块让theta的初始值为0,如下图所示。
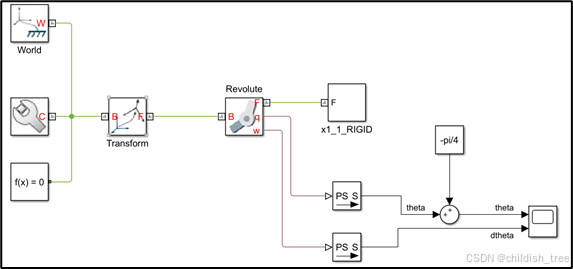
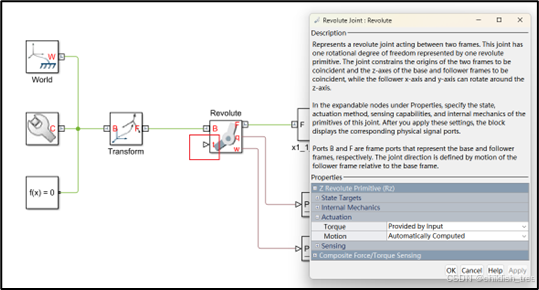
给关节Revolute ![]() 添加一个输入,采用力矩,运动采用自动计算,此目的方便建立一个具有输入输出的子系统,方便使用PID控制,如下图所示。
添加一个输入,采用力矩,运动采用自动计算,此目的方便建立一个具有输入输出的子系统,方便使用PID控制,如下图所示。
在输入的线上添加一个Simulink-PS Converter模块用于进行有量纲转换,使输入值能被子系统所使用,如下图所示。
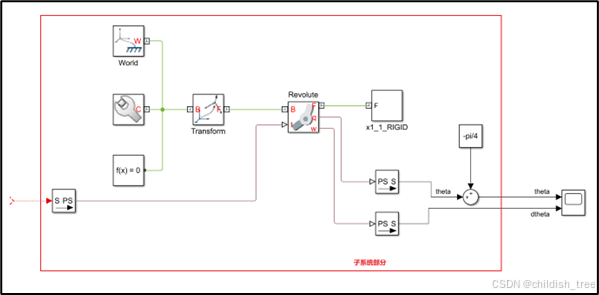
框选子系统部分,创建子系统,如下图所示。
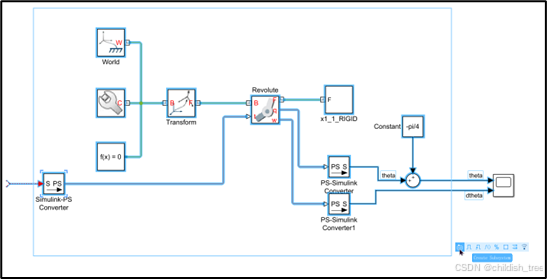
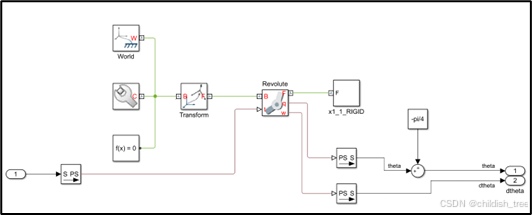
接下来,开始控制器设计,根据数值仿真中的PD设置(即PIDController.m),建立如下所示的PD控制器。
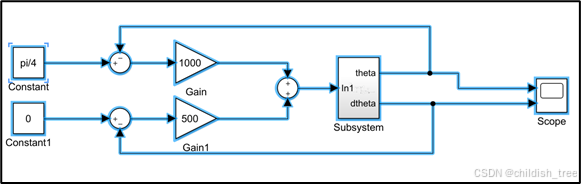
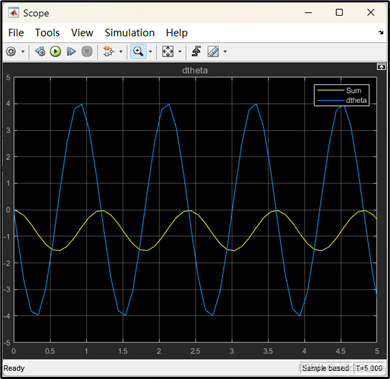
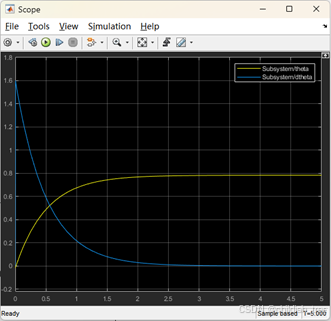
点击运行,Scope![]() 模块运行结果如下图所示,与数值仿真一致。
模块运行结果如下图所示,与数值仿真一致。
参考
matlab动力学建模与simscape验证_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1h44y1m7ca/Matlab 2018a与SolidWorks联合仿真——如何将SolidWorks模型以xml格式导出至Matlab中_matlab2018a与solidworks联合仿真-CSDN博客
https://www.bilibili.com/video/BV1h44y1m7ca/Matlab 2018a与SolidWorks联合仿真——如何将SolidWorks模型以xml格式导出至Matlab中_matlab2018a与solidworks联合仿真-CSDN博客![]() https://blog.csdn.net/BinHeon/article/details/100073149
https://blog.csdn.net/BinHeon/article/details/100073149
























 2608
2608

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










