TH方程学习（2）

最新推荐文章于 2025-05-04 08:46:09 发布

矢志航天的阿洪

最新推荐文章于 2025-05-04 08:46:09 发布

阅读量914

点赞数 5

文章标签：学习算法

本文链接：https://blog.csdn.net/weixin_57997461/article/details/139307323

版权

一、TH方程介绍

1.相对运动微分方程

首先需要介绍目标星的VVLH坐标系，以及惯性系的X,Y,Z轴的指向。Y轴指向轨道的反法向，Z轴指向目标星矢径的反方向，X轴符合右手准则。

在惯性系下，对于目标星建立微分方程可以写为

$\ddot{\boldsymbol{R}}=-\mu(\boldsymbol{R}/\left \| \boldsymbol{R} \right \|^{3})+\boldsymbol{a}_{td}$ （1）

追踪星的微分方程可以写为

$\ddot{\boldsymbol{R}}+\ddot{\boldsymbol{r}}=-\mu((\boldsymbol{R}+\boldsymbol{r})/\left \| \boldsymbol{R+r} \right \|^{3})+\boldsymbol{a}_{td}+\boldsymbol{a}_f$ （2）

其中 $\left |\boldsymbol{R+r} \right |=[\boldsymbol{(R+r)^{T}(R+r)}]^{\frac{1}{2}}=\boldsymbol{(\left | R \right |^2+2R^{T}r+\left | r \right |^2)}^{\frac{1}{2}}$

所以 $\left |\boldsymbol{R+r} \right |^{3}=\boldsymbol{\left | R \right |^{3}(1+2(R^{T}r/\left | R \right |^{2})+\left | r \right |^2/\left | R \right |^2)}^{\frac{3}{2}}$

假设追踪星和目标星的相对距离相对于地球的距离非常小，即 $\boldsymbol{\left | R \right |}\gg \boldsymbol{\left | r \right |}$

于是

$\boldsymbol{\frac{R+r}{\left | R+r \right |^{3}}} \approx\boldsymbol{ \frac{R+r}{\left | R \right |^{3}}(1+2\frac{R^Tr}{\left |R \right |^2}+\frac{\left | r \right |^2}{\left | R \right |^2})^{-\frac{3}{2}}}\\ \approx\boldsymbol{\frac{R+r}{\left | R \right |^3}\times [1-\frac{3}{2}(2\frac{R^{T}r}{\left | R \right |^{2}}+\frac{\left | r \right |^2}{\left | R \right |^2})]}\approx \boldsymbol{\frac{1}{\left | R \right |^3}(R+r-3\frac{R^Tr}{\left | R \right |^3}R)}$ （3）

以上近似对于近距离交会是有效的。由（2）式减去（1）式得到

$\boldsymbol{\ddot{r}=-\mathit{(\mu/}\left | R \right |^{3})[r-3(R^{T}r/\left | R \right |^2)R]+a_f+a_{cd}-a_{td}}$ （4）

在目标航天器坐标系的VVLH坐标系下是方便的。这个轨道坐标系通常用于描述两个航天器之间的相对动力学。一般来说，惯性坐标系中任意矢量A的时间导数可以用相对于旋转坐标系的偏差表示为

$\frac{\textup{d}\boldsymbol{A}}{\textup{d}t}=\frac{\partial \boldsymbol{A}}{\partial t}+\boldsymbol{\omega\times A}$

上式应用两次，得到新的等式

$\boldsymbol{\ddot{r}=-\mathit{(\mu/}\left | R \right |^{3})[r-3(R^{T}r/\left | R \right |^2)R]-2(\omega \times \dot{r})-\dot{\omega\times r-\omega \times(\omega \times r)}+a_f+a_{cd}-a_{td}}$ （5）

上述等式表示在旋转坐标系下的位置和速度

在目标轨道坐标系下，其角速度向量和位置向量，表达式如下：

$\boldsymbol{\omega}=\begin{bmatrix} 0\\-\omega \\ 0 \end{bmatrix},\boldsymbol{R}=\begin{bmatrix} 0\\0 \\ -R \end{bmatrix}$

其中 $\omega$ 是目标轨道角速度的大小，R是目标地球到航天器的距离，在目标航天器坐标系下的相对位置

$\boldsymbol{r}=\begin{bmatrix} x\\y \\ z \end{bmatrix}$

根据计算

$\boldsymbol{\omega \times \dot{r}}=\begin{bmatrix} -\omega \dot{z}\\0 \\ \omega\dot{x} \end{bmatrix}$

$\boldsymbol{\dot{\omega} \times {r}}=\begin{bmatrix} -\dot{\omega} {z}\\0 \\ \dot{\omega}{x} \end{bmatrix}$

$\boldsymbol{\omega \times (\omega \times r)}=\begin{bmatrix} -\omega^{2}x\\0 \\ -\omega^{2}z \end{bmatrix}$

$\boldsymbol{r-3\frac{R^{T}r}{\left | R \right |^2}R}=\begin{bmatrix} x\\y \\ -2z \end{bmatrix}$

根据角动量的关系 $R^2\omega=h$ ，其中 $h$ 是目标航天器的角动量，我们能够定义常值k为

$\mu/R^{3}=(\mu/h^{\frac{3}{2}})\omega^{\frac{3}{2}}\equiv k\omega^{\frac{3}{2}},k\equiv\mu/h^{\frac{3}{2}}=\textup{const}$

在目标航天的轨道坐标系下，其航天器的微分方程可以写为

$\begin{bmatrix} \ddot{x}\\\ddot{y} \\ \ddot{z} \end{bmatrix}=\begin{bmatrix} -k\omega^{\frac{3}{2}}x+2\omega\dot{z}+\dot{\omega}z+\omega^{2}x\\-k\omega^{\frac{3}{2}}y \\ 2k\omega^{\frac{3}{2}}z-2\omega\dot{x}-\dot{\omega}x+\omega^{2}z \end{bmatrix}+\boldsymbol{a_f+a_{cd}-a_{td}}$ （7）

唯一的假设是，追逐者和目标之间的距离比目标和地球中心之间的距离很小，上式适用于任意偏心度的轨道。同时为了简化问题，假设

$\boldsymbol{a_f=0,a_{cd}=a_{td}}$

这个意味着追踪者是不额外添加其他外力，同时追踪星和目标星受到的摄动力是相同的。最终目的是来求解该微分方程。

2.相对运动方程的简化

为了将1中所得到的微分方程（7）简化，采用将真近地点角作为变量，而不是选择时间作为变量。形式被改写成如下形式

$\begin{bmatrix} \tilde{x}\\ \tilde{y} \\ \tilde{z} \end{bmatrix}=(1+e\cos\theta)\begin{bmatrix} x\\ y \\ z \end{bmatrix}$

因为真近点角 $\theta$ 是随着时间t单调递增，目标航天器的独立变量能够从时间t换成真近地点角 $\theta$ 。任意变量a与时间相关的导数变为

$\frac{\textup{d}a}{\textup{d}t}=\frac{\textup{d}a}{\textup{d}\theta}\frac{\textup{d}\theta}{\textup{d}t}=\omega\frac{\textup{d}a}{\textup{d}\theta}$

二次求导

$\frac{\textup{d}^2a}{\textup{d}t^2}=\frac{\textup{d}}{\textup{d}t}(\frac{\textup{d}a}{\textup{d}t})=\omega \frac{\textup{d}}{\textup{d}\theta}(\omega\frac{\textup{d}a}{\textup{d}\theta})=\omega(\frac{\textup{d}\omega}{\textup{d}\theta}\frac{\textup{d}a}{\textup{d}\theta}+\omega\frac{\textup{d}^{2}a}{\textup{d}\theta^2})=\omega\frac{\textup{d}\omega}{\textup{d}\theta}\frac{\textup{d}a}{\textup{d}\theta} +\omega^{2}\frac{\textup{d}^2a}{\textup{d}\theta^2}$

将关于真近地点角 $\theta$ 的导数写为如下形式

$\frac{\textup{d}a}{\textup{d}\theta}=a^{'}$

上式可以写成如下形式

$\dot{a}=\omega a^{'},\ddot{a}=\omega^{2}a^{''}+\omega \omega^{'}a^{'}$ ，将该表达式代入式（7）可以得到

$\omega^{2}x^{''}+\omega\omega^{'}x^{'}=(\omega^2-k\omega^{\frac{3}{2}})x+2\omega^{2}z^{'}+\omega\omega^{'}z\\\omega^2y^{''}+\omega\omega^{'}y^{'}=-k\omega^{\frac{3}{2}}y\\\omega^{2}z^{''}+\omega\omega^{'}z^{'}=(\omega^{2}+2k\omega^{\frac{3}{2}})z-2\omega^2x^{'}-\omega\omega^{'}x$ （8）

对于角动量，得到

$\omega=(h/R^2)=(h/p^2)(1+e\cos\theta)^2=k^2(1+e\cos\theta)^2=k^2\rho^2\\\rho \equiv 1+e\cos\theta\\\omega^{'}=2k^2\rho\rho^{'}=-2k^2e\sin\theta\rho$

因此，这个微分方程可以简化为

$\rho x^{''}-2e\sin\theta x^{'}-e\cos\theta x=2\rho z^{'}-2e \sin\theta z\\ \rho y^{''}-2e\sin\theta y^{'}=-y\\ \rho z^{''}-2e\sin\theta z^{'}-(3+e\cos\theta)z=-2\rho x^{'}+2e\sin\theta x$ （9）

根据独立变量变化的形式

$\begin{bmatrix} \tilde{x}\\ \tilde{y} \\ \tilde{z} \end{bmatrix}=\rho\begin{bmatrix} x\\ y \\ z \end{bmatrix}$

得到

$\tilde{x}^{'}=\rho x^{'}-e\sin \theta x\\\tilde{x}^{''}=\rho x^{''}-2e\sin \theta x^{'}-e\cos\theta x$

对于其他两个坐标也是同样的结果，得到相对运动方程为

$\tilde{x}^{''}=2\tilde{z}^{'}\\ \tilde{y}^{''}=-\tilde{y}\\\tilde{z}^{''}=3\tilde{z}/\rho-2\tilde{x}^{'}$ （10）

y的部分是和谐的振荡。它能被解析求出来，其结果为

$\tilde{y}=K_{y1}\sin\theta+K_{y2}\cos\theta$

对于x,z部分，等式 $\tilde{x}^{'}=2\tilde{z}+K_{x1}$ 其中 $K_{x1}$ 是积分常值

当这个等式添加到z的表达式，得到

$\tilde{z}^{''}+(4-3/\rho)\tilde{z}=-2K_{x1}$ （11）

这个问题现在简化为解决前面的微分方程 $\tilde{z}$

3.新的解析解的提出

根据作者之前写的《不含一阶导数项的线性二阶微分方程的通解》，要求解（11)式，首先需要求出其齐次项的通解，即求解

$\tilde{z}^{''}+(4-3/\rho)\tilde{z}=0$ （12）

可以求出其两个不相关的齐次线性方程解，可以写为

$\varphi_{1}=\rho \sin \theta\\\varphi_{2}=3e^{2}\sin \theta J+\rho \cos \theta -2e$ （13）

其中 $J=k^2(t-t_0)$ ，其求出的朗斯基行列式为 $\varphi_{1}\varphi_{2}^{'}-\varphi_{1}^{'}\varphi_{2}=e^2-1$

对于椭圆轨道 $0\leq e <1$ ， $e^2-1\neq 0$

因此可以证明两个解是线性独立的。当这些线性独立解被使用，式（11）的特解可以被计算得到

$\varphi_{3}=\frac{2K_{x1}}{e^2-1}(\varphi_1\int \varphi_{2}\textup{d}\theta-\varphi_{2} \int \varphi_{1}\textup{d}\theta)$ （14）

如果按照下面等式插入，

$\int \varphi_{1}\textup{d}\theta=-\frac{1}{2e}\rho^2\\\int \varphi_{2}\textup{d}\theta=-\frac{3}{2}e\rho^2J+\frac{1}{2}\sin\theta(\rho+1)$

可以得到特解

$\varphi_{3}=-(K_{x1}/e)\rho \cos \theta$ ，因此得到 $\tilde{z}=K_{z1}\varphi_{1}+K_{z2}\varphi_{2}+\varphi_{3}=\\K_{z1}\rho\sin\theta+K_{z2}(3e^2\rho \sin \theta J+\rho \cos \theta-2e)-(K_{x1}/e)\rho \cos \theta$

上式可以重新写成

$\tilde{z}=K_{z1}\rho \sin \theta +(K_{z2}-K_{x1}/e)\rho\cos\theta-K_{z2}e(2-3e\rho\sin\theta J)$

将该表达式代入x的微分方程中

$\tilde{x}^{'}=2\tilde{z}+K_{x1}=2K_{z1}\rho\sin\theta+(K_{z2}-K_{x1}/e)(2\rho\cos-e)-3K_{z2}e(1-2e\rho \sin \theta J)$

它能够被积分成

$\tilde{x}=K_{x2}-K_{z1}\cos\theta(\rho+1)+(K_{z2}-K_{x1}/e)\sin\theta(\rho+1)-3K_{z2}e\rho^{2}J$

其中 $K_{x2}$ 是一个积分常值。为了方便，我们重新定义积分常值为

$K_{1}\equiv K_{x2},K_{2}\equiv K_{z1}\\K_3 \equiv [K_{z2}-(K_{x1}/e)],K_4 \equiv -K_{z2}e$

所以最后

$\tilde{x}=K_{1}-K_{2}\cos\theta(\rho+1)+K_{3}\sin(\rho+1)+3K_{4}\rho^2J\\ \tilde{z}=K_{2}\rho\sin\theta+K_{3}\rho\cos\theta+K_{4}(2-3e\rho\sin\theta J)$

如果我们使用一种类似于CW的形式

$s=\rho \sin \theta,c=\rho \cos\theta$

所以上式又可以简写为

$\tilde{x}=K_{1}-K_{2}c(1+1/\rho)+K_3 s(1+1/\rho)+3K_4\rho^2 J\\ \tilde{z}=K_{2}s+K_3c+K_4(2-3esJ)$

将上式对 $\theta$ 求导得到

$\tilde{v}_{x}=2K_2s+K_3(2c-e)+3K_4(1-2esJ)\\ \tilde{v}_{z}=K_{2}s^{'}+K_3c^{'}-3K_4e(s^{'}J+s/\rho^2)$

如果表达成平面内的形式，这个不等式可以写为

其中

$s^{'}=\cos \theta+e\cos2\theta,c^{'}=-(\sin\theta+e\sin2\theta)\\ J=k^2(t-t_0),k^2=h/p^2$

我们需要的状态转移矩阵，可以在任意时刻将初始状态传播到最终状态位置，这个不等式能够获得通过插入初始状态求出K值，根据上面获得的式子得到了 $\boldsymbol{\Phi}_{\theta}$ ，根据J的关系

$J(\theta_{0})=0$

所以上式可以写为

求出行列式

得到 $\det \Phi_{\theta_{0}}=e^2-1\neq0,0\leq e<1$ ，求出

所以K值即 $\boldsymbol{K}=\boldsymbol{\Phi}_{\theta_{0}}^{-1}\boldsymbol{x}_0$

其中 $\boldsymbol{x}_0=[\tilde{x}_0,\tilde{z}_0,\tilde{v}_{x0},\tilde{v}_{z0}]^{T}$ ，因此任意矩阵可以由等式求出

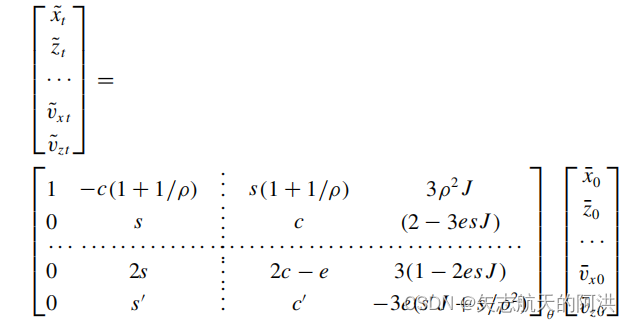
关于y轴的方向，可以由下列等式求出

最后介绍一下 $\boldsymbol{\tilde{r},\tilde{v}}$ 与 $\boldsymbol{r,v}$ 的转换关系

$\tilde{\boldsymbol{r}}=\rho \boldsymbol{r},\tilde{\boldsymbol{v}}=-e\sin\theta \boldsymbol{r}+(1/k^2\rho)\boldsymbol{v}$

$\boldsymbol{r}=1/\rho \tilde{\boldsymbol{r}},\boldsymbol{v}=k^2(e\sin\theta \tilde{\boldsymbol{r}}+\rho \tilde{\boldsymbol{v}})$

而 $\theta$ 可以通过开普勒方程求解得到。下一节将通过编程实现上述算法。