离散傅里叶变换是傅里叶变换在时域和频域都呈现离散形式的一种变换。离散时间傅里叶变换(DTFT)是将原信号在时域上离散化,是频率的连续函数,而DFT是将DTFT在频域上进行离散化。DFT是针对有限长序列的傅里叶变换,DFT本身也是一个序列,并且具有周期性,即时域和频域上的序列是有限长的。
1、DFT的定义式:
当 0 ≤ n ≤ N-1 时,有限长序列 x[n] 的 N点 离散傅里叶变换(DFT)为,
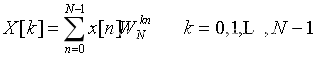
其中,有
长度为 N 的离散时间序列 x[n] 的离散傅里叶变换 X[k] 等于其离散时间傅里叶变换,
在 N 个均匀间隔频率点  所求的频率样本。即
所求的频率样本。即

2、MATLAB中离散傅里叶变换和离散傅里叶逆变换
% 离散傅里叶变换和离散傅里叶逆变换的计算
% Computation of DFT and IDFT
clear;clc;close all
x=[1 2 3 4 5 6 7 8]; % discrete-time sequence
L=length(x);
N=L; % set samples number in frequency domain
% 当采样小于 L 时会发生混叠
w=2*pi/N*(0:N-1); % discrete frequency
Xw=zeros(1,N); % vector for storing DFT
for k=1:N
Xw(k)=x*(exp(-j*w(k)*(0:L-1)')); % DFT
end
y=zeros(1,N);
for n=1:N
y(n)=(1/N)*Xw* (exp(j*(n-1)*w')); % IDFT
end
y=real(y);可以通过以上的运算过程写出一个 DFT 和 IDFT 的函数:
function [X] = dft(x,L)
% 对一个离散序列进行DFT
% x为序列长度为 L 的离散时间序列,X为DFT结果
N=L; % set samples number in frequency domain
w=2*pi/N*(0:N-1); % discrete frequency
X=zeros(1,N); % vector for storing DFT
for k=1:N
X(k)=x*(exp(-i*w(k)*(0:L-1)')); % DFT
end
endfunction [x] = idft(X,L)
% 对一个离散序列进行 IDFT
% X为序列长度为 L 的DFT序列,x为IDFT结果
N=L; % set samples number in frequency domain
w=2*pi/N*(0:N-1); % discrete frequency
x=zeros(1,N);
for n=1:N
x(n)=(1/N)*X* (exp(j*(n-1)*w')); % IDFT
end
end





















 1455
1455











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










