机器学习——多层感知器（Multi-layer Perceptrons）

一、感知器（Percetron）

1、感知器

感知器是神经网络中神经元（Neuron）的基本模型，由输入、激活函数（Activation Function）和输出构成。可用于解决回归问题，和分类问题（属于线性分类器）。

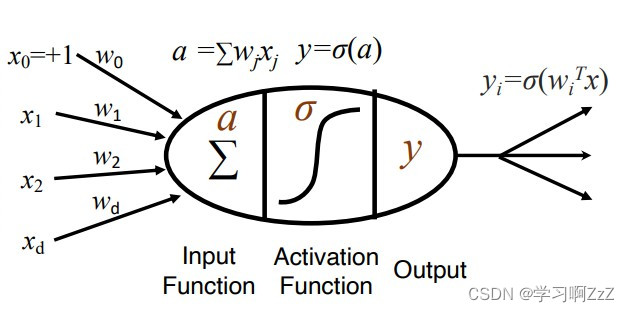
 2、感知器模型

 

 

 

其中，x为d维属性（恒为1表示偏置），w为属性对应的权重，a为属性的加权和，为激活函数，y为感知器输出。

3、感知器缺点

单层感知器只能学习线性可分数据，无法解决布尔运算中的异或问题（XOR）！

二、多层感知器（Multi-layer Perceptrons）

1、多层感知器

为解决单层感知器存在的无法学习线性不可分的问题，引入隐藏层（hidden layer(s)）。

 为解决分类问题中存在的阈值函数（thresholding function）不可微的问题，引入激活函数（activation function）。

多层感知器是一个通用估计器，可以用于估计任何非线性函数。

2、多层感知器模型

多层感知器模型即为多个单层感知器的叠加，模型如下图所示。

 模型与单层感知器类似，表示如下：

 

 

 

3、多层感知器损失函数

以L2损失函数为例

4、多层感知机优化算法

以上述两层感知器为例，使用L2损失函数，梯度下降（Gradient Descent）

 

 其中，为激活函数的导数，、分别为对应参数的梯度。

三、反向传播（Backpropagation）

1、反向传播

由于梯度下降过程中，梯度中间存在依赖，因此直接推导梯度通常是不灵活的、不可行的。

反向传播则是一种高效的计算梯度的方法。

2、反向传播过程

根据链式法则，梯度计算公式如下所示。

反向传播将梯度计算拆分为正向传递（Forward pass）和反向传递 （Backward pass）两个过程，分别计算和 。

• 正向传递（Forward pass）

 在正向传递的过程中，计算所有参数的：

•  反向传递 （Backward pass）

 在反向传递的过程中，计算所有输出a的

 

 

 可以看见计算是一个递归的过程，所以可以从输出层反向传递到输入层。

 四、多层感知器实践（PyTorch）

 以MNIST手写数字识别数据集为例

 1、数据准备

加载MINIST数据集，并将数据转换为张量（Tensor）

train_dataset = torchvision.datasets.MNIST(root='./data', train=True,
                                           transform=transform.ToTensor())  # 加载MNIST数据集，将图像转换为张量

 Hold-out，划分训练集和验证集

train_data, valid_data, train_target, valid_target = train_test_split(train_dataset.data, train_dataset.targets,
                                                                      test_size=0.33,
                                                                      random_state=23)  # 将数据集划分为训练集和验证集，验证集占比为0.33，随机种子为23

将训练集和验证集的数据和标签合并为张量数据集。

注意，在PyTorch中，神经网络层的权重通常为Float32，因此需要将数据转换为float。

train_dataset = TensorDataset(train_data.float(), train_target)  # 将训练集的数据和标签封装为张量数据集
valid_dataset = TensorDataset(valid_data.float(), valid_target)  # 将验证集的数据和标签封装为张量数据集

 分别加载训练集和验证集

BATCH_SIZE = 256
train_dataloader = DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True)  # 创建训练集的数据加载器，打乱顺序
valid_dataloader = DataLoader(dataset=valid_dataset, batch_size=BATCH_SIZE, shuffle=False)  # 创建验证集的数据加载器，不打乱顺序

2、训练模型

编写设备无关代码，根据是否有可用GPU，选择是否使用cuda加速。

device = "cuda" if torch.cuda.is_available() else "cpu"  # 判断是否有可用的GPU，如果有则使用，否则使用CPU

 定义一个MLP类，定义为两层感知机(即隐藏层+输出层)，每层为一个线性层+Sigmoid激活函数。

# 定义一个多层感知机类
class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()  # 调用父类的初始化方法
        self.model = nn.Sequential(
            nn.Linear(in_features=28 * 28, out_features=10 * 10, bias=True),  # 一个线性层，输入特征为28*28（图像大小），输出特征为10*10，有偏置项
            nn.Sigmoid(),  # Sigmoid激活函数
            nn.Linear(in_features=10 * 10, out_features=10, bias=True),  # 一个线性层，输入特征为10*10，输出特征为10（类别数），有偏置项
            nn.Sigmoid()  # Sigmoid激活函数
        )

MLP类的前向传播方法。由于线性层只改变最后一个维度，一般输入二维矩阵，因此将数据修改为（batch_size,data）的形式。

    def forward(self, data):
        data = data.view(data.size(0), -1)  # 将数据展平为一维向量，保留第一维（批量大小）
        return self.model(data)

创建模型、优化器和损失函数。

model = MLP().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)  # 创建一个Adam优化器，学习率为0.001
lossFn = nn.CrossEntropyLoss()  # 创建一个交叉熵损失函数

 训练模型

EPOCH = 500
train_loss_epoch = []  # 存储每个epoch的平均损失
valid_loss_epoch = []  # 存储每个epoch的平均损失
for epoch in range(EPOCH):
    print("Epoch : {}".format(epoch))
    model.train()  # 将模型设置为训练模式

    train_loss_batch = []  # 存储每个batch的损失
    for images, labels in train_dataloader:
        images = images.to(device)
        labels = labels.to(device)

        optimizer.zero_grad()  # 将优化器的梯度清零

        outputs = model(images)  # 将图像输入模型，得到输出
        loss = lossFn(outputs, labels)  # 计算输出和标签之间的损失
        loss.backward()  # 反向传播，计算梯度
        optimizer.step()  # 更新参数

        train_loss_batch.append(loss.item())
    mean_train_loss = np.mean(train_loss_batch)  # 计算epoch的平均损失
    train_loss_epoch.append(mean_train_loss)
    print("Loss of train-set : {:.4f}".format(mean_train_loss))

    model.eval()  # 将模型设置为评估模式

    valid_loss_batch = []  # 存储每个batch的损失
    with torch.no_grad():  # 不计算梯度
        for images, labels in valid_dataloader:
            images = images.to(device)
            labels = labels.to(device)

            outputs = model(images)  # 将图像输入模型，得到输出
            loss = lossFn(outputs, labels)  # 计算输出和标签之间的损失

            valid_loss_batch.append(loss.item())
    mean_valid_loss = np.mean(valid_loss_batch)  # 计算每轮验证的平均损失
    valid_loss_epoch.append(mean_valid_loss)
    print("Loss of valid-set : {:.4f}".format(mean_valid_loss))

可视化训练过程中损失函数的变化

plt.plot(np.arange(EPOCH), train_loss_epoch, label='Train loss')
plt.plot(np.arange(EPOCH), valid_loss_epoch, label='Valid loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.savefig('./fig/loss_' + str(EPOCH) + '.png')
plt.clf()

结果如下：

 保存模型

torch.save(model, './model/model_' + str(EPOCH) + '.pth')  # 保存模型到文件中

3、评估模型

同训练集和验证集，先准备测试集数据

test_dataset = torchvision.datasets.MNIST(root='./data', train=False,
                                          transform=transform.ToTensor())  # 加载MNIST数据集，将图像转换为张量

test_dataset = TensorDataset(test_dataset.data.float(), test_dataset.targets)

BATCH_SIZE = 256
test_dataloader = DataLoader(dataset=test_dataset, batch_size=BATCH_SIZE, shuffle=False)  # 创建测试集的数据加载器，不打乱顺序

 加载模型

model = torch.load('./model/model_500.pth')  # 加载训练好的模型

测试模型。预测值根据模型输出得分计算max()得到，max()输出结果为（max_data，index）的形式。

model.eval()  # 将模型设置为评估模式
test_predicts = torch.LongTensor()  # 存储预测结果
test_predicts = test_predicts.to(device)
test_labels = torch.LongTensor()  # 存储真实标签
test_labels = test_labels.to(device)
with torch.no_grad():  # 不计算梯度
    for images, labels in test_dataloader:
        images = images.to(device)
        labels = labels.to(device)

        outputs = model(images)
        predicts = outputs.max(1, keepdim=True)[1]  # 得到每个输出的最大值的索引，即预测的类别
        test_predicts = torch.cat((test_predicts, predicts), dim=0)  # 将预测结果拼接到张量中
        test_labels = torch.cat((test_labels, labels), dim=0)  # 将真实标签拼接到张量中

计算模型在测试集上准确率

test_predicts = test_predicts.view(test_predicts.size(0))  # 将预测结果展平为一维向量
accuracy = (test_predicts == test_labels).sum().item() / test_labels.size(0)  # 计算预测结果和真实标签的一致性，即准确率
print("Accuracy of test-set : {:.4f}".format(accuracy))

结果如下：

Accuracy of test-set : 0.9620

 使用混淆矩阵（confusion-matrix）评估模型。

print(pd.crosstab(test_labels.to('cpu').numpy(), test_predicts.to('cpu').numpy(), rownames=['Predict Value'],
                  colnames=['True Value']))  # 打印混淆矩阵，显示每个类别的预测和真实值的对应关系

 结果如下：

True Value	0	1	2	3	4	5	6	7	8	9
Predict Value
0	965	0	1	2	2	1	6	2	1	0
1	0	1121	3	2	0	0	2	1	6	0
2	5	0	998	6	4	0	1	6	12	0
3	0	0	6	997	2	6	1	7	7	4
4	2	0	1	0	952	0	7	3	1	16
5	2	1	0	25	1	843	6	1	10	3
6	9	3	4	2	7	7	922	0	4	0
7	1	8	17	3	3	0	0	985	1	10
8	9	1	5	13	6	8	5	5	917	5
9	8	7	1	8	26	3	1	11	4	940

(完整源代码见"MLP识别MNIST手写数字数据集(Pytorch)")